- 1PyTorch--线性回归_pytorch之线性回归头歌
- 2hadoop各组件工作流程分析
- 3Hello, GPT-4o!
- 4Windows下rsync软件配置和使用_window rsync设置全局变量
- 5跨领域知识迁移学习在提升大模型泛化能力中的应用_不同领域的大模型迁移
- 6Window环境下apache配置的Django静态文件如css、js不显示问题解决_django读取网页静态资源js不显示
- 7Python面试常见问题,涉及Python各个方面_tkinter项目毕业答辩可能问的问题
- 8测试工程师经验(一)_input overload测试
- 9navicat for mysql 定时计划 定时导出EXCEL并附件发送邮件到固定邮箱_在线文档定时导出
- 10clickhouse hbase性能对比_为什么我们要从ES迁移到ClickHouse?
数据结构和算法学习(3)- 递归、回溯_cure算法所用的数据结构
赞
踩
递归是什么?
递归就是循坏,通过函数来进行循环,类比盗梦空间:
- 向下进入不同的梦境中,向上又回到原来一层(递归只能一层层向下/向上,不能跳过其中某一层)
- 通过声音同步回到上一层(函数不同层之间传递变量)
- 每一层环境和周围的人都是一份拷贝,主角等几个人穿越不同层的梦境(参数和携带变化)
计算 n 递归的简单例子
!n = 1*2*3…*n
public int factorial(){
if(n < 1){
return 1;
}
return n * factorial(n - 1);
}
- 1
- 2
- 3
- 4
- 5
- 6
- 7
函数运行的示意图
factorial(6)
6 * factorial(5)
6 * (5 * factorial(4))
6 * (5 * (4 * factorial(3)))
6 * (5 * (4 * (3 * factorial(3))))
6 * (5 * (4 * (3 * (2 * factorial(1)))))
6 * (5 * (4 * (3 * (2 * 1))))
6 * (5 * (4 * (3 * 2)))
6 * (5 * (4 * 6))
6 * (5 * 24)
6 * 120
720
递归的思维要点
- 不要使用人肉递归
- 找到最近最简的方法,将其拆解成可重复解决的问题
- 数学归纳法
递归代码模板
代码模板不是绝对,如果不是非常标准的例题,多数情况都会有所不同,中间肯定有诸多细节不一样,但是大体流程很多是相似的,所以这里代码模板只是一种参考,记住有利于在对递归的理解。
Java 代码模板
public void recur(int level,int param){ //终结条件 if(level > MAX_LEVEL){ //process result // 处理结果 return; } //process current logic //处理当前的逻辑 process(level,param); //drill down //进入下一层 recur(level: level + 1,newParam); //restore current states //清理当前层的一些状态,主要是一些全局变量 }
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
回溯
什么是回溯
回溯算法实际上一个类似枚举的搜索尝试过程,主要是在搜索尝试过程中寻找问题的解,当发现已不满足求解条件时,就“回溯”返回,尝试别的路径。回溯法是一种选优搜索法,按选优条件向前搜索,以达到目标。但当探索到某一步时,发现原先选择并不优或达不到目标,就退回一步重新选择,这种走不通就退回再走的技术为回溯法,而满足回溯条件的某个状态的点称为“回溯点”。许多复杂的,规模较大的问题都可以使用回溯法,有“通用解题方法”的美称。
回溯法通常使用简单的递归来实现,在反复上述的步骤后可能出现两种情况:
- 找到一个可能存在的正确答案
- 在尝试了所有可能的分步方法后宣布该题没有答案
最坏的情况下,回溯会导致一次时间复杂度为指数时间的运算。
与动态规划的区别
- 共同点
- 用于求解多阶段决策问题。多阶段决策问题即:
- 求解一个问题分为很多步骤(阶段);
- 每一个步骤(阶段)可以有多种选择。
- 不同点
- 动态规划适合求最优解是多少,比如:最大/小值、是否满足/存在某种结果、组合数一共是多少。
- 回溯算法可以搜索得到所有的方案(当然包括最优解),但是本质上它是一种遍历算法,时间复杂度很高。
这里个人简单对比一下动态规划的经典算法“背包问题”和一般的优先搜索算法的对比,后面会有专门的文章总结背包问题。
- 背包问题是动态规划经典问题,适合求最优解,一般的01背包和完全背包简化递推公式后,时间复杂度都是O(VN),V是背包容量,N是物品数量。
- 搜索算法时间复杂度一般和N有关。
- 所以如果是面试的话,可以从下面几方面猜一下出题者的意思
- 题目是求最优解还是所有解,所有解就很可能是想考搜索算法。
- 如果是最优解:可以看一下算法题目给出V和N的范围,如果V很大一般是想要你使用搜索算法,如果N很大V不大,那么很可能是希望你使用动态规划。V和N的范围很可能会在题目末尾有提示,特别要注意。
回溯经典例题
全排序
给定一个 没有重复 数字的序列,返回其所有可能的全排列。
- 示例:
输入: [1,2,3]
输出:[[1,2,3],[1,3,2],[2,1,3],[2,3,1],[3,1,2],[3,2,1]]
来源:力扣(LeetCode) 链接:https://leetcode-cn.com/problems/permutations
著作权归领扣网络所有。商业转载请联系官方授权,非商业转载请注明出处。
这题是问所有的排列组合,那么很明显就是用搜索算法了。搜索过程其实就是一个多叉树。
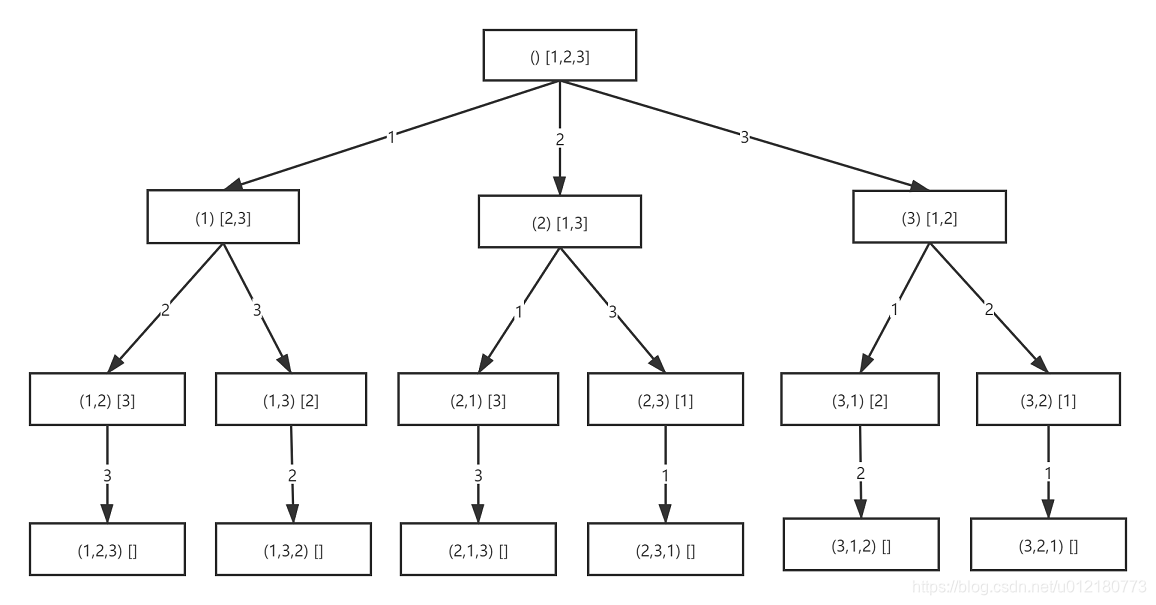
- 分解子问题:可以发现第一层分别可以取 1、2或者3,假如取1,剩下来的子问题就是1 + 子数组[2,3]的所有组合,然后再对子数组做同样的操作,直到叶子然后返回。
- 对于每一层的子问题,我们可以使用一个for循环,遍历数组的每一个数字,如果数字已经被使用则跳过,如果没有被使用则取出来。
class Solution { List<List<Integer>> res = new ArrayList<>(); List<Integer> list = new ArrayList<>(); boolean[] using; public List<List<Integer>> permute(int[] nums) { if(nums == null || nums.length == 0){ return res; } using = new boolean[nums.length]; helper(nums); return res; } private void helper(int[] nums){ if(list.size() == nums.length){ // 遍历到叶子,把结果存储起来,如何返回当前层 res.add(new ArrayList<>(list)); return; } for(int i = 0; i < nums.length; i++){ //标记位,表示当前搜索改元素已经被提取,不能在被使用。 //一次搜索就是从根结点到叶子 if(using[i]){ continue; } //添加到路径搜索 list.add(nums[i]); //标记元素被提取 using[i] = true; helper(nums); //递归返回后,表示当前层的子问题已经完成 //例如1和子数组[2,3]搜索完后,路径去掉1,开启下一个元素2的遍历 list.remove(list.size() - 1); //把当前元素从新标记为没使用 using[i] = false; } } }
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
时间复杂度:O(n!)
空间复杂度:O(n!)
全排列 II
给定一个可包含重复数字的序列 nums ,按任意顺序 返回所有不重复的全排列。
-
示例 1:
输入:nums = [1,1,2]
输出:
[[1,1,2],[1,2,1],[2,1,1]] -
示例 2:
输入:nums = [1,2,3]
输出:[[1,2,3],[1,3,2],[2,1,3],[2,3,1],[3,1,2],[3,2,1]] -
提示:
1 <= nums.length <= 8
10 <= nums[i] <= 10
来源:力扣(LeetCode) 链接:https://leetcode-cn.com/problems/permutations-ii
著作权归领扣网络所有。商业转载请联系官方授权,非商业转载请注明出处。
这题是在上面《全排列》的基础上,做了稍稍的改变:
- 数组包含重复数子
- 结果不能包含重复的排列
- 因此同一层的节点如果是相同的数字,不能重复遍历
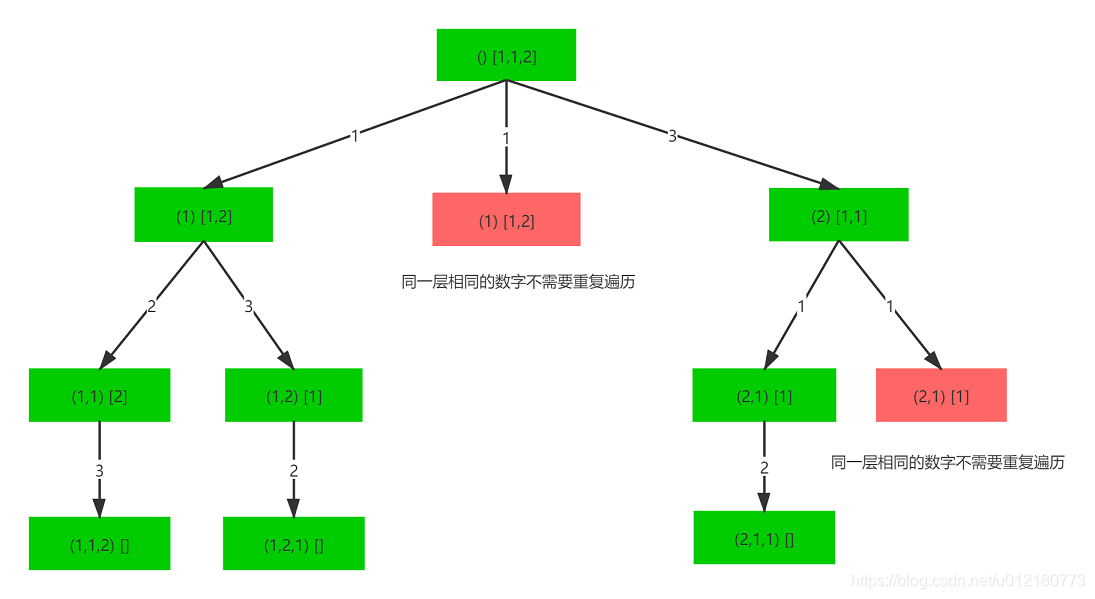
- 总体和上面《全排序》解题思路一样,添加了去重。
- 去重第一奥义:排序
- 对比当前节点是否和上一个节点相等,相等就跳过。
class Solution { List<List<Integer>> res = new ArrayList<>(); List<Integer> list = new ArrayList<>(); boolean[] using; public List<List<Integer>> permuteUnique(int[] nums) { if(nums == null || nums.length == 0){ return res; } using = new boolean[nums.length]; //去重先排序 Arrays.sort(nums); helper(nums); return res; } private void helper(int[] nums){ if(list.size() == nums.length){ // 遍历到叶子,把结果存储起来,如何返回当前层 res.add(new ArrayList<>(list)); return; } for(int i = 0; i < nums.length; i++){ //标记位,表示当前搜索改元素已经被提取,不能在被使用。 //一次搜索就是从根结点到叶子 if(using[i]){ continue; } //这里是去重的关键 //第一步判断是否和上一个相等,也就是重复数字,只遍历遇到的第一个 //判断using[i - 1] //如果是true表示表示两个相等的数字在同一条深度搜索路径上,而不是同一层节点,不能忽略。 //如果是false表示同一层的重复节点,忽略掉。 if(i > 0 && nums[i] == nums[i - 1] && !using[i - 1]){ continue; } //添加到路径搜索 list.add(nums[i]); //标记元素被提取 using[i] = true; //递归处理子数组 helper(nums); //递归返回后,表示当前层的子问题已经完成 //例如1和子数组[1,2]搜索完后,路径去掉1,开启下一个元素1的遍历 using[i] = false; list.remove(list.size() - 1); } } }
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
- 43
- 44
- 45
- 46
- 47
- 48
时间复杂度:最差O(n!)
空间复杂度:最差O(n!)
组合
给定两个整数 n 和 k,返回 1 … n 中所有可能的 k 个数的组合。
- 示例:
输入: n = 4, k = 2
输出:
[[2,4],[3,4],[2,3],[1,2],[1,3],[1,4]]
来源:力扣(LeetCode) 链接:https://leetcode-cn.com/problems/combinations
著作权归领扣网络所有。商业转载请联系官方授权,非商业转载请注明出处。
组合和上面《全排序》题目有两个不同
- 组合不考虑顺序,[1,2]和[2,1]是相同的组合,不能有重复,这个非常重要,是下面排序剪枝的前提!
- 集合有k个数的要求,这个需要考虑剪枝,比如当前路径节点数等于k了,就存储结果然后直接返回;或者如果当前子数组剩余个数小于k了,那么当前路径肯定没解,直接返回即可。这是经典的回溯问题。
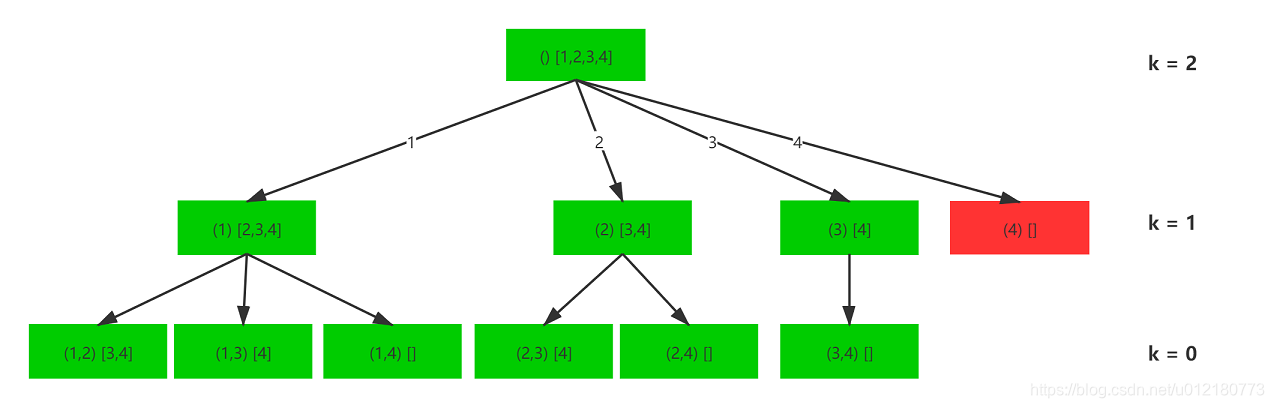
class Solution { List<List<Integer>> res = new ArrayList<>(); List<Integer> list = new ArrayList<>(); public List<List<Integer>> combine(int n, int k) { //k=0表示找到解,存储结果,然后返回 if(k == 0){ res.add(new ArrayList<>(list)); return res; } //剪枝: //如果当前层节点已经用完(k < 1);或者剩余节点数不足(k > n),表明当前路径没有解,直接返回 if(n < 1 || k > n){ return res; } //这里从n -> 1遍历,你也可反过来顺序遍历,因为题目结果集合元素没有顺序要求。 // for(int i = n; i > 0; i--){ //添加当前层路径节点 list.add(i); //和全排序不一样,同一层被遍历的节点,不能放到下一层的子数组里面,同时k需要-1。 //因为[1,2]和[1,2]是相同的解,先遍历的节点后后面的节点存在共同的真子集。 combine(i - 1,k - 1); //删除当前层路径节点 list.remove(list.size() - 1); } return res; } }
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
时间复杂度:O(n*…(n - k - 1))
空间复杂度:O(n…*(n - k - 1))
组合总和
给定一个无重复元素的数组candidates和一个目标数target,找出candidates中所有可以使数字和为target的组合。candidates中的数字可以无限制重复被选取。
-
说明:
所有数字(包括target)都是正整数。
解集不能包含重复的组合。 -
示例1:
输入:candidates = [2,3,6,7], target = 7,
所求解集为:[[7],[2,2,3]] -
示例2:
输入:candidates = [2,3,5], target = 8,
所求解集为:[[2,2,2,2],[2,3,3],[3,5]]
来源:力扣(LeetCode) 链接:https://leetcode-cn.com/problems/combination-sum
著作权归领扣网络所有。商业转载请联系官方授权,非商业转载请注明出处。
这里和上面《组合》题目有两个不一样的地方:
- 剪枝的条件有个数 k 变成了目标和 target
- 数字可以被重复使用(注意 for 循环中 i 的起始值,和传递到下一层的 level 的值)
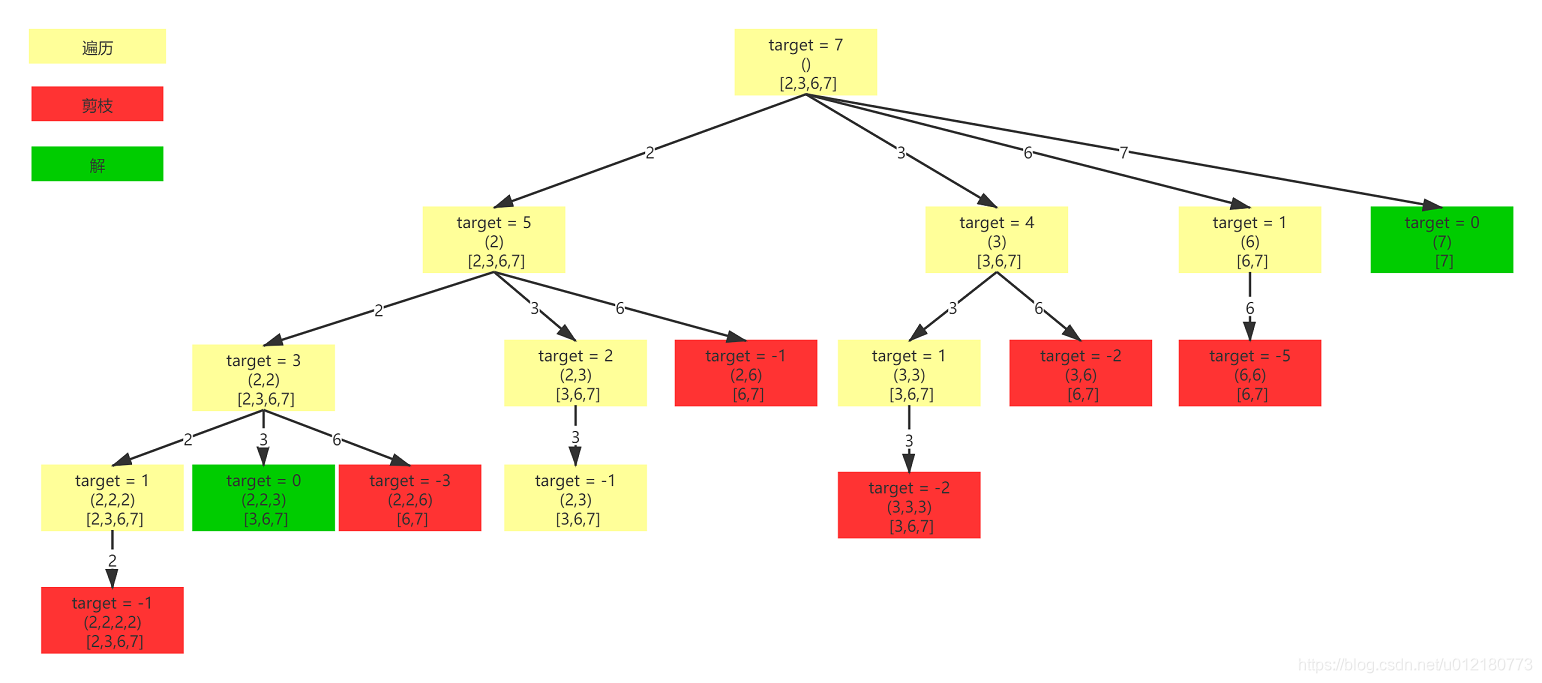
class Solution { List<List<Integer>> res = new ArrayList<>(); List<Integer> list = new ArrayList<>(); public List<List<Integer>> combinationSum(int[] candidates, int target) { //排序 //目标和剪枝的前提 //排序的时间复杂度O(logn),小于搜索本身,因此排序不会影响算法时间复杂度 Arrays.sort(candidates); //搜索辅佐方法 helper(candidates,0,target); return res; } private void helper(int[] candidates,int level,int target){ //target=0,表示搜索成功,存储结果 if(target == 0){ res.add(new ArrayList<>(list)); return; } //如果target小于子数组第一个元素,剪掉直接返回 //如果level == candidates.length表示已经是叶子节点,直接返回 if(target < candidates[level] || level == candidates.length){ return; } //遍历当前层的节点(上面图中的树的每一层) for(int i = level; i < candidates.length; i++){ //添加当前节点到搜索路径 list.add(candidates[i]); //递归子数组 helper(candidates,i,target - candidates[i]); //在搜索路径中删除当前层节点 list.remove(list.size() - 1); } } }
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
时间复杂度:O(S),其中S为所有可行解的长度之和。从分析给出的搜索树我们可以看出时间复杂度取决于搜索树所有叶子节点的深度之和,即所有可行解的长度之和。在这题中,我们很难给出一个比较紧的上界,我们知道O(n×2n)是一个比较松的上界,即在这份代码中,n个位置每次考虑选或者不选,如果符合条件,就加入答案的时间代价但是实际运行的时候,因为不可能所有的解都满足条件,递归的时候我们还会用 target - candidates[idx] >= 0 进行剪枝,所以实际运行情况是远远小于这个上界的。
空间复杂度:O(target)。除答案数组外,空间复杂度取决于递归的栈深度,在最差情况下需要递归O(target) 层。
组合总和 II
给定一个数组candidates和一个目标数target,找出candidates中所有可以使数字和为target的组合。candidates中的每个数字在每个组合中只能使用一次。
-
说明:
所有数字(包括目标数)都是正整数。
解集不能包含重复的组合。 -
示例1:
输入: candidates =[10,1,2,7,6,1,5], target =8,
所求解集为:[[1, 7],[1, 2, 5],[2, 6],[1, 1, 6]] -
示例2:
输入: candidates =[2,5,2,1,2], target =5,
所求解集为:[[1,2,2],[5]]
来源:力扣(LeetCode) 链接:https://leetcode-cn.com/problems/combination-sum-ii
著作权归领扣网络所有。商业转载请联系官方授权,非商业转载请注明出处。
和上面《组合总和》不同的地方:
- 这里数组的元素不可以重复使用。(注意 for 循环里面 i 的起始值和传递到下一层递归的 level 的值,和上面组合总和的比较看看有上面不一样!)
- 数组包含相同元素,但是解集不能存在重复的集合,因此同一层相等的节点不能重复遍历,这和《全排序II》相似的排序去重相似。
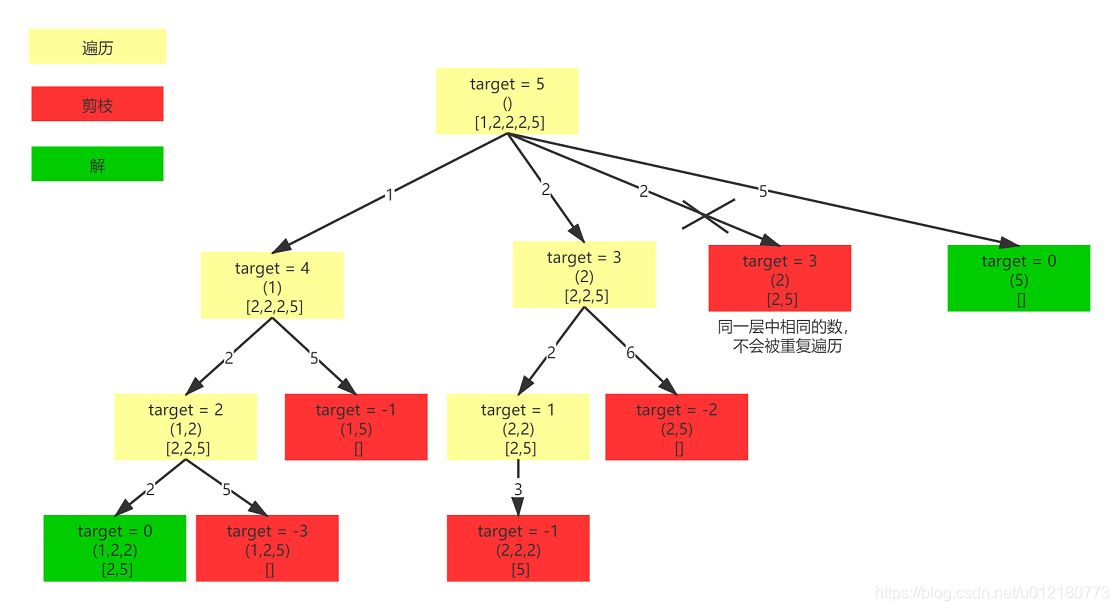
class Solution { //回溯 + 剪枝 //https://leetcode-cn.com/problems/combination-sum-ii/solution/hui-su-suan-fa-jian-zhi-python-dai-ma-java-dai-m-3/ List<List<Integer>> res = new ArrayList<>(); List<Integer> list = new ArrayList<>(); public List<List<Integer>> combinationSum2(int[] candidates, int target) { //排序去重和剪枝的前提,这和《全排序II》相似 Arrays.sort(candidates); //搜索辅佐方法 helper(candidates,0,target); return res; } private void helper(int[] candidates,int level,int target){ //找到解集的子组合 if(target == 0){ res.add(new ArrayList<>(list)); return; } //如果level == candidates.length表示已经是叶子节点,返回 //target < candidates[level]表示已经无法找到答案,直接剪掉,因为数组已经排序,而且都是整数。 if(level == candidates.length || target < candidates[level]){ return; } for(int i = level; i < candidates.length; i++){ //这里逻辑有点绕,我们把上面图中从顶点到叶子节点的路径称为“同一路径” //i == level 标识当前深度的第一个元素,由于相同元素都只能取第一个,后面的忽略 //如果i > level则表示是同一深度上的相同元素。 if(i > level && candidates[i] == candidates[i - 1]){ continue; } //添加当前节点值到当前搜索路径 list.add(candidates[i]); //递归下一层,这里 level 传递到下一层的值是 i + 1,因为元素在同一路径上不能被重复使用 helper(candidates,i + 1,target - candidates[i]); //从搜索路径移除当前节点值 list.remove(list.size() - 1); } } }
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
组合总和 III
找出所有相加之和为n的k个数的组合。组合中只允许含有1-9的正整数,并且每种组合中不存在重复的数字。
-
说明:
所有数字都是正整数。
解集不能包含重复的组合。 -
示例 1:
输入: k = 3, n = 7
输出: [[1,2,4]] -
示例 2:
输入: k = 3, n = 9
输出: [[1,2,6], [1,3,5], [2,3,4]]
来源:力扣(LeetCode)
链接:https://leetcode-cn.com/problems/combination-sum-iii
著作权归领扣网络所有。商业转载请联系官方授权,非商业转载请注明出处。
这题就是《组合》 + 《组合总和II》:
- 找出 k 个数的组合同时和为 n 。
- 每种组合不能使用重复的数字。(注意 for 循环里面 i 的起始值和传递到下一层递归的 level 的值,组合总和这几道题要相互比较!)
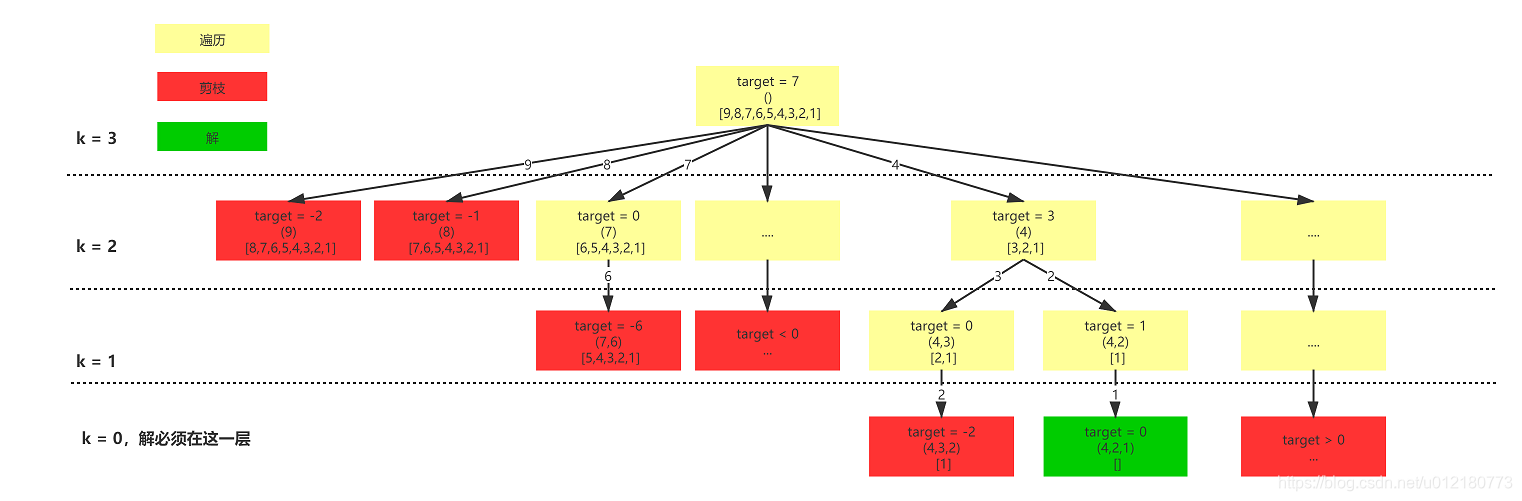
class Solution { List<List<Integer>> res = new ArrayList<>(); List<Integer> list = new ArrayList<>(); public List<List<Integer>> combinationSum3(int k, int n) { //这里是1...9的正整数,本来就是有序的,不需要排序 helper(k,n,9); return res; } private void helper(int k,int n,int v){ //k=0,n = 0:找到结果 if(n == 0 && k == 0){ res.add(new ArrayList<>(list)); } //k > v表示剩余的个数不足 //n > k * v表示剩下的子数组和肯定不足n //两种情况都剪掉 if(k > v || n > k * v){ return; } for(int i = v; i > 0; i--){ //添加当前节点到搜索路径 list.add(i); //递归子数组 helper(k - 1,n - i,i - 1); //从搜索路径中去除当前结点 list.remove(list.size() - 1); } } }
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
使用回溯搜索算法解决背包问题
下面这些题目都是非常典型的背包问题,本身的最优解法肯定是使用动态规划,但是正如标题“与动态规划的区别”介绍的那样,动态规划本身也是可以写成搜索算法的,所以这里尝试使用回溯搜索算法来进行接答,对比一下两种方法在解题上的差异。
组合总和IV
给定一个由正整数组成且不存在重复数字的数组,找出和为给定目标正整数的组合的个数。
- 示例:
nums = [1, 2, 3],target = 4
所有可能的组合为:
(1, 1, 1, 1)
(1, 1, 2)
(1, 2, 1)
(1, 3)
(2, 1, 1)
(2, 2)
(3, 1)
请注意,顺序不同的序列被视作不同的组合。因此输出为 7。
提示:
- 1 <= nums.length <= 200
- 1 <= nums[i] <= 1000
- nums 中的所有元素互不相同
- 1 <= target <= 1000
进阶:
- 如果给定的数组中含有负数会怎么样?
- 问题会产生什么变化?
- 我们需要在题目中添加什么限制来允许负数的出现?
来源:力扣(LeetCode) 链接:https://leetcode-cn.com/problems/combination-sum-iv
著作权归领扣网络所有。商业转载请联系官方授权,非商业转载请注明出处。
这是一道非常典型的完全背包问题,但是这里先从搜索算法的方式去分析它,初看上去和《组合总和》非常相似:
- 元素可以被无限次使用。
- 找出目标和的所有组合,不能有重复的组合。
但是不同的地方在于:组合元素的顺序不一样当作不同的组合
- 所以在《组合总和》中每个节点的下一层的分支数是不一样的,比如:数组 [1,2,3] 第二层第一个节点遍历了 1,那下一层依然有3个分支可以遍历 [1,2,3];但是第二层第二个节点遍历了2,那下一层只有2个分支,可以遍历 [2,3]。
- 但是这里不一样,因为顺序不同当作不同组合,所以当前层所有节点分支是一样的,也就是每一层的每个节点都有 3 个分支,所以如果 target 很大,而数组元素平均值又相对较小的话,树的节点数量是远大于 《组合总和》的。
我们先来看一下其搜索的分支树:
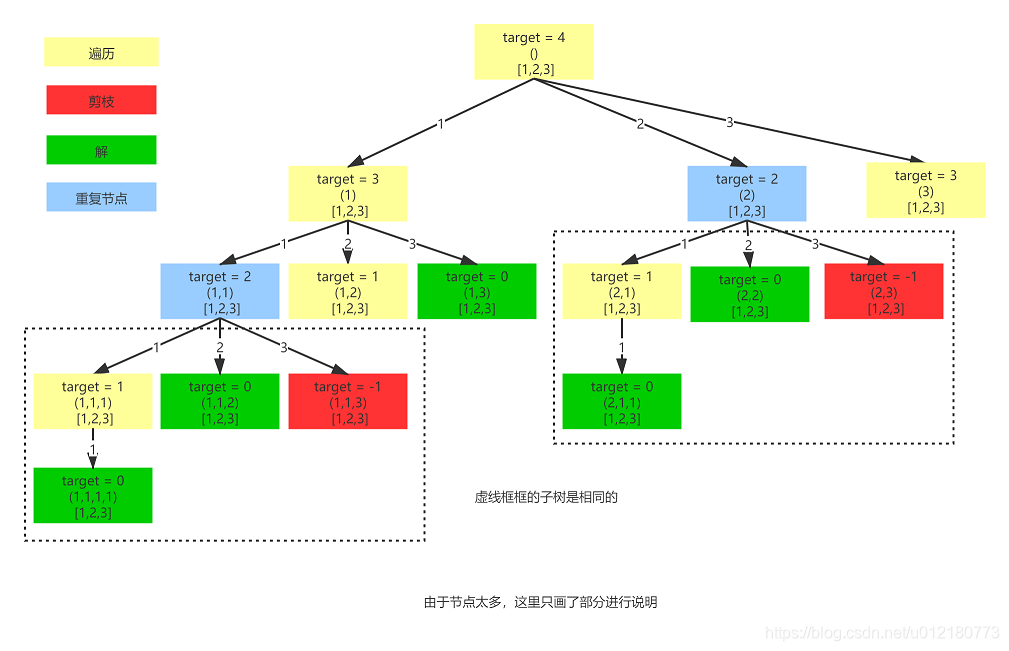
从上面图可以看出,递归树种存在大量的重复计算的节,比如蓝色标记的target=2的节点:一个解是(1,1)+ 子集;另外一个解是(2)+ 子集。而它们的子集是一样的,因为它们是一样的子问题,都是通过数组 [1,2,3] 求目标和为 2 的组合数,这会造成重复的计算,大大浪费计算资源,减低算法的效率。
不过呢,我们还是先尝试用最简单的方式去解答。
尝试1:直接递归搜索
class Solution { public int combinationSum4(int[] nums, int target) { int res = helper(nums,0,target); return res; } private int helper(int[] nums,int start,int target){ //找到结果 if(target == 0){ return 1; } //target < 0:表示后者的值都不可满足,因为没有负数,剪掉,直接返回0 //这里注意不能使用排序剪枝,因为这里顺序不同是不同的组合,它可以重复使用前面小的元素。 if(target < 0){ return 0; } int res = 0; for(int i = 0; i < nums.length; i++){ //当前层每个节点子数组的组合数相加,就是当前层总的组合数 res += helper(nums,i,target - nums[i]); } //返回当前层总的组合数 return res; } }
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
时间复杂度:O(n^m),n 是数组的长度,m 是树的平均深度,因为没办法无法通过排序剪枝,只能硬搜到target < 0,如果target非常大接近数组总和,那时间复杂度会非常高。
空间复杂度:O(1),除了递归栈之外不需要额外存储。
上面这个时间复杂度是没有办法通过leetcode测试的。正如我们前面所说的,树中存在大量重复计算的节点(这里要注意重复的含义:target 相等,同时往下搜索的子数组一样,如果有一样不一样,都不能当作同一个节点),因此我们可以给递归搜索添加记忆化,把所有计算过的结果存储起来,后面碰到相同节点直接获取结果就是。这里使用HashMap作为存储,put和get都是O(1)时间复杂度。
尝试2:回溯 + 记忆化
这里记忆化缓存 key 的结构本来应该是:
private static class Key{
private int target;
private int[] array;
}
- 1
- 2
- 3
- 4
但是由于元素可以被无限重复使用,所以往下搜索的子数组 array 都是一样的,所以这里可以直接使用 target 作为记忆化缓存的key。
class Solution { int[] memo = new int[1001];//提示中 target 的范围是 [1,1000]; public int combinationSum4(int[] nums, int target) { Arrays.fill(memo,-1); int res = helper(nums,target); return res; } private int helper(int[] nums,int target){ //target = 0 找到结果返回1 //target < 0:表示后者的值都不可满足,因为没有负数,剪掉,直接返回0 if(target <= 0){ return target == 0 ? 1 : 0; } //缓存存在结果,直接取出返回 if(memo[target] >= 0){ return memo[target]; } int res = 0; for(int i = 0; i < nums.length; i++){ //当前层每个节点子数组的组合数相加,就是当前层总的组合数 res += helper(nums,target - nums[i]); } //缓存当前target的结果 memo[target] = res; //返回结果 return res; } }
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
时间复杂度:因为每个真正需要计算的节点是0…target,每个节点有n个分支(n数组长度),而HashMap存取的时间复杂度是O(1),因此总的时间复杂度是O(target*n)。
空间复杂度:O(target),因为map需要存每个target的计算结果。
这样就能通过leetcode的测试了。
尝试3:动态规划
class Solution { public int combinationSum4(int[] nums, int target) { if(nums == null || nums.length == 0){ return 0; } int[] dp = new int[target + 1]; dp[0] = 1; //注意这里“背包容量” target 一定要在外层循环,因为元素顺序不一样是不同的解。 //因此每个容量 v 都需要利用前面 n 件物品和容量[0,v-1]计算结果,n 件物品需要多次循环,所以必须在里面。 //这个后面动态规划的文章再分析这两层循环如果交换顺序会有什么区别 for(int i = 1; i <= target; i++){ for(int n : nums){ if(n <= i){ dp[i] += dp[i - n]; } } } return dp[target]; } }
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
时间复杂度:O(target*n) ,时间复杂度和上面记忆化搜索一样,但是减少了递归栈的开销。
空间复杂度:O(target) 。
零钱兑换
给定不同面额的硬币coins和一个总金额amount。编写一个函数来计算可以凑成总金额所需的最少的硬币个数。如果没有任何一种硬币组合能组成总金额,返回-1。你可以认为每种硬币的数量是无限的。
-
示例1:
输入:coins = [1, 2, 5], amount = 11
输出:3
解释:11 = 5 + 5 + 1 -
示例 2:
输入:coins = [2], amount = 3
输出:-1 -
示例 3:
输入:coins = [1], amount = 0
输出:0 -
提示:
1 <= coins.length <= 12
1 <= coins[i] <= 231 - 1
0 <= amount <= 10^4
来源:力扣(LeetCode) 链接:https://leetcode-cn.com/problems/coin-change
著作权归领扣网络所有。商业转载请联系官方授权,非商业转载请注明出处。
如果从搜索算法的角度去分析,这题目和《组合总和》在场景几乎是一样的:
- 目标和==》总金额
- 数组==》不同面值的银币
- 数字可以重复使用==》硬币可以重复使用
不同的是:《组合总和》求的是所有解的集合,而硬币问题则是求最优解。所以就和文中开始对回溯和动态规划的对比说的那样,《组合总和》适合使用搜索算法,而硬币则适合使用动态规划, 因为零钱兑换其实也是经典的完全背包问题。
下面是零钱兑换的搜索分支树:
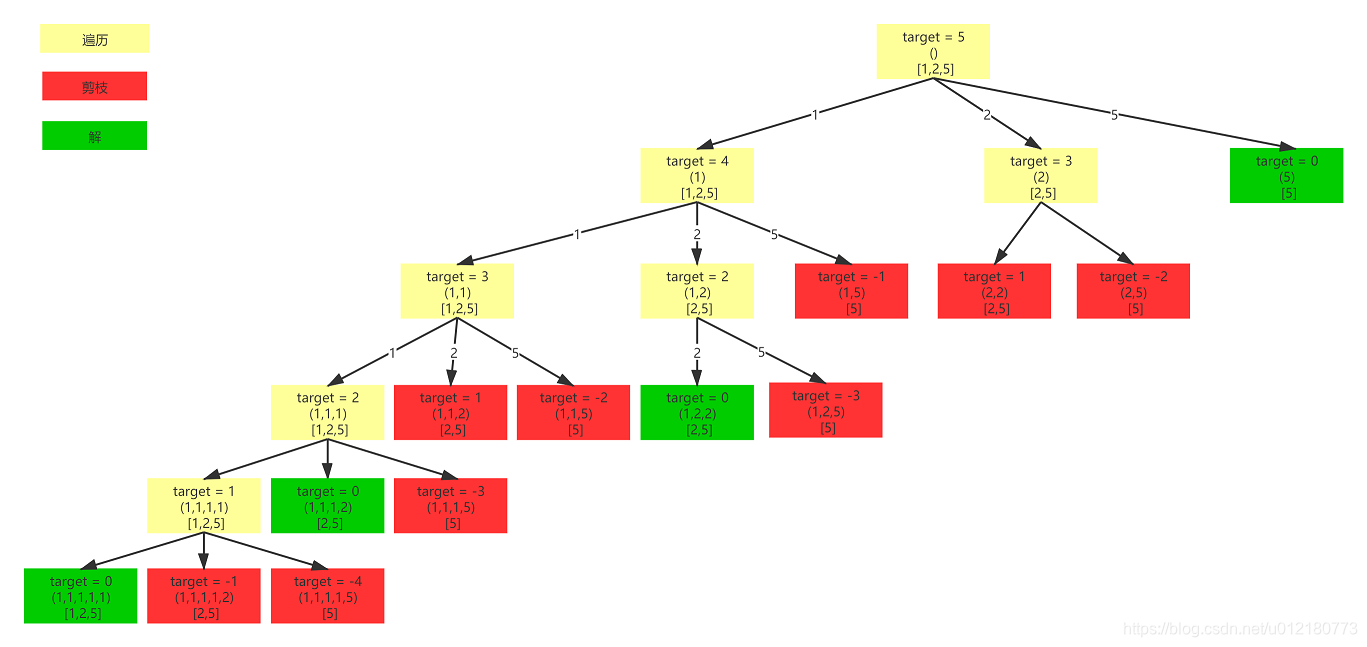
这里还是先尝试使用回溯+记忆化搜索的方式,目的是为了对比一下回溯搜索和动态规划的一些异同,加深这两方面的理解。
尝试1:回溯+记忆化搜索
这里记忆化缓存 key 的结构本来应该是:
private static class Key{
//target
private int amount;
private int[] array;
}
- 1
- 2
- 3
- 4
- 5
但是这个 key 的结构比较臃肿,我们可以化简一下:
- 从上面的分支树图可以看到 array 的下标范围是 [0…n,n],也就是右边界是不变的,变的是左边界,因此我们可以使用左边的起始下标作代替 array 作为 key 的其中一个标识。
- 题目中 coins.length <= 12,0 <= amount <= 10^4,也就是我们可以通过移位相加得到一个唯一值,把这个唯一值作为缓存的key
class Solution { //计算节点的唯一值作为缓存的 key //i 是当前 coins 子数组的起始下标,amount 是当前需要计算的组合和 private Integer getKey(int i,int amount){ return i * 100000 + amount; } Map<Integer, Integer> map = new HashMap<>(); public int coinChange(int[] coins, int amount) { //排序是剪枝的前提 Arrays.sort(coins); for(int i = 0; i < coins.length; i++){ map.put(getKey(i,0),0); } return helper(coins,0,amount); } private int helper(int[] coins,int start,int amount){ Integer key = getKey(start,amount); //如果缓存已经存在结果,则直接返回 if(map.containsKey(key)){ return map.get(key); } //如果后面路径不存在解了,则返回-1 if(start == coins.length || amount < coins[start]){ map.put(key,-1); return -1; } //当前层对比每一个结点的值,取最小的。 int count = amount + 1; for(int i = start; i < coins.length; i++){ if(amount < coins[i]){ continue; } int ret = helper(coins,i,amount - coins[i]); if(ret > -1){ count = Math.min(count,ret + 1); } } //保存当前节点的最小值 map.put(key,count == amount + 1 ? -1 : count); return map.get(key); } }
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
- 43
- 44
- 45
- 46

尝试2:动态规划
class Solution {
public int coinChange(int[] coins, int amount) {
int[] f = new int[amount + 1];
Arrays.fill(f,amount + 1);
f[0] = 0;
for(int i = 0; i < coins.length; i++){
for(int a = coins[i]; a <= amount; a++) {
f[a] = Math.min(f[a],f[a - coins[i]] + 1);
}
}
return f[amount] == amount + 1 ? -1 : f[amount];
}
}
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
从上面可以看到,动态规划的解法比第一种搜索算法要高出很多的,但是我们在一开始对比回溯和动态规划的区别的时候过:都是求最优解的情况下,如果 N(物品数量)很大,而 V(背包容量)较少则使用动态规划,因为动态规划的时间复杂度是O(VN),反之如果N不大,而V很大则使用搜索算法,搜索算法的时间复杂度一般只和N有关。
但是这里明明是 N(coins.length)很小,而 V (amount)很大,为什么搜索算法比动态规划慢那么多呢?一开始我也是不明白的,所以我去 leetcode 上去搜索了一些大佬的解法,终于发现了原来是我的搜索算法写的太烂了!
尝试3:回溯 + 排序剪枝 + 贪心
class Solution { private int ans = Integer.MAX_VALUE; public int coinChange(int[] coins, int amount) { //排序 Arrays.sort(coins); //必须从大到小开始遍历,这是减少时间复杂度的关键 //因为硬币面值越大,所需要的硬币数就也少,所以尽量找大的面值,这里是使用贪心算法 greedy(coins, amount, coins.length - 1, 0); return ans == Integer.MAX_VALUE ? -1 : ans; } // c_index 硬币下标 // count 硬币数量 void greedy(int[] coins, int amount, int c_index, int count) { //如果 amount == 0,对比最优解 if(amount == 0) { ans = Math.min(ans, count); return; } //如果起始下标 < 0 返回 if(c_index < 0) { return; } //贪心算法:优先找大面值的硬币,面值越大所需硬币数越少。贪心可能找到是局部最优解,但是局部最优解可以用于剪枝。 //贪心无法确定全局最优解,所以还是必须遍历所有可能路径,最后对比出最小值,但是大量的剪枝能让搜索效率大大提高。 for(int c = amount/coins[c_index]; c >= 0; c--) { //当前需要的总硬币数 int ncnt = count + c; //剩余的面值 int remain = amount - c * coins[c_index]; //如果为0,找到解,然后对比最优解 if(remain == 0) { ans = Math.min(ans, ncnt); } //如果当前所需硬币数大于或者等于当前最优解,则直接剪枝 //基于贪心,尽量小的解会在尽量早被找到,因此这里可以把大量的分支剪掉 if(ncnt + 1 >= ans) { break; } //否则递归下一层,继续凑剩余的面值 greedy(coins, remain, c_index - 1, ncnt); } } }
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
- 43
- 44

时间复杂度:最差是O(n^ m) + NlogN
- n 是数组长度,m 树的平局深度,后面的 NlogN 是数组排序的时间开销。
- 这道题的提示中给出,0 <= N <= 12,因此 NlogN 几乎可以忽略不记。m 是平均需要的硬币数量,但是基于贪心算法有大量的分支会被剪掉,尤其在 amount 比较大,硬币面值方差较大的时候,剪枝效果会特别明显,而这道题中的条件也恰恰是这样:1 <= coins[i] <= 231 - 1,0 <= amount <= 10^4。所以这里实际上的时间复杂度可能会远优于这个值。
空间复杂度:O(1) 。
对于这个解法,在 leetcode 有个大佬的评论我觉得很有参考价值就把它直接截图过来了:

零钱兑换II
给定不同面额的硬币和一个总金额。写出函数来计算可以凑成总金额的硬币组合数。假设每一种面额的硬币有无限个。
-
示例 1:
输入: amount = 5, coins = [1, 2, 5]
输出: 4
解释: 有四种方式可以凑成总金额:
5=5
5=2+2+1
5=2+1+1+1
5=1+1+1+1+1 -
示例 2:
输入: amount = 3, coins = [2]
输出: 0
解释: 只用面额2的硬币不能凑成总金额3。 -
示例 3:
输入: amount = 10, coins = [10]
输出: 1 -
注意,你可以假设:
- 0 <= amount (总金额) <= 5000
- 1 <= coin (硬币面额) <= 5000
- 硬币种类不超过 500 种
- 结果符合 32 位符号整数
来源:力扣(LeetCode) 链接:https://leetcode-cn.com/problems/coin-change-2
著作权归领扣网络所有。商业转载请联系官方授权,非商业转载请注明出处。
这题和上面《零钱兑换》条件一模一样,只是求解不一样,上面是求最优解,这里是求所有的组合数。
因此状态树也是和上面一致的,这里就不再画了,直接给出搜索算法和动态规划的解法。
尝试1:记忆化 + 回溯
Map<Integer,Map<Integer,Integer>> map = new HashMap<>(); public int change(int amount, int[] coins) { Arrays.sort(coins); for(int i = 0; i < coins.length + 1; i++){ Map<Integer,Integer> m = map.computeIfAbsent(i, k -> new HashMap<>()); m.put(0,1); } return helper(coins,0,amount); } private int helper(int[] coins,int start,int amount){ Map<Integer,Integer> m = map.computeIfAbsent(start, k -> new HashMap<>()); if(m.containsKey(amount)){ return m.get(amount); } if(start == coins.length || amount < coins[start]){ return 0; } int count = 0; for(int i = start; i < coins.length; i++){ count += helper(coins,i,amount - coins[i]); } m.put(amount,count); return count; }
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
尝试2:动态规划
class Solution {
public int change(int amount, int[] coins) {
int[] f = new int[amount + 1];
int n = coins.length;
f[0] = 1;
//这里一定要注意:物品数量一定要在外循环,否则会重复计数
//这个要和组合总和IV进行对比
for(int i = 0; i < n; i++){
for(int a = coins[i]; a <= amount; a++){
f[a] += f[a - coins[i]];
}
}
return f[amount];
}
}
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
最经典的回溯例题 - N皇后
n皇后问题研究的是如何将n个皇后放置在n×n的棋盘上,并且使皇后彼此之间不能相互攻击。

上图为 8 皇后问题的一种解法。
给定一个整数n返回所有不同的n皇后问题的解决方案。
每一种解法包含一个明确的n皇后问题的棋子放置方案,该方案中’Q’和’.'分别代表了皇后和空位。
-示例:
输入:4
输出:
[
// 解法 1
[".Q…",
“…Q”,
“Q…”,
“…Q.”],
// 解法 2
["…Q.",
“Q…”,
“…Q”,
“.Q…”]
]
解释: 4 皇后问题存在两个不同的解法。
提示:皇后彼此不能相互攻击,也就是说:任何两个皇后都不能处于同一条横行、纵行或斜线上。
来源:力扣(LeetCode) 链接:https://leetcode-cn.com/problems/n-queens
著作权归领扣网络所有。商业转载请联系官方授权,非商业转载请注明出处。
尝试1:回溯
class Solution { public List<List<String>> solveNQueens(int n) { //列 Set<Integer> cols = new HashSet<>(); //捺y = -x + b; Set<Integer> xysum = new HashSet<>(); //撇y = x + b; Set<Integer> xydiff = new HashSet<>(); List<List<String>> res = new ArrayList<>(); //递归回溯 helper(n,0,cols,xysum,xydiff,new ArrayList<>(),res); return res; } //逐行递归 //每行都遍历每一列,对齐往下一层递归 //每次递归都对当前行列进行检测,如果检测失败直接剪掉,然后返回 //如果递归到叶子节点,也就是路径长度为行数量,表示找到一个解 //行列(x,y)检测:皇后可以攻击行、列和两个对角线 //所以每行/每列/每个对角线都只能有一个皇后。 //行:是遍历的层数,每次只添加一个节点,所以肯定唯一 //列:每次添加一个格子到搜索路径,就把列数缓存到相应的Set,之和如果列数在set中不存在,表示检测通过,否则冲突 //捺:y = -x + b -> y + x = b,如果b一样则表示在同一条对角线上。 //撇:y = x + b -> y - x = b,如果b一样则在同一对角线上。 private void helper(int n,int row,Set<Integer> cols,Set<Integer> xysum,Set<Integer> xydiff, List<String> list,List<List<String>> res){ //找到结果 if(n == row){ res.add(new ArrayList<>(list)); return; } char[] chars = new char[n]; Arrays.fill(chars,'.'); for(int col = 0; col < n; col++){ //检测当前格子是否能放置皇后 //如果列/撇/捺中有一个已经放置了棋子,则不能再放置,跳过。 if(cols.contains(col) || xysum.contains(row + col) || xydiff.contains(row - col)){ continue; } //把当前格子标记为设置皇后 chars[col] = 'Q'; //如果通过,缓存当前列/撇/捺的数据到Set中 cols.add(col); xysum.add(row + col); xydiff.add(row - col); //添加当前格子到搜素路径 list.add(String.valueOf(chars)); //递归处理下一行 helper(n,row + 1,cols,xysum,xydiff,list,res); //恢复当前行状态 //重新把当前格子标记为空 chars[col] = '.'; //从列/撇/捺中移除当前格子的数据 cols.remove(col); xysum.remove(row + col); xydiff.remove(row - col); //从搜索路径中移除当前格子 list.remove(list.size() - 1); //继续遍历当前行的下一列 } } }
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
- 43
- 44
- 45
- 46
- 47
- 48
- 49
- 50
- 51
- 52
- 53
- 54
- 55
- 56
- 57
- 58
- 59
- 60
- 61
- 62
- 63
时间复杂度:O(n!)。单纯从递归来看的话,最差时间复杂度是O(n^ n),但是考虑到每次找到一个皇后,剩下只有找n - 1个皇后,其他的被剪枝掉了,时间复杂度是O((n - 1)^(n - 1)),因此总的时间复杂度是O(n * (n - 1) * …*1),即是O(n!)。
空间复杂度:O(3 * n),每一个皇后一次缓存(列/撇/捺),最多同时存在n个皇后。
其实N皇后更加优的解答是回溯 + 位运算,但是这里主要是讲回溯算法,位运算的解法后面位运算的总结文章再给出相应的代码。



