互动抽奖背后的随机性与算法实现

背景

抽奖，是一种典型的互动玩法形式。无论是大V的粉丝抽奖，还是活动会场的参与抽奖，这种起源于彩票开奖的互动玩法，同时兼顾了高期待感和低预期的特征，让活动在成本控制之余又能有惊喜和引爆点，这样的优势让其在各种运营场景中幻化万千，大行其道。
在闲鱼各种互动场与营销活动中，抽奖自然也是一个相当高频使用的互动玩法。众所周知，越是经典的玩法，业务需求就越发别出机杼，在参与条件、开奖展示、奖品规则等各方面千变万化，闲鱼内典型的就有现金夺宝、低碳双十一抽iphone、旧衣回收抽锦鲤等，不胜枚举。

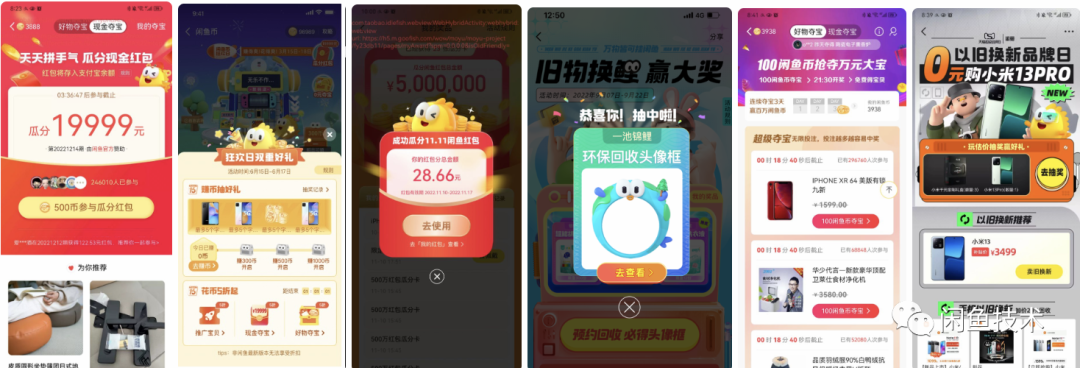
本系列文章的出发点即是从技术的视角出发，讲一讲抽奖这种互动玩法自底向上的各种思考。而本文主要探讨的，就是抽奖随机性的来源和常用的算法实现。

关于随机

抽奖最需要保证的，其实是公平的产生抽奖结果，而这个公平，则来自于足够随机的抽奖算法，而抽奖算法不论怎么设计，常常依赖于计算机随机数的发生。不妨先来看一看万仞之基础——随机数是怎么产生的。

伪随机数与其产生——线性同余

为了效率和成本计，现在常用的随机数的产生方式往往是伪随机数，最广为流行的就是线性同余产生器，其本质非常直白：

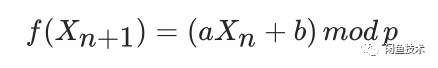
不难看出，其中的a、b、p的取值，就是是否能产出随机分布的数据根本所在。基本数论的常识告诉我们，这个同余式的取值必定在[0,p-1]的范围内封闭，并且拥有最大为p的周期，或者是多个较小但互不重合的周期构成，当其周期为p时，其式就成为了0到p-1的一个离散排列。
之所以这个看似简单的式子，能够成为随机数的生成方法，正是因为模数运算的良好特性，一来其在周期内绝不会出现重复结果，二来其分布也相对均匀。可以将f(x)/p视为[0,1)范围内的平均分布。

参数取值

所以，我们的第一个问题，就必然是探索，在参数满足什么条件时，能将这个函数的周期尽可能的扩大，以更有效的利用其周期特性，挖掘这个式子产出的随机性。
我们先从模数p开始，不论其他，光凭数学直觉就会让人下意识的想取一个大素数，以此轻易攫取优越的分布特性和天然形成的宽周期。
但是，我们要注意到，伪随机数作为一个非常底层的方法，其存在本身就是为了效率的，取模操作虽然不算慢，但此时就会有一个更加优越的模数跃入眼帘，那就是2^n——不但可以直接将取模操作退化为移位和与操作，也可以很轻松的理解随机数的取值范围。当然，这个周期比起素周期也更方便均分以转化为其他范围的随机函数。

当然，模数不是素数的情况下，就对a、b的取值有了更大的约束。为了取得一个满周期序列的生成方法，The Art of Computer Programming中论证了其充要条件，也是现在大部分线性同余产生器的构造依据：

• • b与p互质

• • c=a-1是p所有素因子的倍数

• • 若p是4的倍数，c也是4的倍数

我们可以看到，这其中对加数b的约束其实非常小，于是在gcc中，就比较随意的选择了个12345，java中干脆是个小素数11。而对于a的取值，在已知我们取模数为2^n时，就非常容易得知其约束条件：a-1是4的倍数。

实现时的考量

现在我们满怀欢喜的得到一个满周期序列的生成方法，似乎只需要按照某些特性去选一些优秀的生成参数就可以跑起来成为一个经典库了。但事情还没有这么简单。
刚才我们的选择还遗留了一个问题，我们往往不是直接使用一个全模数范围的随机，而是由大周期的随机数取模转化为一个更小的周期来随机——只要大范围的随机函数能保证概率均等，取模后自然也是一个均匀分布的函数：

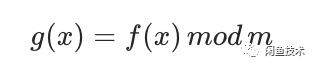
——但是以上方式有一个天然的缺陷，当我们的模数m与2的幂次相关时，其低位随机性并不是很好——低位周期的分布也会在这个小周期上呈现周期，形式化地说，就是：

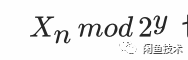
也总是一个满周期序列，所以，无论怎么去改变参数分布，在模数非素的情况下，随机的分布都会呈现一个特别均匀的形式，当我们想取得范围特别小时，比如我们只需要0-1的整数，这个算法就会持续输出0、1、0、1、0、1、0、1。当然，它仍然是满周期的，但是呈现出的结果完全违背了我们对于“随机”这件事的直觉，可预测性太强了。

这个时候，我们重新回顾一下，就会发现，我们想要的其实不是满周期的随机性，当周期非常小的时候，我们更期待的是超越本周期的随机性分布，比如，给0-1的随机安排一个00101110这样的周期序列，这个要求在本周期的计算比较难达成的，但是既然这个小周期是由一个更大的周期序列摘取到的，我们就能够将大周期的随机性反映到小周期当中去。
很多平台的实现当中，是舍弃这些随机性不强的低比特位，换为截取高位比特位作为结果序列，这样当然会导致该序列一些很好的数列特性消失，但是从而也增强了其本身的随机性。

比如在java的实现中：

private final AtomicLong seed;
 
private static final long multiplier = 0x5DEECE66DL;
private static final long addend = 0xBL;
private static final long mask = (1L << 48) - 1;
 
protected int next(int bits) {
    long oldseed, nextseed;
    AtomicLong seed = this.seed;
    //这里有一把自旋锁，保证每次输出不相同
    do {
        oldseed = seed.get();
        nextseed = (oldseed * multiplier + addend) & mask;
    } while (!seed.compareAndSet(oldseed, nextseed));
    //这里截取的是高位比特值
    return (int)(nextseed >>> (48 - bits));
}

使用中的细节

其实到这里，随机数的生成问题我们基本上已经摸清楚了，既然我们知道了随机数的发生过程，其实就很容易抓住重点，那就是随机数种子才是最为重要的，随机数只是一种生成过程，甚至说理解为一种可持续的hash方式也无不可。随机数的随机性完全来自于你随机数种子的随机性。所以在习惯中，我们常常会使用当前毫秒时间作为种子，而在java里的默认种子生成如下：

public Random() {
    this(seedUniquifier() ^ System.nanoTime());
}
 
private static long seedUniquifier() {
    // L'Ecuyer, "Tables of Linear Congruential Generators of
    // Different Sizes and Good Lattice Structure", 1999
    for (;;) {
        long current = seedUniquifier.get();
        long next = current * 181783497276652981L;
        if (seedUniquifier.compareAndSet(current, next))
            return next;
    }
}
 
private static final AtomicLong seedUniquifier
    = new AtomicLong(8682522807148012L);

可以看到，为了避免不传种子的情况出现，java默认提供了一个种子，这里也有把自旋锁，加上随机数生成本身的那一把，可以看到随机数发生在多线程的情况是会导致竞争的（虽然损耗很低），所以在阿里巴巴开发规约中会推荐使用ThreadLocalRandom中的随机数来生成。
如果你还记得上面的内容，还可以看出，这个种子本身也是个线性同余发生器发出的随机数，只不过特殊一点，是b=0情况下的乘法发生器。这种发生器的周期必定无法满周期，但是对于生成“随机种子的因子”这种情况，够用。
有点黑色幽默的是，虽然这里堂而皇之的标明了这里的常数来源于Tables of Linear Congruential Generators of Different Sizes and Good Lattice Structure 这篇论文，但是实际上181783497276652981这个数并不存在于论文推荐的表现最佳的因子中，看上去这里是一个Typo——数字开头少打了个1，但是实际上大家也知道了，一个“不那么完美”的分布其实也没那么有所谓。

随机数的生成原理并不复杂，整体的实现也是非常简洁直白的，但这其中又包含了很多精巧的构思，最终达到了一种效率与结果的统一，技术的美感往往就分布在这些简单而不失优雅的实现当中。当然，任何算法都有自己的适用范围，伪随机数在密码学意义上并不足够安全，如果是对于随机性有着强需求的场景，我们应当使用其他的随机数生成方法。

关于公平的抽奖算法

"公平"的维度

提到抽奖，大家最先想到的，一定是，如何保证抽奖的公平性？
而在开始这一部分前，笔者想先阐明一个观点，公平是多维度的，存在用户视角上的公平，客观意义上的公平，算法上的公平等等多种意义上的公平。
比如我们完全可以将一种名之为“抽奖”的东西概率设为100%，然后用库存限制抽中，这样所谓抽奖就退化为秒杀，在没有任何暗箱操作的情况下，我们可以说这是完全公平的，但是客观上来说，也可以认为，对网较差、设备性能不佳或晚了一点参与的用户是相当不公平的。
所以，反直觉的一点是，其实抽奖的算法也可以不那么公平，因为在任何一个拥有大量参与用户的活动中，用户的参与已经带来了大量的随机性上的因子，在没有提前看过参与用户的前提下，就算由一个值班同学一拍脑袋说今天是第4090位用户中奖，在某种程度上也是个相当公平的算法。所以，抽奖算法也是最容易设计的算法——因为无论你产出的结果分布有多糟糕，也很难被“开盒”唾骂。
实际上，在实践经验中，我们往往更要保证的是，结果的存在性和及时性，也就是说，无论你通过什么手段开出来奖，一定要在约定时间内发到有效的用户手上——延迟与无效是工程上能体现出的最致命的问题。

真正应该看重的维度

不过，除了公平性之外，抽奖其实还有很多其他维度的业务考量：
1、抽奖机会限制，是只能单次参与？还是能一次性多注参与？还是能反复追加的多次参与？
2、开奖时机限制，是希望即时开奖？还是接受参与结束后定时开奖？
3、奖品分布限制，是所有用户争夺唯一大奖？还是分一二三奖的奖品序列？还是瓜分红包或者积分的面额？人人有奖还是基本无奖？
4、并发系统性能限制，同时来参与、来领奖的用户规模和qps如何？是否会影响演算时间和接口延时？
根据业务目标的不同，实际开发中，主要还是根据这些维度的特征实现特定的抽奖算法，以下列举几种常用的抽奖算法：

当抽奖的奖品粒度是个时

1）选中法

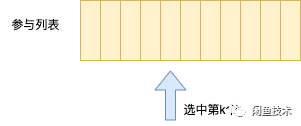
在得知所有参与用户的情况下，我们可以每次直接生成1-n的随机数的方式，抽出中奖用户的编号。
这种方法的缺陷是有可能会造成碰撞，需要考虑如何剔除已经中过奖的用户。但是对于用户规模很大的活动来说，碰撞的概率极低，这种方法是最快速的。
当然，我们上面也说过，这个方法无论使用的是怎样天花乱坠的随机函数，并不比你拍脑袋写几个固定数字更高明，还不会遇到碰撞。
闲鱼内的“百币夺宝”就采用的此方案，因为每个夺宝活动都是唯一的奖品，与用户约定了选中的号码规则，就可以方便快捷的找出中奖用户。

2）洗牌法

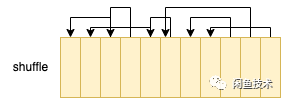
洗牌法是对整个中奖名单进行一次shuffle，彻底乱序后留在特定位置的用户成为中奖用户。一般认为这种方法造成的I/O次数是最多的，但还是有很多手段可以进行优化的，比如分区处理。它也存在着最佳的应用场景，比如当一个活动人人都能中基本不同的奖品时。
除此之外，它与选中法一样，实施的前提条件，也是必须获得全部的参与用户信息然后处理，对于实时想获知中奖信息或者想快速开奖的活动并不适用。

3）蓄水池抽样法

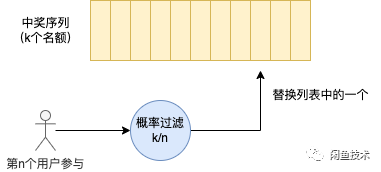
抽奖本身也可以视作一种抽样，那么蓄水池抽样法就是一个非常适用的开奖法，它在参与人数未确定时就可以开始运作。我们维护一个大小为奖品数量k的奖池，每个用户过来都有k/n的机会与奖池内一个中奖者进行交换，其中n为当前参与规模。可以证明，这样所有用户的中奖记录仍然是均等的。
抽样法本质上可以视作shuffle的一种优化，利用参与人数与中奖规模的差异，免去了一些无用的swap操作。但这个优化会带来两点不同，一来，活动时刻维护着中奖列表，可以让活动终止在任何时刻并即刻开奖，无需等待至所有用户参与完毕后再演算开奖；二来，其容错性和鲁棒性会大大提升，很容易并行化，在参与数量比较巨大的情况下，前后执行产生的概率变化非常微小，而且中间任何一个用户操作出错，都不会对系统整体带来什么关键影响。
闲鱼内的“回收抽锦鲤”就采用的此方案，对于各不相同的奖品列表，维护大小为k的中奖者列表，最终留在列表内的就是中奖者。

瓜分类型的算法，比如瓜分现金红包或者积分，抽奖的粒度是分

4）瓜分红包算法

最著名的自然是微信的瓜分红包算法，每个人瓜分的红包额度是这样计算的，先给每个人瓜分0.01元，然后加上rand(0~剩余平均红包金额的两倍)，而最后一个人拿到剩余所有钱。
这个算法可以保证大家瓜分的期望金额是相同的，但方差会越来越大，从而导致中最大奖的概率在各位置上是不同的。局限性在于，这个算法还是利用了一个先验信息，即参与人数n，需要发红包者预先选择好能领取的数量。
其最大的优势是不需要等到所有参与信息都获得之后进行，可以实时开奖。但同时，最大的问题是因为强依赖了“红包剩余金额”这个信息，并发性会比较差，往往还是需要提前演算出结果，无法应对实时高并发的场景。
闲鱼内的现金夺宝就采用了这种算法，但是由于参与规模特别巨大，往往是将奖池与参与用户划分为若干批次再进行的开奖。

“不公平”但最好用的抽奖算法

5）概率法

有时候我们希望用户能即时开出奖来，这个时候我们并不知道整场活动的全貌，只能靠一些先验的经验来决定当前用户的中奖概率，在发奖时实时由概率计算用户是否中奖，比如在奖池内提前规定A奖品中奖概率30%。
但概率法并不公平。由于奖品数量有限，库存会消耗光的缘故，对于固定中奖概率来说，后来的中奖概率是小于原来的中奖概率的，假设我们仅有一个奖品一个库存的话，每个人过来的中奖概率应当需要为

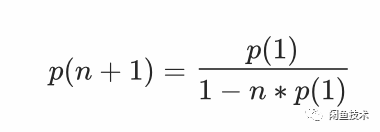
，才能保证用户无论什么时候参与概率都是相等的。可以看到，这个式子不但计算麻烦，会产生并发问题，居然还有规模限制。而有多个库存的情况下，情况将会更复杂。
实际场景中上我们还有很多其他因素的干扰，特别是业务本身的决策，比如我们并不希望一开始就放出所有库存，中途才放出一点点库存。或者我们希望中奖库存是随着时间过去均匀的消耗掉的，这样我们就有更多的动机去调节这个本来就不公平的概率算法。所以说，概率法，是离客观公平最远的算法。
但是，我们一开始的讨论也说明，这部分的不公平只是存在于理论上，如果我们没有人为操控使特定人中奖，在任何用户都是黑盒的情况下，我们还是可以认为，这是公平的，因为用户没有机会判断得知，究竟这个活动的概率分布呈现什么样的情况，从而实现套利。用户只能通过一些经验化的谣言，比如“大额券总是在活动末期要冲量时才会放出”，或者“活动初期中奖概率更高”，来控制参与时机进行博弈。
所以，这里的“不公平”打上了引号，事实是概率法由于其充分的运营空间和简明的规则，反而成为应用最广的抽奖方式。
值得一提的是，概率法可以采用“概率保持”策略来应对部分奖品库存耗尽或者命中限中的情况，即该部分概率由其他奖品按概率比例再分配，也可以简单做到保证必中。

在工程实现上，以上的算法其实都可以在规模到一定程度时，进行分布式优化，将奖池和参与者分而治之；也完全可以在方法间互相结合，来达到想要的业务效果。

小结

本篇文章从随机数和抽奖算法两个基础的层面，浅显地探讨了一些关于互动抽奖的内容，从最底层实现层面形叙述了抽奖的基本逻辑，但万丈高楼平地起，选定了算法，只是实现十万百万级在线用户参与的抽奖互动玩法的第一步。实际上，抽奖作为在无数互动场都屡试不爽的玩法，在业务实践中有着更复杂的场景与问题，接下来还有关于权益发放，关于用户驱动，以及关于抽奖玩法模型本身的更多内容，敬请期待。