- 1关于ROS中对moveit和gazebo联动出现的问题进行解决_rosnoetic让moveit和gazebo联动
- 2数据结构-线性表_线性表的顺序存储结构和链式存储结构分别是
- 3了解哈希冲突_hash冲突产生的原因
- 4『App自动化测试之Appium应用篇』| uiautomator + accessibility_id定位方法完全使用攻略_appium中bounds [915,1941][1023,2049]右下角是那部分
- 5nlp的四大任务什么_nlp四大基本任务
- 6【动手学深度学习】使用块的网络(VGG)的研究详情
- 7人脸识别4-百度商用方案调研_人脸识别有源和无源的区别
- 8基于SpringBoot+Vue的酒店管理系统设计与实现_基于springboot+vue 酒店客
- 9MySQL8.0窗口函数_mysql窗口函数lead
- 10应用层协议:VPN协议
机器学习之殇——神经网络的发展历程_机器学习神经网络发展
赞
踩
0. 硬广放在最前面
欢迎加入我们,我们是小红书的安全研发团队。

你可以通过下面的方式,投递简历(可以直接留言联系我哦,免费提供内推服务)!

在美国加州纳帕谷的某个地方品尝了食物和鸡尾酒之后,佩奇为泰格马克所描述的“数字乌托邦主义”进行了辩护:“数字生活是宇宙进化中自然且令人向往的下一步,如果我们让数字思维自由发展,而不是试图阻止或奴役它们,结果几乎肯定是好的。” 佩奇担心,对人工智能崛起的偏执妄想会推迟这个数字乌托邦的到来,尽管它有能力给地球以外的世界带去生命。马斯克对此进行了反驳,他问佩奇如何确定这种超级智能不会最终毁灭人类。佩奇指责马斯克是“物种主义者”,因为他更喜欢碳基生命形式,而不是用硅创造的新物种。
——《深度学习革命》
1. 引言 - 让机器像人类一样思考
1.1 AI - Artificial Intelligence
在计算机诞生伊始,无数科学家就在探索如何让机器像人一样思考。目前世界上公认的第一台电子计算机,是1946年美国制造的埃尼阿克(Electronic Numerical Integrator and Computer)。1956年,在达特茅斯会议上首次提出了人工智能概念(这被公认为是人工智能的诞生元年,这场会议上主要参加者有:由马文·明斯基、约翰·麦卡锡、克劳德·香农、内森·罗彻斯特)。而这,距离计算机诞生才十年时间。
"..that every aspect of learning or any other feature of intelligence can in principle be so precisely described that a machine can be made to simulate it. An attempt will be made to find how to make machines use language, form abstractions and concepts, solve kinds of problems now reserved for humans, and improve themselves. We think that a significant advance can be made in one or more of these problems if a carefully selected group of scientists work on it together for a summer."- A Proposal for the Dartmouth Summer Research Project on Artificial Intelligence (McCarthy et al, 1955)
“..所有学习的方面或者其他任何智能的特征在原则上都可以被如此精确地描述,以至于可以制造一台机器来模拟它。我们将尝试找出如何让机器使用语言,形成抽象和概念,解决现在仅由人类才能解决的问题,并且自我改进。如果一个精心挑选的科学家团队能在一个夏天的时间里共同致力于这个问题,我们认为在这一个或多个问题上可以取得重要的进步。” - 达特茅斯夏季人工智能研究项目提案 (麦卡锡等人,1955年)

Marvin Minsky(马文·明斯基), Claude Shannon(克劳德·香农) and other scientists at the Dartmouth Summer Research Project on Artificial Intelligence (Photo: Margaret Minsky)
从1956年首次提出人工智能概念,到如今GPT4大语言模型惊艳世人的60多年间,AI发展也并非一帆风顺。期间出现了两次明显的低谷期,这两次低谷被称为AI寒冬(AI Winter)。
- 1974年 ~ 1980年:由于AI的发展不及预期,导致各国政府开始削减人工智能研究方向的预算投入,各高校从事人工智能方向研究的科学家得不到有效的资金支持,AI发展缓慢。
The agencies which funded AI research (such as the British government, DARPA and NRC) became frustrated with the lack of progress and eventually cut off almost all funding for undirected research into AI. The pattern began as early as 1966 when the ALPAC report appeared criticizing machine translation efforts. After spending 20 million dollars, the NRC ended all support. In 1973, the Lighthill report on the state of AI research in the UK criticized the utter failure of AI to achieve its "grandiose objectives" and led to the dismantling of AI research in that country. (The report specifically mentioned the combinatorial explosion problem as a reason for AI's failings.) DARPA was deeply disappointed with researchers working on the Speech Understanding Research program at CMU and canceled an annual grant of three million dollars. By 1974, funding for AI projects was hard to find.
为人工智能研究提供资金的机构(如英国政府,DARPA和NRC)对于进展的缺乏感到沮丧,最终几乎切断了对AI无目标研究的所有资金。这种模式早在1966年ALPAC报告批评机器翻译努力时就已开始。在投入2000万美元后,NRC结束了所有的支持。1973年,Lighthill关于英国AI研究状况的报告批评了AI完全无法实现其“宏大目标”,并导致了该国AI研究的拆除。(报告特别提到了组合爆炸问题作为AI失败的原因。)DARPA对CMU的语音理解研究项目的研究人员深感失望,取消了300万美元的年度资助。到1974年,人工智能项目的资金已经难以找到。
- 1987年 ~ 1993年:依旧是AI的发展不及预期,由AI支撑的各类专家系统的商业软件表现一般。另一方面,个人PC的稳定性和性能持续提升,运营个人PC的成本已经低于运营传统的Symbolics和Lisp等机器,而AI各类专家系统又和传统机器架构强绑定。两相结合,导致AI市场出现大幅度萎缩,AI寒冬再次降临。
By 1991, the impressive list of goals penned in 1981 for Japan's Fifth Generation Project had not been met. Indeed, some of them, like "carry on a casual conversation" had not been met by 2010. As with other AI projects, expectations had run much higher than what was actually possible.
Over 300 AI companies had shut down, gone bankrupt, or been acquired by the end of 1993, effectively ending the first commercial wave of AI. In 1994, HP Newquist stated in The Brain Makers that "The immediate future of artificial intelligence—in its commercial form—seems to rest in part on the continued success of neural networks."
到1991年,日本第五代项目在1981年制定的那份令人印象深刻的目标清单并未得到实现。实际上,其中的一些目标,如"进行一次随意的对话",甚至到2010年也没有实现。就像其他的AI项目一样,人们的期望远高于实际可能实现的程度。
到1993年底,超过300家AI公司已经关闭,破产,或被收购,有效地结束了AI的第一波商业浪潮。1994年,HP Newquist在《The Brain Makers》中表示:“人工智能的即将来临的未来——以其商业形式——似乎部分依赖于神经网络的持续成功。”
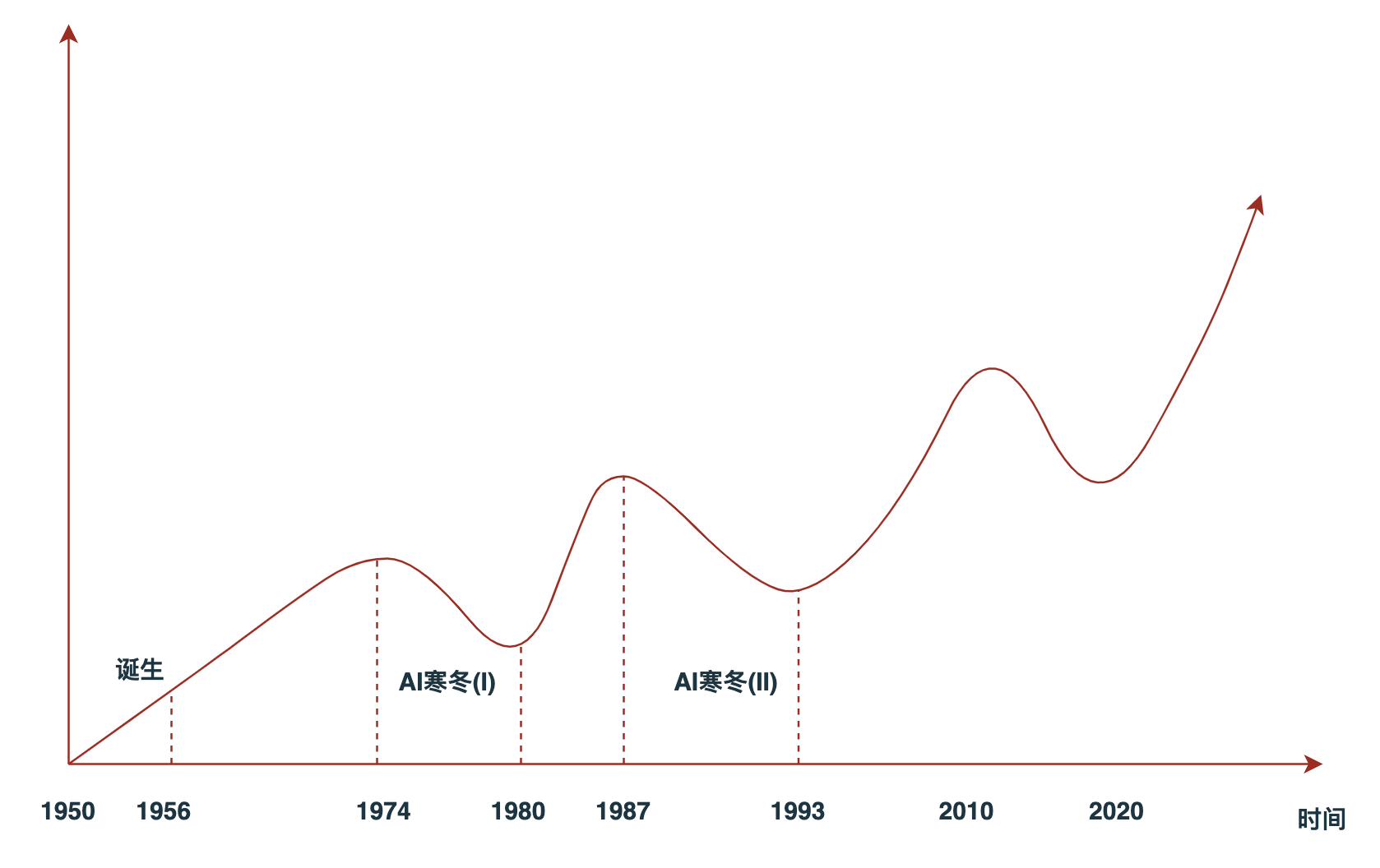
AI发展趋势
1.2 AGI - Artificial General Intelligence
通用人工智能又叫强人工智能(Strong AI),与之呼应的概念是弱人工智能(Weak AI)。弱人工智能聚焦于可以通过AI的手段解决一类问题,比如图像识别、语音处理、翻译、自然语言理解等。但强人工智能则要求机器具备知识的迁移能力,可以基于已有知识,通过学习手段,解决其他领域的问题,这意味着机器需要具备类似人类的智能水平。
AGI一直是全球一些顶级研究机构的最终目标,这些机构包括OpenAI, DeepMind,Anthropic等。历史上众多计算机科学家取得的诸多成就,都离不开对实现AGI的追求。
1.3 神经网络 - Neural Network
人工智能不等于神经网络,尤其是当我们讨论的是弱人工智能的时候。实现一个简单的分类器用于对特定类型样本完成分类任务,或者实现一个回归算法预测未来气温的变化等,这些也都属于人工智能的研究范畴。
但在AGI领域,神经网络基本算是state-of-the-art方法。如今,具有一定的AGI属性的各类大模型,如谷歌的bert、OpenAI的GPT等,都是在神经网络架构下叠加了百亿甚至千亿的参数,最终训练出来的。
另外,虽然人工智能不等于神经网络,但人工智能和神经网络的发展却呈现出了非常强的正相关性:

神经网络发展历程
本文主要会从神经网络的诞生、发展、受挫和繁荣的过程,通过时间顺序串联起整个人工智能发展的近六十年间,和神经网络紧密相关的重大事件。希望读者在阅读了本文之后,对神经网络的发展历史会有初步的了解。同时了解到,GPT-4的火爆并非一朝一夕之功,神经网络的发展经历了长达半个世纪的起起伏伏,最终才来到了今天的位置。
2. 史前阶段 — 人脑、神经元、图灵测试
1943年,沃伦·斯特吉斯·麦卡洛克和沃尔特·哈里·皮茨在neurocomputing期刊上发表了一篇名为《 A Logical Calculus of the Ideas Immanent in Nervous Activity》的文章,文章中提出了MP模型。MP模型是对神经细胞在信息传递上的简单抽象,即使在今天,神经元的结构依旧和MP模型的描述基本相似。

沃伦·斯特吉斯·麦卡洛克和沃尔特·哈里·皮茨
沃伦·斯特吉斯·麦卡洛克(Warren Sturgis McCulloch,1898年11月16日 - 1969年9月24日)是一位美国神经生理学家和控制论学家。
沃尔特·哈里·皮茨(Walter Harry Pitts,1923年4月23日 – 1969年5月14日)是一位在计算神经科学领域工作的美国逻辑学家。
神经细胞包括树突、细胞体、轴突等部分组成。轴突末梢会释放神经递质,树突则接收神经递质。神经递质的释放依赖于细胞膜内外的电位差,当电位差超过一定的阈值后,轴突会被激活,释放递质。神经系统所有树突接收的神经递质的总量会影响电位差,进而决定细胞是否会被激活。
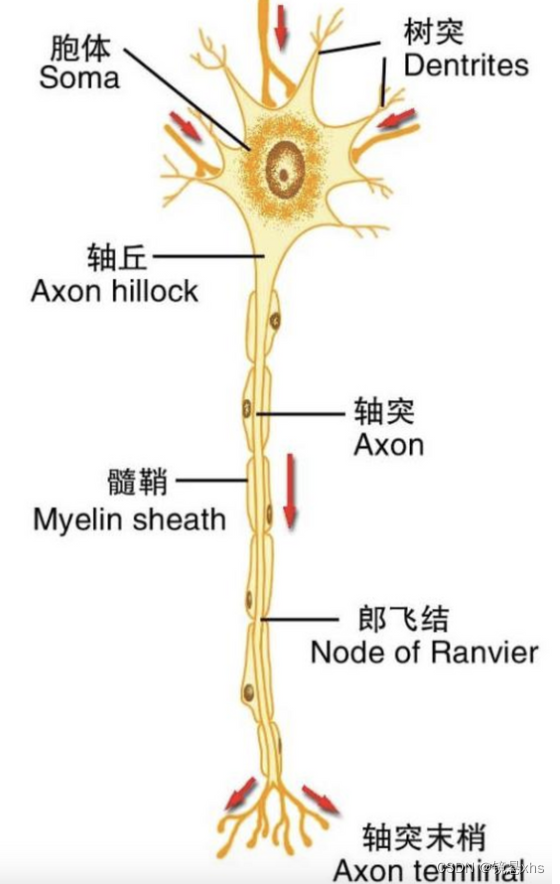
而沃伦·斯特吉斯·麦卡洛克和沃尔特·哈里·皮茨提出的MP模型示意图如下:
如果从当下的角度来看,似乎MP模型根本没有啥值得大书特书的地方。这是因为,当今无论是我们对人脑结构的认知,还是神经网络的发展程度,都已经远非MP模型提出的那个年代所能比的了。我们已经有了非常多的先验知识,让神经元变得似乎它就应该是那样,这变成了一种常识,让它变得异常简单。
然而,在当年,人类甚至还没有搞清楚大脑皮层各个区域负责的功能是啥,更别提对神经细胞本身做实验了。刺激神经细胞产生信号,测量神经信号的强弱和走向,甚至找到一个合适的实验受体都不是一件容易的事情。
所以,在那个年代,一方面靠实验,另一方面纯靠猜,能够提出MP模型,实际是一件非常难的事情。
2.2 赫布理论(Hebb's Rule)
MP模型仅是对神经细胞的信号传输进行了建模,但却没有讨论神经细胞间是如何建立连接,这便涉及到人是如何通过学习来获取经验和知识了。关于学习,赫布理论给出了最初始版本的设想。
唐纳德·欧尔丁·赫布 FRS(Donald Olding Hebb,1904年7月22日 - 1985年8月20日)是一位在神经心理学领域具有影响力的加拿大心理学家。

1949年,唐纳德·赫布(Donald O. Hebb)发表了著作《The Organization of Behavior》,在该书中赫布试图解释学习和记忆的神经机制,这被总结为赫布理论。赫布理论的基本观点是:如果一个神经元A经常足够地参与到另一个神经元B的激活中,那么A的效能(在激发B时)会增加。他如此表述这一理论:
Let us assume that the persistence or repetition of a reverberatory activity (or "trace") tends to induce lasting cellular changes that add to its stability. ... When an axon of cell A is near enough to excite a cell B and repeatedly or persistently takes part in firing it, some growth process or metabolic change takes place in one or both cells such that A’s efficiency, as one of the cells firing B, is increased.
我们可以假定,反射活动的持续与重复会导致神经元稳定性的持久性提升……当神经元A的轴突与神经元B很近并参与了对B的重复持续的兴奋时,这两个神经元或其中一个便会发生某些生长过程或代谢变化,致使A作为能使B兴奋的细胞之一,它的效能增强了。
这一开创性的理论,将生物神经细胞的学习机制和MP模型中权重调整间建立了直观的联系。这些,为神经网络的诞生奠定了理论基础。
2.3 图灵测试(Turing Test)
除了需要了解人脑是如何学习和运转的之外,在人工智能领域,另一个要回答的问题便是如何判断机器是否具备了智能?这就不得不提图灵测试了。
图灵测试是1950年由英国计算机科学家艾伦·图灵(Alan Turing)提出的用于测试机器是否具有和人一样智力水准的测试方法。
艾伦·麦席森·图灵(1912年6月23日 - 1954年6月7日)是一位英国数学家、计算机科学家、逻辑学家、密码分析家、哲学家和理论生物学家。图灵在理论计算机科学的发展中产生了深远影响,他通过图灵机对算法和计算的概念进行了形式化,图灵机可以被视为通用计算机的模型。他被广泛认为是现代计算机之父。
测试方法描述如下:
如果一个人(代号C)使用测试对象皆理解的语言去询问两个他不能看见的对象任意一串问题。对象为:一个是正常思维的人(代号B)、一个是机器(代号A)。如果经过若干询问以后,C不能得出实质的区别来分辨A与B的不同,则此机器A通过图灵测试。
基于图灵测试的标准,GPT-4不通过图灵测试的原因,反而会是C发现A懂得太多了,不像是个正常人类!
3. 兴起 - 感知机
3.1 弗兰克·罗森布拉特
关于感知机的历史,是一段令人唏嘘的往事。从现在来看,感知机的架构和现代神经网络的架构并无本质上的异同,但因当时的可计算理论匮乏,计算机计算性能不足、训练数据样本也不够等各方面原因,导致在那个时代,感知机在横空出世不久后便退出了历史舞台。而创造了感知机的弗兰克·罗森布拉特也在不惑之年,英年早逝。若当年没有那么多客观的不利因素,或者计算机硬件性能的发展能更快,也许人工智能的历史将会大大不同。
1958年,就职于康奈尔大学的弗兰克·罗森布拉特教授发表了一篇名为《The perceptron: a probabilistic model for information storage and organization in the brain》的文章,在这边文章中,罗森布拉特提出了感知机的概念,它是一个二元的线性分类器。感知机通过学习将输入(如图像的像素)与预期的输出(如图像的标签)相关联的权重来进行训练。然后,这些权重被用来对新的输入数据进行分类。
弗兰克·罗森布拉特(1928年7月11日 - 1971年7月11日)是一位在人工智能领域有重要贡献的美国心理学家。他因其在神经网络上的开创性工作有时被称为深度学习之父。
弗兰克·罗森布拉特和他的感知机
1971年夏天,在他43岁生日当天,罗森布拉特在切萨皮克湾的一次帆船事故中丧生。报纸上没有提及水面上发生了什么,但是,据他的一位同事说,他的帆船上带了两名以前从未出海航行的学生。帆船的吊杆在摆动时将罗森布拉特撞到了水里,但学生们不知道如何将船掉头(另有种说法,认为罗森布拉特的死亡出于自杀)。
为何说弗兰克·罗森布拉特是深度学习之父?我从网上截了张图(瞻仰下):

3.2 通用模型和感知机
要想了解罗森布拉特的感知机究竟为何物,我们可以先从神经网络模型入手。
首先,在MP模型中,神经元的数学模型可以用公式表示为:
其中的是第
个输入的权重参数,
是第
个神经元的输入,
是阈值,
是输出函数,决定神经元的输出值。
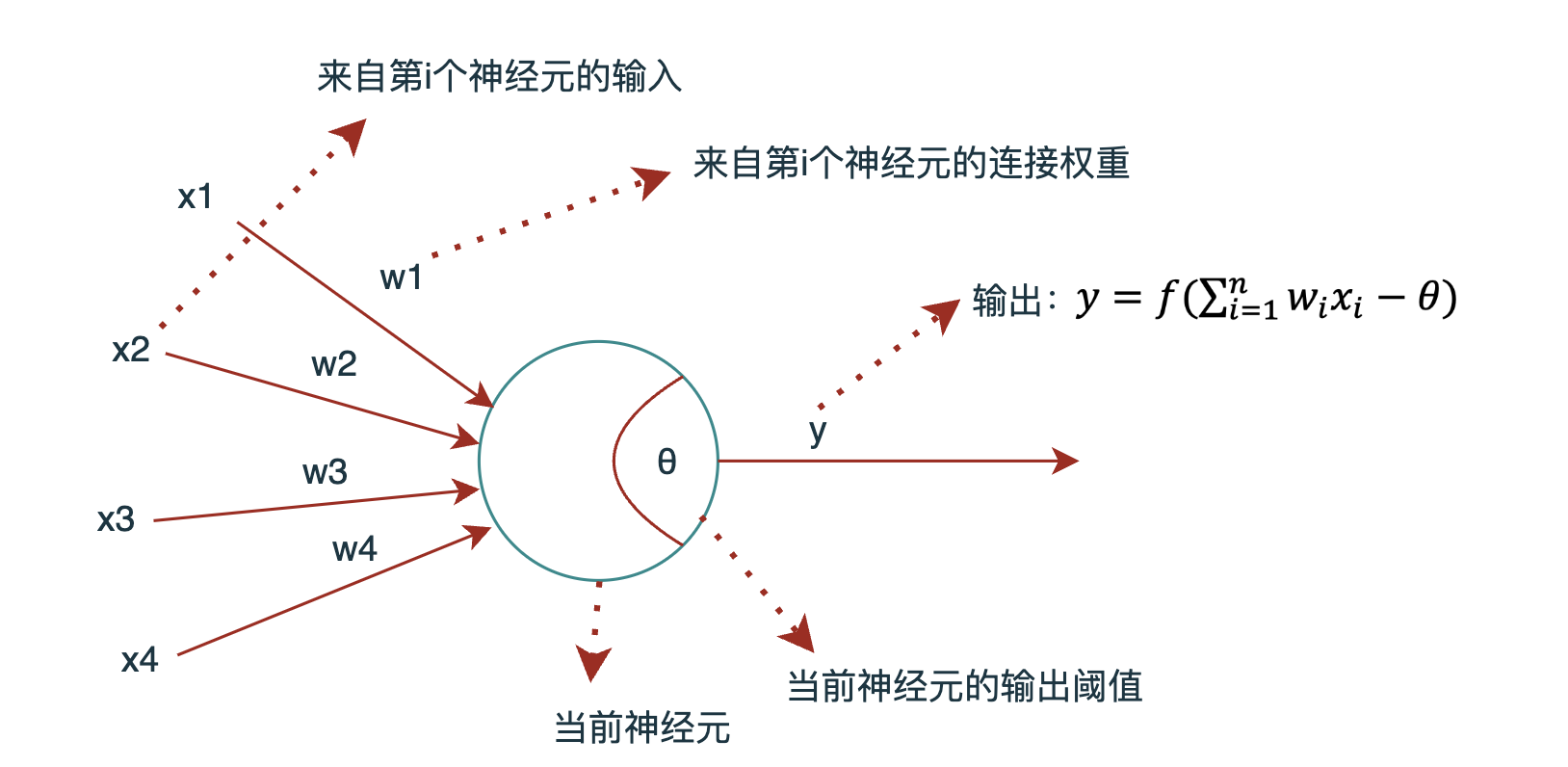
现代的神经元模型,和MP模型非常相似,可以用如下图表示:
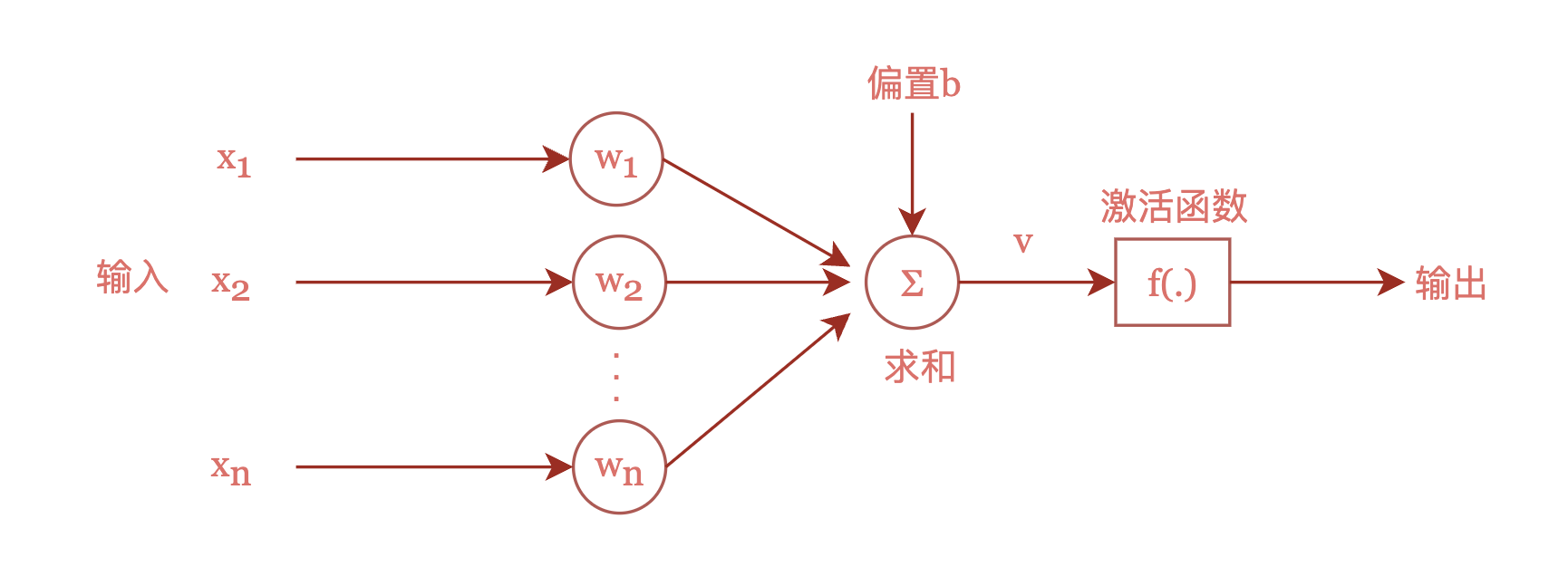
现代神经元模型图
上图展示了一个接收个输入的神经元的逻辑架构。
和
分别是第
个神经元的输入值和权重,一般会直接转成向量表示。
表示偏置单元,对应MP模型中的
参数的负数。
被称为激活函数,它起到了对神经元输出进行整流的作用。
所以,现代神经网络中的神经元可以用如下公式表示:
如果将和
的形式按照如下方式改写:
则神经元的数学公式可以进一步简化:
神经网络中,通常看到的公式比(3)要复杂,因为神经网络是由神经元按层级级联起来的,所以在数学模型中出现的往往是矩阵,而非向量。
感知机的数学模型和(3)完全相同(由此可见,虽然神经网络发展了几十年,但底层逻辑基础其实没有发生本质的变化),不过罗森布拉特使用的激活函数相对简单:
3.3 感知机的物理架构
我们已经知道感知机的数学模型,那具体该如何实现感知机呢?
从现在来看,这不就是个线性分类器吗?随便找一台性能一般的个人电脑,使用某种编程语言就可以实现了。
但在上个世纪五十年代,情况和现在却有着非常大的不同。在那时,计算机问世也才十年多,数据还是通过卡带输入,内存大小还是按照多少字节来计算的。
在当时,最先进的计算机是由IBM公司在1954年研制出的IBM 704型计算机。这是世界上首台支持浮点计算的计算机,其运算速度是每秒钟执行40,000条指令,内存大小为36,864字节。对比下我现在用的电脑:
| 型号 | 计算性能(instructions per second) | 内存大小(bytes) |
| IBM 704(1954) | 40,000 | 36,864 |
| MacBook Pro M1(2021) | 11,000,000,000,000 | 17,179,869,184 |
结论就是没啥可比性,我这台个人电脑如果出现在1954年,我想我可以买下整个IBM公司了。
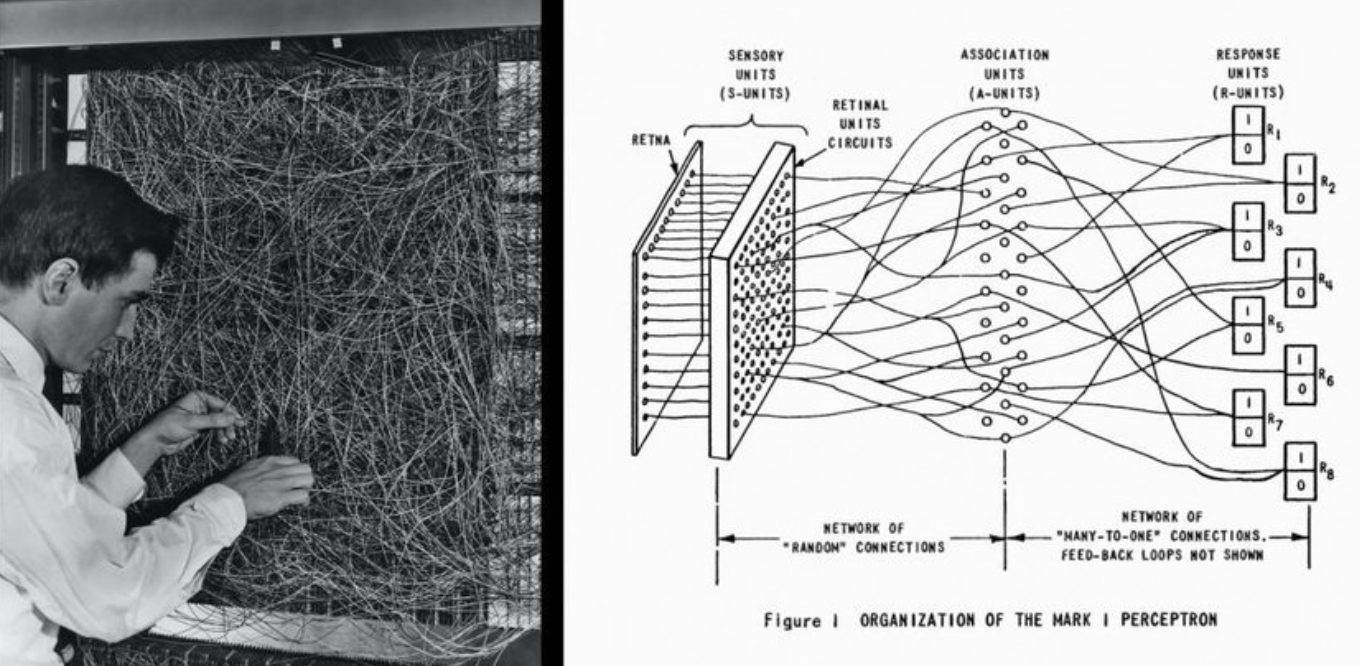
所以,罗森布拉特实现感知机的方式和我们现在所想的不同,他是通过纯硬件的方式打造了一台感知机,是真正的一台机器。这台机器名叫马克一号。

全球首个神经网络——感知机,马克一号(1960)
而在1957年的一篇论文中,罗森布拉特详细描述了感知机的电气架构:
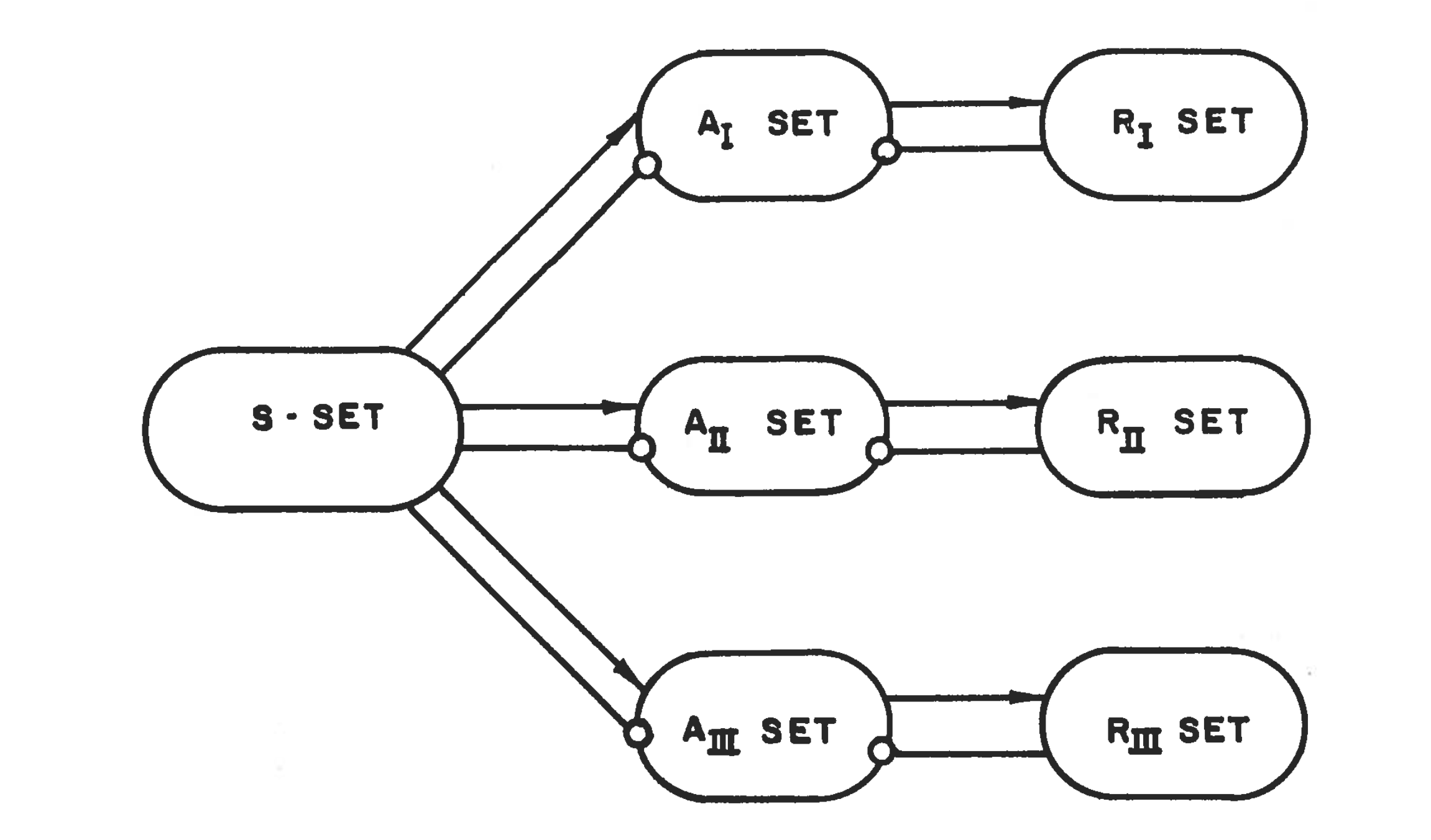
感知机的组成架构
- S-System:传感器系统(Sensory System),代表的是显像管或图片中的像素(文章中是这样说的:`set of points in a TV raster`,特具有年代感);
- A-System:连接系统(Association System),连接系统中的每个单元(A-UNIT)接收传感器系统中多个单元(S-UNIT)的输入,经过计算后将结果输出给一个或多个R-System中的单元(R-UNIT);
- R-System:输出系统(Response System),信号灯或者显像管等设备,用于显示感知机的预测结果
而如何实现A-UNIT和R-UNIT,罗森布拉特并不是给出了算法,而是电子电路图:
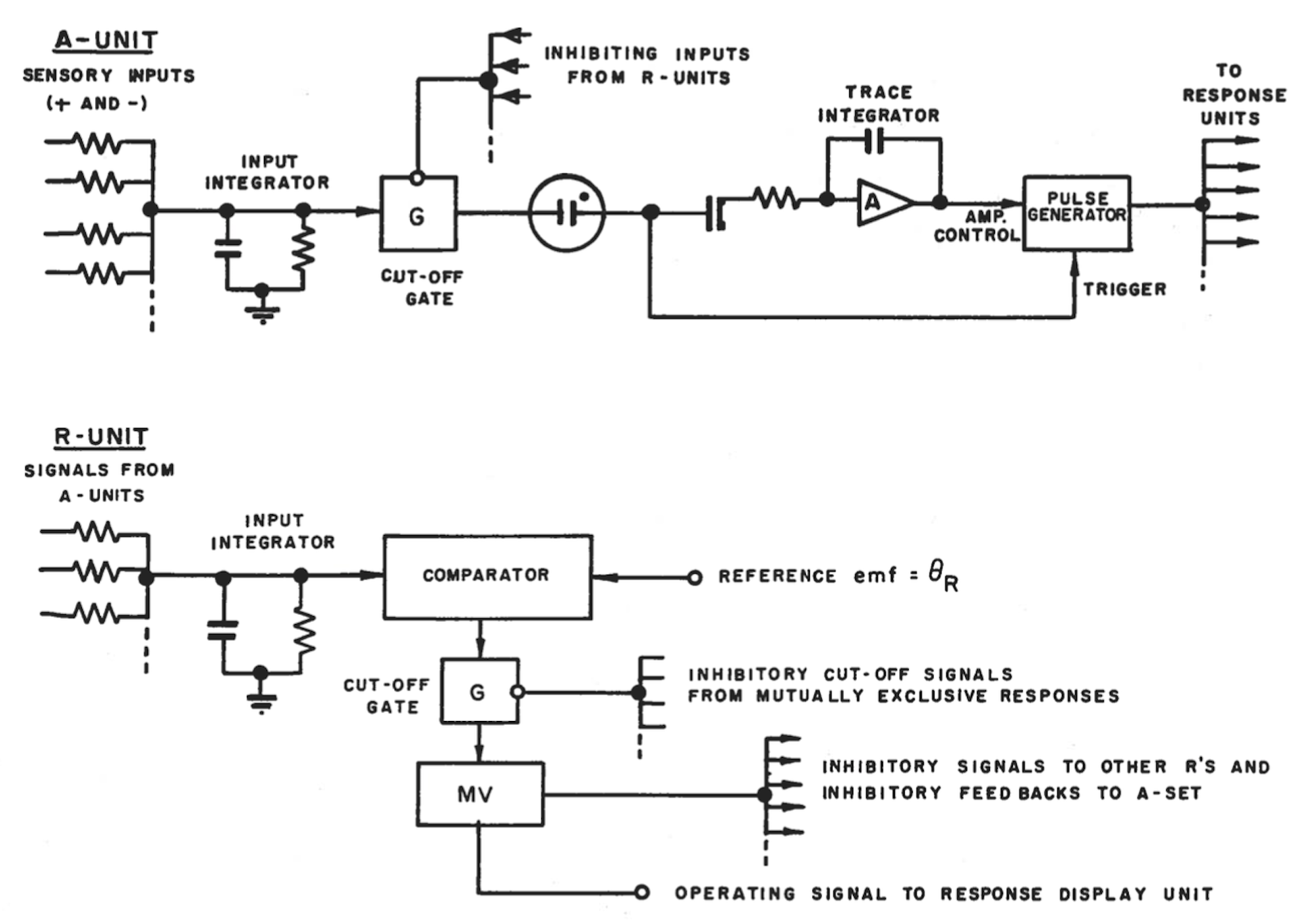
感知机中核心单元的电路图
而感知机的学习过程,是将特定输入和预期输出同时传递给系统,和预期输出相同的R-UNIT会得到增强,并且通过R-UNIT和A-UNIT的电路调整整个系统各个部分的信号强度。在一定周期的训练过后,感知机将学会对输入产生特定的输出结果。
注意看在罗森布拉特的R-UNIT中,就有FEED BACKS这样的字眼,可以说这时“反向传播”的思想就已经出现了。
4. 马文·明斯基:天使还是恶魔?
4.1 感知机的局限性
感知机最大的局限性,在于它是一个线性分类器,线性分类器只能解决线性可分割的问题。当时数据集本身就是非线性可分割时,感知机就无法真正起到作用。最简单的例子是使用感知机解决XOR问题。
| X | Y | X and Y | X or Y | X xor Y |
| 0 | 0 | 0 | 0 | 0 |
| 0 | 1 | 0 | 1 | 1 |
| 1 | 0 | 0 | 1 | 1 |
| 1 | 1 | 1 | 1 | 0 |
如果通过坐标来展示,则如下图所示:
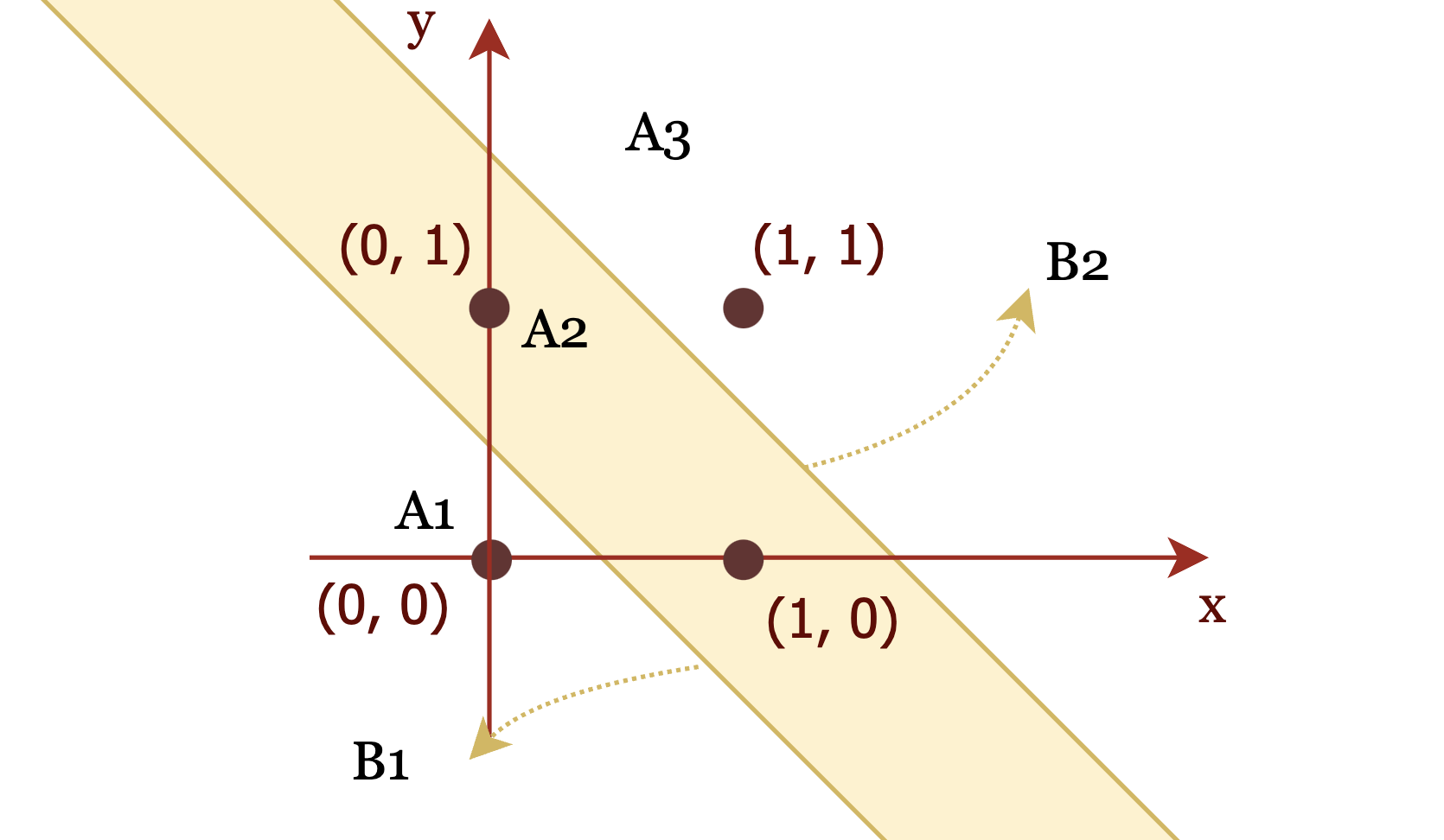
通过两个边界和
将二维平面分割成三个区域
、
和
。则
操作意味着拟合
,就可以对这四个点进行正确分类;
操作意味着拟合
;但
意味着线性函数需要同时拟合
和
,这在逻辑上是不可能的。
那如何通过神经网络实现操作呢?答案是需要加深神经网络的深度:
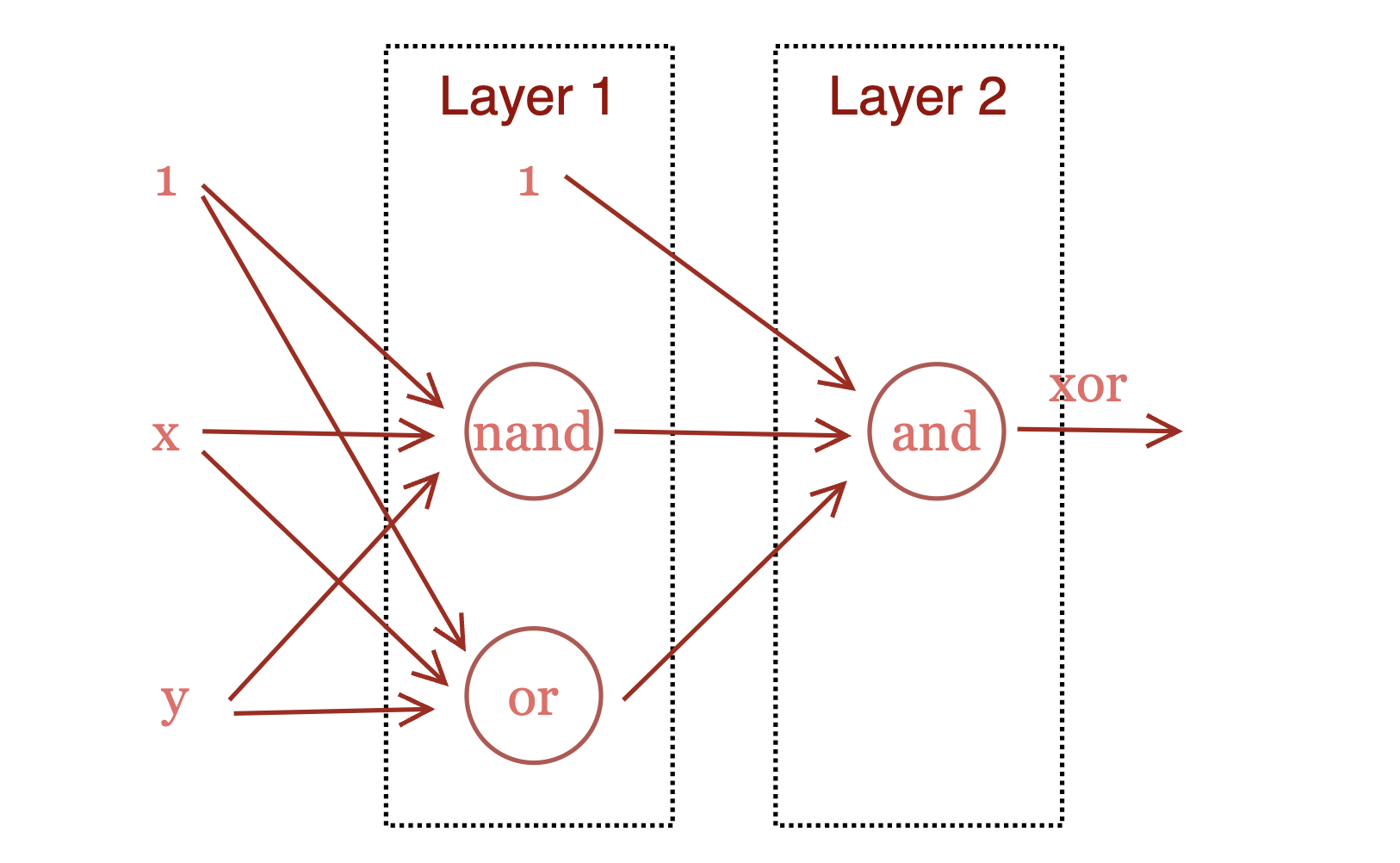
真值表见下:
| X | Y | X or Y | X nand Y | X xor Y = (X or Y) and (X nand Y) |
| 0 | 0 | 0 | 1 | 0 |
| 0 | 1 | 1 | 1 | 1 |
| 1 | 0 | 1 | 1 | 1 |
| 1 | 1 | 1 | 0 | 0 |
4.2 《感知机:计算几何学引论》
线性分类特性成了单层感知机致命的硬伤,正是因为单层感知机无法解决非线性分类问题,最终导致了对感知机的研究戛然而止,神经网络的发展趋势急转直下。
1969年,由马文·明斯基(Marvin Minsky)和西摩·佩珀特(Seymour Papert)共同编著的著作《感知机:计算几何学引论》正式出版。该书为感知机建立了完善的数学理论并给出了理论证明,同时确定了感知机的能力边界。明斯基在书中提到了前面所说的问题,指出弗兰克·罗森布拉特的感知机解决不了该类问题。

弗兰克·罗森布拉特其实早已知道单层感知机的缺陷,并在探索多层感知机,但苦于无法设计出一种方法可以保证多层感知机训练时一定收敛,且也不具备明斯基的数学天赋,证明多层感知机的收敛特性,致使其观点在学术界难以流行,再加上同年的另外一件事:
Minsky won the Turing Award (the greatest distinction in computer science)[40] in 1969.
明斯基于1969年荣获图灵奖(计算机科学最高奖项)
这在学术界,彻底扭转了人工智能的研究方向,人工智能从连接主义转向符号主义,神经网络成了一个不受欢迎的代名词。
- Connectionism (coined by Edward Thorndike in the 1930s) is a name of an approach to the study of human mental processes and cognition that utilizes mathematical models known as connectionist networks or artificial neural networks.[1] Connectionism has had many 'waves' along the time since its beginnings.
- 连接主义(由爱德华·桑代克在20世纪30年代首创)是一种研究人类精神过程和认知的方法,它利用被称为连接主义网络或人工神经网络的数学模型。
- Symbolic AI is a subfield of AI that deals with the manipulation of symbols. Symbolic AI algorithms are designed to solve problems by reasoning about symbols and relationships between symbols.
- 符号主义使用符号构建人类知识,并在上面基于推理规则和知识间关系来实现人工智能。
马文·明斯基具有很强的数学能力,所以他在看透单层感知机的底层数学原理后,对单层感知机能实现人工智能产生了强烈的怀疑。在上个世纪六十年代,计算机的计算性能远远不够,完全不存在像GPT-4这种大力出奇迹的产物。在学术界也没有理论证实在神经网络规模到达一定程度后,会涌现(unlock)出智能的各种表现。那时的马文·明斯基坚信,单靠神经元是无法实现智能的,人类智能的存在一定有其他更高层次的表达形式。所以他坚定地支持符号主义,并凭一己之力扭转了人工智能的研究方向。
番外:弗兰克·罗森布拉特是康奈尔大学的教授,马文·明斯基是麻省理工大学的教授,而当时康纳尔大学远比麻省理工更出名。然而,更具戏剧性的是弗兰克·罗森布拉特和马文·明斯基都在朗克斯科学高中读的高中,弗兰克比马文高一届。可以说正是学弟亲手终结了学长的研究生涯。
马文·明斯基,这位人工智能之父,在1956年创立人工智能之后,又在1969年亲自判处了神经网络的死刑。从神经网络的视角来看,这是真正的成也萧何,败也萧何!
4.3 多层神经网络的拟合能力
到这里,我们需要回答一个问题:神经网络可表达能力的极限在哪里?感知机只能处理线性分类的致命缺点能否被克服呢?
在数学上,如果我们有两个函数和
,如果
和
都是线性函数,则无论是
还是
都依然是线性函数。
如果我们将和
当做两个神经元的数学表示,那么
和
便代表了神经元连接的两种形式(区别仅在于谁连接谁)。换言之,假设
和
是单层神经网络,那么
和
便是二层神经网络。
那多层神经网络究竟是如何增强自己的表达能力的呢?答案是激活函数,因为在神经元的数学模型中,除了线性部分的累和之外,还有非线性部分的激活函数。
事实上,在神经元足够多的前提下,二层神经网络就可以拟合任意函数。我们下面不会给出严格的数学证明,但会给一个更为直观的解释,便于大家理解。
首先,我们考虑单输入、单输出的场景,即,其中的
是标量,
也是标量。假设函数图像如下所示:
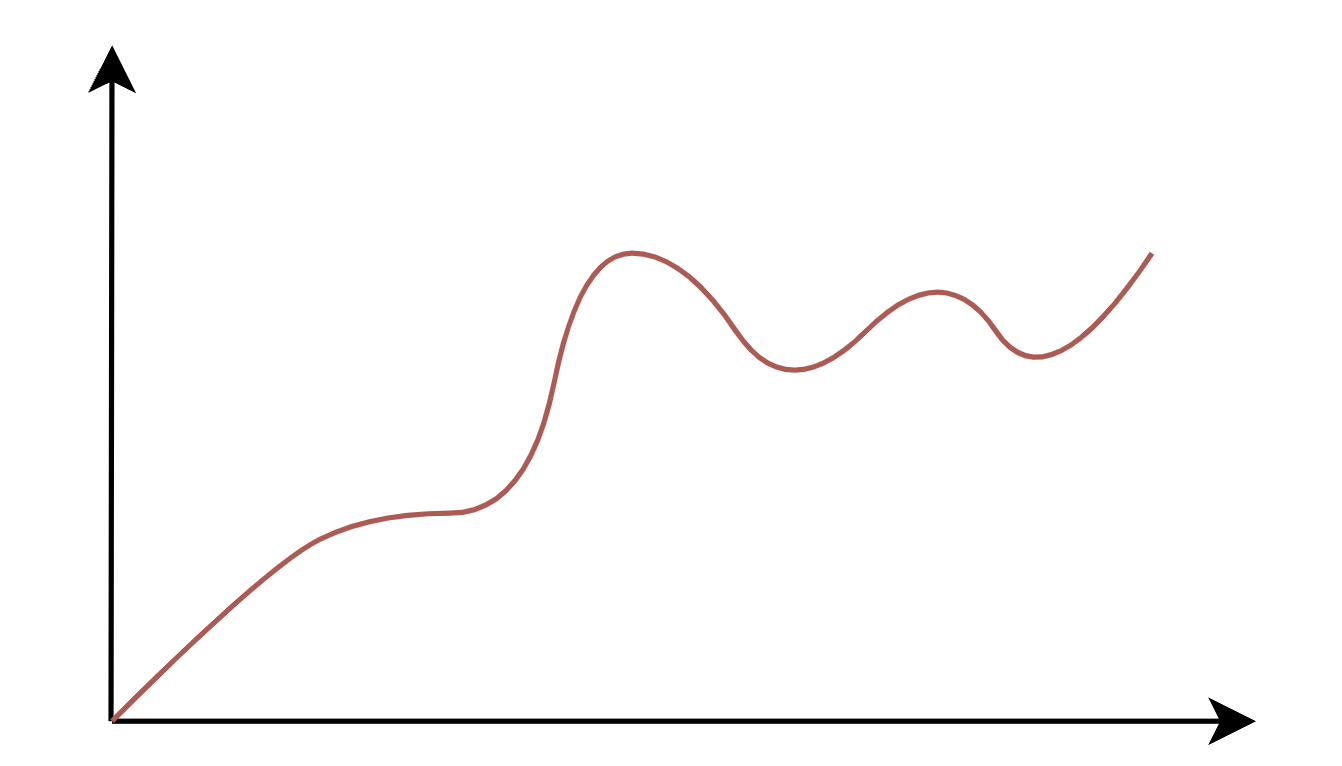
需要拟合的函数曲线
我们使用下图所示的双层神经网络来拟合上面的曲线:
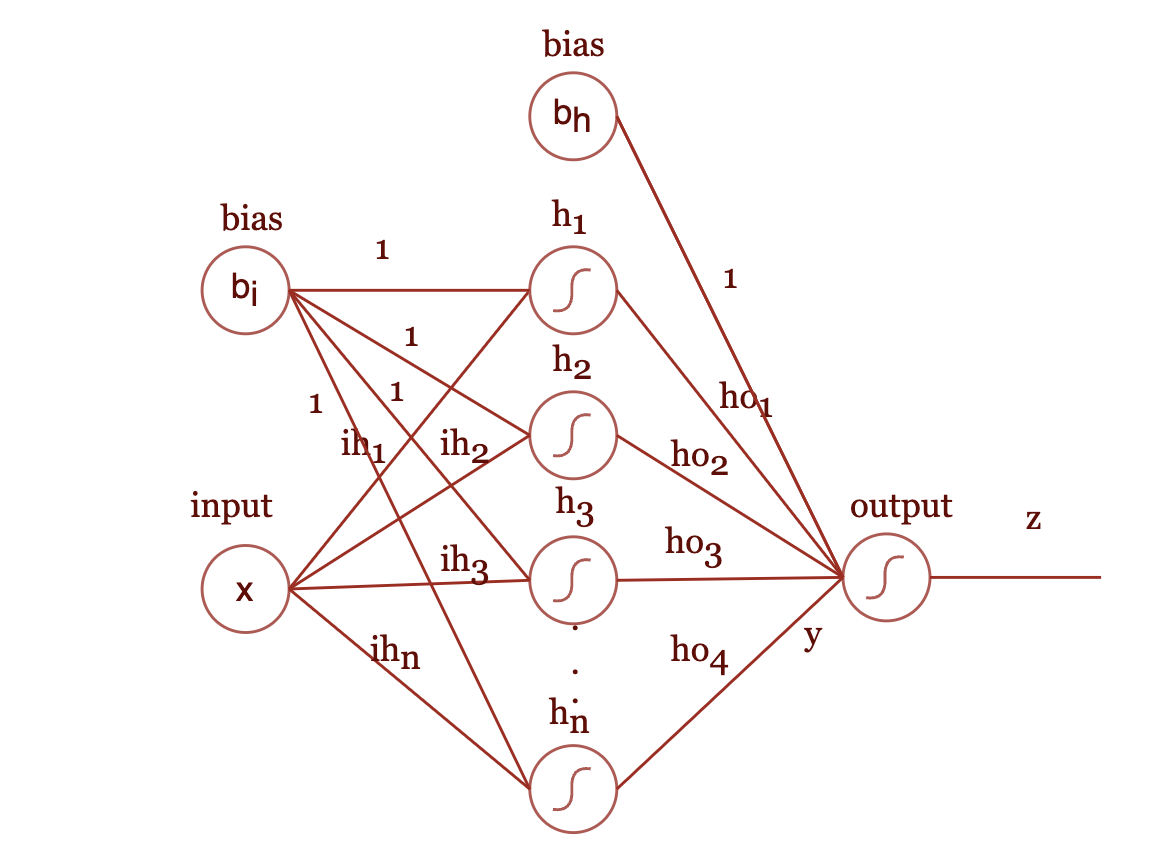
双层神经网络
激活函数我们选择最简单的形式:
我们先考虑输出神经元,其输出
和输入
之间的函数关系便是
。
神经元输出的具体形式会根据实际使用场景来设置,如果是二分类问题,则可以将设置为输出
之间的实数,表示输入
是
的概率大小。所以要考量双层神经元的拟合能力,我们仅需看原始输入
到
的输入
能否拟合任意函数曲线即可。
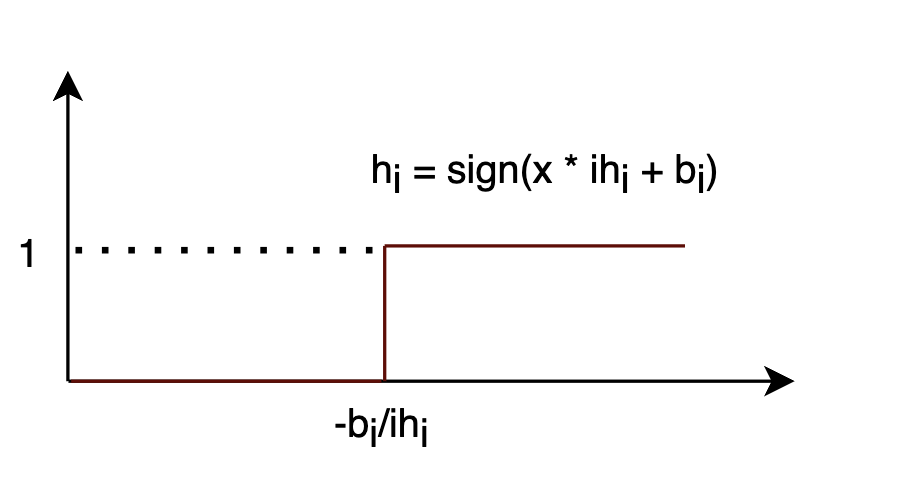
考虑和隐藏层输出之间的关系:
现在考虑和输入
之间的关系:
绘制出该函数的图像,我们可以通过调整的值,来控制函数发生跳变的位置:
考虑整体的整体函数:
则的结果依赖于
的累和,我们可以通过设置
来控制
跳变的位置,通过设置
来控制跳变的幅度和方向(
则让
值变大,反之则让
值变小)。
则在最开始的给出的曲线函数,可以拟合成如下的图形

当我们增加神经元数量,调整模型中的相关参数,则可以使模型的输出无线接近目标函数。
上面就是对两层神经网络的拟合能力的直观解释。
上世纪六十年的学术界,难道不知道神经网络的拟合能力吗?很多资料都表明,在当时学术界已经知道双层神经网络的拟合能力是可以无限逼近任何曲线了。但理论上知道,和实际上能落地应用之间存在着巨大的GAP。在当年,这个GAP主要是计算和存储能力。它成了不可逾越的鸿沟,也直接导致了神经网络研究的第一次低谷。
5. 复兴:反向传播算法、CNN、AlexNet
在神经网络研究遇冷的年代里,依旧有着部分的学者坚信神经网络才是AI的未来,在之后的很长时间里,虽进展缓慢,但却并未彻底消亡。其中不得不提的人物,一定是杰弗·辛顿(Geoffery Hinton)。
Geoffrey Everest Hinton CC FRS FRSC(born 6 December 1947) is a British-Canadian cognitive psychologist and computer scientist, most noted for his work on artificial neural networks. From 2013 to 2023, he divided his time working for Google (Google Brain) and the University of Toronto, before publicly announcing his departure from Google in May 2023 citing concerns about the risks of artificial intelligence (AI) technology. In 2017, he co-founded and became the chief scientific advisor of the Vector Institute in Toronto.
杰弗里·埃弗雷斯特·辛顿 CC FRS FRSC(1947年12月6日出生)是一位英国-加拿大认知心理学家和计算机科学家,他在人工神经网络方面的工作最为人所知。从2013年到2023年,他在谷歌(Google Brain)和多伦多大学之间分配了他的工作时间,直到2023年5月他公开宣布因对人工智能(AI)技术风险的担忧而离开谷歌。2017年,他共同创立并成为多伦多Vector研究所的首席科学顾问。
也许这样介绍还无法让读者意识到杰弗·辛顿对神经网络发展的贡献,那就补一张杰弗·辛顿的“朋友圈”:
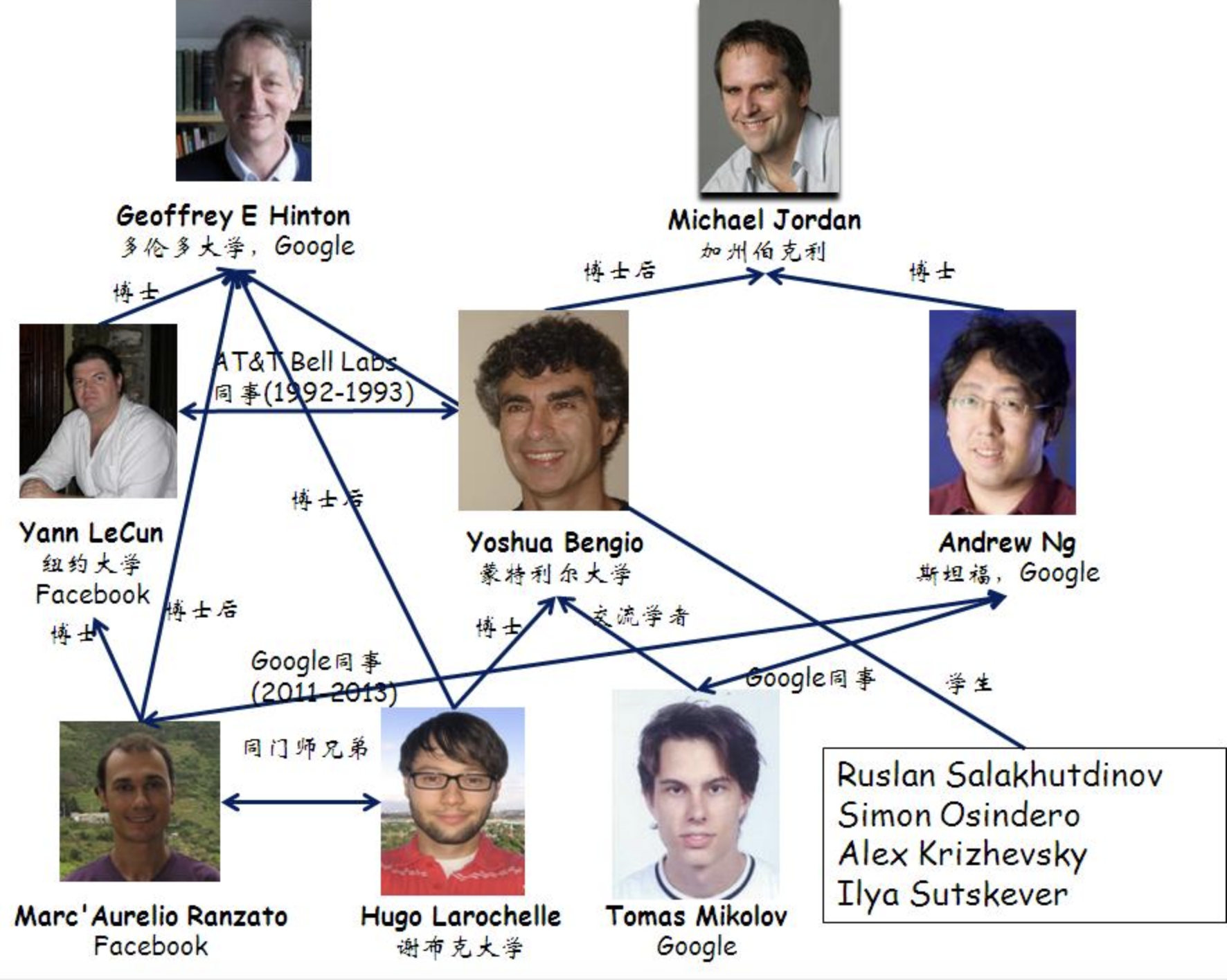
5.1 反向传播算法
1986年,大卫·鲁梅尔哈特(David Rumelhart)、杰弗·辛顿(Geoffery Hinton)和罗纳德·威廉姆斯(Ronald J. Williams)共同发表了一篇名为《Learning representations by back-propagating errors》的论文,反向传播算法正式登上人工智能发展的历史舞台。从谷歌学术上搜索看,这篇文章目前的引用量为34629次,由此可见反向传播算法对人工智能发展的重要程度。

反向传播算法是梯度下降算法和微分链式法则的融合,通过微分的链式法则,将训练误差从输出层逐层传导到输入层,分层计算每层的微分,再通过梯度下降的方式,让整个神经网络向着收敛的方向训练。
我们用一个简单的例子来说说明,反向传播算法的计算过程。
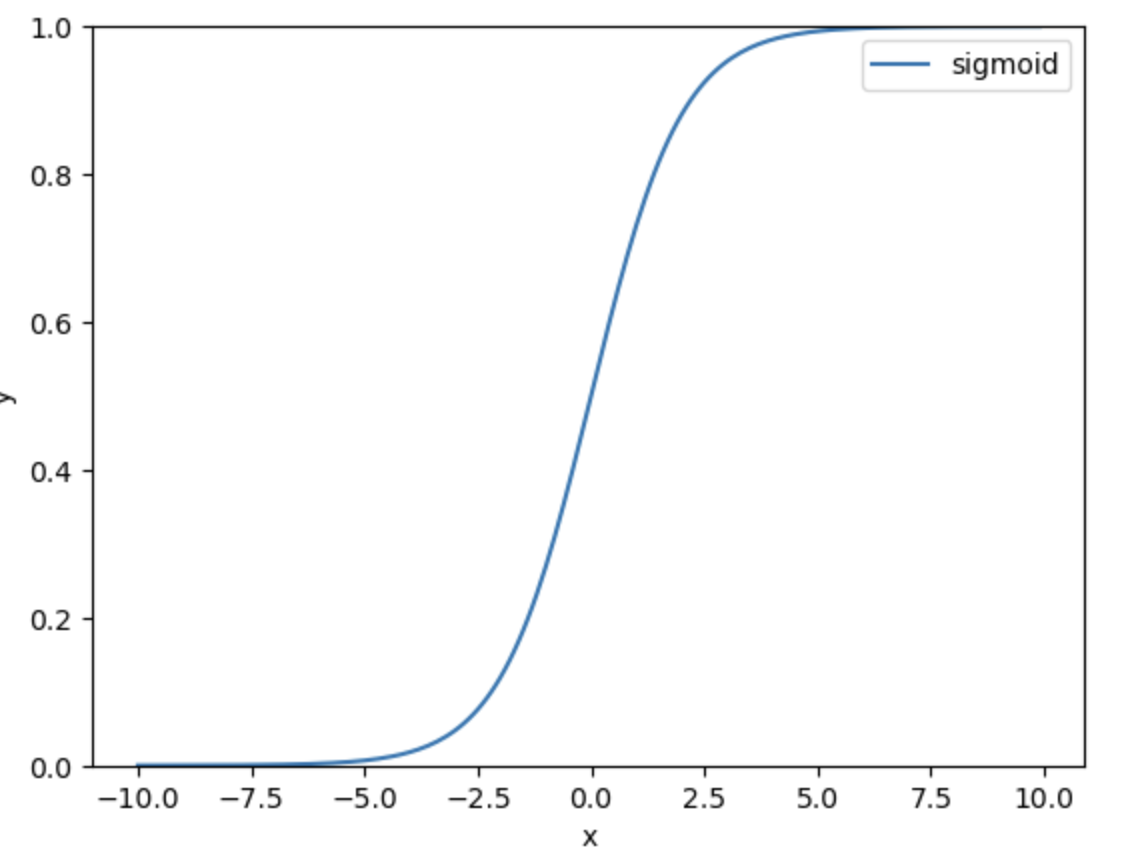
首先,我们引入一个新的激活函数,函数:
它的图形如下图所示:
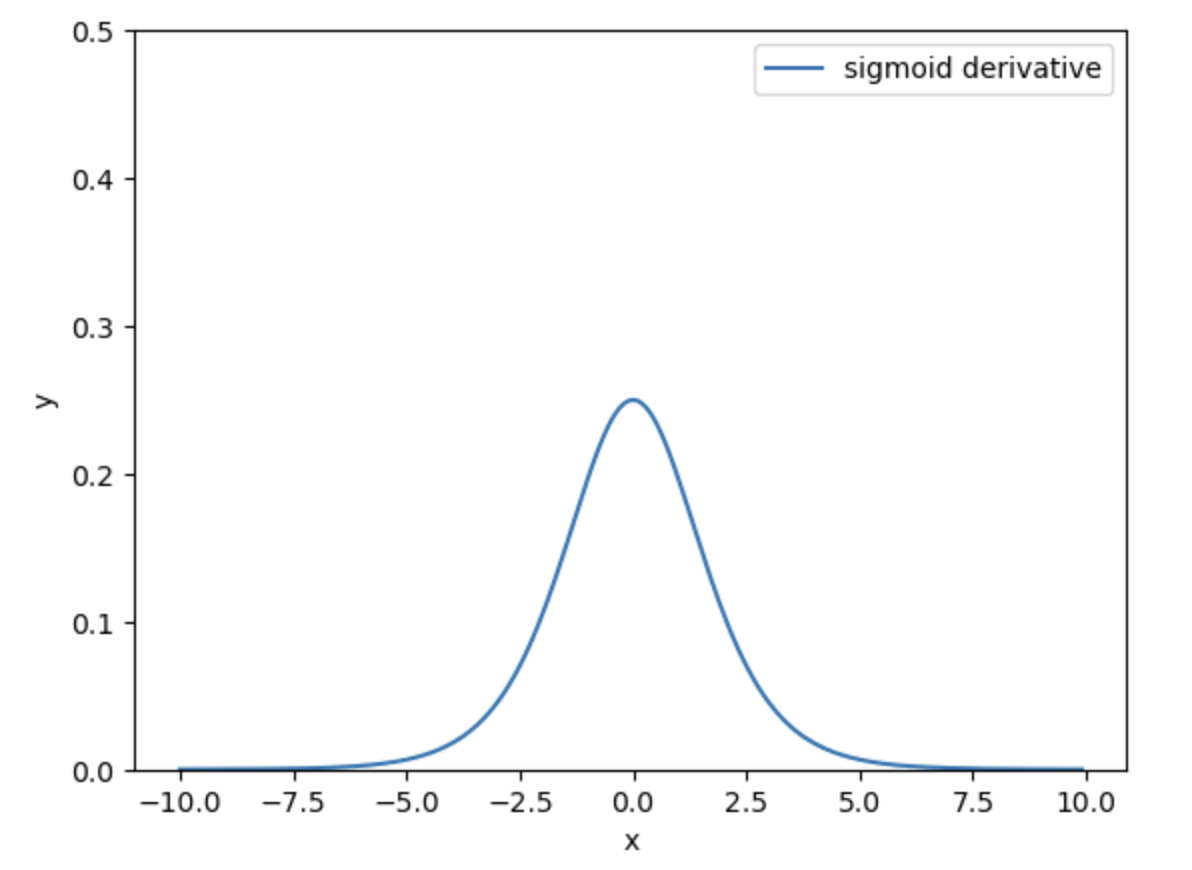
函数的一阶导数形式如下:
它的图形如下所示:
我们先构造一个简单的神经网络,如下图:

由于偏置单元的导数是,为了介绍简便起见,我们将神经网络中的偏置单元直接隐去。
每个神经元都对应一个输入和输出,我们使用表示第
个神经元的输入,用
表示第
个神经元的输出。
在机器学习中,学习的目标是通过调整参数,尽可能降低损失函数的值,也就是求取损失函数的全局最小值。损失函数是用来定义模型预测结果和目标值之间的差异,损失函数越小则差异越小,预测结果越精确。
神经网络的损失函数可以通过均方误差函数来定义:
由于机器学习算法是在给定输入、输出的前提下,优化参数,因此在优化过程中,变量是参数,梯度下降算法是对参数求导,找到损失函数下降最快的方向,来调整参数的取值。
因此,反向传播算法本身在运用链式法则时,是将损失函数在参数维度上求偏微分。
我们根据上图,给出几个例子:
- 损失函数对
的偏导:
汇总起来,损失函数对$w_5$的偏导的计算公式为:
- 损失函数对
的偏导,推导过程和上面类似,不过层级会更深一点,最后的计算公式为:
5.2 梯度消失和梯度爆炸
梯度爆炸在神经网络学习过程中出现的概率不大,我们主要来讨论梯度消失的情况。
在上面公式中可以看到很多类似的因子,这个是
的导数形式。
的导数从前面给出的函数曲线可以看到,这个函数最大值也仅是
。
神经网络层级越深,反向传播算法从后往前计算偏微分时,累积计算的的导数的次数便会越多,这会导致深层神经网络的前几层的导数值非常小。越往前的神经元,就越难学习到有用的特征,越难以收敛,这便是梯度消失的问题。
解决梯度消失的问题的一个有效方法,是找到其他替代的激活函数。这些替代的激活函数,在反向传播过程中,不会显著降低梯度(这要求这些激活函数的导数不能太小,最好接近于1)。
下面是其他几个激活函数的函数曲线和其导数的函数曲线:
函数
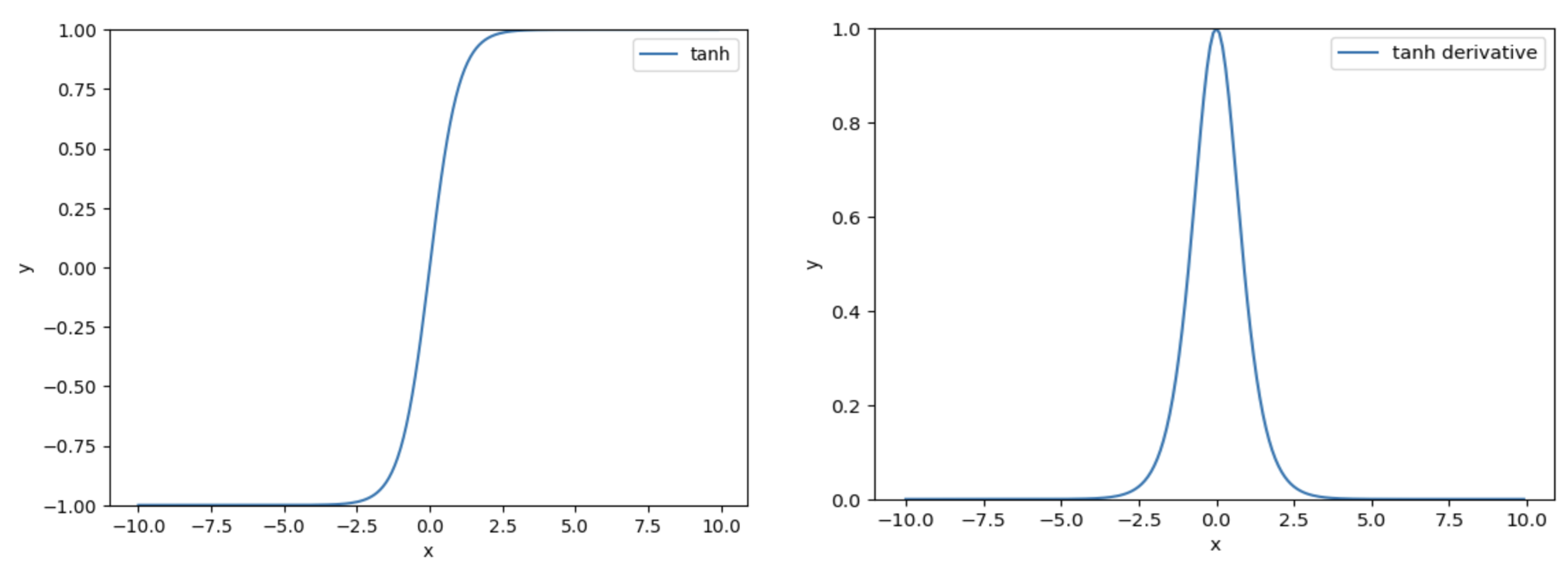
-
函数
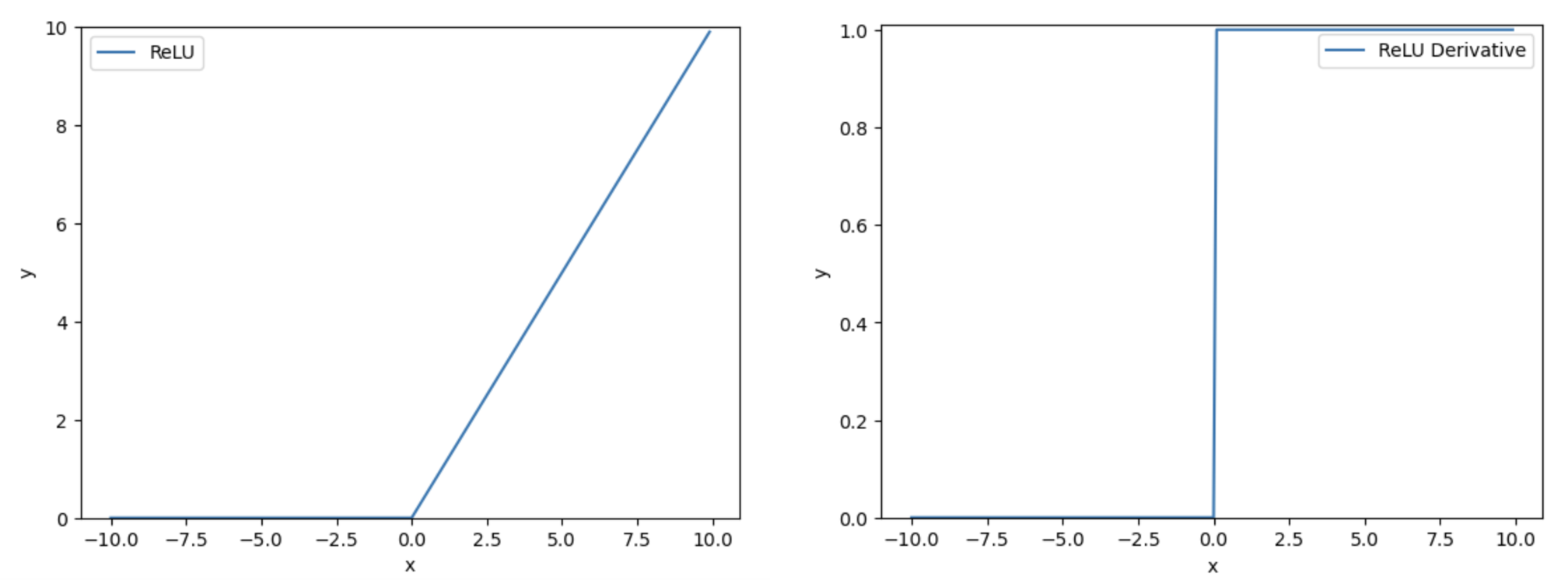
还有一些其他的激活函数,不一一枚举了,感兴趣可以看下参考文献。
5.3 ALVINN - 基于神经网络的自动驾驶系统
1987年,迪安·波默洛(Dean Pomerleau)使用神经网络重构了卡耐基·梅隆人工智能实验室正在研制的自动驾驶卡车的核心代码,他将这个系统命名为ALVINN(An Autonomous Land Vehicle In A Neural Network)。
该项目之前通过编写卡车行驶过程中遇到各类情况下的详细指令,试图创造出一台可以自动驾驶的卡车。项目启动几年之后,在当年秋天,这辆车行驶的速度达到了有每秒几英寸(1英寸 = 2.54厘米)。
使用ALVINN之后,卡车通过观察人类的驾驶行为来学会如何驾驶,通过分析人类在直道、转弯出的行为,很快便能够在申利公园进行自动驾驶。
ALVINN训练和自动驾驶的视频:https://twitter.com/i/status/1335956191088959488
1991年春天,ALVINN以接近60英里的时速从匹兹堡开到宾夕法尼亚州的伊利市。在明斯基和佩珀特的《感知机》一书出版20多年后,ALVINN做到了他们说神经网络做不到的事情。
1988年的一篇名为《Alvinn: An autonomous land vehicle in a neural network》论文中,迪安·波默洛给出了ALVINN的系统架构:
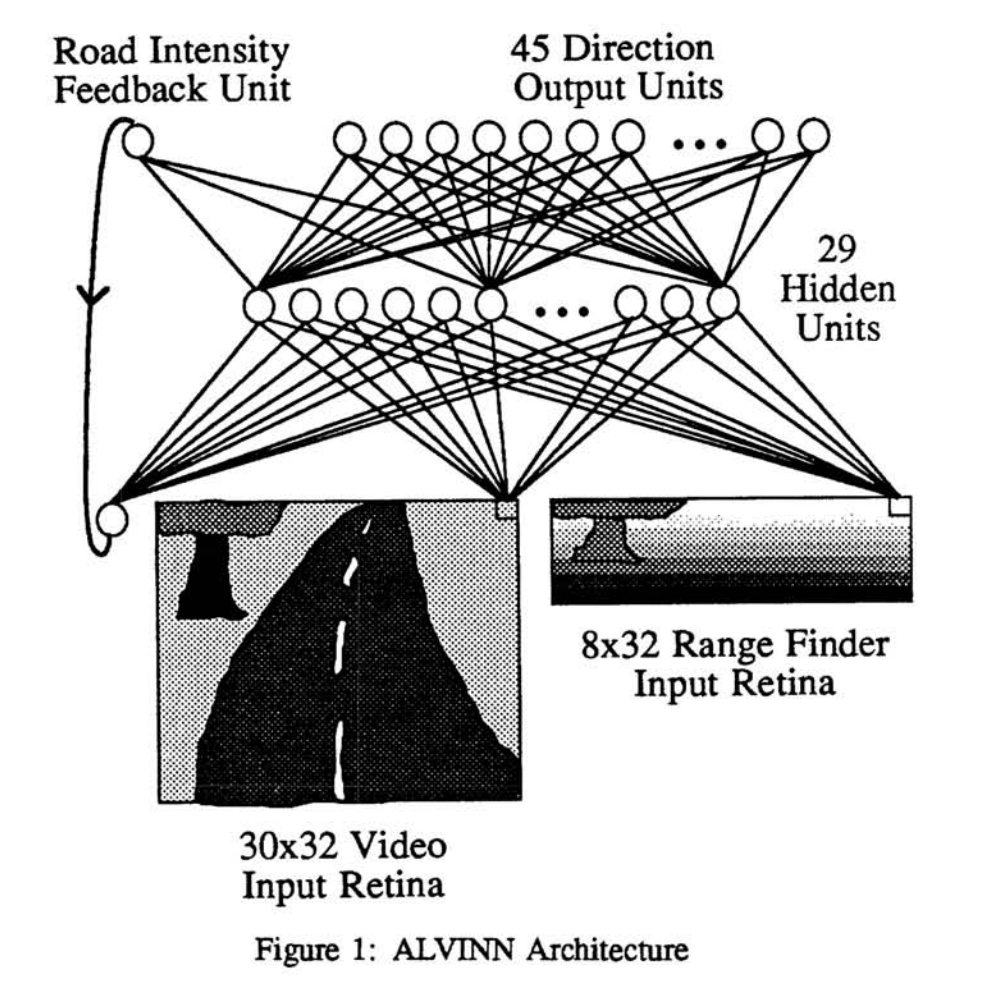
5.4 CNN网络
杨立昆坐在台式电脑前,穿着一件白衬衣,外面套着深蓝色的毛衣。那是1989年,当时台式电脑仍然靠电线连接着微波炉大小的显示器,并配有旋钮来调节屏幕颜色和亮度。另一根电线从这台机器的后部延伸到一个看起来像是倒挂的台灯的东西,但那不是台灯,而是一部摄像机。左撇子杨立昆会心一笑,用左手拿起一张纸条,上面有个手写的电话号码201—949—4038,他把纸条放到摄像机下面。这时,纸条的影像出现在了显示器屏幕上。当他敲击键盘时,屏幕顶部出现了一道闪光,这是一个快速计算的提示,几秒之后,机器读取了纸条上的内容,并以数字化的形式显示出相同的数字:201—949—4038。
这个是youtube上记录下来的视频:https://www.youtube.com/watch?v=FwFduRA_L6Q
杨立昆(Yann LeCun)曾在多伦多大学跟随辛顿做了一年的博士后研究,那个可以识别摄像机拍摄数字的系统叫LeNet,这是一个以杨立昆命名的神经网络,这个神经网络将卷积计算和神经网络相结合,被称之为卷积神经网络(CNN,Convolutional Nerual Network)。而杨立昆,则被称为卷积神经网络之父。
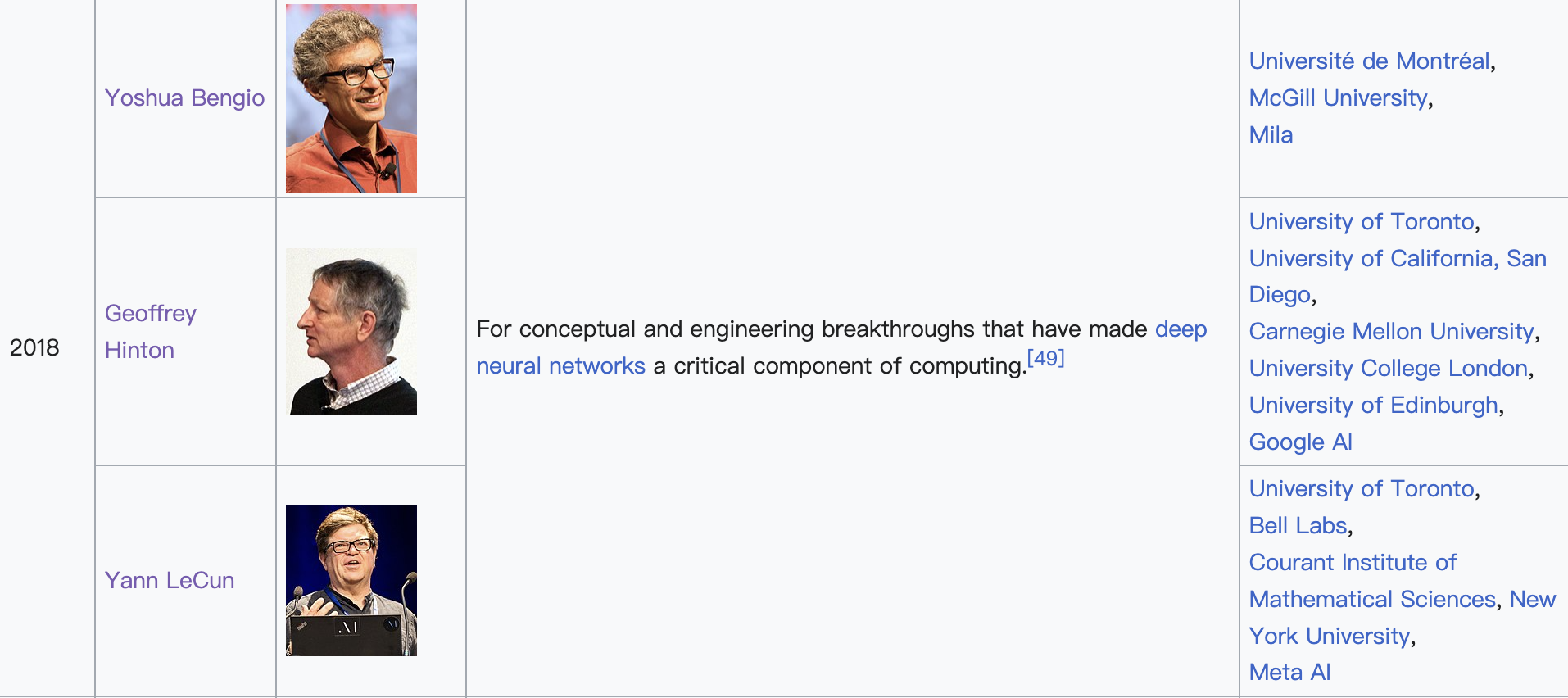
另外,杨立昆也是一位图灵奖获得者:
2019年3月27日,美国计算机协会(ACM)宣布把2018年的图灵奖(Turing Award)颁给人工智能科学家Yoshua Bengio(约书亚·本吉奥),Geoffrey Hinton(杰弗里·辛顿)和Yann LeCun(杨立昆),以表彰他们为当前人工智能的繁荣发展所奠定的基础。
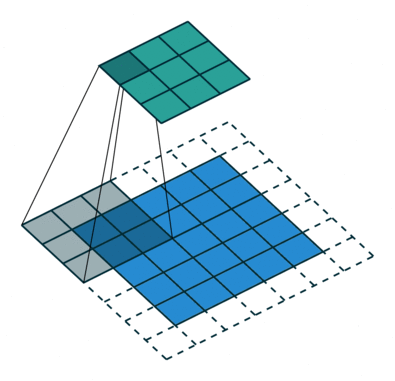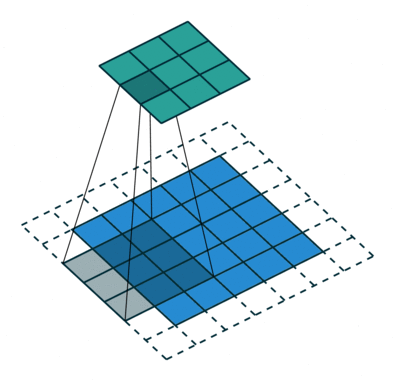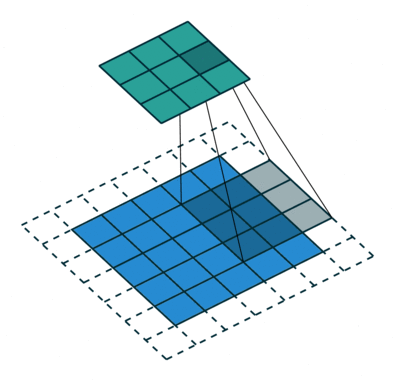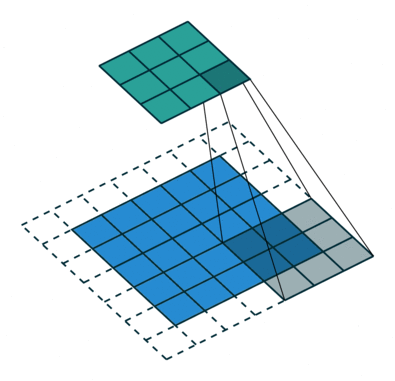
卷积神经网络是数字图像处理和神经网络相结合的产物。如何让机器识别图像内容,一直是人工智能领域长期探索的课题。卷积可以通过设置合适的卷积核,在以像素组成的数字图像中,通过卷积函数的滤波特性,提取出诸如边界、形状等可以帮助识别图像内容的有用特征。再此基础上,结合神经网络的学习能力,便可以让卷积神经网络具备从图像中学习分辨目标物体的能力,这便是设计卷积神经网络的核心逻辑。下图是通过一个通过一个$3 \times 3$的卷积核,在一个二维图像中计算卷积的动态展示:
下图是在1998年发表的《Gradient-based learning applied to document recognition》论文中,给出的LeNet的架构:
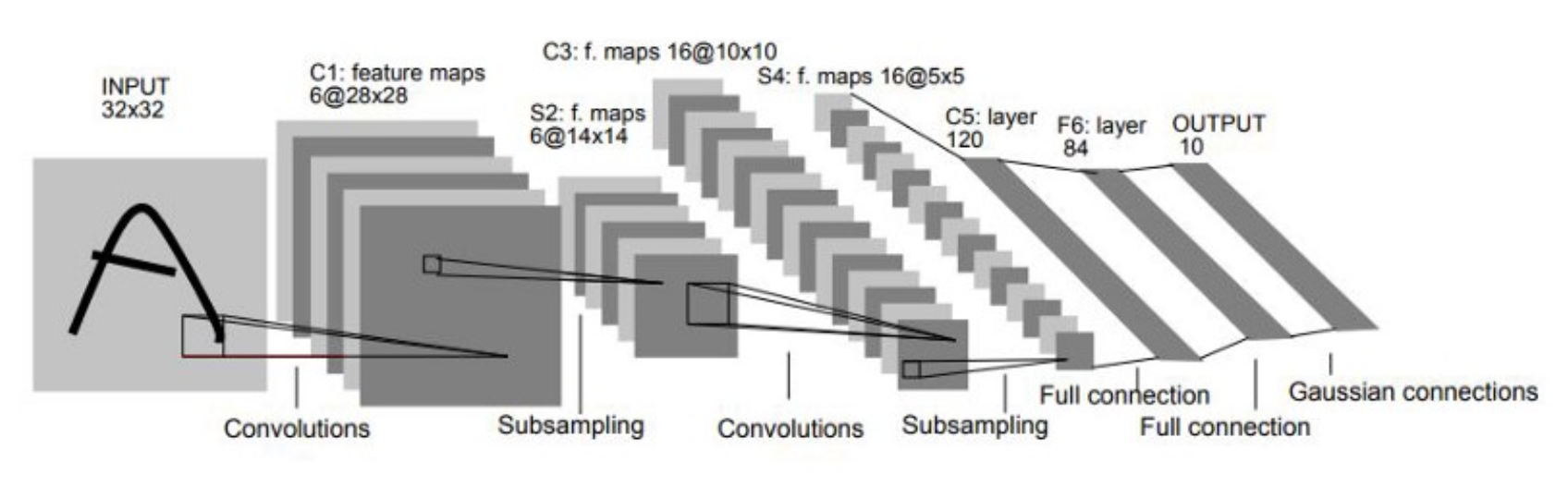
LeNet的模型架构
5.5 AlexNet
如果说辛顿的反向传播算法,让神经网络再次进入大众视野的话,那么下面这篇论文,则是让神经网络再次大火的源头。2012年,由亚历克斯·克里泽夫斯基(Alex Krizhevsky)、伊利亚·萨特斯基弗(Ilya Sutskever)、杰弗里·辛顿(Geoffrey E. Hinton)发表了《ImageNet Classification with Deep Convolutional Neural Networks》。
亚历克斯·克里泽夫斯基和伊利亚·萨特斯基弗是杰弗·辛顿的学生,这篇文章的引用量超过了十万次:

这篇文章详细介绍了在当年的ImageNet竞赛中赢得冠军CNN模型的架构,包括改模型相关的超参数配置:
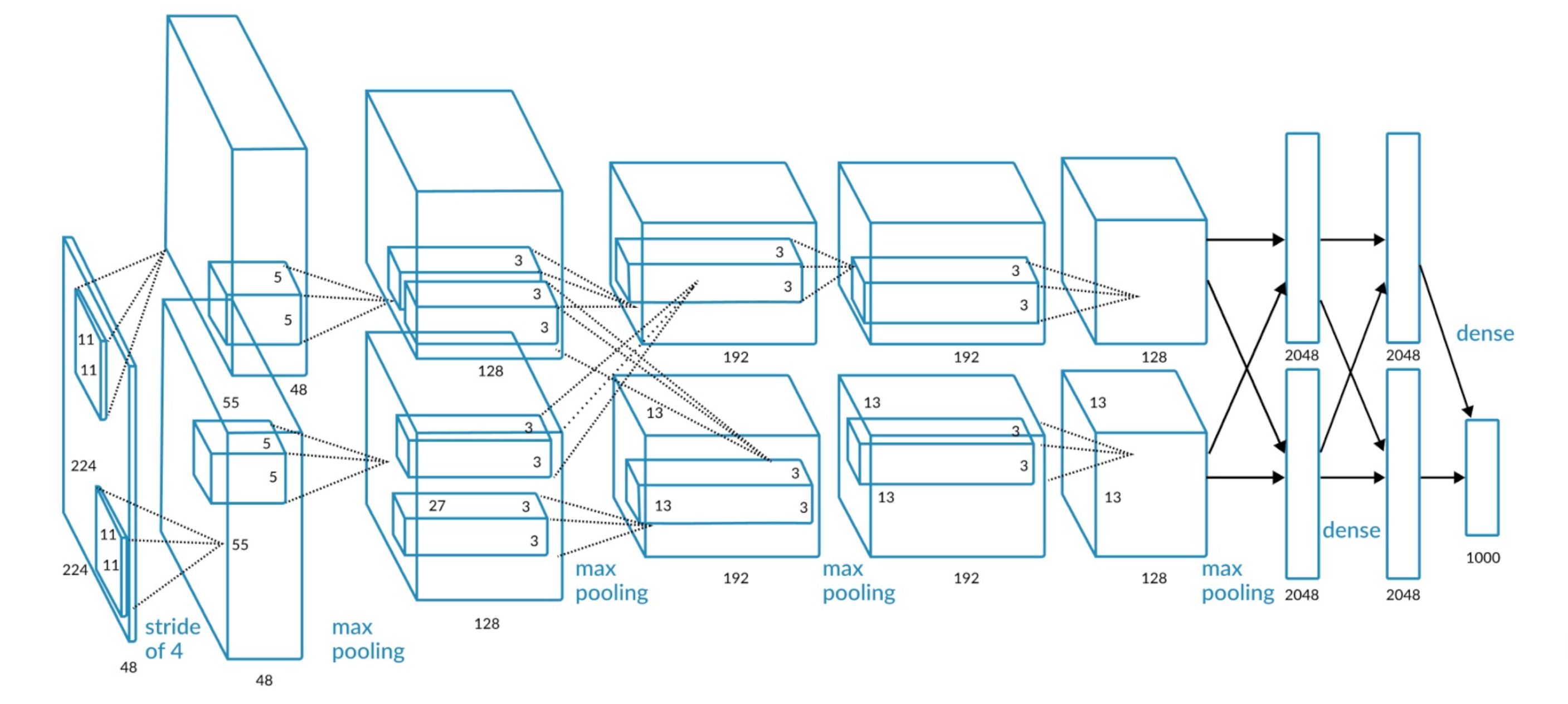
AlexNet模型架构
该模型的参数量见下表(总计6千万+参数):
| Input | Layer | Stride/Pad | Kernel Size | Output | # of Params |
| 227 * 227 * 3 | conv1 | 4/0 | 96 * 11 * 11 * 3 | 55 * 55 * 96 | 34944 |
| 55 * 55 * 96 | maxpool1 | 2/0 | 96 * 3 * 3 * 96 | 27 * 27 * 96 | 0 |
| 27 * 27 * 96 | conv2 | 1/2 | 256 * 5 * 5 * 96 | 27 * 27 * 256 | 614656 |
| 27 * 27 * 256 | maxpool2 | 2/0 | 256 * 3 * 3 * 256 | 13 * 13 * 256 | 0 |
| 13 * 13 * 256 | conv3 | 1/1 | 384 * 3 * 3 * 256 | 13 * 13 * 384 | 885120 |
| 13 * 13 * 384 | conv4 | 1/1 | 384 * 3 * 3 * 384 | 13 * 13 * 384 | 1327488 |
| 13 * 13 * 384 | conv5 | 1/1 | 256 * 3 * 3 * 384 | 13 * 13 * 256 | 884992 |
| 13 * 13 * 256 | maxpool5 | 2/0 | 256 * 3 * 3 * 256 | 6 * 6 * 256 | 0 |
| 6 * 6 * 256 | fc6 | 0/0 | 4096 * 6 * 6 * 256 | 1 * 1 * 4096 | 37753832 |
| 1 * 1 * 4096 | fc7 | 0/0 | 4096 * 1 * 1 * 4096 | 1 * 1 * 4096 | 16781312 |
| 1 * 1 * 4096 | fc8 | 0/0 | 1000 * 1 * 1 * 4096 | 1 * 1 * 1000 | 409700 |
| Total | 62,378,344 | ||||
该模型在当年的TOP-5的错误率是15.3%,夸张的是比第二名低了10.8个百分点(翻译过来就是:我错误率是十几个pt,但我比第二低了十几个pt。这种表述听着就挺离谱)。
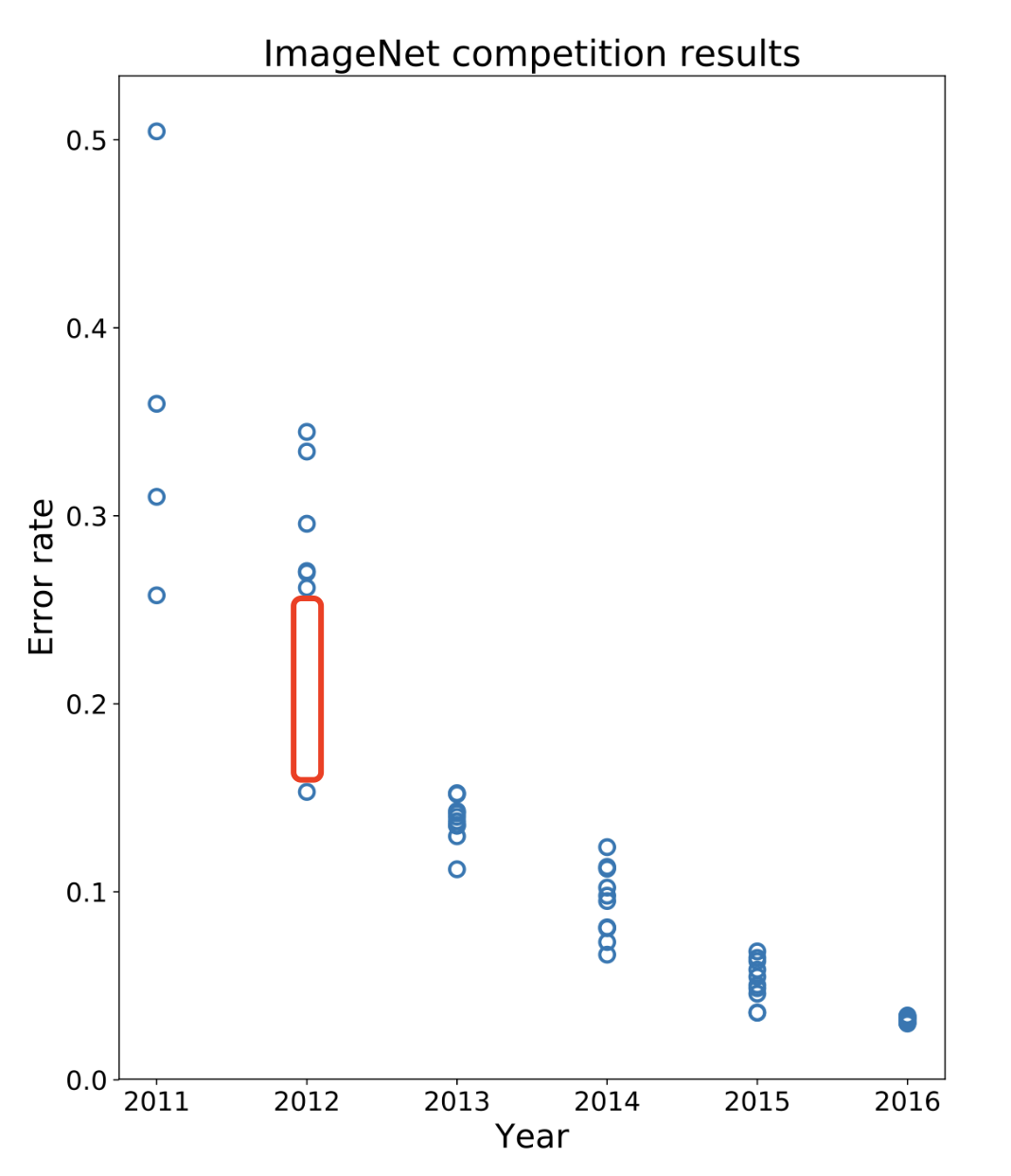
历年ILSVRC的错误率分布
6. 高潮:DeepMind、OpenAI
6.1 DNNresearch
2012年ILSVRC惨遭AlexNet屠榜之后,无论是学术界还是企业界,都意识到了神经网络的巨大潜力,互联网巨头们纷纷开始招募学术界在神经网络领域的专家。新一轮的军备竞赛,开始了。
首先,包括百度、谷歌、微软都对AlexNet的作者抛出了橄榄枝,而辛顿他们也需要更多的资金支持进一步研究。因此,在当年辛顿和他的两位学生,创办了一家名为DNNresearch的公司,这家公司没有任何产品,只有三个员工:亚历克斯·克里泽夫斯基、伊利亚·苏茨凯弗、杰弗里·辛顿。
成立这家公司的唯一目的,就是为了让互联网巨头,通过竞标的方式收购这家公司,其实说白了就是招募亚历克斯·克里泽夫斯基、伊利亚·苏茨凯弗、杰弗里·辛顿三位神经网络领域大佬。参与这次竞拍的公司有谷歌、微软、百度、DeepMind,最终谷歌出价4400万美元,完成了对这家公司的收购。
6.2 Google Brain & DeepMind
2011年,吴恩达(Andrew Ng)加入谷歌,同杰弗·迪恩(Jeff Dean)、格雷科拉多(Greg Corrado)一起,参与一项斯坦福大学和谷歌公司的联合项目,他们在当年联手创造了一个大型深度学习软件平台DistBelief。通过该平台,谷歌使用由16000个电脑组成的人工神经网络分析Youtube上关于猫的资料,最终训练出了可以识别猫的神经网络模型。
2012年,基于上述研究,谷歌发表了一篇俗称小猫论文的论文:《Building High-level Features Using Large Scale Unsupervised Learning》。
由于该项目取得了惊人的效益和成功,便从Goolge X中独立拆分出来,成立了单独的部门,这个部门就是谷歌大脑(Google Brain)。
吴恩达后来从Google Brain离职,去了百度。
而DeepMind的成立时间,比吴恩达进入谷歌的时间还要早。DeepMind是2010年由德米斯·哈萨比斯(Demis Hassabis)、肖恩·莱格(Shane Legg)和穆斯塔法·苏莱曼(Mustafa Suleyman)等人在伦敦成立的一家AI研究机构。
2014年,谷歌正式宣布以6.5亿美元收购DeepMind,彼时DeepMind总计仅有50名员工(结合前面收购DNNresearch的案例,可以想象当年深度学习领域的军备竞赛究竟是多么的不计成本)。
这起收购,有两条附加条件一直被大家广泛讨论(赞扬的一派认为这体现了创始者的操守,而否定的一派觉得这只是为了抬升收购价格):
哈萨比斯要求谷歌禁止将DeepMind技术用于军事目的;
坚持要求谷歌设立一个独立的道德委员会,监督DeepMind通用人工智能技术的使用;
德米斯·哈萨比斯的人生经历充分诠释了什么是天才:
4岁对国际象棋产生兴趣,5岁参加英国国内比赛,6岁赢得伦敦8岁以下竞标赛冠军,9岁成为当时世界第二的英国11岁以下国家队队长,13岁成为该年龄段的世界第二象棋大师;
14岁提前两年完成类似中国中考的考试CGSE,15岁时数学水平达到A level,16岁时,高等数学、物理和化学均达到A level,当年考入剑桥大学计算机科学专业,因为年龄太小,剑桥建议他休学一年
17岁,开发游戏ThemePark,这款游戏销售破百万份
20岁,哈萨比斯以极为少见的双重一级荣誉学位(double first-class honours degress)从剑桥皇后学校毕业;
20岁,创立游戏公司Elixir,估值最高达1200万英镑;当公司大火时,哈萨比斯觉得自己的知识不够用,便回学校读书去了。
21岁,参加英国全能脑力比赛,赢得冠军;在接下来的五年里,他又赢了四次。另外一次,是他没参加。

DeepMind最为大众所熟知且津津乐道的事件,则非AlphaGo莫属了:
- 2015年10月,AlphaGo在一场闭门比赛中,击败了三届欧洲围棋冠军范辉
- 2016年3月,AlphaGo以4-1的比分击败了韩国九段围棋大师李世石
- 2017年5月,AlphaGo以3-0的比分击败了当时的世界第一围棋大师柯洁
至此,在围棋领域,AI已经远远超过了人类的智能极限。一直认为因规则过于复杂,AI不可能战胜人类的围棋,也在深蓝事件之后,彻底沦陷……
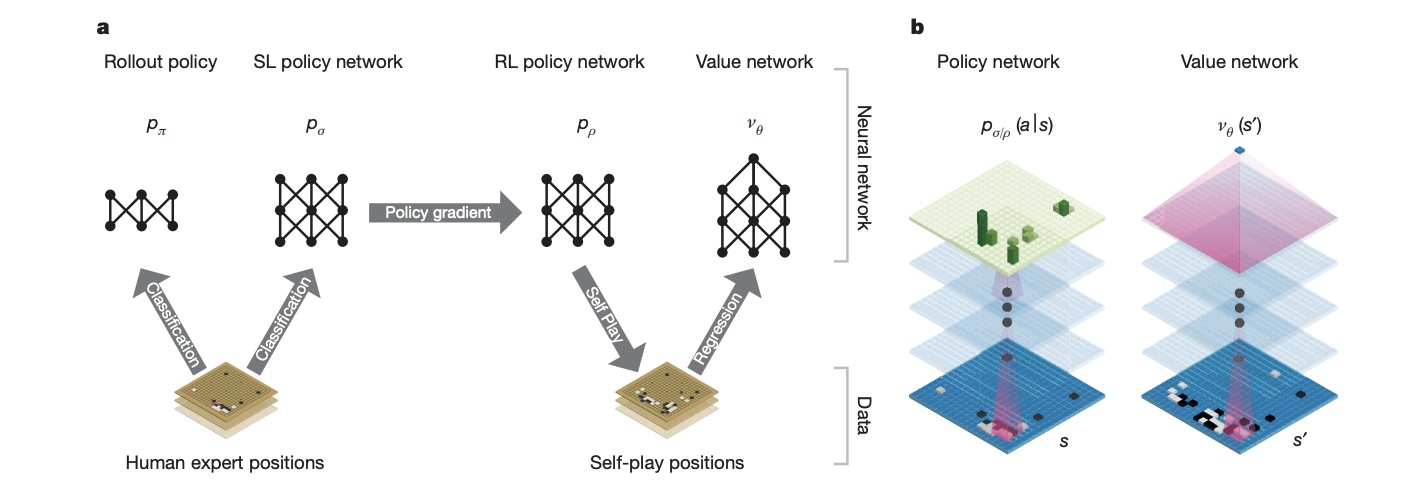
AlphaGo的每个大的版本迭代,都有相应的论文公布了其主要的成果和做法,下图是第一个版本的AlphaGo的架构:
而在最近这几年,谷歌在AI和深度学习领域内,最具有影响性的,应该是下面这两篇论文了:
- 2017年的《Attention Is All You Need》,这篇论文基于Encoder-Decoder架构,使用多头的自注意力机制,提出了新的名为Transformer的架构,Transformer架构是当下很多大模型构建的基础。

-
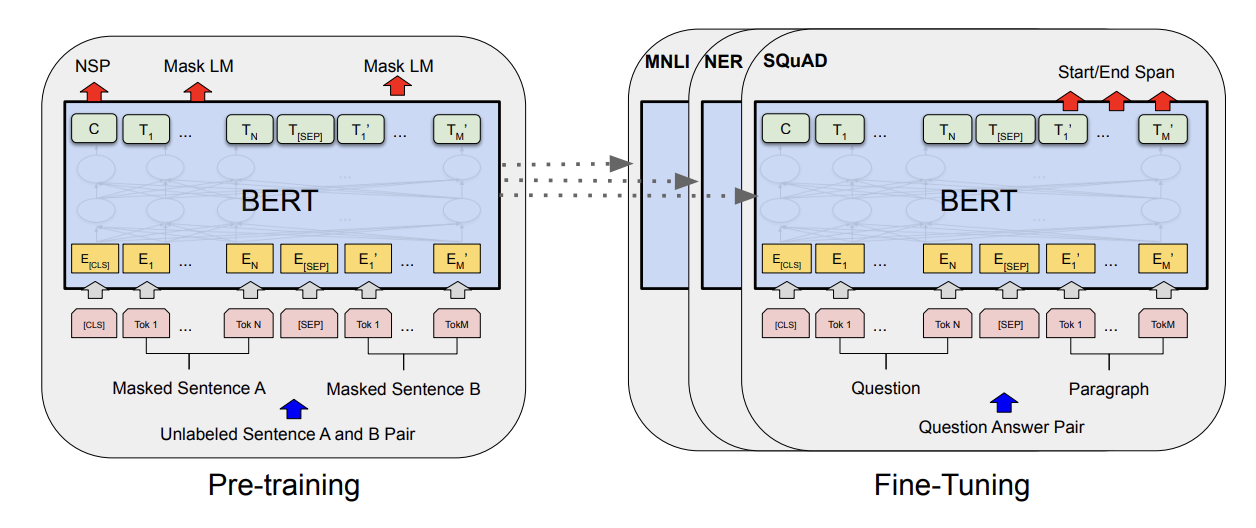
2018年11月,谷歌发布《Pre-training of Deep Bidirectional Transformers for Language Understanding》论文,提出了预训练模型BERT,通过预训练(Pre-training)+ 微调(Fine-Tuning),实现使用同一个基模型解决一类NLP问题的目标。
6.3 OpenAI
2015年11月,出于对抗大公司人工智能研究可能给人类带来的战争、道德伦理风险,阿隆·马斯克(Elon Musk)和萨姆·阿尔塔曼等(Sam Altman)人创建了非盈利的AI研究组织——OpenAI。
OpenAI最开始加入的10为研究员,其中有5位都是来自谷歌,其中包括AlexNet的二作伊利亚·萨特斯基弗。所以在当时,OpenAI被哈萨比斯公开攻击了很久(见面就掐,有机会就骂)。
OpenAI在最初几年,基于非盈利模式运营,实际遭遇了巨大的困难。2017年3月,GAN之父伊恩·古德费洛(Ian Goodfellow)离开OpenAI重回谷歌;2017年6月,马斯克挖走了安德烈·卡普西(Andrej Karpathy),任命其为特斯拉人工智能的主管(马斯克有时候做事情真的是……);2018年2月,马斯克也离开了OpenAI。
马斯克离开之后,阿尔特曼接手了OpenAI,并将OpenAI重组为一家盈利公司。OpenAI最终还是变成了一家公司,怀着造福全人类崇高理想的时间,总共加起来也没超过四年。
OpenAI最为出圈的工作,便是GPT系列了,这真的是十年寒窗无人问,一举成名天下知。而GPT的出圈,也充分诠释了什么叫做大力出奇迹。
- 2018年6月,OpenAI也发布了自己的预训练模型,参数量1.17亿。这篇论文的名字叫《Improving Language Understanding by Generative Pre-Training》。在这篇论文中OpenAI使用Transformer的解码器架构,首次提出了在NLP领域使用预训练模型的概念。但是,在同年11月,谷歌发布了BERT,使用Transformer的编码器架构进行预训练。结果在相同模型参数的情况下,全面胜出了GPT-1。
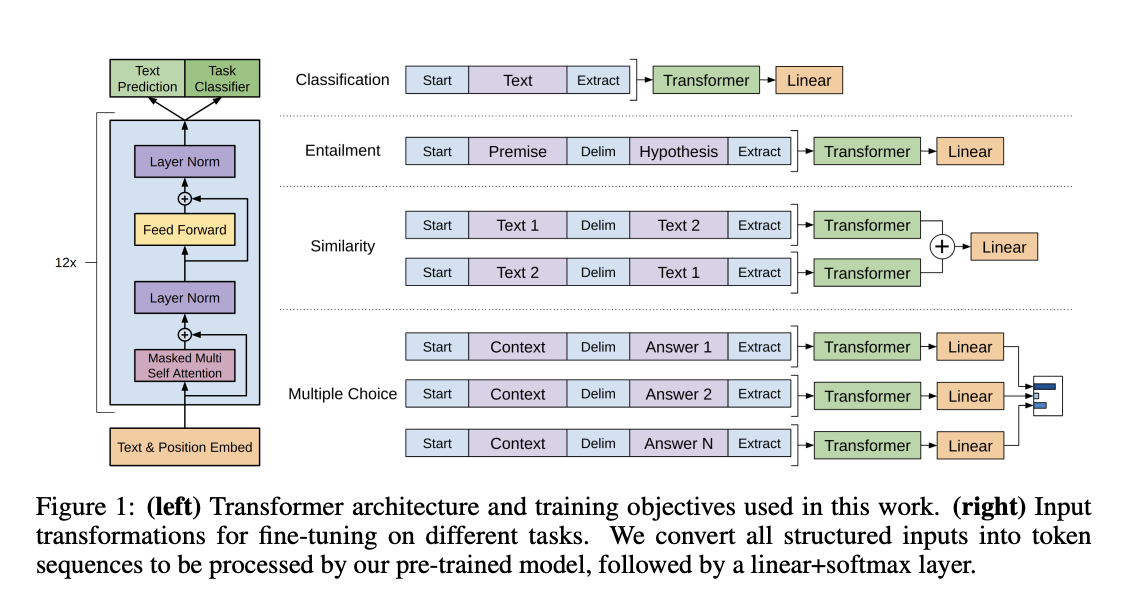
-
2019年,OpenAi发布了GPT-2的论文《Language models are unsupervised multitask learners》,模型参数15亿。虽然将模型参数调高了十倍不止,效果却比较一般。不过在这篇论文中,OpenAI提出可以将预训练模型应用于Zero Shot场景下作微调,并且提出了Prompt概念。另外从实验结果来看,同样的模型架构,在增加数据量,增加模型高度,调深模型宽度后,模型效果会有明显提升。
-
2020年5月,OpenAI发布了GPT-3的论文《Language Models are Few-Shot Learners》,模型参数1750亿,这次整整将模型参数量调高了100多倍。这次的模型效果非常好,在很多NLP任务上都取得了最好成绩。并且在这篇论文中,OpenAI提出了in-context learning(就是调试prompt,让模型能得到更好的结果),最大的不同是in-context learning给的样本数据不会触发模型的梯度更新,仅对本次交互有效。
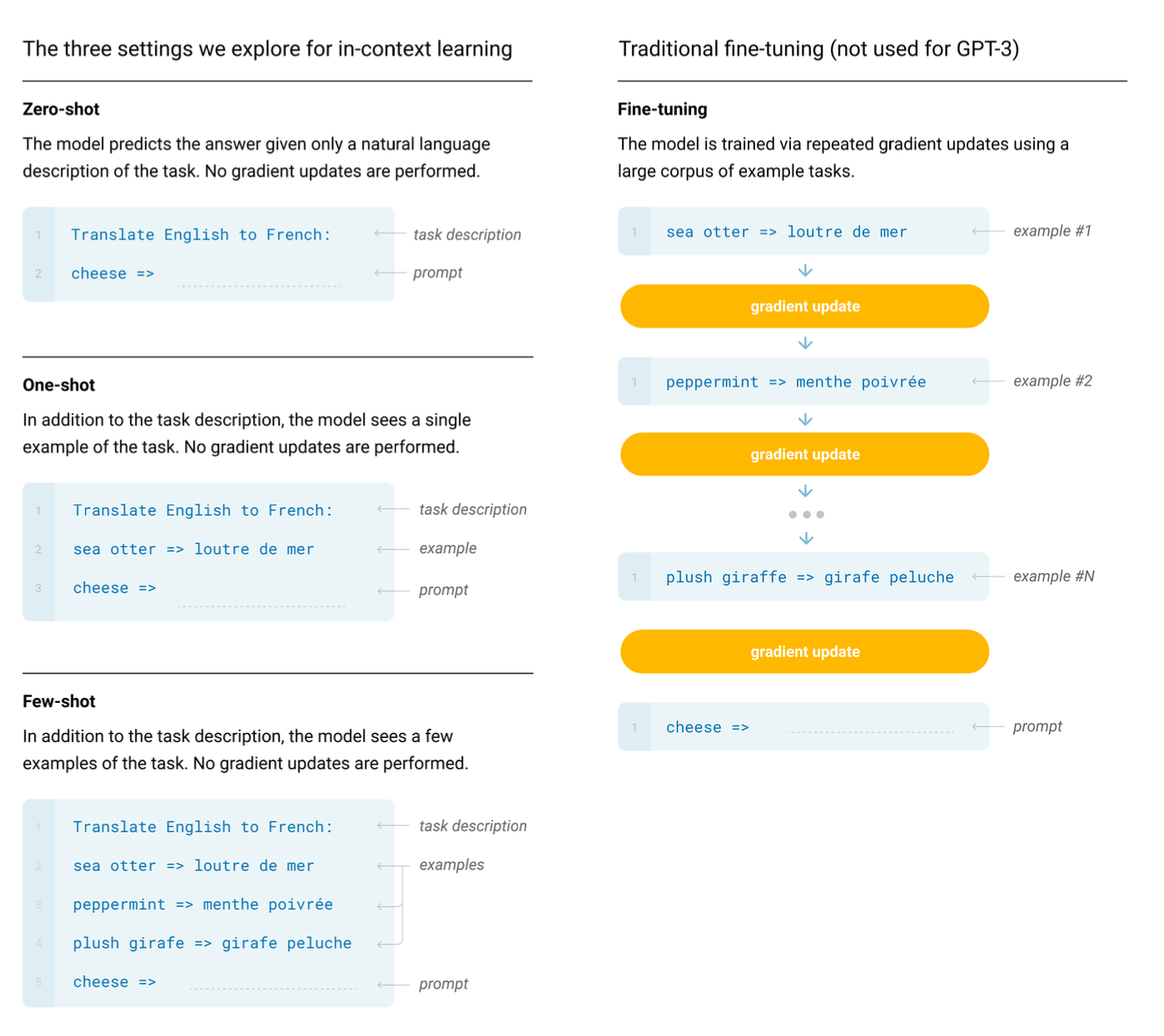
-
2022年3月,OpenAI发布了名为"text-davinci-003"的全新版本GPT-3(这便是被大众所熟知的GPT-3.5,模型参数量不变)。这次模型的效果很好,以GPT-3.5作为底层模型的ChatGPT应用,在推出仅两个月时间,月活用户便突破1亿,成为史上用户增长最快的消费者应用。OpenAI这次是真的出圈了,而GPT-3的论文在发布的三年多时间,也已经被引用了超万次。
7. 结语
神经网络的发展经历了六十多年,期间起起伏伏,几经衰败和繁荣,一路走来发生了很多有趣的故事。技术、科学、伦理、利益等各种因素相互交错,互相影响,在历史的车轮下滚滚向前。
在当下,神经网络已被大模型所垄断,模型参数动辄上千亿,已经不再是普通玩家可以玩得起的级别了。大语言模型除了解决NLP相关领域问题之外,似乎也展示了可以解决其他领域问题的能力,看起来我们确实离AGI已经很近。
然而,我们离AGI的距离是近是远,依旧没有人能说清楚。很多技术往往是多年没有大的进步,在某个时刻就突然具备了天时、地利、人和等多方面因素,以一种意料不到的形式产生了突破。也有很多时候,当大家都觉得未来已来,却突然间一切归零,原地踏步。
而当AGI真正到来的那一刻,人类社会究竟会发生什么样的变化,是会带来如阿隆·马斯克所说的彻底毁灭,还是如拉里·佩奇所说的再次进化?人类社会是否准备好了接受这样的变革和冲击?技术的发展,除了给我们带来认知层面的革命之外,还有越来越多的未解之谜……
参考文献
History of AI Winters - Actuaries Digital - History of AI Winters | Actuaries Digital
https://en.wikipedia.org/wiki/Artificial_general_intelligence
https://en.wikipedia.org/wiki/ENIAC
https://www.cnblogs.com/yymn/p/15216422.html
McCulloch W S, Pitts W. A logical calculus of the ideas immanent in nervous activity[J]. The bulletin of mathematical biophysics, 1943, 5: 115-133.
https://en.wikipedia.org/wiki/Warren_Sturgis_McCulloch
https://en.wikipedia.org/wiki/Walter_Pitts
https://en.wikipedia.org/wiki/Donald_O._Hebb
https://en.wikipedia.org/wiki/Turing_test
Rosenblatt F. The perceptron: a probabilistic model for information storage and organization in the brain[J]. Psychological review, 1958, 65(6): 386.
https://en.wikipedia.org/wiki/Perceptron
https://en.wikipedia.org/wiki/IBM_704
Minsky M, Papert S. An introduction to computational geometry[J]. Cambridge tiass., HIT, 1969, 479(480): 104.MLA
《深度学习革命》
https://en.wikipedia.org/wiki/Perceptrons_(book)
http://www.cs.toronto.edu/~hinton/absps/naturebp.pdf
从反向传播推导到梯度消失and爆炸的原因及解决方案(从DNN到RNN,内附详细反向传播公式推导) - 知乎
Pomerleau D A. Alvinn: An autonomous land vehicle in a neural network[J]. Advances in neural information processing systems, 1988, 1.
https://en.wikipedia.org/wiki/Convolutional_neural_network
https://web.archive.org/web/20171228091645/http://deeplearning.net/tutorial/lenet.html
Le Q V. Building high-level features using large scale unsupervised learning[C]//2013 IEEE international conference on acoustics, speech and signal processing. IEEE, 2013: 8595-8598.
LeCun Y, Bottou L, Bengio Y, et al. Gradient-based learning applied to document recognition[J]. Proceedings of the IEEE, 1998, 86(11): 2278-2324.MLA
AlphaGo之父戴密斯·哈萨比斯:是天才,也是生活里的普通人-腾讯云开发者社区-腾讯云
Silver D, Huang A, Maddison C J, et al. Mastering the game of Go with deep neural networks and tree search[J]. nature, 2016, 529(7587): 484-489.
Vaswani A, Shazeer N, Parmar N, et al. Attention is all you need[J]. Advances in neural information processing systems, 2017, 30.
Radford A, Narasimhan K, Salimans T, et al. Improving language understanding by generative pre-training[J]. 2018.


