数据结构：七大内部排序图文详解_c语言数据结构内部排序法

排序

定义：设有记录序列：{ R1、R2 ………… Rn }
其相应的关键字序列为： { K1、K2 ………… Kn };
若存在一种确定的关系： Kx <= Ky <= … <= Kz则将记录序列 { R1、R2 ………… Rn }
排成按该关键字有序的序列 { Rx、Ry ………… Rz } 的操作，称之为排序。

内部排序

定义：全部记录都可以同时调入内存进行的排序

注意：关系是任意的，如通常使用的小于、大于关系。

直接插入排序

就如名字一样，找到当前项在当前有序序列的插入位置，然后插入，这样就需要向后移动该位置后边的项，这样序列中当前项就会被前一项的值覆盖。此时 r[0] 用作哨兵（哨兵的作用是保存当前项的值，也可以用一个变量来做为哨兵）。

例：36、24、10、6、12存放在 r 数组的下标为 1 至 5 的元素之中，用直接插入法将其排序。结果仍保存在下标为 1 至 5 的元素之中。

当前项为 24 时，哨兵值为 24，当前有序序列就只有 36 一项，并且 24 < 36，所以 24 应该插在 36 的位置，36 向后移一位，那么当前排序完成，下标为 1 的项值应为哨兵的值。

每遍操作：

1. 先用哨兵记录当前项。
2. 再将当前项同已排序的序列，从尾开始进行比较。在已排序的序列中寻找自己的位置，进行插入
3. 或者寻找不到，则一直进行到哨兵为止。意味着本元素最小，应该放在 num[1] 。

每一遍，排序的序列将增加一个元素。如果序列中有 n 个元素，那么最多进行n 遍即可。

void insert_sort(int num[],int len) {
	for (int i = 2; i < len; i++) {		//遍历数组排序
		num[0] = num[i];
		int j = i - 1;
		while (j <= 0) {					//在前i个有序数组找插入位置
			if (num[0] < num[j]) {		//第i个元素小于第j个元素，将第j个元素向后移
				num[j + 1] = num[j];
			}else if (j == 0) {			//若j==0，则第i个元素在前i个元素中最小
				num[1] = num[0];
			}else {
				num[j + 1] = num[0];//第i个元素大于第j个元素，则第j+1个元素等于第i个元素
				break;
			}
			j--;
		}
	}
	for (int i = 1; i < len; i++) {
		printf("%d ", num[i]);
	}
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20

时间复杂度为：T(n)=O(n²)
辅助空间：S(n)=O(1)

折半插入排序

与直接插入排序的不同之处就是使用用折半查找方法确定插入位置。

void bininsert_sort(int num[], int len) {
	for (int i = 2; i < len; i++) {
		num[0] = num[i];					//更新标志
		int low = 1, hight = i - 1,mid;		//初始化头尾指针		
		while (low <= hight) {				//折半寻找合适位置
			mid = (hight + low) / 2;
			if (num[0] < num[mid]) {
				hight = mid - 1;
			} else {	
				low = mid + 1;
			}
		}
		for (int j = i - 1; j >= low; j--) {//循环后移元素，为插入准备
			num[j + 1] = num[j];
		}
		num[low] = num[0];					//插入
	}
	for (int i = 1; i < len; i++) {
		printf("%d ", num[i]);
	}
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21

时间复杂度：T(n)=O(n²)
辅助空间：S(n)=O(1)

希尔排序

过程：

1. 先取一个正整数 gap<n，把所有相隔 gap 的记录放一组，组内进行直接插入排序；
2. 然后减小 gap 值，重复上述分组和排序操作；
3. 直至 gap=1，即所有记录放进一个组中排序为止。

希尔排序实际是步长递减的多次直接插入排序过程。

特点:
子序列的构成不是简单的“逐段分割”，而是将相隔某个增量的记录组成一个子序列。希尔排序可提高排序速度，因为分组后n值减小，T(n)=O(nlogn)，关键字较小的记录跳跃式前移，在进行最后一趟增量为1的插入排序时，序列已基本有序。辅助空间：S(n)=O(1)

void shell_sort(int num[], int len) {
	int i, j;
	for (i = len/2; i >= 1; i /=2) {			//循环n趟
		for (j = 1 + i; j < len; j++) {			//循环i次（进入直接插入排序）
			num[0] = num[j];
			int k = j - i;
			while (k > 0 && num[0] < num[k]) {	//每个小组内比较移动
				num[k + i] = num[k];
				k -= i;
			}
			num[k + i] = num[0];				//插入位置要比k大i
		}
	}
	for (int i = 1; i < len; i++) {
		printf("%d ", num[i]);
	}
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17

增量序列取法:
最后一个增量值必须为1；

冒泡排序

将第一个记录的关键字与第二个记录的关键字进行比较，若为逆序r[1].key>r[2].key，则交换；然后比较第二个记录与第三个记录；依次类推，直至第n-1个记录和第n个记录比较为止——第一趟冒泡排序，结果关键字最大的记录被安置在最后一个记录上

对前n-1个记录进行第二趟冒泡排序，结果使关键字次大的记录被安置在第n-1个记录位置
重复上述过程，直到“在一趟排序过程中没有进行过交换记录的操作”为止

void bubble_sort(int num[], int len)
{
	bool flag = 1;							//交换标志
	int i = len;
	while (i>2&&flag) {
		flag = 0;
		for (int j = 1; j + 1< i; j++) {
			if (num[j] > num[j + 1]) {		
				int tem = num[j];
				num[j] = num[j + 1];
				num[j + 1] = tem;
				flag = 1;
			}
		}
		i--;
	}
	for (int i = 1; i < len; i++) {
		printf("%d ", num[i]);
	}
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20

时间复杂度T(n)=O(n²)
辅助空间：S(n)=O(1)

选择排序

排序过程：

1. 首先通过n-1次关键字比较，从n个记录中找出关键字最小的记录，将它与第一个记录交换；
2. 再通过n-2次比较，从剩余的n-1个记录中找出关键字次小的记录，将它与第二个记录交换；
3. 重复上述操作，共进行n-1趟排序后，排序结束

void smp_sort(int num[], int len)
{
	for (int i = 1; i < len ; i++) {
		int min = i;
		for (int j = i + 1; j < len; j++) {
			if (num[j] < num[min]) {
				min = j;
			}
		}
		if (i != min) {
			int tem = num[i];
			num[i] = num[min];
			num[min] = tem;
		}
	}
	for (int i = 1; i < len; i++) {
		printf("%d ", num[i]);
	}
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19

时间复杂度：T(n)=O(n²)
辅助空间：S(n)=O(1)

选择排序和冒泡排序对比：其实这两种排序方法很相似，只不过选择排序是指定第 i 项与后边 n-i 项对比，第 i 项永远存着最大或最小项。而冒泡排序则是第 i 项与第 i + 1 项对比，第 i+1 项永远存着最大或最小项。

快速排序

通过一趟排序，将待排序记录分割成独立的两部分，其中一部分记录的关键字均比另一部分记录的关键字小，则可分别对这两部分记录进行排序，以达到整个序列有序

排序过程：

1. 对num[s……t]中记录进行一趟快速排序，附设两个指针 i 和 j，初始时令 i=s，j=t，x (标准)
2. 首先从 j 所指位置向前搜索第一个关键字小于 x 的记录，并和 i 位置项交换
3. 再从 i 所指位置起向后搜索，找到第一个关键字大于 x 的记录，和 j 位置项交换
4. 重复上述两步，直至i==j为止
5. 再分别对两个子序列进行快速排序，直到每个子序列只含有一个记录为止

如下图第一个标准（privot）选中的就是 49。

void k_sort(int num[], int low, int hight)
{
	int  i = low, j = hight, x = num[i];
	if (low >= hight)
		return;
	while (i < j) {						//i>j说明排序完成
		while (i < j&&num[j] >= x)		//i指向标志元素,移动j找位置
			j--;						
		if (i < j) {
			num[i] = num[j];			//使i指向的元素等于j指向的元素指向的元素
			i++;
		}
		//接下来移动i指针
		while (i < j&&num[i] <= x)
			i++;
		if (i < j) {
			num[j] = num[i];
			j--;
		}
	}
	num[i] = x;					//找到放置标志元素位置，最后
	k_sort(num, low, j - 1);	//递归排序x位置左边的元素
	k_sort(num, j + 1, hight);//递归排序x位置右边的元素
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24

最好情况（每次总是选到中间值作枢轴） T(n)=O(nlog2n)
最坏情况（每次总是选到最小或最大元素作枢轴）T(n)=O(n²)
辅助空间：需栈空间以实现递归
最坏情况：S(n)=O(n)
一般情况：S(n)=O(log2n)

由上述最好情况可以得出选取标准 x(pivot) 对于快速排序至关重要，将直接影响其性能，我这里是每次就选当前序列的第一项为基准，其实这样并不好，有一种方法可以使用随机数来增大 pivot 刚好是序列的中间值的概率。

堆排序

排序过程：
将无序序列建成一个堆，得到关键字最小（或最大）的记录；输出堆顶的最小（大）值后，使剩余的n-1个元素重又建成一个堆，则可得到n个元素的次小值；重复执行，得到一个有序序列

大顶堆：满足Key[i]>=Key[2i+1]&&key>=key[2i+2]称为大顶堆，简单来说就是双亲节点的值总是大于孩子结点，而兄弟节点之间没有约束，左孩子可以大于右孩子，也可以小于右孩子。
小顶堆：满足 Key[i]<=key[2i+1]&&Key[i]<=key[2i+2]称为小顶堆，双亲节点的值总是小于孩子结点。
特点： 可将堆序列看成完全二叉树，则堆顶元素（完全二叉树的根）必为序列中n个元素的最小值或最大值。

堆排序要解决的问题：

• 如何在输出堆顶元素之后，调整剩余元素，使之成为一个新的堆？

第二个问题解决方法——筛选

输出堆顶元素之后，以堆中最后一个元素替代之；然后将根结点值与左、右子树的根结点值进行比较，并与其中小者进行交换；重复上述操作，直至叶子结点，将得到新的堆，称这个从堆顶至叶子的调整过程为“筛选”。

例：
小顶堆排序

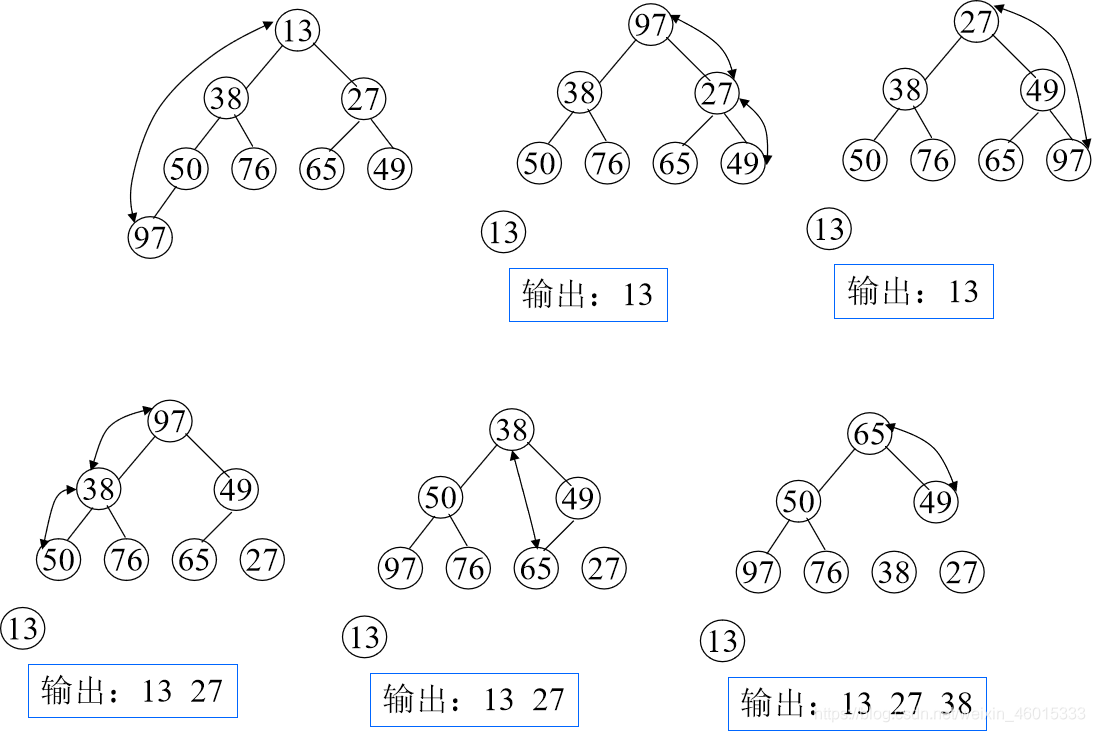
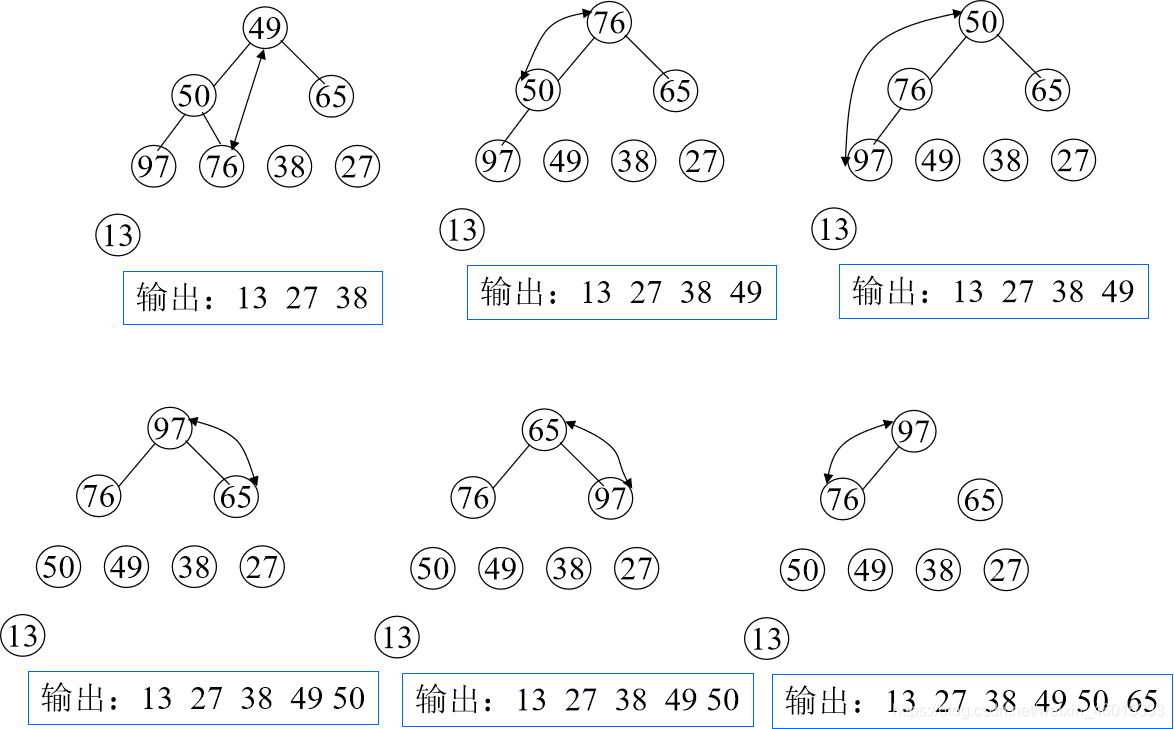
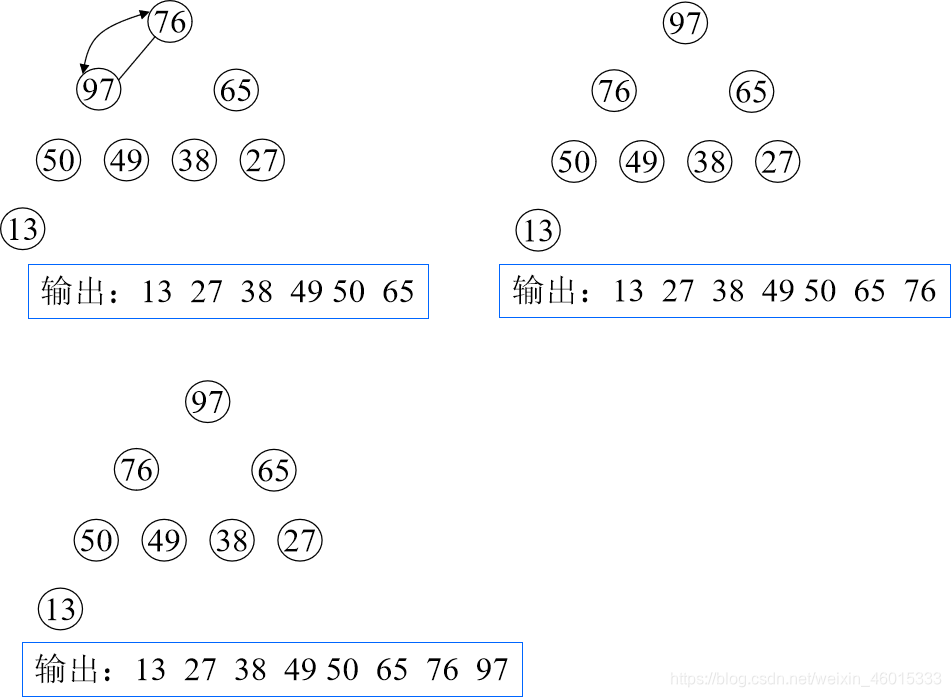
void buildd_1(int num[], int len)						//从根节点向下建小顶堆
{
	for (int i = 1; i < len; i++) {
		int j = i;
		while (j != 0 && num[j] < num[(j - 1) / 2]) {//孩子节点逐一与双亲节点比较
			int tem = num[j];
			num[j] = num[(j - 1) / 2];
			num[(j - 1) / 2] = tem;
			j = (j - 1) / 2;
		}
	}
}
void buildd_2(int num[],int i, int len) //自底向上建小顶堆
{
	int child = 2 * i + 1;
	int parent = i;
	while (child < len) {//小的孩子节点与双亲节点比较
		if (child + 1 < len && num[child] > num[child + 1]) {//找值小的孩子结点下标
			child++;
		}
		if (num[parent] > num[child]) {//改变了前边部分有序的值，就需要从新与变动过的地方比较
			int tem = num[parent];
			num[parent] = num[child];
			num[child] = tem;
			parent = child;//值变动，改变双亲的下标值，再比较
		}
		else//没有变动则说明当前序列符合小顶堆规则，退出循环比较
			break;
		child = child * 2 + 1;//更新孩子结点下标
	}
}
void buildd_3(int num[], int len)			//自上而下建大顶堆
{
	for (int i = 1; i < len; i++) {
		int j = i;
		while (j != 0 && num[j] > num[(j - 1) / 2]) {
			int tem = num[j];
			num[j] = num[(j - 1) / 2];
			num[(j - 1) / 2] = tem;
			j = (j - 1) / 2;
		}
	}
}*/

void buildd_4(int num[], int i, int len)				//自下而上建大顶堆
{
	int child = 2 * i + 1;
	int parent = i;
	while (child < len) {
		if (child + 1 < len && num[child] < num[child + 1]) {
			child++;
		}
		if (num[parent] < num[child]) {
			int tem = num[parent];
			num[parent] = num[child];
			num[child] = tem;
			parent = child;
		}
		else
			break;
		child = child * 2 + 1;
	}
}
void buildHeap(int array[], int size) {
	for (int i = size / 2 - 1; i >= 0; i--) { //倒数第二排开始,创建大顶堆，必须从下往上比较
		buildd__2(array, i, size); 
		//buildd__4(array, i, size);                // 否则有的不符合大顶堆定义
	}
}

int main()
{
	int num[10] = { 0,12,4,54,3,5,78,34,22,90 };
	
	buildHeap(num, 10);
	//自上而下堆排序
	for (int i = 9; i >= 0; i--) {//建好堆后交换根结点和当前序列最后一个节点
		int tem = num[i];
		num[i] = num[0];
		num[0] = tem;
		buildd_2(num, 0, i);
		//buildd_4(num, 0, i);
	}
	/*	自上而下堆排序
		buildd_1(num, 0, i);
		for (int i = 9; i >= 0; i--) {
		int tem = num[i];		
		num[i] = num[0];
		num[0] = tem;
		buildd_1(num, 0, i);
		//buildd_3(num, 0, i);
	}*/
	for (int i = 0; i < 10; i++) {
		printf("%d ", num[i]);
	}
	return 0;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97

时间复杂度：T(n)=O(nlogn)；
辅助空间：S(n)=O(1)。

内部排序基本就这些内容了，朋友们下次见！！！我是孤城浪人，一名正在前端摸爬滚打的菜鸟，欢迎你的关注。