深度学习入门与实战（四）- 卷积神经网络_sigmoid单元逻辑门

上一讲我说到了线性回归模型，它可以帮助我们解决房价预测等回归、拟合的问题，我们也可以对回归方程 f(x)输出加一个 Sigmoid 函数，使其也能应用在分类问题上。

但现实中除了分类问题还有很多不同的场景，会用到图像算法、文本算法、音视频算法等等。今天，就让我来带你学习卷积神经网络（Convolutional Neural Networks，CNN）在图像，音频上的应用。

卷积神经网络在人脸识别、智慧医疗、工业检测等方面有着广泛的应用，极大地缩减了人力物力的投入，并有着比人类更高效精确的表现。

接下来，为帮助你更好地理解卷积神经网络，我们先来看几个与之相关的概念，它们分别是卷积、激活函数、池化和感受野。

卷积

卷积在卷积神经网络中的主要作用是提取图片的特征，同时保留原来图片中各个像素的相对位置（空间）关系。举个例子，假设我们有 1 个 5x5 的矩阵 A 和 1 个 3x3 的矩阵 B，我们将这两个矩阵进行卷积操作（这有点类似点乘计算），操作过程如下图：

在这个过程中总共出现了 3 种矩阵：

1. 原始图像的矩阵（A），这个实际上就是我们眼睛看到的世界。
2. 3x3 矩阵（B），我们称为滤波器（Filter）、核（Kernel），或是特征提取器、卷积核。通过对滤波器矩阵设置不同的值，可以实现如边缘检测、锐化以及模糊操作等不同的操作。在实际的模型设计中，我们会使用不同尺寸的滤波器来实现不同的效果。通常我们只需要设定滤波器的尺寸和数量，卷积神经网络就可以自己通过梯度更新或反向传播得到内部的数值。使用越多的滤波器，可以提取到越多的图像特征，神经网络也有更好的性能。
3. 卷积之后得到的矩阵（C），我们称为特征图（Feature Map、 Activation Map）。

如下图 4，原始图片是一张小动物，通过不断变化卷积核的内容，就可以得到不同的结果，有的是轮廓信息（第 2、3、4 行），有的是更加锐化后的信息（第 5 行），有的会变得模糊（第 6、7 行）。

讲解了卷积之后，我需要补充两个知识点：边缘填充和特征图尺寸的计算。

图 3 的计算当中，我们实际上是将滤波器和图像进行了对齐：第一步，滤波器（黄色虚线框）的第 1 个像素和图像的第 1 个像素是重叠的；最后一步，滤波器（棕色虚线框）的最后 1 个像素和图像的最后 1 个像素也是重叠的，这意味着滤波器没有超出图像。

如果我们在输入图像的周围填充一些 0，再把滤波器应用到这些边缘的点上，让滤波器“超出来”一些，这就叫作边缘填充。如下图，蓝色的矩阵是原始图像，外面一圈黄色的 0 就是边缘填充的值，虚线框内是卷积核。通过边缘填充，我们可以控制输出的特征图的大小。

既然说到了特征图的大小，那特征图的大小又跟哪些方面有关呢？这就是我接下来要补充的。

特征图尺寸的计算。假定：O=输出图像的尺寸，I=输入图像的尺寸，K=卷积层的核尺寸，S=移动步长，P=填充数。那么，输出图像尺寸的计算公式即为：O=(I-K+2P)/S+1。

以图 5 为例，I=4，K=3，P=1，S=1（假设我们每次移动 1 格），则输出尺寸 O=(4-3+2x1)/1+1=4。

这个公式非常重要。在设计神经网络结构的时候，神经网络的每一层都是由上一层得到的，只有确保每个层的尺寸无误才能保证神经网络的正常运转。

至此，你对卷积神经网络最基本的运算过程就有了一个大致的了解。接下来，我会介绍卷积神经网络中的另一个概念，激活函数。

激活函数

假设我们有一个简单的神经网络，如图：

这是一个 2 层的网络，其中 X1、X2 是输入，b1、b2 和 b3 是中间层的神经元，第一层是 b1 和 b2，第二层是 b3，Y 是输出。连接线的多个 w 值，对应神经元的权重。其中：

b1 的输出 = w11X1 + w21X2 + b1

b2 的输出 = w12X1 + w22X2 + b2

b3 的输出 Y = w13b1 + w23b2 + b3

=w13*(w11X1 + w21X2 + b1) + w23(w12X1 + w22*X2 + b2) + b3

=(w11w13 + w12w23)X1 + (w21w13 + w22w23)X2 + (b1w13 + b2w23 + b3)

这意味着，X1、X2 前面的系数仍然是一个常数，那么整个网络的输出就可以用 Y=X1Wa + X2Wb + B 来表示，折腾了一顿最后还是一个线性函数。这就相当于做了无用功，一层就能做到的事情，我用了好多层来做。

如果你有一个很大的网络，但是网络内部全都是线性单元，那这个网络一定可以被某种线性组合表示，你的隐藏层（如图 6 中的 b1、b2）就一点作用没有。所以，我们需要在网络中增加非线性函数，即激活函数（也称激励函数），以便让模型有更好的学习能力，或者说更好的特征提取和组合能力，毕竟这个世界有很多问题如天气预测、人脸识别，都是线性模型无法搞定的。

激活函数的种类非常多，常见的一般有：Sigmoid、tanh、ReLU 和Leaky ReLU。
先来看Sigmoid 函数。

在信息科学中，由于其单增以及反函数单增等性质，Sigmoid 函数常被用作神经网络的激活函数。它可以把输入的数值约束到 0~1 的范围内，无论是多大或者是多小的数，都可以使其无限逼近于 0 或 1。如下图：

不过，现在 Sigmoid 的使用率在逐渐减少，还记得之前课程中咱们提到过的梯度消失和爆炸问题吗？Sigmoid 的导数是一个驼峰状的函数，取值范围在 0~0.25 之间，当网络层数比较多的时候，多个接近于 0 的数相乘，最后的值就趋近于 0，所以它比较容易引发梯度消失问题，最终导致模型无法正常学习。此外，Sigmoid 函数含有幂运算，在大型网络中幂运算是非常消耗时间的。

我们再来看tanh 函数。

tanh 是双曲函数中的一个，为双曲正切。在数学中，双曲正切“tanh”是由双曲正弦和双曲余弦这两种基本双曲函数推导而来的。tanh 函数也是一个较为常用的激活函数，其公式与图像如下所示：

可以看到，跟 Sigmoid 一样，tanh 函数求导之后的值域仍然在 0～1 之间，所以它也没有解决梯度和幂运算计算量大的问题。

接下来是ReLU 函数。

ReLU 函数又称修正线性单元，是一种人工神经网络中常用的激活函数。ReLU 的公式非常简单：Relu=max(0,x)。从图可以看到，当 x≤0 的时候，函数等于 0，而 x＞0 的时候，函数的值就是 x。

ReLU 函数看似很简单，但简单并不意味着不好用。

当输入＜0 时，ReLU 函数的输出始终等于 0，因此函数的变化率为 0；当输入≥0 时，输出就是输入，因此，它的导数等于 1。

从对 ReLU 函数的描述可以看到，ReLU 函数不仅很大程度上解决了梯度消失的问题，还有着非常快的计算速度，因为它只需要判断是否大于 0 就行了。

当然，它也不是完美的，“ReLU 死区”就是一个很常见的问题，即：在训练一段时间以后，如果某个神经元在某次权重更新之后为负数，那它的激活函数就只会输出 0，这意味着这个神经元“死”掉了，以后再也不会输出其他的值了。例如，在一些特殊的情况下，比如学习率太大，就很容易导致更新后权值为负，从而引发神经元的“死亡”。

最后是Leaky ReLU 函数。

为了解决 ReLU 的致命缺点，脱胎于 ReLU 的 Leaky ReLU 函数应运而生，它的公式是f(x)=max(αx,x)。如下图：

α 是一个超参数，定义了 x<0 时的斜率，比如 0.01。这个小的斜率可以保证激活函数不会出现神经元“死亡”的情况。

池化

卷积操作之后，图片被转化成一张张特征图，数据量有时会很大，所以我们需要一种方式来尽可能地减少计算。于是便有了池化（Pooling）。池化实际上是一种降采样的形式，在尽量保留特征的同时，不断减少数据大小，从而减少参数量和计算量，比如我们压缩 1 张照片，照片大小被压缩后，其中的信息通常不会损失太多。

较为常见的池化有两种：最大池化（Max Pooling）和平均池化（Average Pooling）。

最大池化，顾名思义，就是在一张图内，选择一个池化尺寸，然后选择该尺寸中数值最大的像素点，添进新的特征图，直到该行为覆盖了整张图片。最大池化保留了数据内响应最大也是最强烈的值，相当于保留了照片中最重要的像素点，因此可以在减少计算的同时保留特征。

例如下图，选择池化尺寸为 2x2，在其中分别选出最大值，通过对 4 块区域的最大池化，最终构成了右边新的特征图。

平均池化，也叫均值池化，它是把特征图一个区域内的全部数值取平均值的池化方法。在操作上与最大池化相似，只不过最大池化是取最大值，而平均池化是取区域内数值和的平均数。

池化之后，新生成的特征图的尺寸会发生变化，假设 I=输入图像的尺寸，F=卷积层的核尺寸，S=移动步长，则输出尺寸 O=(I-F)/S+1。

以上图为例：I=4，F=2，虚线框处理完蓝色的部分后，会往右挪动 2 格，处理黄色的部分，因此 S=2，则 O=(4-2)/2 + 1=2。

在实际使用过程中，两种池化有不同的侧重点。最大池化因为提取的是区域内的特征最强烈的像素，所以一般在网络的前几层使用，用来保留图像的纹理信息，但走到深层的网络之后，特征图的尺寸越来越小，包含的语义信息逐渐增多，最大池化能够获取的信息就会减少。此时，平均池化的优势就显现出来了，在深层的网络中，它依然能够很好地保留背景和语义信息。

感受野

在卷积神经网络中，感受野（Receptive Field）是指卷积神经网络每一层输出的特征图上的像素点在输入图片上映射的区域大小，也就是特征图上的一个点对应输入图上的区域。感受野跟步长、卷积核尺寸有关，计算公式如下：

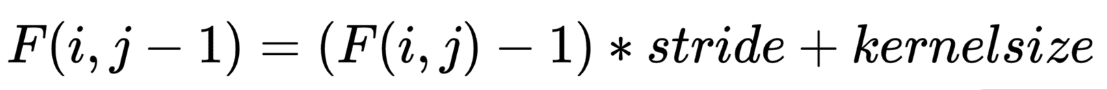
其中F(i, j)表示第 i 层对第 j 层的局部感受野， stride为卷积核移动步长，kernelsize为卷积核尺寸。

通过公式，你可以将感受野简单地理解为像素能够感应的范围大小。在后续的学习中，我们还会多次遇到它，希望你能够记住它的定义。

卷积神经网络

我们回忆一下之前提起的神经网络模型。当网络输入一个数据之后，中间要经过若干个隐藏层，如果每一个隐藏层中的每一个神经元都跟前一层的神经元相连，会产生巨大的计算量。

举个例子，在一个如图 13 的全连接网络中，m-1 层有 1000 个神经元，m 层有 1000 个神经元，那么两层之间的全连接（图中蓝色的线）的数量就是 1000x1000=100 万个，如果神经网络有更多层，那连接的数量会变得更加庞大。

那有什么办法可以让连接的数量不那么多呢？

我们可以把 m 层中的每个节点都限定一下连接数量，比如每个节点只跟 10 个 m-1 层的神经元连接，如下图（图中只画出 3 个），这样一来，连接的数量就从 1 百万个变成了 10x1000=1 万个，减少了 100 倍。这个操作，就叫作稀疏连接（Sparse Connectivity），也叫参数减少。

现在 m 层的每个神经元连接的区域是 10 个神经元，如果我们把 m 层修改一下，改为只有相同的 10 个神经元的集合 F，然后用集合 F 不断地与 m-1 层的 10 个神经元连接，如下图所示：

集合 F 对应的操作，叫作权值共享，F 就是权值。换句话说就是每一次的连接都是用相同的权值，共享使用。你看，通过权值共享，连接的数量是不是又进一步减少了？

参数减少、权值共享是卷积神经网络最大的两个特点。

这时候你可能会有疑问，这个跟前面说的卷积计算方法为什么不太一样？

我们把 m-1 层的“一长条”神经元，变为方形或者矩形的像素矩阵，再把集合 F 也变成类似的方形矩阵，m-1 层就成了图片，集合 F 就成了卷积核（图 3），这就变成了卷积操作构成的网络，即卷积神经网络。

了解完卷积神经网络的概念和特点，我们就可以开始组装一个卷积神经网络了。在组装的过程中，你也能够更直观地了解卷积神经网络的构造和样式。

我们现在回顾一下，手头有什么可以用的零件：

1. 卷积核：提取特征。
2. 池化：减少参数和计算量。
3. 全连接层：分类。
4. 激活函数：表示更加复杂的学习过程。

活用它们，我们就能用卷积神经网络来做一个简单的分类网络了。

恰好我们手上有一张图片，我们先用若干个卷积核提取图片的特征（如刚才所说，不同的卷积核可以提取到图片不同的特征信息）。

经过卷积操作后，我们在特征图上加一个激活函数。如下图所示，我们提取了第一层的特征。

经过这一系列操作后，我们就有了很多提取出来的特征图。下一步，我们要对这些特征图变形，让它们变成向量的形式，这可以方便我们增加一层全连接层，从而将分类的结果映射到不同的类别上。如下图所示：

循环神经网络（RNN（Recurrent Neural Network））

下图是一个抽象的 RNN 基本单元结构。自底向上的三个蓝色的节点很显然，分别是输入层、隐藏层和输出层。U 和 V 分别是连接两个层的权重矩阵。如果不考虑右边的棕色环路的话，就是一个典型的全连接的网络。

那么这个环路是干吗的呢？我们不妨先将其展开：

现在看上去是不是明晰多了？ 在 t 时刻，网络接受输入 Xt 和来自 t-1 时刻的隐藏层状态 St-1，并产生一个 t 时刻的隐藏层状态 St，以及 t 时刻的输出 Ot。其公式化的表示为：

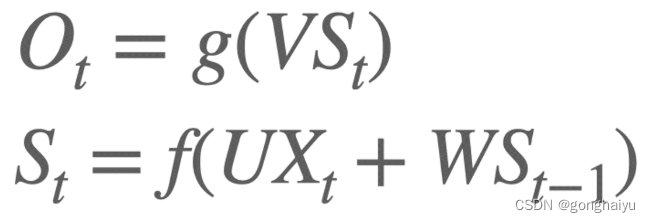
其中 g 和 f 是各自节点的激活函数。这里面需要注意的一点是，对于每一个时间 t，U、V、W 都是同一个，这非常类似上一节课讲到的权值共享。RNN 的权值共享主要出于两方面的考虑：

1、 减少参数量，也减少计算量。
2、 RNN 接受的输入是可变长的，如果不进行权值共享，那每个 W 都不同，我们无法提前预知需要多少个 W，实现上的计算就会非常困难。

以上我说说到的是典型的 RNN 的结构，实际上 RNN 有很多种变体。比如双向RNN（BiRNN）

相比于 RNN，BiRNN 维持了两个方向的状态。正向计算和反向计算不共享权重，也就是说 U、V、W 分别有两个，以对应不同的方向。其公式化的表示就变成了如下的形式：

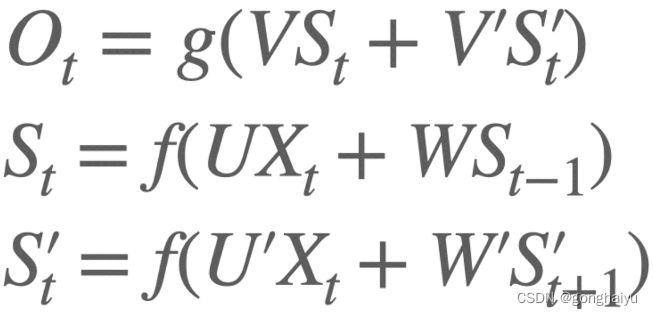
需要注意：S’在 t 时间接受的隐藏层状态不是来自 t-1，而是来自 t+1。

RNN 的梯度消失与爆炸

相对于全连接的方式，RNN 能够更好地处理序列相关的问题，但正是因为 RNN 需要考虑的内容是变长的，所以就会带来梯度相关的问题。我们根据之前的知识，明确以下函数关系。

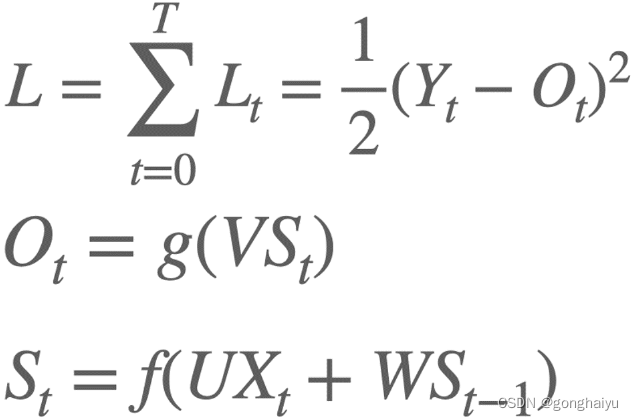
求梯度实际上是求 W、V、U 的偏导数。我们以 L 对 W 在 t 时刻求偏导数为例，推导过程如下：

可以发现，L 关于 W 的偏导数会随着序列的长度而产生长期依赖。

长期依赖是指当前系统的状态，可能受很长时间之前系统状态的影响，是RNN中无法解决的一个问题。

此外，别忘了还有激活函数 f 的存在。RNN 一般会使用 tanh 函数作为它的激活函数，而 tanh 的导数在 0~1 之间。如此一来，如果 W 也是在 0~1 之间，随着 t 的增大，梯度计算中连续相乘就会变得很长，很多个在 0~1 之间的数相乘会逐渐接近 0。梯度接近 0 则意味着梯度消失了；反之如果 W 很大，则梯度也会变得非常大，进而产生梯度爆炸，这是一个很严重的问题。

那我们怎么解决这个问题呢？

从上面的表述来看，问题出现在连续相乘的环节。那我们是不是可以把这个环节优化一下，不要让梯度消失或者爆炸就好了？这就是长短期记忆网络要做的事情。

长短期记忆网络

我们接下来看长短期记忆网络（Long Short-Term Memory，以下简称 LSTM）。

刚才提到 RNN 的梯度问题，其本质原因就是模型“记忆”的序列太长了，不管真实序列有多长都会一股脑地记忆和学习，从合理性的角度来看这并不是一个很好的方案。

如果我们能让 RNN 在接受上一时刻的状态和当前时刻的输入时，有选择地记忆和删除一部分内容（或者说信息），问题就可以解决了，比如有一句话提及刚才吃了苹果，那么在此之前说的吃香蕉的内容就没那么重要，删除就好了。

在各种博客和技术文档中，都有很多种 LSTM 的表现形式，每一种都有其特点。为了便于理解，我按照下图的形式绘制了 LSTM 的结构图：

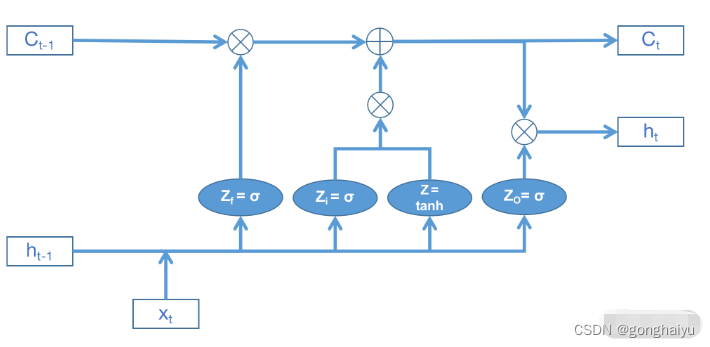
RNN 只维持 1 个传递状态，LSTM 则需要维持 2 个传输状态。Ct-1表示上一时刻的细胞状态（cell state），ht-1则表示上一时刻的隐藏状态（hidden state）。

LSTM 独特的地方在于它内部使用了 3 个逻辑门来控制细胞的状态，分别是遗忘门、输入门和输出门，并对应了忘记、选择、更新、输出这 4 个不同的阶段，从而有选择性地保留或删除信息。我们来具体看一下。

忘记阶段：刚才说过，对于上一时刻的状态我们如果能够选择性地记忆就好了。LSTM 中就使用了 Zf这个逻辑门来实现相应的功能，比如我们阅读一篇小说，我们会更倾向于忘记景色描写而不是人物对话，因为它并没有太多用途。这个逻辑门实际上是一个 Sigmoid 单元，我们称为遗忘门。Sigmoid 可以将输入映射在 0～1 之间，得到的值再与 Ct-1相乘，这样就实现了对上一时刻状态 Ct-1的控制，即哪些信息保留或者删除多少。遗忘门的公式化表示为：

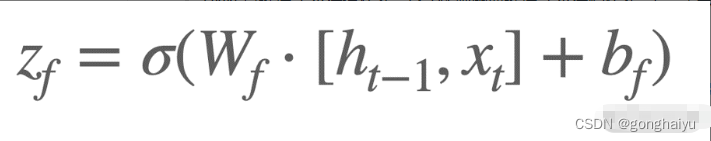
选择阶段：忘记阶段用来选择性保留或者删除上一时刻的内容，那当前时刻的输入呢？我们也需要类似的处理单元来进行选择，或者说决定给细胞状态添加哪些新的信息。这个阶段包括 2 个环节：首先是利用 ht-1和 xt通过 1 个 Sigmoid 单元决定更新哪些信息，然后利用 ht-1和 xt通过 1 个 tanh 层得到新的候选细胞信息，这些信息会根据计算的结果更新到细胞中。这个过程就是输入门，公式化表示为：

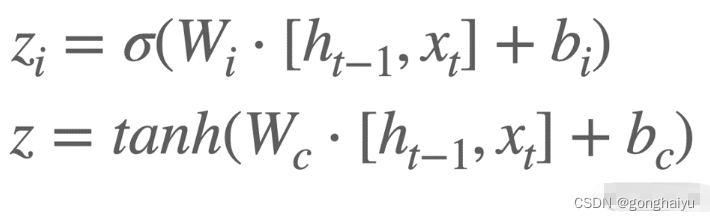
更新阶段：经过选择阶段我们确定了当前时刻输入的信息哪些需要留下，接下来就要对细胞状态 C 进行更新了。这个环节实际上就是把前 2 个环节得到的结果与对应的信息相乘后再加起来，其公式化表示如下：

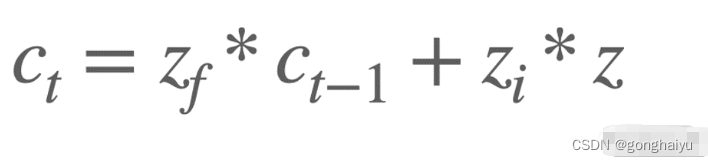
我们可以到这个公式的平衡美：zf 和 zi 分别控制了上个阶段和当前阶段要保留多少内容，ct-1 和 zi 则是上个阶段和当前阶段的内容本身，所以是一个非常灵活的控制方式。

输出阶段：更新完细胞的状态，就到了最终的输出环节。这个过程中还是需要 ht-1 和 xt 的参与，这 2 个信息经过一个叫输出门的 Sigmoid 逻辑单元后，与经过 tanh 后被缩放到-1～1 之间的细胞状态 Ct 信息相乘，就得到了当前时刻的隐藏状态 ht。得到 ht 之后，就能得到当前时刻的输出 y 了。ht 的计算过程如下：

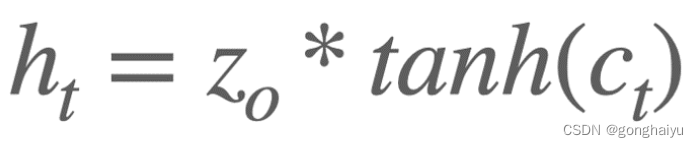
LSTM 在过去的一段时间里都有着广泛的应用，比如音乐创作、股票价格预测等与时间序列相关的问题，并且在 NLP 问题上也表现良好。但正因为它侧重时间序列以及其本身的结构特点，LSTM 也有着非常明显的缺点，我列举了其中 3 点，如下：

1. 并行化困难。LSTM 的本质是一个递归的训练过程，随着实际问题的愈发复杂，这个缺点就会越来越致命。
2. 梯度消失。LSTM 虽然在一定程度上缓解了 RNN 的问题，但是对于长序列的情况，仍有可能会出现梯度消失。
3. LSTM 在计算的时候需要的资源较多。

这些缺点意味着 LSTM 在未来的应用可能会逐步减少，同时，在不同的问题上已经出现了更好的解决方案，例如在 NLP 问题中被广泛采用的 Transformer 框架。

自编码器

深度学习中大部分能落地的项目都属于有监督学习。有监督学习的特点就是每个训练数据都有一个已知的标签。无监督学习则是在没有额外信息的情况下自动提取数据中模式和结构。有监督学习和无监督学习最大的区别就在于，有监督学习的训练集是需要人工提前标记的。这一讲，我要介绍的自编码器则是无监督学习的一个应用。

自编码器

自编码器是一个无监督的应用，它使用反向传播来更新参数，它最终的目标是让输出等于输入。数学上的表达为，f(x) = x，f 为自编码器，x 为输入数据。

在这个过程中，自编码器会先将输入数据压缩到一个较低维度的特征，然后利用这个较低维度的特征重现输入的数据，重现后的数据就是自编码器的输出。所以，从本质上来说，自编码器就是一个压缩算法。
一个自编码器由 3 个部分组成：

1. 编码器（Encoder）：用于数据压缩。
2. 压缩特征向量（Compressed Feature Vector）：被编码器压缩后的特征。
3. 解码器（Decoder）：用于数据解码。

自编码器的结构如下图所示：

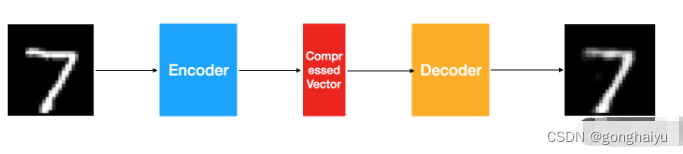
对自编码器我要做如下 3 点说明：

1. 自编码器只能压缩与训练数据相似的数据。比如我们用 MNIST 训练自编码器，那它只能压缩手写数字相关的数据，如果用来压缩手写数字以外的数据，表现就会很差；
2. 自编码器解压缩的结果只能接近输入，并不完全一样。所以，换句话说，它是一个有损的压缩算法；
3. 自编码器是一个无监督学习的算法。训练一个自编码器，我们不需要对数据做任何标注，只需要把原始数据扔给它就可以了，它会自动挖掘数据中的潜在结构模式。

自编码器的网络架构

压缩特征向量也是人工神经网络中的一层，它的维度就是我们要将数据压缩到的维度，是一个超参，我们要提前设定。

下图是一个详细的自编码器的网络结构。

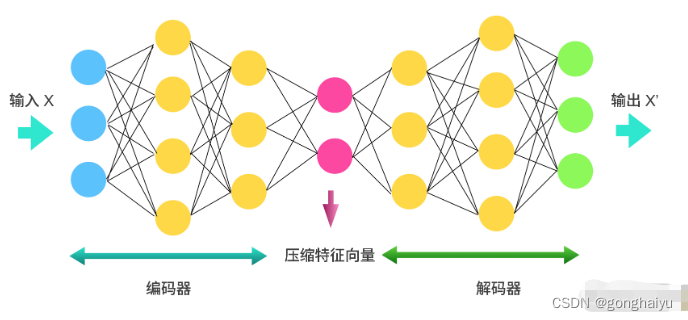
从图中可以看到，首先我们会有 3 个维度的输入 x 通过编码器，然后生成 1 个有两个维度的压缩特征向量。解码器会将这两个维度的特征向量恢复到 3 个维度的 x’，然后输出。

整个过程的宗旨只有一个：输出的 x’无限接近输入 x。

对于一个自编码器，会有 3 个超参需要设定：

1. 压缩特征向量的神经元的个数，也就是压缩后的维度。神经元的个数越少则代表有更重的压缩。
2. 层的个数。自编码器的结构可以按照我们的想法任意设定。
3. 每一层中神经元的个数。

我们现在介绍的这种自编码器是一层层堆叠起来的，所以又可以称为堆叠式自编码器。通常来说，堆叠式自编码器的结构总体上看起来像一个三明治，编码器与解码器是对称的。从输入到中间的压缩特征向量，神经元的个数逐层减少；从中间的压缩特征向量到输出层，神经元的个数逐层递增。

自编码器的实现

接下来，我们看看具体怎么构建一个自编码器。总体上而言，如何训练一个自编码器呢？只需要以下几个步骤：

1. 构造一个编码器和解码器；
2. 设定一个损失函数来衡量输出 x’与输入 x 的差距；
3. 选择一个优化方法，来更新参数，例如 SGD。

我们把上面 3 步再具体一些。

1. 我们有数据集 D：D={x1,x2,…,xi,…,xm}，其中 xi=(xi,1,xi,2,…,xi,n)。
2. 编码器为 y=h(x)，y 是上图中的压缩特征向量。
3. 解码器为 x’=f(y)=f(h(x))。
4. 如果输入的数据是数值型，则利用均方误差（MSE）来衡量输出 x’与输入 x 之间的差距；如果输入的数据是离散型，则利用交叉熵损失来衡量输出 x’与输入 x 之间的差距。
5. h(x)与 f(y)的参数会通过我们设定好的优化方法进行更新。

下面我们用 MNIST 数据来训练一个下图这样的自编码器：

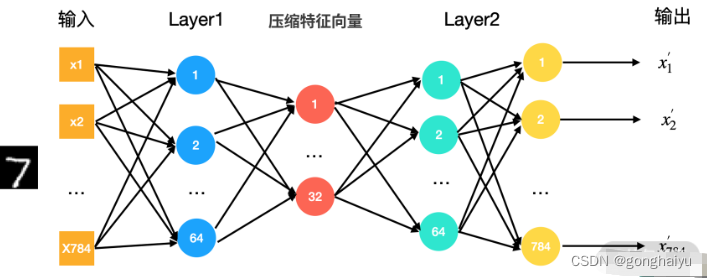
因为我们还没有学习到 TensorFlow 编程，所以这里先使用 Keras 举例。Keras 的优点是代码非常简单且易读性高。
我们的代码中会用到 Keras 的 Dense 模块，Dense 就是一个全连接层。如果你对 Keras 很感兴趣，可以点击链接查看。

下面我们来看一下图中自编码器的实现，我在代码中已经写好了注释：

# 输入的大小。

# 因为输入的图片 shape 是(28, 28)，将它展开后的大小是 784

input_size = 784

# 隐藏层神经元的大小

hidden_size = 64

# 压缩向量长度为 32

compression_size = 32

# autoEncoder 网络定义

# 输入层

input_img = Input(shape=(input_size,))

# 隐藏层 Layer1

hidden_1 = Dense(hidden_size, activation='relu')(input_img)

# 压缩特征向量

compressed_vector = Dense(compression_size, activation='relu')(hidden_1)

# 隐藏层 Layer2

hidden_2 = Dense(hidden_size, activation='relu')(compressed_vector)

# 输出层

output_img = Dense(input_size, activation='sigmoid')(hidden_2)

# 网络训练

autoEncoder = Model(input_img, output_img)

autoEncoder.compile(optimizer='adam', loss='binary_crossentropy')

autoEncoder.fit(x_train, x_train, epochs=3)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44

通过以上代码，我们从输入层、隐藏层到输出层，构建了一个最为简单的自编码器。

然后，我们用刚才训练的自编码器测试一下 MNIST 测试集的前 6 张图片。可以发现，解码后基本可以恢复到原图的效果。

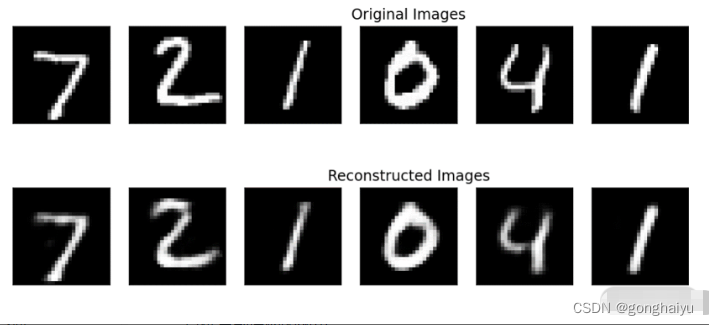
通过刚才的代码我们可以发现，自编码器的网络结构非常容易控制，只要增加网络的层数、每一层的节点数以及压缩向量的长度就让网络变得更加强大。

增加这些超参会让自编码器学习到更加复杂的压缩编码模型，但同时也会带来一定的问题。太复杂的网络有可能让网络变得非常容易过拟合，并且网络也很难学习到输入数据的潜在特征，只会学到将输入数据拷贝到输出这样一种单纯的恒等变换。

模型过拟合的时候，在训练集上会有非常优秀的表现，但是遇到训练集以外的数据就不会有很好的效果。这就是为什么我们大部分自编码器都是三明治结构，并且故意保留了一个比较小的压缩特征向量。

那除了保留一个较小的压缩特征向量之外，还有没有其他方法可以让自编码器更加专注地发现数据中的潜在结构呢？

那就是我接下来要介绍的两种方式，降噪自编码器与稀疏自编码器。

降噪自编码器（Denoising AutoEncoders）

降噪自编码器是在训练时，在输入的数据中加入随机噪音，在最后输出的时候恢复到没有噪音的状态的一种编码器。

因为输入的数据中加入了随机噪音，就避免了网络只学习到简单的将输入复制到输出的这种恒等变换，强制让自编码器学习如何剔除数据中的噪音，然后再恢复到没有噪音的状态。这样就能让它更加专注地挖掘数据中的潜在结构模式。

我们依然使用 MNIST 来举例，我在训练数据中加入了随机的噪音，如下图所示：

训练时，我们把第二行图片作为输入，第一行的原始图片作为输出。在代码上，降噪自编码器的训练只有一点与普通的自编码器不一样，就是输入数据的选择。

我们使用上文介绍的网络结构来训练，但是请你注意，fit 的时候，输入变成了 x_train_noisy。

# denoising autoEncoder 的网络结构

# 与上一个例子中的网络结构一样

input_img = Input(shape=(input_size,))

hidden_1 = Dense(hidden_size, activation='relu')(input_img)

compressed_vector = Dense(compression_size, activation='relu')(hidden_1)

hidden_2 = Dense(hidden_size, activation='relu')(compressed_vector)

output_img = Dense(input_size, activation='sigmoid')(hidden_2)

autoEncoder = Model(input_img, output_img)

autoEncoder.compile(optimizer='adam', loss='binary_crossentropy')

autoEncoder.fit(x_train_noisy, x_train, epochs=3)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20

通过上述代码，我们实现了降噪自编码器。
下面我们来可视化一下，看看降噪编码器是否可以生成没有噪音的图片。

从结果上看，效果还是不错的。最下面一行是自编码器的输出，自编码器成功去除了噪音，还原了图片的本来面貌。

稀疏自编码器（Sparse AutoEncoders）

我们已经学习了 2 种让自编码器学习到有用特征的方法：保持较小的压缩特征向量和降噪自编码器。下面我来介绍第 3 种方法，稀疏自编码器。

我们可以通过限制自编码器中神经元的输出，只让很小的一部分神经元有非 0 的输出，也可以说是只激活一小部分的神经元。这就迫使自编码器将输入与一部分节点联系起来，从而让它发现数据中更有价值的结构。即使压缩特征向量中有很多节点，有这种约束的自动编码器也可以很好地工作，因为它只让一部分节点被激活。

具体怎么做呢？我们只需要在损失函数中加一个惩罚项，在训练时就可以让自编码器只有一小部分节点被激活，这样我们就得到一个稀疏自编码器了。

那么现在要考考你了，你还记得什么样的正则约束会实现这种稀疏的约束吗？答案是我们在第 1 讲中介绍的 L1 范数。我们这里讲的稀疏自编码器在 Keras 中也很好实现。参考链接：https://keras.io/zh/layers/core/

之前我们是用如下的方式建立的全连接层：

hidden_1 = Dense(hidden_size, activation='relu')(input_img)

1
2

我们现在添加一个叫作 activity_regularizer 的参数，它可以对层的输出进行正则化约束。约束的方式我们选择的是 L1 正则化。L1 正则化的参数一般会是在[0.001, 0.000001]这个范围内，我们选择 0.0001。

hidden_1 = Dense(hidden_size, activation='relu', activity_regularizer=l1(0.0001))(input_img)

1
2

接下来我们训练 2 个自编码器。

1. 标准的自编码器：与上文介绍的一样。
2. 稀疏自编码器：在压缩特征向量那一层增加 L1 正则约束。

然后对比一下压缩特征向量的输出分布。

我们通过下面的代码获得标准自编码器与稀疏自编码器压缩特征向量的输出。

standard_scores = Encoder_autoEncoder.predict(x_test).ravel()

sparse_autoEncoder = Encoder_sparse_autoEncoder.predict(x_test).ravel()

1
2
3
4

然后绘制一下它们的概率密度图，如下所示：

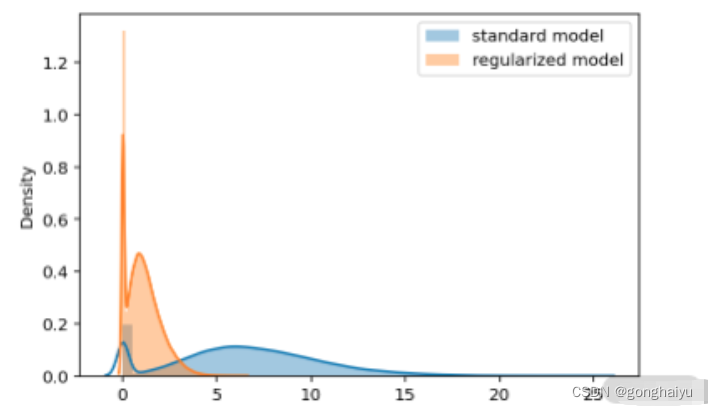
可以发现，我们的 L1 正则约束确实对压缩特征向量起到了效果，大部分时候的输出都是 0。而标准的自编码器的压缩特征向量的输出相对平缓一些。

非常不幸地告诉你，自编码器并没有被广泛地应用在现实世界中。所以自编码器主要有以下两个用途：

1. 数据降噪。
2. 降维处理。
   自编码器常用于降维处理，它的降维性能要强于主成分分析（Principal Component Analysis, PCA）。PCA 只能做线性变换，而自编码器可以做非线性变换，可以发现数据中更多有趣的事情。