手把手教你用C语言实现求质数（素数），5大方法任君挑选_素数c语言程序编写

什么是质数（素数）？

质数又称素数。一个大于1的自然数，除了1和它自身外，不能被其他自然数整除的数叫做质数；否则称为合数（规定1既不是质数也不是合数）。———来自百度百科

第一种方法，暴力解决

我们设定一个数为x，根据质数的定义判断x是否为质数，我们看它能否被2、3、4······、x-1整除，如果它不能被其中任何一个整数整除，则这个数就是质数。
比如要判断11是不是质数，我们就看能否被下面这10个数整除。
2、3、4、5、6、7、8、9、10
因为11无法被其中任何一个数整除，则判断它为质数。

如果我们要找1—1000内的质数，我们可以控制x从2自己增到1000，并且x每次自增1过后，都要从2开始找能否被x所整除的数，直到找不到结束。所以我们可以用两层for循环来控制，第一层来控制x产生2–1000数字，第二层for循环产生2到x-1的数，并且判断能否被整除。（因为1不是质数，把1排除在外）

并且我还设置了一个计数器count来统计大概运算的次数，方便和下面方法做对比。代码如下：

//求1--1000内的质数（素数）
#include <stdio.h>
int main()
{
	int x = 0;   
	int i = 0;
	unsigned int count = 0;  //统计运算的次数
	for (x = 2; x < 1000; x++)    //在2到1000之间找质数
	{
		for (i = 2; i < x; i++)   //试除法，能不能被x整除，从2开始找，直到等于x
		{
			count++;
			if (x % i == 0)   //找到能被x整除的数了
			{
				break;
			}
		}
		if (x == i)   //找到和x相等也没有被整除的，证明是质数
		{
			printf("%d ",x);
		}
	}
	printf("\n\n\n");
	printf("运算的次数：%d ",count);
	return 0;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27

第一种方法运行结果：

第二种方法，用奇数

第一种方法是否有点复杂呢，这是当然的。
其实我们从质数：
2、3、5、7、9、11、13、17、19······中发现什么规律了没有呢？

嘿嘿嘿，那就是除了2以外那些2的倍数（4、6、8、10、12、14、18·······）都不是质数。

所以我们的第一层for循环是不是可以不用一步步自增1，而是从3开始自增2呢，从而产生3、5、7、9、11······这样就把偶数给巧妙避免了。代码如下：

#define _CRT_SECURE_NO_WARNINGS 1
#include <stdio.h>
int main()
{
	int x = 0;
	int i = 0;
	unsigned int count = 0;
	x = 2;
	printf("%d ",x);   //已经知道2为质数，所以先第一个打印
	for (x = 3; x < 1000; x += 2)  //从3开始自增2
	{
		for (i = 2; i < x; i++)
		{
			count++;
			if (x % i == 0)
			{
				break;
			}
		}
		if (x == i)
		{
			printf("%d ",x);
		}
	}
	printf("\n\n\n");
	printf("运算的次数：%d ", count);
	return 0;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28

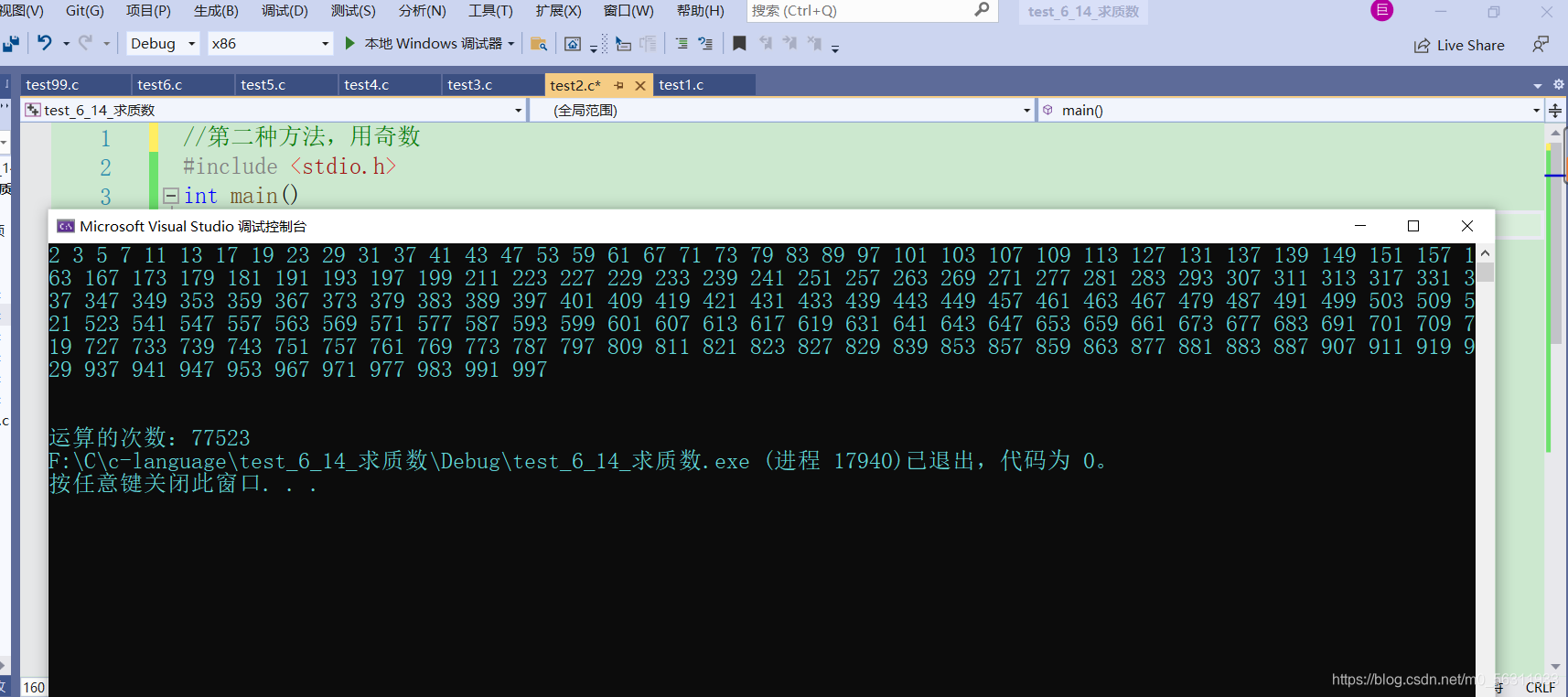
第二种方法运行结果：

第一种和第二种对比图片：

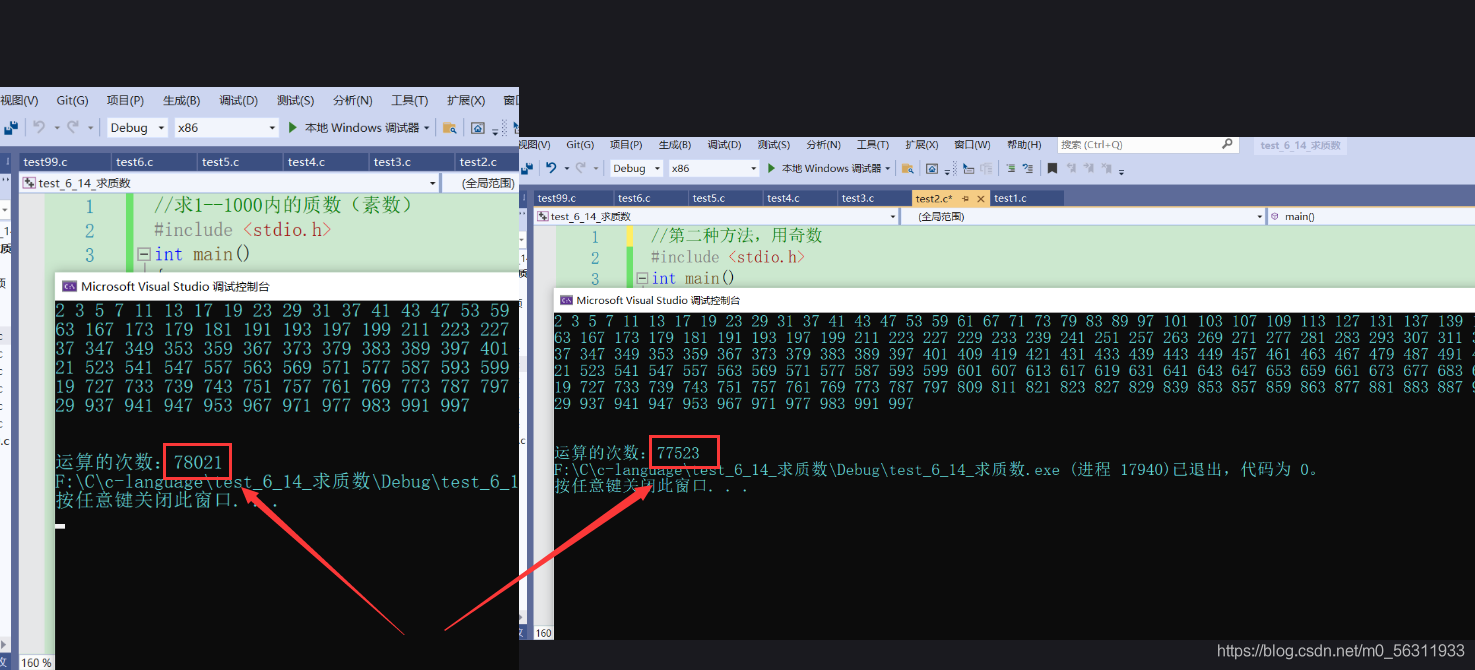
大家发现了没有好像第二种并没有比第一种运算要少很多，这个是因为当判断33、66、666这些在开始阶段i=3的时候，马上就可以判定不是质数了，所以运算次数并没有怎么减少。

第三种方法，奇数双管齐下

结合第二种方法，除了2以外那些2的倍数（4、6、8、10、12、14、18·······）都不是质数。
所以除了2以外质数一定是奇数。
从而判断11是否为质数的时候，我们不再需要判断能否被2、3、4、5、6、7、8、9、10这9个数整除，我们只需要判断 能否被3、5、7、9这几个数整除即可。
所以我们可以控制第二层for循环不再自增1，而是从3开始自增2。
代码如下：

#define _CRT_SECURE_NO_WARNINGS 1
#include <stdio.h>
int main()
{
	int x = 0;
	int i = 0;
	unsigned int count = 0;
	x = 2;
	printf("%d ",x);
	for (x = 3; x < 1000; x += 2)  //只产生奇数
	{
		for (i = 3; i < x; i += 2)  //只产生奇数
		{
			count++;
			if (x % i == 0)
			{
				break;
			}
		}
		if (x == i)
		{
			printf("%d ",x);
		}
	}
	printf("\n\n\n");
	printf("运算的次数：%d ", count);
	return 0;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28

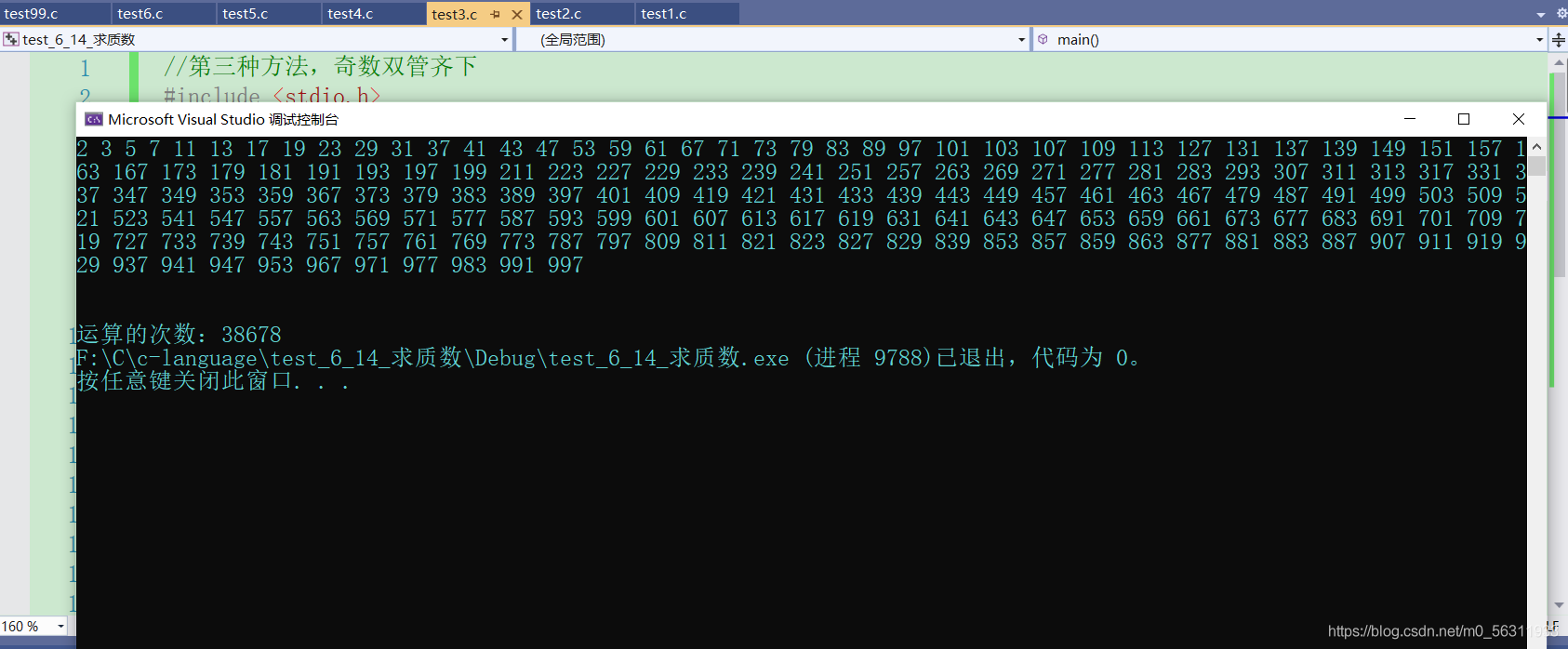
第三种方法运行结果：

第四种方法，巧用数组

在第三种的基础上再看，我们还发现如下规律：
不能被3整除的整数也无法被大于3的那些3的倍数（6、9、12······）整除。
不能被5整除的整数也无法被大于5的那些倍数（10、15、20······）整除。
所以，如果整数x无法被小于x的质数整除，那么x就是质数。
根据这个条件，我们求质数就有了另外一条思路：我们用数组来保存质数，控制x自增后，用x除去数组的每一个元素，如果不能整除则是质数，并且保存到数组中。

因此，我们先把2、3这两个质数保存到数组中，第一层for循环依旧是控制x自增，第二层for循环来遍历数组。遍历后如果都不能整除，则存到数组中。如果有一个能被整除，则不是质数，不保存。

代码如下：

#define _CRT_SECURE_NO_WARNINGS 1
#include <stdio.h>
int main()
{
	int arr[500] = { 0 };
	int x = 0;
	int i = 0;
	unsigned int count = 0;
	int sum = 0;  //定义数组的下标
	arr[sum] = 2;  //把2存到数组中
	sum++;
	arr[sum] = 3;   //把3存到数组中
	sum++;
	for (x = 5; x < 1000; x += 2)
	{
	  //从下标0开始遍历，直到数组的最后一个质数
		for (i = 0; i < sum; i++ ) 
		{
			count++;
			if (x % arr[i] == 0)
			{
				break;
			}
		}
		if (sum == i)  //遍历后都不能整除
		{
			arr[sum] = x;  //把质数保存到数组中
			sum++;   //下标加1，为下次放做准备
		}
	}
	for (i = 0; i < sum; i++)
	{
		printf("%d ", arr[i]);
	}
	printf("\n\n\n");
	printf("运算的次数：%d ", count);
	return 0;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38

运算结果：

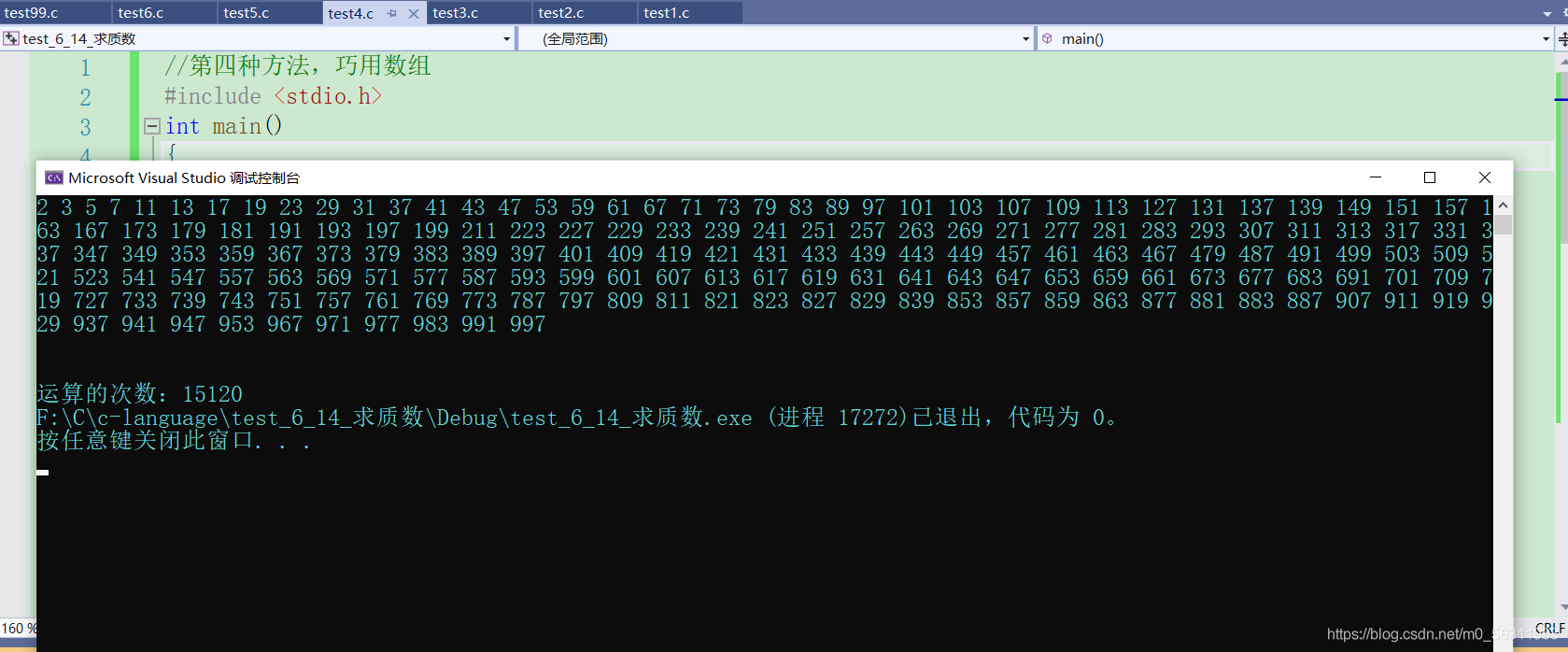
第五种方法，巧用平方根

写法1：

我们设两个整数a和b，如果不是质数的话，整数x就可以写成 x=a * b 比如：
36=2 * 18
36=3 * 12
36=4 * 9
36=6 * 6
如果整数x为质数，那么就不可能写成 x = a * b的形式。所以如果整数x无法被小于等于x的平方根的质数整除，则x为质数。
因此，我们可以在第四种方法上改造一下，就是在第二层for循环，从数组的第一个元素出发，每一个都写成平方，直到平方大于整数x退出循环。
代码如下：

//第五种方法，巧用平方根,写法1：
#include <stdio.h>
int main()
{
	int arr[500] = { 0 };
	int x = 0;      //定义要找质数的变量
	int i = 0;
	unsigned int count = 0;
	int sum = 0;    //定义数组下标
	arr[sum] = 2;  //2是质数，储放到数组中
	sum++;
	arr[sum] = 3;   //3也是质数，放到数组中
	sum++;
	for (x = 5; x < 1000; x += 2)   //只查找奇数
	{
		for (i = 0;arr[i] * arr[i] <= x; i++)   //利用数组中的元素平方去排查
		{
			count++;
			if (x % arr[i] == 0)   //不是质数
			{
				break;
			}
		}
		if (arr[i]*arr[i]>x)     //为质数
		{
			arr[sum] = x;   //把找到的奇数放到数组中
			sum++;          //下标加1
		}
	}
	for (i = 0; i < sum; i++)
	{
		printf("%d ",arr[i]);
	}
	printf("\n\n\n");
	printf("运算的次数：%d ", count);
	return 0;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37

运算结果：

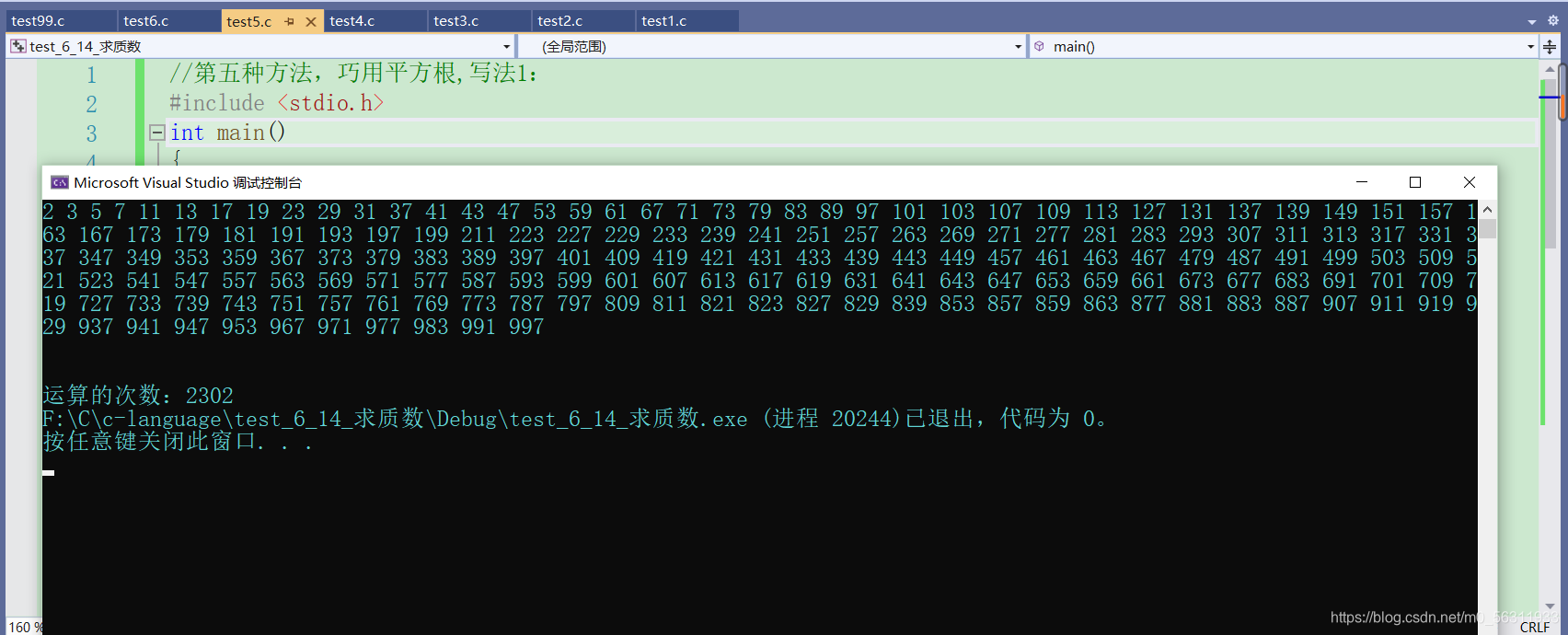
写法2：

我们不要数组也可以，直接在第三种方法上改造。
代码如下：

//第五种方法，巧用平方根,写法二：
#include <stdio.h>
int main()
{
	int x = 0;
	int i = 0;
	unsigned int count = 0;
	x = 2;
	printf("%d ",x);
	for (x = 3; x <= 1000; x += 2)
	{
		for (i = 2; i*i<=x; i++)  //控制第二层循环
		{
			count++;
			if (x % i == 0)
			{
				break;
			}
		}
		if (i*i>x)
		{
			printf("%d ",x);
		}
	}
	printf("\n\n\n");
	printf("运算的次数为：%d ",count);
	return 0;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28

运算结果：

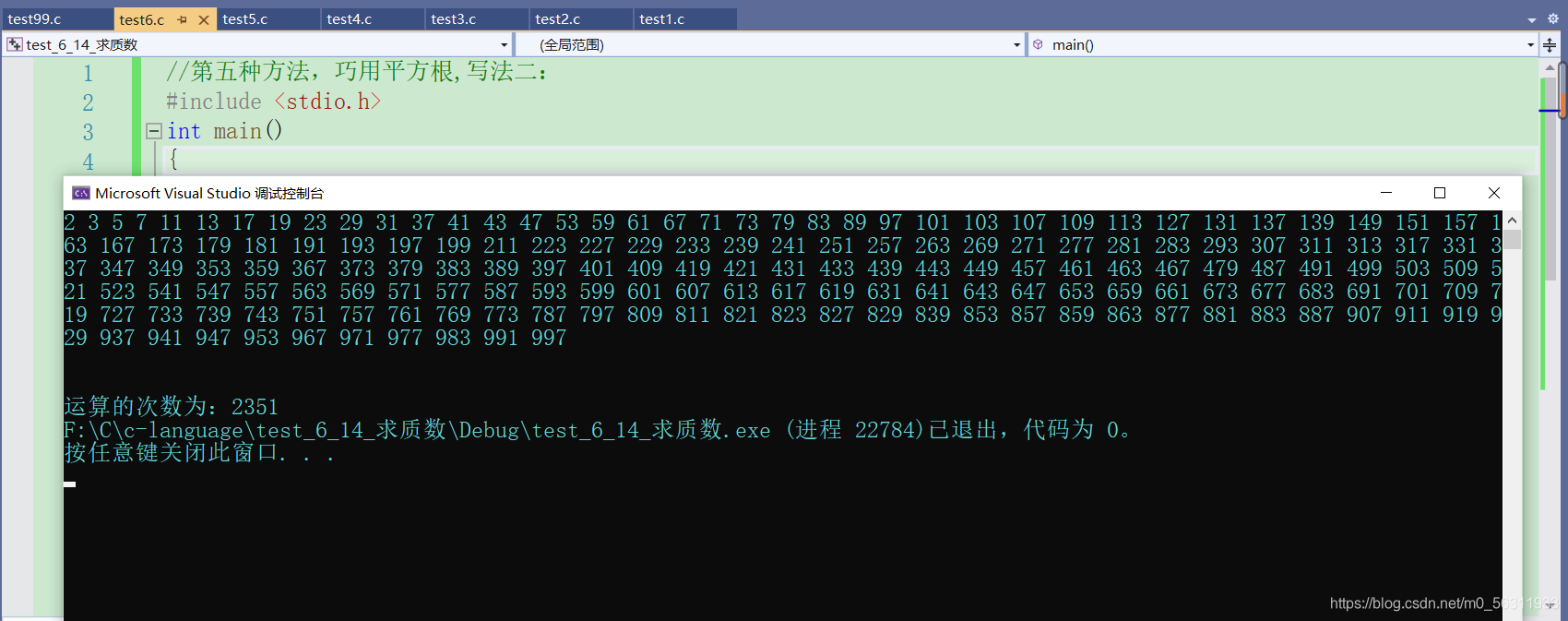
总结

我们从第一种的简单粗暴到最后的优良改造，运算次数一步步地减少，大家是否领悟到了编程的优美了呢？我特别推荐最后一种的写法二，既不用数组，也可以节省很多的运算时间。

如果有错误的地方，还有改进的方法，欢迎在评论区指出。

既然都看到这里了，点个赞呗，嘿嘿嘿。