美赛（三）——E题_历年美赛e题题目

通径分析

使用背景

大前提：所有变量都要服从正态分布

• 仅仅研究两个变量的关系

  简单相关系数(皮尔逊相关系数)

• 多个相关变量中研究两个变量之间的关系

  偏相关系数(注意，多个变量之间应该是相关的)

• 多个不相关自变量与一个因变量之间的关系

  多元回归

• 多个相关的自变量与一个因变量之间的关系

  通径分析

• 多个相关的因变量和多个相关的自变量之间的关系

  典型相关系数

数学原理

先做一个r检验(相关性检验)？
如果用到通径分析，一定要把这个线性表达式公式写到文章里去

计算步骤

• 1.计算所有自变量与因变量的简单相关系数，并做相关性检验，排除与因变量不相关的自变量。
• 2.计算余下所有自变量之间的相关系数。
• 3.建立通径方程。
• 4.解方程组，计算出直接通径系数

典型相关分析

适用对象

  多个相关的因变量和多个相关的自变量之间的关系

• $u_1,u_2,u_3...各自线性无关$
• $v_1,v_2,v_3...各自线性无关$
• $u_1$只与$v_1$相关，与其他的$v$不相关（以此类推）
• $v_1$只与$u_1$相关，与其他的$u$不相关（以此类推）
• 具有最大相关性的一对称为$u_1,v_1$,具有第二大相关性的便是$u_2,v_2$(以此类推)
• 约束条件：$u_k$和$v_k$的方差均为1

例：

  解释问题：哪一个x与哪一个y关系紧密
  运行结果：


  文章里提及：

• 典型相关：三对典型变量的相关系数
• 特征值：没有任何特殊意义，但要写，还要写比例
• F值
• 自由度
• Pr>F(也叫F检验的显著性概率)：概率小于0.05，拒绝原假设，说明对应的典型变量是相关的
    上图中，前两对典型变量的显著性概率都小于0.05，说明前两对典型变量是相关的。第三对典型变量线性关系不显著。因此，只留下前两对典型变量。
  
  
• 产出组与影响组典型相关系数平方：对应典型R方（VAR或WITH都可）
• 对产出组解释能力：对应VAR-它们自己-比例
• 产出组方差被影响组典型变量解释比例：对应VAR-对立面-比例

对上述表格的解释:

• $v_1$中，$y_1$和$y_2$占的权重比较大；$w_1$中，$x_1$占的权重比较大；而$v_1$和$w_1$还具有较高的相关系数，因此，$x_1$和$y_1$与$y_2$关系很紧密，也就是说，$x_1$是首先影响$y_1$与$y_2$的
• $v_2$中，$y_1$和$y_2$占的权重比较大；$w_2$中，$x_2$占的权重比较大；而$v_2$和$w_2$还具有比较高的相关系数，因此，$x_2$和$y_1$与$y_2$关系很紧密，也就是说，$x_2$是首先影响$y_1$与$y_2$的

Bayes判别法

  判别分析是一种在一些已知研究对象用某种方法已经分成若干类的情况下，确定新的样品的观测数据属于哪一类的统计分析方法。
  目前比较流行的判别方法：贝叶斯判别，Fisher判别，模糊识别，神经网络，支持向量机，距离判别法，逐步判别法。

使用前提

• 数据符合正态分布

基本思想

  总是假设对所研究的对象已有一定的认识，计算新给样品属于各总体的条件概率$P(G_i|x_0),(i=1,...k)$比较这个概率的大小，然后将新样品判归为来自概率最大的总体。
  设有总体$G_i(i=1,2,...,k)$,$G_i$具有概率密度函数$f_i(x)$.并且根据以往的统计分析，知道$G_i$出现的概率为$q_i$。即当样本$x_0$发生后，求他属于某类的概率。由贝叶斯共识计算后验概率，有
$$P(G_i|x_0)=\frac{q_i{f}_i(x_0)}{\sum q_i{f}_i(x_0)}$$
  判别规则：若
$$P(G_h|x_0)=maxP(G_i|x_0)(1\le i\le k)$$
  则$x_0$判给$G_h$

一般步骤

• 1.计算各类中变量的均值${\bar{x}}_j$及均值向量${\bar{x}}_h$($h=1,2,...k$),各变量的总均值${\bar{x}}_j$($j=1,2,...p$)及均值向量
• 2.计算类内协方差矩阵S及其逆矩阵S-1 ；
• 3.计算Bayes判别函数中，各个变量的系数及常数项并写出判别函数；
• 4.计算类内协方差矩阵W及总各协方差矩阵T作多个变量的全体判别效果的检验；
• 5.各个变量的判别能力的检验；
• 6.判别新样本应属于的类别

例题

  数据如下：

  代码解释：

写作体现

• 1.写贝叶斯判别函数

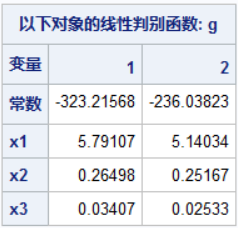
  注意：这些系数要与回归区别开，这些系数没有特别的意义，只是作为函数的系数
  判别方法：将每个国家所给的参数代入，比较y1与y2的大小，谁大，就是哪一类
  一般而言，得出判别公式后要对原有的数据进行判别，判别错误的概率称为误判率，SAS会计算出来


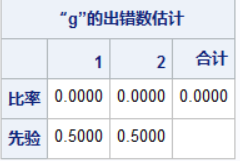
  可以看到，第一类的误判概率为0，第二类的误判概率为零，合计误判概率也为零，说明我们创建出来的判别函数很有效，判别能力很强
  贝叶斯判别工作中规定先验概率为类别个数分之一
  
  之后判别新数据：

  解释：

• _1:y1/(y1+y2)

• _2:y2/(y1+y2)

• 2.将原有数据重新判别一下

• 3.进行现有数据的判别，并给出自己可能认为的原因

逐步判别法

背景

  在判别问题中，当判别变量个数较多时，如果不加选择地一概采用来建立判别函数，
不仅计算量大，还由于变量之间的相关性，可能使求解逆矩阵的计算精度下降，建立的判别函数不稳定。因 此适当地筛选变量的问题就成为一个很重要的事情。凡具有筛选变量能力的判别分析方法就统称为逐步判别法。

基本思想

  逐步判别法其基本思路类似于逐步回归分析，按照变量是否重要逐步引入变量，每引入一个“最重要”的变量进入判别式，同时要考虑较早引入的变量是否由于其后的新变量的引入使之丧失了重要性变得不再显著了（例如其作用被后引入地某几个变量的组合所代替），应及时从判别式中把它剔除，直到判别式中没有不重要的变量需要剔除，剩下来的变量也没有重要的变量可引入判别式时，逐步筛选结束。也就是说每步引入或剔除变量，都作相应的统计检验，使最后的判别函数仅保留“重要”的变量。

步骤

• 1.计算各总体中各变量的均值和总均值以及似然统计量，规定引入变量和剔除变量的临界值F进、F出。
• 2.逐步计算，计算全部变量的判别能力，在已入选变量中考虑剔除可能存在的最不显著变量。在未选入变量中选出最大判别能力的变量，对变量作F检验通过检验则接受，否则剔除变量。直到能剔除又不能增加新变量，逐步计算结束。
• 3.建立判别式，使用第2步中选入的变量，用Bayes判别法建立判别式。
• 4.对待判样本进行判别分类。

例题及代码分析

  例题还是引用上面的人文系数作为参数
  先注释掉下面的代码，运行一遍结果

• Pr>F：（该程序的显著性水平是0.30）x3对应的概率为0.0004，原假设是该变量不重要，0.0004小于0.30，小概率事件发生，说明x3很重要；x1对应的概率为0.1516，原假设是该变量不重要，0.1516小于0.30，小概率事件发生，说明x1很重要；
• 显著性水平越小（标准越高），留下的变量越小
• 作图的时候留下step；number in；entered；F value；Pr>F这几列

  之后将下面的注释恢复，将上面的代码注释掉

  运行代码：


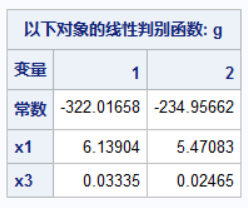
  看一下新判别函数的误判率


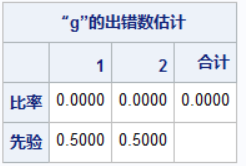
  两类的误判率均为0，说明判别能力很强
  评估待判别数据


因子分析

简要介绍

• 需要先把$x_i$标准化
• ${\epsilon }_i$是特殊因子（每个变量所拥有的别人没有的东西）
• $F_m$每个变量所共有的东西（公因子），公因子之间彼此应该是线性无关的

一般步骤

例题

• 做综合评价时，先把数据处理为同向化

结果分析

  要求因子累计贡献率超过80%，结果表明要选取2个因子，即前两个

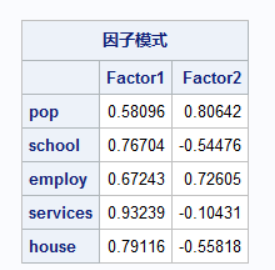
  采用因子旋转

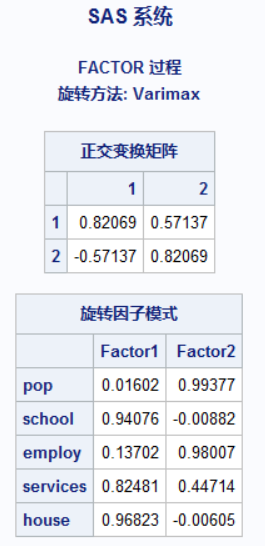
• 第一公因子与school，services，house关系紧密
• 第二公因子与pop，employ关系紧密
• 猜测第一公因子为福利因子
• 猜测第二公因子为经济因子

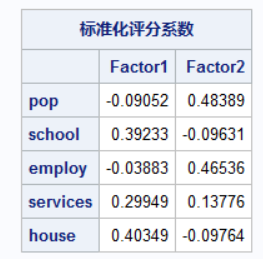
  得到两个因子得分向量


  根据因子得分表：

• 10，1，4的福利因子较大，即福利水平高
• 12，10，11的经济因子较大，即经济水平高

  做综合评价的方法：将最后两列分别乘以相应的贡献率（0.5747，0.3593），得出最终得分