Guff_9hys

这个屌丝很懒，什么也没留下！

热门标签

数据结构入门-6-二叉树_二叉树叶子节点

作者：Guff_9hys | 2024-06-22 22:16:12

踩

二叉树叶子节点

一.树结构

在这里插入图片描述
为什么要用树结构?

将数据使用树结构存储后,出奇的高效

二分搜索树(Binary Search Tree)
平衡二叉树:AVL;红黑树
堆;并查集
线段数;Trie(字典数,前缀树)

1.2 数的性质

树中的节点数 = 所有节点的度数之和+1

n = n0 + n1 + n2 + n3 = n1 + 2n2 + 3n3 + 1
1

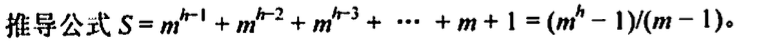
在这里插入图片描述

二. 二叉树(多叉树)

在这里插入图片描述

class Node { 
	E e;
	Node left;
	Node right;
}
1
2
3
4
5

二叉树具有唯一的根节点
左孩子右孩子
二叉树中每个节点最多有两个孩子
叶子节点:没有孩子的节点
二叉树每个节点最多只有一个父亲节点

====================================================

二叉树具有天然的递归结构
- 左子树每个节点的左子树也是二叉树
- 右子树每个节点的右子树也是二叉树
二叉树不一定是满的
- 一个节点也可以是二叉树
- NULL也可以是二叉树

天然地柜结构

2.2 二叉树的性质

叶子节点个数 = 度为2的节点个数 + 1：n0 = n2 + 1

n = n0 + n1 + n2

B:分支数
B + 1 = n ----> B = n - 1 -----> B = n0 + n1 + n2 - 1
B = 2n2 + n1
n0 + n1 + n2 - 1 = 2n2 + n1 ----> n0 = n2 + 1
1
2
3
4
5
6

当n位奇数时，n1 = 0；当n位偶数时，n1 = 1

当n位奇数时 n1 = 0；
	n = n0 + n1 + n2 
		= n0 + 0 + (n0-1)
		= 2n0 - 1
当n位偶数时，n1 = 1
	n = 2n0
1
2
3
4
5
6

h = log2(n+1)

三. 二分搜索树

Binary Search Tree 排序后的二叉树

在这里插入图片描述

条件

存储的元素具有可比较性,因为需要排序

public class BST<E extends Comparable<E>> {

    private class Node {
        public E e;
        public Node left, right;

        public Node(E e) {
            this.e = e;
            left = null;
            right = null;
        }
    }

    private Node root;
    private int size;

    public BST(){
        root = null;
        size = 0;
    }

    public int size(){
        return size;
    }

    public boolean isEmpty(){
        return size == 0;
    }

//向BST中添加新元素
    public void add(E e){
        if(root == null){
            root = new Node(e);
            size++;
        }

    }



    //向以node为root的BST插入e，递归
    private void add(Node node,E e){
        //终止条件
        if(e.equals(node.e))
            return;
        else if(e.compareTo(node.e) < 0 && node.left == null){
            node.left = new Node(e);
            size++;
            return;
        }
        else if(e.compareTo(node.e) > 0 && node.right == null){
            node.right = new Node(e);
            size++;
            return;
        }

        //递归调用
        if(e.compareTo(node.e) < 0)
            add(node.left,e);
        if(e.compareTo(node.e) > 0)
            add(node.right,e);
    }

}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64

3.2 BST add elements

以上的逻辑在root中添加 e 需要单独处理，可以进行改进

    public void add(E e){
        root = add(root,e);
    }

    //向以node为root的BST插入e，递归
    //返回添加的新Node
    private Node add(Node node,E e){
        //终止条件
        if(node == null){
            size ++;
            return new Node(e);
        }

        //递归调用
        if(e.compareTo(node.e) < 0)
            node.left = add(node.left,e);
        else if(e.compareTo(node.e) > 0)
            node.right = add(node.right,e);
        //== 情况不处理 直接丢弃

        return node;
    }   
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22

3.3 BST search elements

    //TODO 查找元素e
    public boolean contain(E e){
        return contain(root,e);
    }

    private boolean contain(Node node,E e){
        if (node == null) {
            return false;
        }
        if (e.compareTo(node.e) == 0) {
            return true;
        } else if (e.compareTo(node.e) > 0) {
            return contain(node.right,e);
        }else { //e.compareTo(node.e) < 0
            return contain(node.left,e);
        }
    }
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17

3.4 Order 遍历深度

前序遍历中序遍历后续遍历
都是深度优先的遍历

3.4.1 preOder

    //TODO Order
    //1 preOrder
    public void PreOrder(){
        PreOrder(root);
    }

    private void PreOrder(Node node){
        if (node == null) {
            return;
        }
        System.out.println(node.e);
        PreOrder(node.left);
        PreOrder(node.right);
    }
1
2
3
4
5
6
7
8
9
10
11
12
13
14

3.4.2 inOder

    //2 inOrder
    public void InOrder(){
        InOrder(root);
    }

    private void InOrder(Node node){
        if (node == null) {
            return;
        }
        InOrder(node.left);
        System.out.println(node.e);
        InOrder(node.right);
    }
1
2
3
4
5
6
7
8
9
10
11
12
13

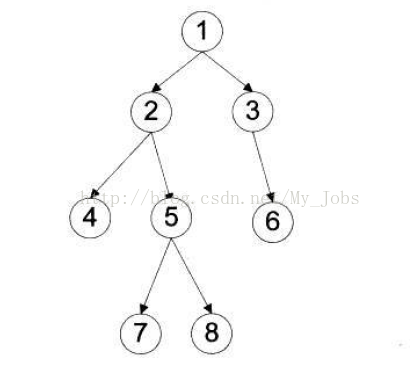
在这里插入图片描述

前序遍历：1 2 4 5 7 8 3 6

中序遍历：4 2 7 5 8 1 3 6

后序遍历：4 7 8 5 2 6 3 1

层次遍历：1 2 3 4 5 6 7 8

3.4.3 postOder

略

调试code

    public static void main(String[] args) {
        BST2<Integer> bst = new BST2<>();
        int[] nums = {5, 3, 6, 8, 4, 2};
        for(int num: nums)
            bst.add(num);

        /
        //      5      //
        //    /   \    //
        //   3    6    //
        //  / \    \   //
        // 2  4     8  //
        /
//        bst.PreOrder();
        System.out.println();
        bst.InOrder();

        System.out.println(bst);


    }
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21

3.4.4 Order 遍历 NR

不用递归的方式实现Tree的遍历

    //TODO Order 不用Recursion的方式，用Stack
    //1 preOrder
    public void PreOrder() throws IllegalAccessException {
        PreOrderNR(root);
    }

    private void PreOrderNR(Node node) throws IllegalAccessException {
        if (node == null) {
            return;
        }
        Stack<Node> Stack = new ArrayStack<>();
        Stack.push(node);

        while (!Stack.isEmpty()){
            Node pop = Stack.pop();
            System.out.println(pop.e);

            if (pop.right != null) {
                Stack.push(pop.right);
            }
            if(pop.left != null){
                Stack.push(pop.left);
            }
        }
        
    }
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26

3.5 Order 遍历广度层序

层序遍历也叫广度遍历
在这里插入图片描述
第一层 0 有的也有叫1
第二层1
…

可以采用Queue的方式实现广度遍历
在这里插入图片描述

    //TODO LevelOrder
    public void levelOrder(){
        if(root == null) return;
        //import java.util.LinkedList;
        //import java.util.Queue;
        Queue<Node> q = new LinkedList<>();
        
        q.add(root);
        while (!q.isEmpty()) {
            Node remove = q.remove();
            System.out.println(remove.e);

            if (remove.left != null) {
                q.add(remove.left);
            } else if (remove.right != null) {
                q.add(remove.right);
            }
        }
    }
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19

3.5.2 广度优先遍历的意义

最快找到问题的解
算法设计-最短路径

在这里插入图片描述

3.6 search max & min

    //TODO 寻找BST中的最小元素
    public E minimun() throws IllegalAccessException {
        if(size == 0)
            throw new IllegalAccessException("BST is empty");
        Node minimum = minimum(root);
        return minimum.e;
    }

    private Node minimum(Node node){
        if (node.left == null) {
            return node;
        }
        return minimum(node.left);
    }


    //TODO max of the BST
    public E maxmum() throws IllegalAccessException {
        if(root == null) throw new IllegalAccessException("BST is empty");

        Node maxmum = maxmum(root);
        return maxmum.e;
    }

    public Node maxmum(Node node){
        if (node.right == null) {
            return node;
        }
        return maxmum(node.right);
    }
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30

3.7 delete max & min

    //TODO delete the max
    public E removeMax() throws IllegalAccessException {
        E maxmum = maxmum();
        root = removeMax(root);

        return maxmum;
    }
    private Node removeMax(Node node){
        if (node.right == null) {
            Node leftNode = node.left;
            node.left = null;
            size--;
            return leftNode;
        }

        node.right = removeMax(node.right);
        return node;
    }



    //TODO delete the min
    public E removeMin() throws IllegalAccessException {
        E minimum = minimun();
        root = removeMin(root);

        return minimum;
    }

    private Node removeMin(Node node){
        if (node.left == null) {
            Node rightNode = node.right;
            node.right = null;
            size--;
            return rightNode;
        }

        node.left = removeMin(node.left);
        return node;
    }
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40

3.8 delete elements

子节点isNull 删除很容易

Hibbard Deletion

左右节点都不为空，
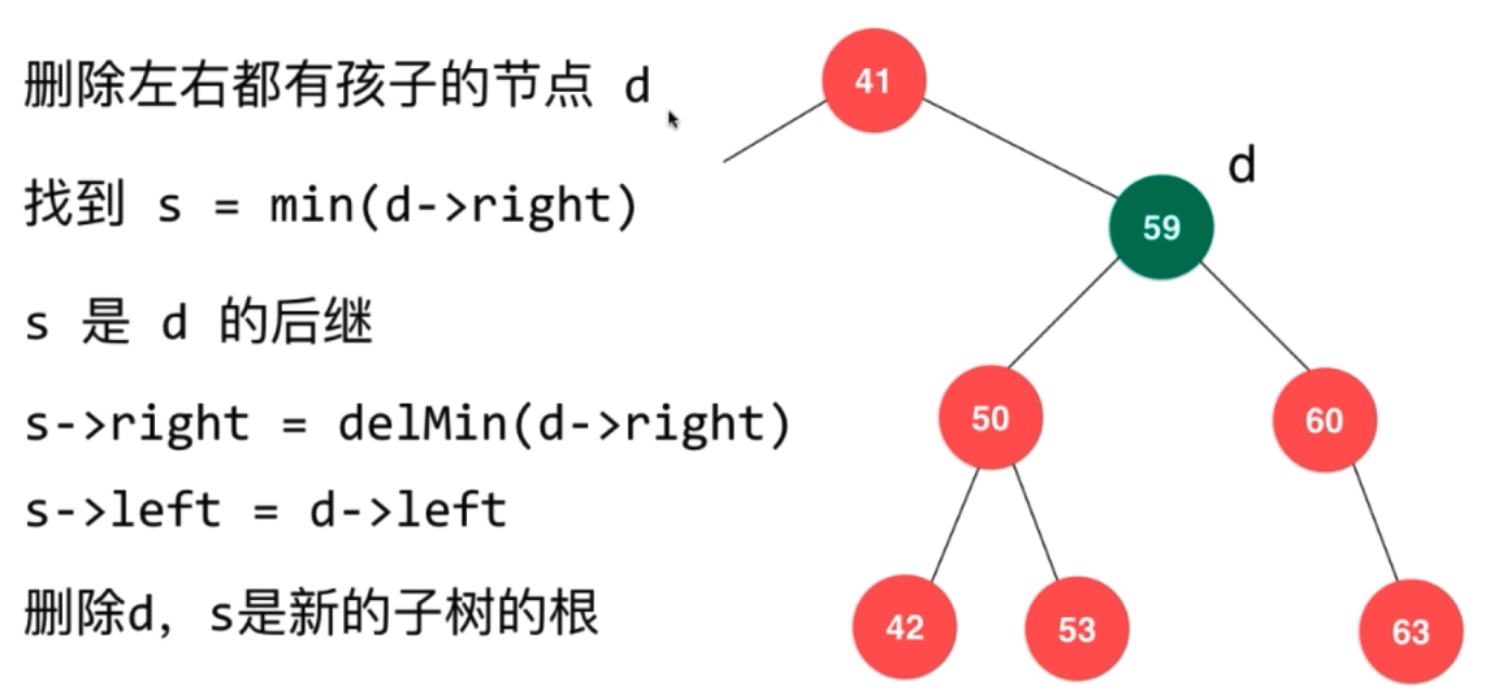
在这里插入图片描述

    //TODO delete the elements
    public void remove(E e){
        root = remove(root,e);
    }

    private Node remove(Node node,E e){
        if(node == null) return null;
        if (e.compareTo(node.e) < 0) {
            node.left = remove(node.left,e);
            return node;
        }
        else if(e.compareTo(node.e) > 0){
            node.right = remove(node.right,e);
            return node;
        }else { // e.compareTo(node.e) == 0

            //带删除节点左子树为空
            if (node.left == null) {
                Node right = node.right;
                node.right = null;
                size--;
                return right;
            }

            //带删除节点右子树为空
            if (node.right == null) {
                Node left = node.left;
                node.left = null;
                size--;
                return left;
            }
            //Hibbard Deletion

            Node successor = minimum(node.right);
            successor.right = removeMin(node.right);//size--
            successor.left = node.left;
            
            node.left = node.right = null;
            
            return successor;
        }
    }

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43

在这里插入图片描述
也可以用d.left 中的最大值来填充一样保持BST

3.9 满二叉树

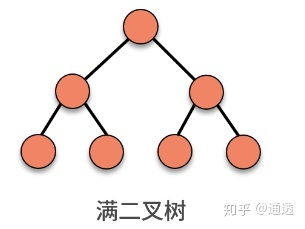
在这里插入图片描述
叶子结点外，所有节点都必须有两个子节点

3.10 完全二叉树

在这里插入图片描述

除最后一层节点外，其他各层节点都必须有两个子节点，且最后一层节点左排列

四. 集合

二分搜索树
不能盛放重复的元素
非常好的实现"集合"的底层数据结构

Set<E>
1

void add(E) ---------------->不能添加重复的元素
void remove(E)
boolean contains(E)
int getSize()
boolean isEmpty()

public class BST<E extends Comparable<E>> {

    private class Node {
        public E e;
        public Node left, right;

        public Node(E e) {
            this.e = e;
            left = null;
            right = null;
        }
    }

    private Node root;
    private int size;

    public BST(){
        root = null;
        size = 0;
    }

    public int size(){
        return size;
    }

    public boolean isEmpty(){
        return size == 0;
    }

    // 向二分搜索树中添加新的元素e
    public void add(E e){

        if(root == null){
            root = new Node(e);
            size ++;
        }
        else
            add(root, e);
    }

    // 向以node为根的二分搜索树中插入元素e，递归算法
    private void add(Node node, E e){
        if(e.equals(node.e))
            return;
        else if(e.compareTo(node.e) < 0 && node.left == null){
            node.left = new Node(e);
            size ++;
            return;
        }
        else if(e.compareTo(node.e) > 0 && node.right == null){
            node.right = new Node(e);
            size ++;
            return;
        }

        if(e.compareTo(node.e) < 0)
            add(node.left, e);
        else //e.compareTo(node.e) > 0
            add(node.right, e);
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61

改进添加操作深入理解递归

向以node为根的二分搜索树中插入元素e，递归算法

//返回插入新节点后二分搜索树的根
    private Node add(Node node, E e){
        if(node == null){
            size ++;
            return new Node(e);
        }

        if(e.compareTo(node.e) < 0)
            node.left = add(node.left, e);
        else if(e.compareTo(node.e) > 0)
            node.right = add(node.right, e);
            
        return node;
1
2
3
4
5
6
7
8
9
10
11
12
13

// 看以node为根的二分搜索树中是否包含元素e, 递归算法

    // 看以node为根的二分搜索树中是否包含元素e, 递归算法
    private boolean contains(Node node, E e){

        if(node == null)
            return false;

        if(e.compareTo(node.e) == 0)
            return true;
        else if(e.compareTo(node.e) < 0)
            return contains(node.left, e);
        else // e.compareTo(node.e) > 0
            return contains(node.right, e);
    }
1
2
3
4
5
6
7
8
9
10
11
12
13

二分搜索树的前序遍历

    // 二分搜索树的前序遍历
    public void preOrder(){
        preOrder(root);
    }

    // 前序遍历以node为根的二分搜索树, 递归算法
    private void preOrder(Node node){
        if(node == null)
            return;

        System.out.println(node.e);
        preOrder(node.left);
        preOrder(node.right);
    }

    @Override
    public String toString(){
        StringBuilder res = new StringBuilder();
        generateBSTString(root, 0, res);
        return res.toString();
    }

    // 生成以node为根节点，深度为depth的描述二叉树的字符串
    private void generateBSTString(Node node, int depth, StringBuilder res){

        if(node == null){
            res.append(generateDepthString(depth) + "null\n");
            return;
        }

        res.append(generateDepthString(depth) + node.e + "\n");
        generateBSTString(node.left, depth + 1, res);
        generateBSTString(node.right, depth + 1, res);
    }

    private String generateDepthString(int depth){
        StringBuilder res = new StringBuilder();
        for(int i = 0 ; i < depth ; i ++)
            res.append("--");
        return res.toString();
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42

声明：本文内容由网友自发贡献，不代表【wpsshop博客】立场，版权归原作者所有，本站不承担相应法律责任。如您发现有侵权的内容，请联系我们。转载请注明出处：https://www.wpsshop.cn/w/Guff_9hys/article/detail/747796

数据结构入门-6-二叉树_二叉树叶子节点

文章目录

一.树结构

1.2 数的性质

二. 二叉树(多叉树)

2.2 二叉树的性质

三. 二分搜索树

3.2 BST add elements

3.3 BST search elements

3.4 Order 遍历 深度

3.4.1 preOder

3.4.2 inOder

3.4.3 postOder

3.4.4 Order 遍历 NR

3.5 Order 遍历 广度 层序

3.5.2 广度优先遍历的意义

3.6 search max & min

3.7 delete max & min

3.8 delete elements

Hibbard Deletion

3.9 满二叉树

3.10 完全二叉树

四. 集合

改进添加操作 深入理解递归

二分搜索树的前序遍历

3.4 Order 遍历深度

3.5 Order 遍历广度层序

改进添加操作深入理解递归