【A*算法——清晰解析 算法逻辑——算法可以应用到哪些题目】例题1.第K短路_a*算法例题

欢迎观看我的博客，如有问题交流，欢迎评论区留言，一定尽快回复！（大家可以去看我的专栏，是所有文章的目录）
　
文章字体风格：
红色文字表示：重难点★✔
蓝色文字表示：思路以及想法★✔
　
如果大家觉得有帮助的话，感谢大家帮忙
点赞！收藏！转发！

A*算法是什么

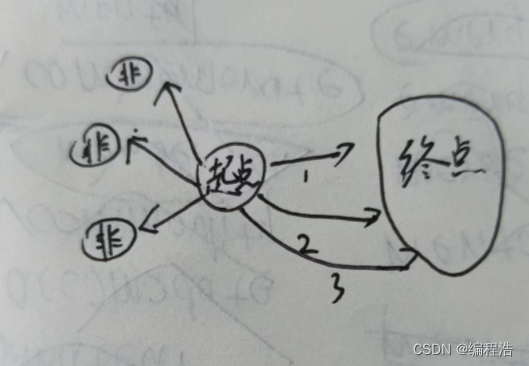
比如如图，我们要搜索从起点到终点的最小距离

起点 一共连接6条边，

我们如果通过 起点的6条边 bfs 搜索 终点

万一搜索的第一挑边是 左上角那条，那么接下来的bfs会优先走这一条，但是这一条如果连接了 特比多边，就会导致，我们的算法时间复杂度非常大

那么我们优化办法就来了，就是

优先走 起点6条边中的 距离终点较 短的 路

怎么实现呢？

我们先从终点往外遍历，记录所有边到终点的距离，那么我们就会知道
起点的6条边中，哪一条边 距离终点较近

优先遍历这条就是了

以上就是A*算法的逻辑
也就是需要 预先处理一下 所有边到终点的最短距离（直接从终点开始遍历）

例题1. 第K短路

原题链接

题意解析

本题求A点到B点
路径长度排名第K 的 路径长度大小 是多少

我们画图自己简单分析一下，可以得出
A点到B点 会有非常非常多的路径走法

那么具体走哪些部分呢？

那就是 先走 距离B较小的路径部分
那么就用到了A*算法思想

我们先预处理一下，B点到所有点的最短距离

然后从A开始走，A点会连接很多点，但是先走 距离A点+距离B点 总和较小的点

如果走到了B那么就不再继续走

但是别的路径还是继续走

直到走到B为K次，那么

此时的路径就是 第K长度

#include <cstring>
#include <iostream>
#include <algorithm>
#include <queue>

#define x first
#define y second

using namespace std;

typedef pair<int, int> PII;
typedef pair<int, PII> PIII;
const int N = 1010, M = 200010;

int n, m, S, T, K;
int h[N], rh[N], e[M], w[M], ne[M], idx;
int dist[N], cnt[N];
bool st[N];

void add(int h[],int a,int b,int c)
{
    e[idx] = b;
    w[idx] = c;
    ne[idx] = h[a];
    h[a] = idx++;
}

void dijkstra()
{
    priority_queue<PII,vector<PII>,greater<PII>> heap;
    heap.push({0,T});//终点
    memset(dist, 0x3f, sizeof dist);
    dist[T] = 0;

    while(heap.size())
    {
        auto t = heap.top();
        heap.pop();

        int ver = t.y;
        if(st[ver]) continue;
        st[ver] = true;

        for(int i=rh[ver];i!=-1;i=ne[i])
        {
            int j = e[i];
            if(dist[j]>dist[ver]+w[i])
            {
                dist[j] = dist[ver] + w[i];
                heap.push({dist[j],j});
            }
        }
    }
}

int astar()
{
    priority_queue<PIII, vector<PIII>, greater<PIII>> heap;
    // 谁的d[u]+f[u]更小 谁先出队列
    heap.push({dist[S], {0, S}});
    while(heap.size())
    {
        auto t = heap.top();
        heap.pop();
        int ver = t.y.y,distance = t.y.x;
        cnt[ver]++;
        //如果终点已经被访问过k次了 则此时的ver就是终点T 返回答案

        if(cnt[T]==K) return distance;

        for(int i=h[ver];i!=-1;i=ne[i])
        {
            int j = e[i];
            /* 
            如果走到一个中间点都cnt[j]>=K，则说明j已经出队k次了，且astar()并没有return distance,
            说明从j出发找不到第k短路(让终点出队k次)，
            即继续让j入队的话依然无解，
            那么就没必要让j继续入队了
            */
            if(cnt[j] < K)
            {
                // 按 真实值+估计值 = d[j]+f[j] = dist[S->t] + w[t->j] + dist[j->T] 堆排
                // 真实值 dist[S->t] = distance+w[i]
                heap.push({distance+w[i]+dist[j],{distance+w[i],j}});
            }
        }
    }
    // 终点没有被访问k次
    return -1;
}

int main()
{
    cin >> m >> n;
    memset(h,-1,sizeof h);
    memset(rh,-1,sizeof rh);
    for(int i=0;i<n;i++)
    {
        int a,b,c;
        cin >> a >> b >> c;
        add(h,a,b,c);
        add(rh,b,a,c);
    }
    cin >> S >> T >> K;
    // 起点==终点时 则d[S→S] = 0 这种情况就要舍去 ,总共第K大变为总共第K+1大 
    if (S == T) K ++ ;
    // 从各点到终点的最短路距离 作为估计函数f[u]
    dijkstra();
    cout << astar();
    return 0;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111