用户特征工程 超详细解读_用户数据特征工程

项目github地址：bitcarmanlee easy-algorithm-interview-and-practice
欢迎大家star，留言，一起学习进步

在网上找到了美团一位叫付晴川同学些的ppt，里面有一幅描述用户特征工程的图，感觉总结得还是比较到位的。现在把图片贴出来：

这张图将用户特征工程里的大面基本都囊括了。因为ppt本身做得比较简单，现在我们试图针对图里的每一项，结合具体的业务场景，做个比较详细的分析。

1.原始数据提取

原作者画图的时候将第一项命名为特征提取，我觉得作者想表达的本意应该是从哪获得相关数据，所以叫原始数据提取可能更为合适一些。

1.业务logs

这部分数据肯定是实际应用场景的大头。只要是个IT公司，每家肯定都有自己的日志或者业务数据。像电商网站的订单数据一般都是存在mysql/oracle/sqlserver等数据库中，用户浏览item/search等行为的数据一般都有相应的日志进行记录。拿到这些数据之后就可以进行后续的分析挖掘动作了。

2.web公开数据抓取

这部分数据就是通过爬虫抓取的数据了，比如最常见的搜索引擎抓取网站内容用于索引的那些搜索引擎爬虫。
看到过一些有趣的数据：2013年来自Incapsula一份互联网报告显示，目前有61.5%的互联网流量不是由人类产生的，如果你读到了这篇文章，你就是那个少数派（人类）。换句话说，实际上互联网流量大部分都是爬虫产生的。。。
正因为现在爬虫已经泛滥成灾，所以很多网站限制爬虫的爬取。所以大家使用爬虫的时候，也尽可能文明使用，做一只文明的爬虫。。。
http://blog.csdn.net/bitcarmanlee/article/details/51824080 这是之前写过的一个简单的爬取糗事百科段子的爬虫，供大家参考。

3.第三方合作

这部分没有太多可说的。当自己数据不够的情况下，可以通过某些渠道与其他公司或者专门的数据公司合作，获得相关数据。例如广告系统中，很多公司都会使用秒针或者Admaster之类的第三方监测机构的数据。

2.数据清洗

拿到原始数据以后，对原始数据进行清洗时非常重要的步骤。因为获得的原始数据里面有非常多的脏数据甚至错误数据，如果不对这些数据进行处理，会极大地影响最后模型的效果。所以数据清洗时非常重要的一个步骤。

1.异常值分析过滤

顾名思义，异常值分析过滤是分析检验数据中是否有错误数据或者不合理的数据。如果有，则将这些数据剔除。常见的异常值分析方法有;

1)简单统计量分析方法
可以对变量做一个描述性的统计与分析，然后查看数据是否合理。例如比较常用的统计量包括最大值与最小值，如果变量超过了最大值最小值的范围，那这个值就为异常值。例如年龄属性，如果某人填写为200或者-1，这显然都是属于异常值的范畴。

2)3$\sigma$原则
如果数据的分布服从高斯分布(正态分布)，3原则是指，测量值如果与平均值的偏差超过$3\sigma$，即为异常值。理论依据如下：
当$X\sim N(0,1)$， p { − 1 ≤ X ≤ 1 } = 0.683 p\{-1 \leq X \leq 1\} = 0.683 p{−1≤X≤1}=0.683， p { − 2 ≤ X ≤ 2 } = 0.954 p\{-2 \leq X \leq 2\} = 0.954 p{−2≤X≤2}=0.954， p { − 3 ≤ X ≤ 3 } = 0.997 p\{-3 \leq X \leq 3\} = 0.997 p{−3≤X≤3}=0.997。那么如果随机变量$X$服从正态分布，从$\mu -3\sigma$到$\mu +3\sigma$的区间内，概率密度曲线下的面积占总面积的99.7%。换句话说，随机变量$X$落在$\mu -3\sigma$到$\mu +3\sigma$的区间外的概率只有0.3%。这就是3$\sigma$原则。

原理很简单，但是非常实际，三个标准差以外的数据就可以认为是异常值了。另外，同学们请对一下三个数字敏感：0.683,0.954,0.997。
这部分内容最后给一张高斯分布的曲线图:

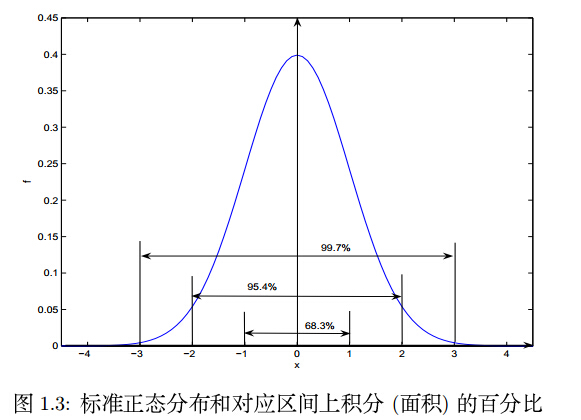
2.数据类型检查

这一个步骤能避免后续出现的很多问题。例如年龄这个属性，应该全是数值类型。但是很多时候这个字段出现了字符串类型的值，很明显这就是异常值，需要进行相应的处理。比如根据身份证号来进行计算，或者给个特殊的值-99来标识等等。

3.清洗换行符制表符空格等特殊字符

如果原始数据某些字段中存在换行符空格制表符等特殊字符，绝大部分情况下会影响后面进一步的分析。所以在数据清洗阶段，根据业务需求处理掉这些特殊字符是很有必要的。例如在大部分场景中，清洗掉字符串中的换行符，都是很必要的。

3.数据预处理

在原图中，作者将这一步命名为值处理，表达的意思应该是一致的。这一步的处理过程非常重要，涉及到的点也比较多，为大家选择一些常见的一一道来。

1.数据平滑

因为现在机器学习的主流是统计机器学习，既然是统计，自然就离不开概率的计算。例如在对文本进行分类时，语料库毕竟是有限的。假设$w_1$,$w_2$,$w_3$没在语料库中出现过，那根据最大似然估计MLE，这些词出现的概率为0。但是实际上这些词出现的概率肯定是不为0的。像最大似然估计里涉及到很多概率的连乘计算，如果一个概率为0，就会导致整体计算结果为0。这时候，就需要我们对数据进行平滑了。
平滑的算法有很多。最简单的平滑方式属于加1平滑了，就是给每种情况出现的次数都加上1，这样就避免了概率为0的情况。这种方式简单粗暴，实际使用的效果一般也不会特别理想。当然还有Good-turning平滑，线性插值平滑（Linear Interpolation Smoothing）等其他算法，根据具体的业务场景进行选择。

2.归一化

归一化也是常见的数据预处理操作。归一化的具体细节请参考http://blog.csdn.net/bitcarmanlee/article/details/51353016一文。

3.离散化

离散化是把连续型的数据分为若干段，是数据分析与数据挖掘中经常采用的一种方法。对数据进行离散化，最大的好处就是有些算法只接受离散型变量。例如决策树，朴素贝叶斯等算法，不能以连续型变量为输入。如果输入时连续型数据，必须要先经过离散化处理。
常见的离散化方式有等距与等频离散化，都比较容易理解。等距就是将连续型随机变量的取值范围均匀划为n等份，每份的间距相等。例如年龄本来是个连续值，用等距离散化以后，1-10，10-20，20-30，30-40等各划为一组。而等频则是把观察点均分为n等份，每份里面包含的样本相同。例如有1万个样本，将样本按采样时间顺序排列，然后按一千个样本为一组，将全部的样本分为十等份。
当然离散化，包括前面的归一化，都是会有负面效果的，这个负面效果就是会带来信息的损失。比如本来我们本来有详尽的年龄数据，在决策树算法或者贝叶斯算法中为了算法的需要，不得已将年龄变为儿童青少年壮年老年这样的离散变量，信息肯定就不如具体的年龄大小那么准确与详尽。所以在使用归一化，离散化等数据处理分析手段时，要结合具体的实际情况，谨慎使用。
http://blog.csdn.net/bitcarmanlee/article/details/51472816一文中专门讲解了one-hot编码，就是数据离散化的一种具体形式。

4.dummy coding

这部分实际中我没怎么使用过，后续找相关资料再进行补充。

5.缺失值填充

数据中某些字段缺失是数据分析挖掘中非常头疼的一个问题。现实世界中的数据往往非常杂乱非常脏，原始数据中某个字段或者某些字段缺失是非常常见的现象。但是尽管数据有缺失，生活还要继续，工作还得继续。面对这种情况，该怎样继续呢？

方法一：丢弃
最简单的方式，如果发现数据有缺失，直接删除这个字段或者将整个样本丢弃。如果大部分样本的某个字段都缺失，那么很明显这个字段就是不可用状态。如果某条样本的大部分字段都缺失，那么很明显这个样本就是不可用状态。这种处理方式简单粗暴，效率高，但是很明显适用范围有限，只适合数据缺失较少的情况。如果某个特征特别重要，数据缺失情况还特别严重，那么美别的办法，老老实实重新采集数据吧。

方法二：统计值填充
如果某个属性缺失，特别是数值类型的属性，可以根据所有样本关于这维属性的统计值填充，常见的有平均值、中值、分位数、众数、随机值等。这种方式难度也不大，效果一般。最大的副作用就是人为带来了不少噪声。

方法三：预测填充
用其他变量做预测模型来预测缺失值，效果一般比统计值填充要好一些。但是此方法有一个根本缺陷，如果其他变量和缺失变量无关，则预测的结果无意义。如果预测结果相当准确，则又说明这个变量是没必要加入建模的。一般情况下，介于两者之间。

方法四：将变量映射到高维空间
比如性别，有男、女、缺失三种情况，则映射成3个变量：是否男、是否女、是否缺失。连续型变量也可以这样处理。比如Google、百度的CTR预估模型，预处理时会把所有变量都这样处理，达到几亿维。这样做的好处是完整保留了原始数据的全部信息、不用考虑缺失值、不用考虑线性不可分之类的问题。缺点是计算量大大提升。而且只有在样本量非常大的时候效果才好，否则会因为过于稀疏，效果很差。(本小结内容来自知乎)

6.分词 tf/idf

严格意义上说，分词属于NLP的范畴。既然原图中提到了分词tf/idf，我们就简单介绍一下。
TF-IDF全称为term frequency–inverse document frequency。TF就是term frequency的缩写，意为词频。IDF则是inverse document frequency的缩写，意为逆文档频率。tf-idf通常用来提取关键词。比如，对一个文章提取关键词作为搜索词，就可以采用TF-IDF算法。
要找出一篇文章中的关键词，通常的思路就是，就是找到出现次数最多的词。如果某个词很重要，它应该在这篇文章中多次出现。于是，我们进行词频TF统计。但是，在中文文献里，的地得了等类似的词汇出现的频率一定是最高的，而且这类词没什么实际的含义，我们就叫他停用词，一般遇到停用词就将他扔掉。
扔掉停用词以后，我们也不能简单地认为出现频率最高的词就是我们所需要的关键字。如果一个词很少见，但是它在某个文章中反复出现多次，那么可以认为这个词反应了这个文章的特性，可以把它作为关键词。在信息检索中，这个权重非常重要，它决定了关键词的重要度，这个权重叫做逆文档频率，它的大小与一个词的常见程度成反比。
在知道了词频和权重之后，两者相乘，就得到一个词的TF-IDF值，某个词对文章的重要性越高，它的TF-IDF值就越大。所以，排在最前面的几个词，就是这篇文章的关键词。
分词有许多开源的工具包可以使用，例如中文分词可以使用结巴分词。

4.特征选择

终于到我们最关键的特征选择部分了。记得我看到过这么一个观点：不论什么算法与模型，效果的上限都是由特征来决定的，而不同的算法与模型只是不断地去逼近这个上限而已。我自己对这个观点也深以为然。特征选择的重要性由此就可见一斑。

特征选择算法可以被视为搜索技术和评价指标的结合。前者提供候选的新特征子集，后者为不同的特征子集打分。 最简单的算法是测试每个特征子集，找到究竟哪个子集的错误率最低。这种算法需要穷举搜索空间，难以算完所有的特征集，只能涵盖很少一部分特征子集。 选择何种评价指标很大程度上影响了算法。而且，通过选择不同的评价指标，可以吧特征选择算法分为三类：包装类(wrapper)、过滤类(filter)和嵌入类(embedded)方法。(本段描述来自wiki百科)

1.embedded 嵌入类方法

嵌入类算法在模型建立的时候，会考虑哪些特征对于模型的贡献最大。最典型的即决策树系列算法，如ID3算法、C4.5算法以及CART等。决策树算法在树生成过程中，每次回选择一个特征。这个特征会将原样本集划分成较小的子集，而选择特征的依据是划分后子节点的纯度，划分后子节点越纯，则说明划分效果越好。由此可见决策树生成的过程也就是特征选择的过程。
另外一个标准的嵌入类方法是正则的方式，例如我们反复提到L1正则的方式可以用来做特征选择。L1正则中，最后系数为0的特征说明对模型贡献很小，我们保留系数不为0的特征即可，这样就达到了特征选择的目的。关于正则的详细内容可以参考：
http://blog.csdn.net/bitcarmanlee/article/details/51932055。

2.wrapper 包装类方法

封装式特征选择是利用学习算法的性能来评价特征子集的优劣。因此，对于一个待评价的特征子集，Wrapper方法需要训练一个分类器，根据分类器的性能对该特征子集进行评价。Wrapper方法中用以评价特征的学习算法是多种多样的，例如决策树、神经网络、贝叶斯分类器、近邻法以及支持向量机等等。
相对于Filter方法，Wrapper方法找到的特征子集分类性能通常更好。但是因为Wrapper方法选出的特征通用性不强，当改变学习算法时，需要针对该学习算法重新进行特征选择；由于每次对子集的评价都要进行分类器的训练和测试，所以算法计算复杂度很高，尤其对于大规模数据集来说，算法的执行时间很长。(比部分内容来自jason的blog)

3.filter 过滤类方法

过滤类方法是实际中使用最广泛最频繁的特征选择方法。过滤特征选择方法运用统计方法将一个统计值分配给每个特征，这些特征按照分数排序，然后决定是被保留还是从数据集中删除。
常见的统计量包括信息增益，信息熵类。详情可参考http://blog.csdn.net/bitcarmanlee/article/details/51488204。
卡方也是常见的用于做特征选择的方式。
另外fisher scores也是filter过滤类中常见的指标。

5.特征组合

严格意义上来说，特征组合也属于特征选择的一部分。取工业界最常见的LR模型为例，LR模型本质上是广义线性模型(对数线性模型)，实现简单而且容易并行，计算速度也比较快，同时使用的特征比较好解释，预测输出的概率在0与1之间也非常方便易用。但是，与一般模型的容易overfitting不一样，LR模型却是一个underfitting模型，因为LR模型本身不够复杂，甚至可以说相当简单。而现实中很多问题不仅仅是线性关系，更多是复杂的非线性关系。这个时候，我们就希望通过特征组合的方式，来描述这种更为复杂的非线性关系。

目前常见的用于特征组合的方法：

1.GBDT

2014年facebook发表了一篇paper，讲的就是GBDT+LR用于特征组合，发表以后引起比较大的反响。文章名为Practical Lessons from Predicting Clicks on Ads at Facebook，有兴趣的同学们可以google一把。

2.FM

FM算法也是用于对特征进行组合的一种方式。FM算法的具体细节，可以参考http://blog.csdn.net/bitcarmanlee/article/details/52143909。

6.数据降维

降维，又被称为维度规约。现实世界中得到的数据一般都有冗余，要么有一些是无用信息，要么有一些是重复的信息，我们针对这部分冗余数据进行一些处理之后，可以明显减少数据的大小与维度的多少。给大家举个很简单的实际场景，用iphone拍出来的原始照片一般大小都为2-3M。但是我们通过qq或者微信等工具传输这些照片的时候，发现传输成功以后这些照片的大小就变成只有几十KB了，这就是因为在传输照片的过程中，事先会对照片进行压缩，压缩完毕以后再进行传送以节省宝贵的带宽资源。而这个数据压缩的过程，其实就等同于降维的过程。

很明显数据经过降维处理以后，会大大节约数据存储空间。同时，也会大大较少数据的后续处理计算时间。因此，数据降维技术或者说数据压缩技术，在实际中有非常广泛的应用。

一般来说，数据降维可以从两个方面来实施。比较简单的一种方式是提取特征子集，然后用这部分子集来表示原有数据。例如图像处理里面，如果一幅128128的图片，只有中心3232的部分有非0值，那么就只取中心32*32的部分。另外一种是通过线性/非线性的方式将原来高维空间变换到一个新的空间，这个新的空间维度比原来的高维空间要小，这样就达到了降维的目的。一般大家讨论的所谓降维技术，都是后面一种。

1.主成分分析 Principal Component Analysis(PCA)

PCA是最常用的线性降维方法。PCA的理论认为，特征的主方向，是特征幅度变化最大的方向，既改维度上数据的方差最大。这样经过PCA以后，就可以使用较小的数据维度，保留住较多的原数据点的特性，从而达到降维的目的。
PCA的具体过程，以后会写相关的文章专门介绍。

2.奇异值分解 Singular Value Decomposition(SVD)

SVD也是实际中使用非常广泛的一种方法。关于SVD的详细介绍，请参考http://blog.csdn.net/bitcarmanlee/article/details/52068118。

3.线性判别分析 Linear Discriminant Analysis(LDA)

以上内容，基本就涵盖了用户特征工程的各个大的方面。当然某个实际项目中，不可能上面的所有方法都用到。还是得结合数据的具体情况与业务需求，选择最适合自己的方法！