- 1基于单片机的太阳能热水器控制系统设计_太阳能3d阳台机控制系统界面
- 2【DevOps】4大API网关压力性能测试
- 3UOS统信服务器1050-ufu(A/E)免费授权版本仓库切换_镜像的ufu是什么版本
- 4mac redis启动,redis哨兵模式,redis集群的相关命令
- 5“下个月AI觉醒,杀死奥特曼...”好莱坞上线首部AI制作的电影,长达90分钟,取材终结者2_our t2 remake
- 6Visual Studio2022更新,Windows7和32位系统无缘体验_visualstudio支持32电脑的版本
- 7[HttpRunner]简单入门+解决接口依赖&调用环境变量_httprunner依赖结果
- 8C# The process cannot access the file because it is being used by another process
- 9开源模型应用落地-工具使用篇-Spring AI-Function Call(八)
- 10c语言:关于逻辑运算符(逻辑与、逻辑或和逻辑非)不易混淆的记忆方法_c语言逻辑与
ST 2.0 霍尔FOC 的相关难点总结_hall_init_electrical_angle
赞
踩
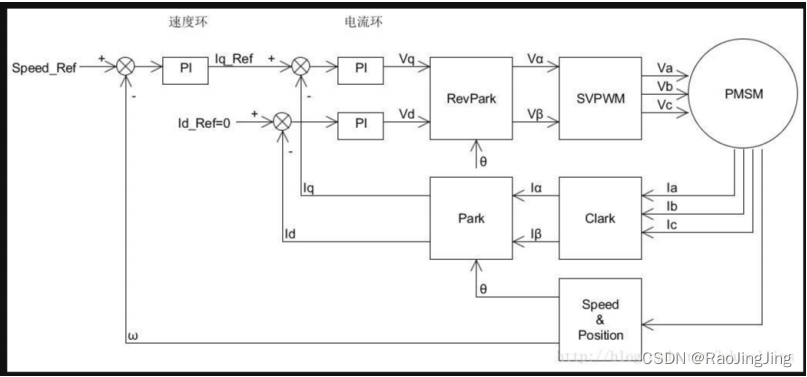
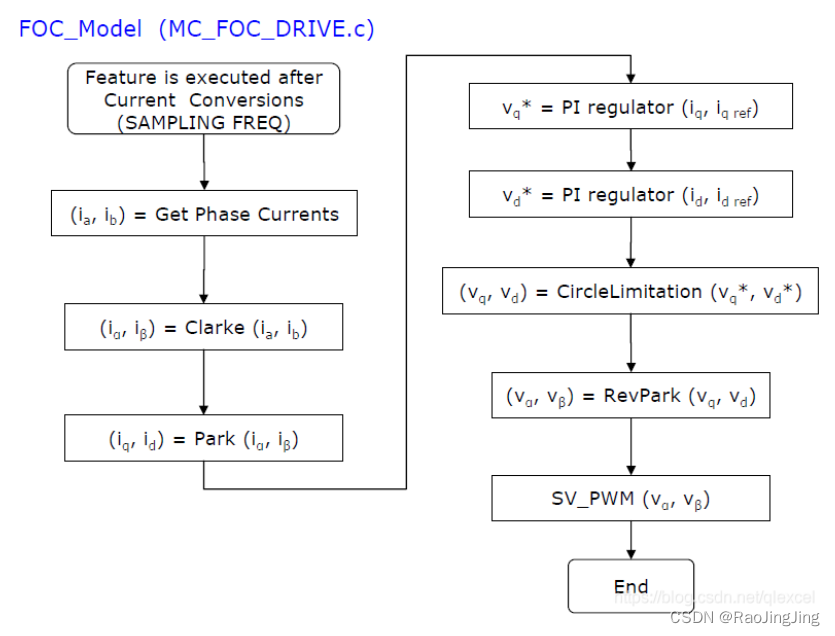
HALL_Init_Electrical_Angle()
-
关于电角度的理解,我的另外一篇博文有介绍。自己去看
-
XOR 波形输出
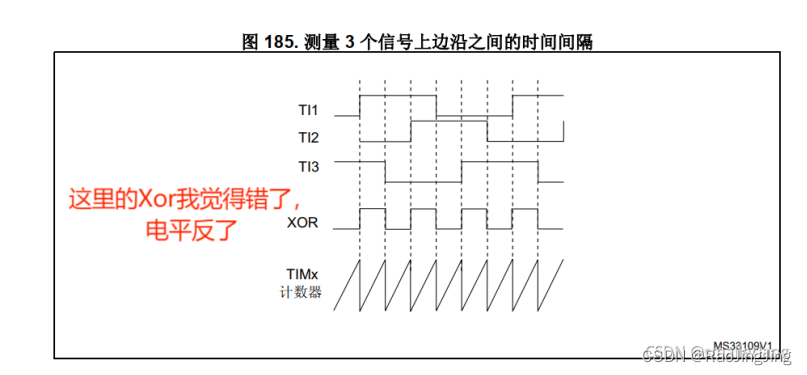
-
hall sensor 的输出状态。
- 由下图可知道不同电平,转子在不同的扇区,以
s
t
a
t
e
X
=
H
3
<
<
2
∣
H
2
<
<
1
∣
H
1
stateX=H3<<2|H2<<1|H1
stateX=H3<<2∣H2<<1∣H1 为例,在图中,state 5在第一扇区,下图是逆时针旋转,
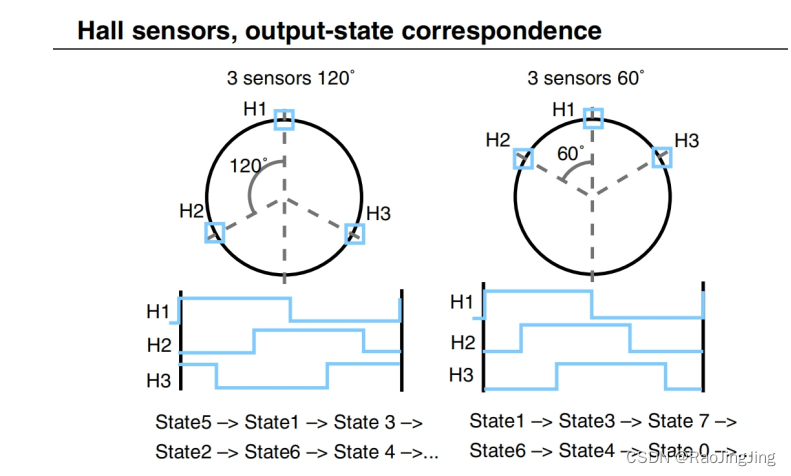
- 由下图可知道不同电平,转子在不同的扇区,以
s
t
a
t
e
X
=
H
3
<
<
2
∣
H
2
<
<
1
∣
H
1
stateX=H3<<2|H2<<1|H1
stateX=H3<<2∣H2<<1∣H1 为例,在图中,state 5在第一扇区,下图是逆时针旋转,
-
将65536 分成306度。取代浮点。那么 65535 360 代表 1 ° \frac{65535}{360}代表 1\degree 36065535代表1°
-
void TIM3_IRQHandler(void)
代码解析-
switch(bHallState),这里只有5,3,6.为什么? 因为stm32F1系列只有单边沿计数捕获。所以只有三种状态。根据xor信号可以看出,在触发下降沿的时候,H3<<2|H2<<1|H1 = 5 ,3, 6
-
正反转,代码和上图结合看,是逆时针是正方形
-
case 5: if(bSpeed<0) { //在下一行基础上加60度,因为每个扇区正好是60度。下面都是这样的 hElectrical_Angle = (s16)(S16_PHASE_SHIFT+S16_60_PHASE_SHIFT); } else if(bSpeed!= ERROR) { hElectrical_Angle = S16_PHASE_SHIFT; }- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
这里电角度我的理解是,假如正转(逆时针)。那么case:5的时候,是第一次到达0,也就是上图中的水平x方向,也就是电角度的0度, 反方向的时候,是顺时针过来的,到case:5的时候,角度是60度。在加上S16_PHASE_SHIFT(这个是A相的最大饭店董事和H1上升沿的角度延迟)。如下图
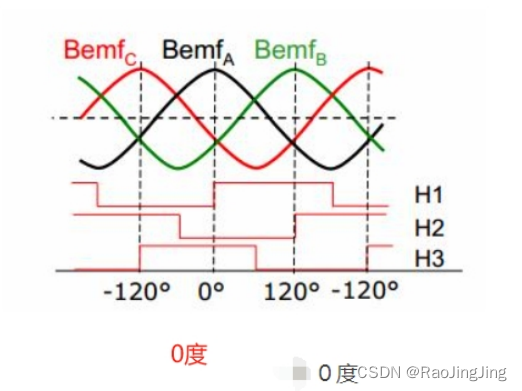
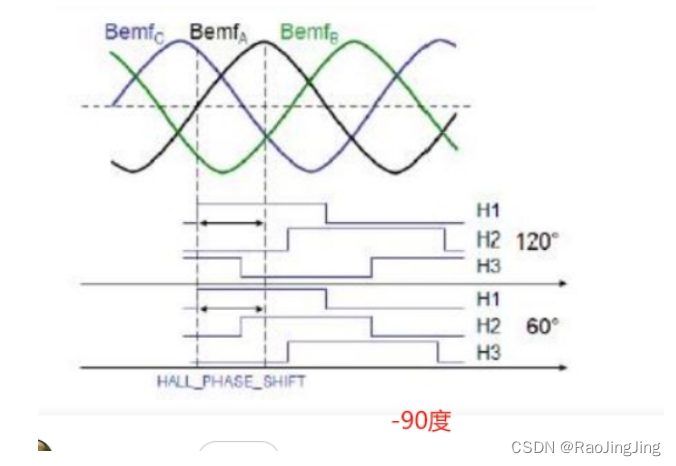
-
同理
case 3: if(bSpeed<0) { //在下一行基础上加60度,因为每个扇区正好是60度。下面都是这样的 hElectrical_Angle = (s16)(S16_PHASE_SHIFT+S16_120_PHASE_SHIFT+ S16_60_PHASE_SHIFT); } else if(bSpeed!= ERROR) { hElectrical_Angle =(s16)(S16_PHASE_SHIFT + S16_120_PHASE_SHIFT); }- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
在case=3的时候,正方向的时候(逆时针)到120度的时候,正好满足刚好到3. 同理负方向(顺时针)需要再加60度,正好一个扇区。
-
s16 HALL_GetRotorFreq ( void )
+PeriodMeasAux = GetAvrgHallPeriod(); hRotorFreq_dpp = (s16)((u16) (PSEUDO_FREQ_CONV / PeriodMeasAux.wPeriod)); hRotorFreq_dpp *= PeriodMeasAux.bDirection;- 1
- 2
- 3
- 4
- 5
P S E U D O _ F R E Q _ C O N V = ( C K T I M ∗ 10 ) / 3 S A M P L I N G _ F R E Q ∗ 10 ⋅ 2 16 PSEUDO\_FREQ\_CONV=\frac{(CKTIM*10) / 3}{SAMPLING\_FREQ * 10}\cdot 2^{16} PSEUDO_FREQ_CONV=SAMPLING_FREQ∗10(CKTIM∗10)/3⋅216
理解hRotorFreq_dpp:
C K T I M w P e r i o s \frac{CKTIM}{wPerios} wPeriosCKTIM也就是得出捕获输入的频率
C K T I M w P e r i o s ⋅ S A M P L I N G _ F R E Q \frac{CKTIM}{wPerios\cdot SAMPLING\_FREQ } wPerios⋅SAMPLING_FREQCKTIM也就是得PWM周期的频率
C K T I M 3 ⋅ w P e r i o s ⋅ S A M P L I N G _ F R E Q \frac{CKTIM}{3\cdot wPerios\cdot SAMPLING\_FREQ } 3⋅wPerios⋅SAMPLING_FREQCKTIM除以3也就是得PWM周期的状态频率,因为只有下降沿触发,所有只有3个状态,3个状态对应着一圈也就是 2 π 2\pi 2π
最后乘以 2 16 2^{16} 216也就是将电角度转化为65535大小。也就是每 2 π 2\pi 2π是65535大小
-
Clark 变换
-
Curr_Components Clarke(Curr_Components Curr_Input)
-
坐标系(这里和匠心科技的手册不一样,手册是 I β I_\beta Iβ向上的):
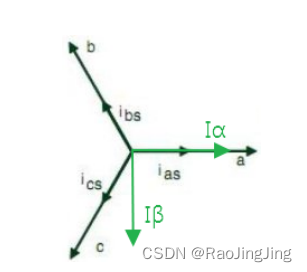
I
α
=
k
(
I
a
−
c
o
s
(
60
)
∗
I
b
−
c
o
s
(
60
)
∗
I
c
)
I_\alpha = k(I_a-cos(60)*I_b-cos(60)*I_c)
Iα=k(Ia−cos(60)∗Ib−cos(60)∗Ic)
I
β
=
k
(
c
o
s
(
30
)
∗
I
c
−
c
o
s
(
30
)
∗
I
b
)
I_\beta = k(cos(30)*I_c-cos(30)*I_b)
Iβ=k(cos(30)∗Ic−cos(30)∗Ib)
I
a
+
I
b
+
I
c
=
0
I_a+I_b+I_c = 0
Ia+Ib+Ic=0
结合上面3个公式可得:
I
α
=
I
a
I
β
=
−
I
a
+
2
∗
I
b
3
I_\alpha = I_a \qquad I_\beta = -\frac{I_a+2*I_b}{\sqrt{3}}
Iα=IaIβ=−3
Ia+2∗Ib
- 数据格式:
- 这里用的都是Q15格式的。也就是1位是符号位,15位是小数位。Q15转浮点除以2^15 = 327678. 浮点转Q15 乘以32768
- 两个Q15 相乘后,等于浮点数*2^30 次,所以要转化为Q15还需要再除以2^15=32768 才能转换为Q15 格式。
- 为什么一开始qIa_divSQRT3_tmp 要除以sqrt(3),这是因为最后求得时候还要除,这里是简化了。
获取电流
- Curr_Components SVPWM_3ShuntGetPhaseCurrentValues(void)
- ADC1->JDR1 << 1 原因:我们是注入组左对齐,因此右移3位才是真实的转换值。电流采样值的Q15格式为:((ADC1->JDR1<<1)>>4)/4096Vref2^15=((((ADC1->JDR1<<1)>>4)>>12)*Vref)<<15=ADC1->JDR1<<1. 因为左对齐中,数据有效位为bit3-bit14,共12位。Vref=2(假设的,不影响)hPhaseAOffset 为Q15格式的零点电流。
- 个人认为代码中wAux = (s32)(hPhaseAOffset)- ((ADC1->JDR1)<<1);是有问题的,应该反过来才对,再st foc 5.3中就是反过来的,所以这里的电流是负值。
park 变换 , 逆park变换
-
Curr_Components Park(Curr_Components Curr_Input, s16 Theta)
-
坐标系(这里和匠心科技的手册不一样,手册是 I β I_\beta Iβ向上的):
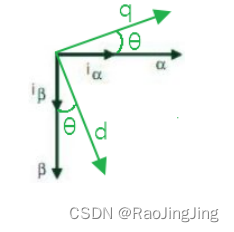
park transform
I q = I α ∗ c o s ( θ ) − I β ∗ s i n ( θ ) I_q = I_\alpha*cos(\theta)-I_\beta*sin(\theta) Iq=Iα∗cos(θ)−Iβ∗sin(θ)
I d = I α ∗ s i n ( θ ) + I β ∗ c o s ( θ ) I_d = I_\alpha*sin(\theta)+I_\beta*cos(\theta) Id=Iα∗sin(θ)+Iβ∗cos(θ)
rev park transform ,逆park变换用于电压。
V α = V q ∗ c o s ( θ ) + V d ∗ s i n ( θ ) V_\alpha = V_q*cos(\theta)+V_d*sin(\theta) Vα=Vq∗cos(θ)+Vd∗sin(θ)
V β = − V q ∗ s i n ( θ ) + V d ∗ c o s ( θ ) V_\beta = -V_q*sin(\theta)+V_d*cos(\theta) Vβ=−Vq∗sin(θ)+Vd∗cos(θ)
逆park变换的幅度限制
-
void RevPark_Circle_Limitation(void)
-
-
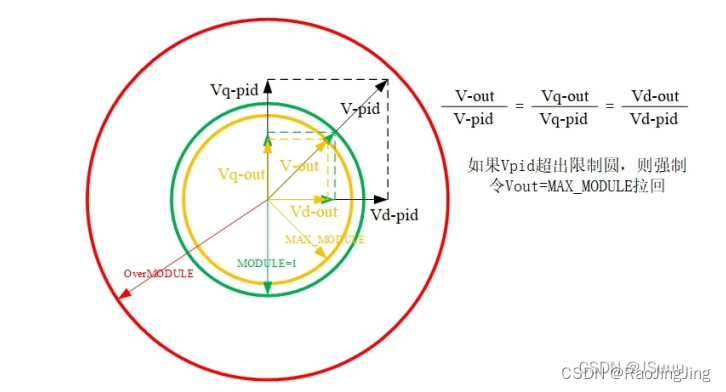
上图可知,当PID的输出V_q,V_d 的模大于极限的时候,需要等比例缩放。
PID 输出为 V q − p i d V d − p i d V_{q-pid} \quad V_{d-pid} Vq−pidVd−pid ,经过限制后的输出为 V q − o u t V d − o u t V_{q-out} \quad V_{d-out} Vq−outVd−out
必定有:
MAXMODULEM = 32768 * 调制比
V q − p i d V q − o u t = V q − p i d 2 + V d − p i d 2 M A X M O D U L E M 2 \frac{V_{q-pid}}{V_{q-out}}=\sqrt{\frac{V_{q-pid}^2+V_{d-pid}^2}{MAXMODULEM^2}} Vq−outVq−pid=MAXMODULEM2Vq−pid2+Vd−pid2
V d − p i d V d − o u t = V q − p i d 2 + V d − p i d 2 M A X M O D U L E M 2 \frac{V_{d-pid}}{V_{d-out}}=\sqrt{\frac{V_{q-pid}^2+V_{d-pid}^2}{MAXMODULEM^2}} Vd−outVd−pid=MAXMODULEM2Vq−pid2+Vd−pid2
st这里就是查表求右边的倒数,记为S_cof.
个人猜测ST源代码里提供了一种巧妙的思路,先假定ST的单位矢量圆半径是32768,即当Vq,Vd的合成矢量满足满调制比时,合成矢量的大小为32768,由此可得出从PID环节输出来的Vq_pid和Vd_pid能够合成的电压矢量范围为0— V q − p i d 2 + V d − p i d 2 = 2 ∗ 3276 8 2 \sqrt{V_{q-pid}^2 + V_{d-pid}^2 }=\sqrt{2*32768^2} Vq−pid2+Vd−pid2 =2∗327682 ,注意,这个范围远远超出了电压调制范围,因此需要在内部加一个限制,以此为基础有:
-
将0—$ {2*32768^2} $ 划分成128等分;
-
设定最大调制比为0.98,则得出满足调制的最大电压矢量MAX_MODULE(约为32111),当Vq_pid和Vd_pid 达到可以合成的最大电压矢量时,即满足 V q − p i d 2 + V d − p i d 2 = M A X M O D U L E M 2 {V_{q-pid}^2 + V_{d-pid}^2 }=MAXMODULEM^2 Vq−pid2+Vd−pid2=MAXMODULEM2 ,此时在128等分中为第61个,即这128等分的前61个电压矢量是可以被利用的。(61是怎么来的?32111^2 正好在0-2*32768^2 划分的128个位置的第61个位置)
-
因为只有当合成矢量大于限制圆时,才需要限制,即处于128等分的后67等分里才需要处理,所以只需要对后67个等分对应的S_cof列表即可。
-
ST代码中先计算PID环节出来后电压矢量所处的等分点区间,然后减去限制圆内的等分点个数,得到在67个等分点范围内的节点号,再去查表得到S_cof,然后重新计算 V q − p i d V d − p i d {V_{q-pid}\quad V_{d-pid}} Vq−pidVd−pid
void RevPark_Circle_Limitation(void) { s32 temp; //计算Vd^2+Vq^2 temp = Stat_Volt_q_d.qV_Component1 * Stat_Volt_q_d.qV_Component1 + Stat_Volt_q_d.qV_Component2 * Stat_Volt_q_d.qV_Component2; // min value 0, max value 2*32767*32767 if ( temp > (u32)(( MAX_MODULE * MAX_MODULE) ) ) // 如果(Vd^2+Vq^2)大于MAX_MODULE^2,就要进行比例缩小 { u16 index; //假设Vq=x*32767, Vd=y*32767 //理解在同目录.md文件里 temp /= (u32)(512*32768); // min value START_INDEX, max value 127,缩小64倍 temp -= START_INDEX ; // min value 0, max value 127 - START_INDEX index = circle_limit_table[(u8)temp]; temp = (s16)Stat_Volt_q_d.qV_Component1 * (u16)(index); //使用缩小系数来缩小Vq Stat_Volt_q_d.qV_Component1 = (s16)(temp/32768); temp = (s16)Stat_Volt_q_d.qV_Component2 * (u16)(index); Stat_Volt_q_d.qV_Component2 = (s16)(temp/32768); } }
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
-
temp /= (u32)(512*32768);- 1
-
temp -= START_INDEX ; // min value 0, max value 127 - START_INDEX- 1
扇区计算 https://www.zhihu.com/people/Temo/posts
-
void SVPWM_3ShuntCalcDutyCycles (Volt_Components Stat_Volt_Input)
-
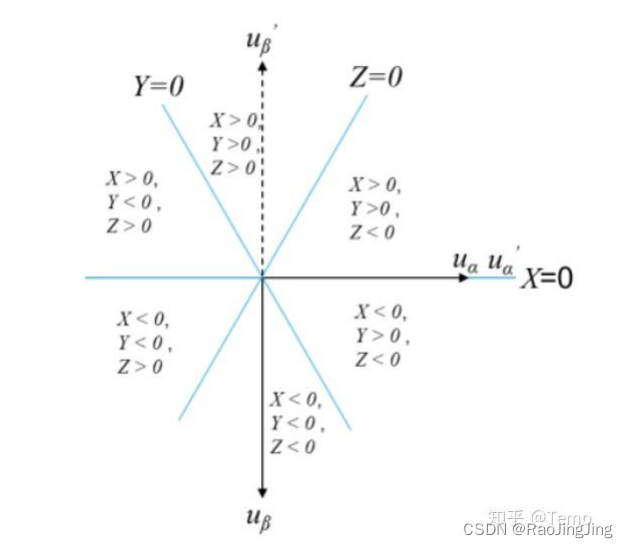
坐标系参考, U β U_\beta Uβ 朝下
-
代码分析
void SVPWM_3ShuntCalcDutyCycles (Volt_Components Stat_Volt_Input) { s32 wX, wY, wZ, wUAlpha, wUBeta; u16 hTimePhA=0, hTimePhB=0, hTimePhC=0, hTimePhD=0; u16 hDeltaDuty; wUAlpha = Stat_Volt_Input.qV_Component1 * T_SQRT3 ; wUBeta = -(Stat_Volt_Input.qV_Component2 * T); wX = wUBeta; wY = (wUBeta + wUAlpha)/2; wZ = (wUBeta - wUAlpha)/2; // Sector calculation from wX, wY, wZ if (wY<0) { if (wZ<0) { bSector = SECTOR_5; } else // wZ >= 0 if (wX<=0) { bSector = SECTOR_4; } else // wX > 0 { bSector = SECTOR_3; } } else // wY > 0 { if (wZ>=0) { bSector = SECTOR_2; } else // wZ < 0 if (wX<=0) { bSector = SECTOR_6; } else // wX > 0 { bSector = SECTOR_1; } } }
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
- 43
- 44
- 45
- 46
- 47
- 48
- 解读: 在以上代码中,可以得到
w X = − U β wX = -U_\beta \quad wX=−Uβ
w Y = − U β + 3 U α 2 wY=\frac{-U_\beta+\sqrt{3}U_\alpha}{2} wY=2−Uβ+3 Uα
w Z = − U β + 3 U α 2 wZ = \frac{-U_\beta+\sqrt{3}U_\alpha}{2} wZ=2−Uβ+3 Uα
然后令 w X = 0 w Y = 0 w Z = 0 wX=0 \quad wY = 0 \quad wZ=0 wX=0wY=0wZ=0 则得到三条直线如上图所示。然后根据如图所示的比较关系判断扇区。扇区从第一象限逆时针开始。
每个相位的执行时间计算 (如果自己记录的不够清楚,可以打开同目录。资源文件目录下的:svpwm_知乎文章_详细.pdf)
-
假设在第一象限
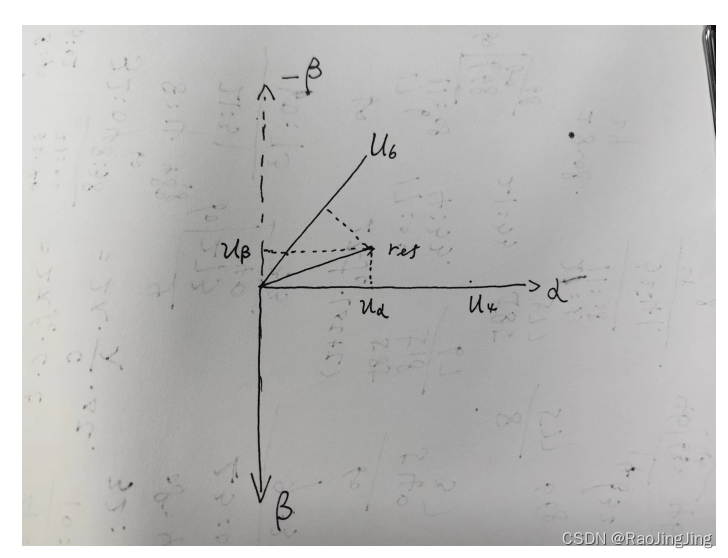
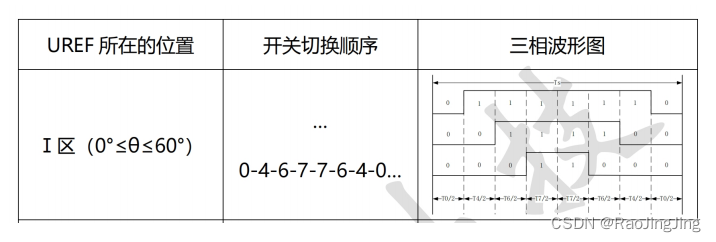
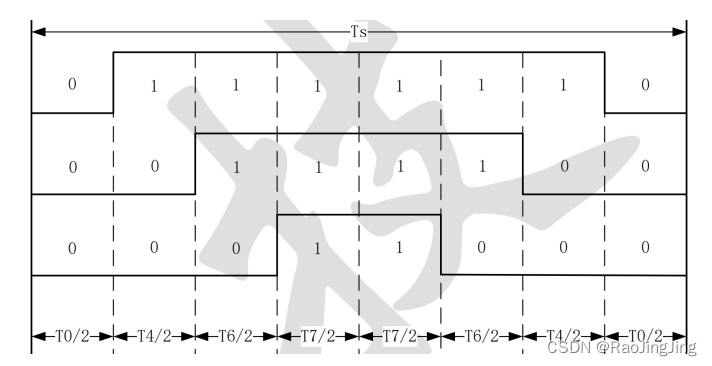
如上图所示:
U 6 = U 4 = 2 ⋅ U d c 3 . . . . ( 1 ) U_6=U_4 = \frac{2\cdot U_{dc}}{3} ....(1) U6=U4=32⋅Udc....(1)
U α ⋅ T s = U 4 ⋅ T 4 + U 6 ⋅ c o s ( 60 ) ⋅ T 6 . . . . ( 2 ) U_{\alpha}\cdot T_s = U_4\cdot T_4 + U_6 \cdot cos(60)\cdot T_6 ....(2) Uα⋅Ts=U4⋅T4+U6⋅cos(60)⋅T6....(2)
− U β ⋅ T s = U 6 ⋅ s i n ( 60 ) ⋅ T 6.. ( 3 ) -U_{\beta}\cdot T_s = U_6 \cdot sin(60)\cdot T6..(3) −Uβ⋅Ts=U6⋅sin(60)⋅T6..(3)
这里有负号的原因是 β 轴是向下的,所以 U β 是负数,这里需要转正 这里有负号的原因是\beta轴是向下的,所以U_\beta是负数,这里需要转正 这里有负号的原因是β轴是向下的,所以Uβ是负数,这里需要转正
(1)(2)(3)可得,同时(2)(3)同时除以 3 U d c \frac{\sqrt{3}}{U_{dc}} Udc3 .:
T 4 = T s ( 3 U α + U β 2 ) T_4={T_s}(\frac{\sqrt{3}U_\alpha + U_\beta}{2}) T4=Ts(23 Uα+Uβ)T 6 = T s ( − U β ) T_6=T_s(-U_\beta) T6=Ts(−Uβ)
∵ w X = − T ⋅ U β w Y = − T ⋅ U β + 3 ⋅ T ⋅ U α 2 w Z = − T ⋅ U β − 3 ⋅ T ⋅ U α 2 \because wX=-T\cdot U_\beta \quad wY=\frac{-T\cdot U_\beta+\sqrt{3}\cdot T \cdot U_\alpha}{2} \quad wZ=\frac{-T\cdot U_\beta-\sqrt{3}\cdot T \cdot U_\alpha}{2} ∵wX=−T⋅UβwY=2−T⋅Uβ+3 ⋅T⋅UαwZ=2−T⋅Uβ−3 ⋅T⋅Uα
and T s = 2 ⋅ T T_s=2\cdot T Ts=2⋅T
因为计数器是上下计数的,所以代码中的T只有周期一半
∴ \therefore ∴
T 4 = 2 T ( 3 U α + U β 2 ) T_4={2T}(\frac{\sqrt{3}U_\alpha + U_\beta}{2}) T4=2T(23 Uα+Uβ)
T 6 = 2 T ( − U β ) T_6=2T(-U_\beta) T6=2T(−Uβ)
∴ T 0 2 = T s − T 4 − T 6 4 = T − T 4 − T 6 2 = T − T ( 3 U α + U β 2 ) + T ⋅ U β 2 = T + T U β − 3 U α 2 2 \therefore \frac{T_0}{2}=\frac{T_s-T_4-T_6}{4}=\frac{T-T_4-T_6}{2}=\frac{T-T(\frac{\sqrt{3}U_\alpha + U_\beta}{2})+T\cdot U_\beta}{2}=\frac{T+T\frac{U_\beta-\sqrt{3}U_\alpha}{2}}{2} ∴2T0=4Ts−T4−T6=2T−T4−T6=2T−T(23 Uα+Uβ)+T⋅Uβ=2T+T2Uβ−3 Uα
以上算的是实际的时间,但是ST里面求得是寄存器比较值。也就是某一相的时间,也即hTimePhA。
∵ T = T s 2 \because T=\frac{T_s}{2} ∵T=2Ts
h T i m e P h A = T − T 0 2 = T − ( T − T 4 − T 6 2 ) = T + T 4 + T 6 2 = T + T ( 3 U α + U β 2 ) − T ⋅ U β 2 = T + T ( 3 U α − U β 2 ) 2 = T + w X − w Z 2 hTimePhA = T-\frac{T_0}{2}=T-(\frac{T-T_4-T_6}{2})=\frac{T+T_4+T_6}{2}=\frac{T+T(\frac{\sqrt{3}U_\alpha + U_\beta}{2})-T\cdot U_\beta}{2}=\frac{T+T(\frac{\sqrt{3}U_\alpha-U_\beta}{2})}{2}=\frac{T+wX-wZ}{2} hTimePhA=T−2T0=T−(2T−T4−T6)=2T+T4+T6=2T+T(23 Uα+Uβ)−T⋅Uβ=2T+T(23 Uα−Uβ)=2T+wX−wZh T i m e P h B = T − T 0 2 − T 4 2 = h T i m e P h A − T 4 2 = h T i m e P h A − T 3 U α + U β 2 = h T i m e P h A − ( − w Z ) = h T i m e P h A + w Z hTimePhB = T-\frac{T_0}{2} -\frac{T_4}{2}=hTimePhA -\frac{T_4}{2}=hTimePhA-T\frac{\sqrt{3}U_\alpha+U_\beta}{2}=hTimePhA-(-wZ) = hTimePhA+wZ hTimePhB=T−2T0−2T4=hTimePhA−2T4=hTimePhA−T23 Uα+Uβ=hTimePhA−(−wZ)=hTimePhA+wZ
h T i m e P h C = T − T 0 2 − T 4 2 − T 6 2 = h T i m e P h B − T 6 2 = h T i m e P h B − T ( − U β ) = h T i m e P h B − w X hTimePhC = T-\frac{T_0}{2} -\frac{T_4}{2}-\frac{T_6}{2}=hTimePhB-\frac{T_6}{2}=hTimePhB-T(-U_\beta)=hTimePhB-wX hTimePhC=T−2T0−2T4−2T6=hTimePhB−2T6=hTimePhB−T(−Uβ)=hTimePhB−wX
注解: 这里的因为计数器是上下计数的,所以代码中的T是实际上是 T s 2 \frac{T_s}{2} 2Ts . 注意上面的额式子中(2)(3)中已经都除以 3 U d c \frac{\sqrt{3}}{U_{dc}} Udc3
-
假设在第一扇区,那么算出来的hTimePhA,hTimePhB,hTimePhC都是运行时间,怎么和PWM匹配的?
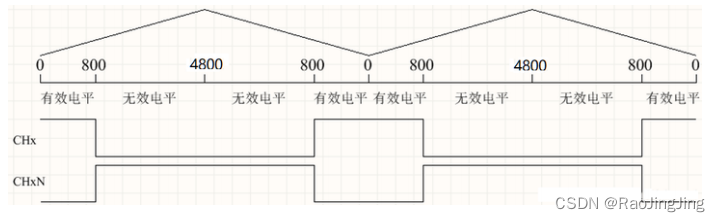
如图所示,三个时间控制的是有效电平。那么是在下三角区域有效的。这个地方很容易搞错。
比如上图的,周期是 perios(ARR)=4800. ,CH1的hTimePhA(CCR1)=800.采用PWM1模式,即CNT < ARR 的时候s输入有效电平。也即高电平,大于的时候输出无效电平。 -
为什么要除以131072。 131072 = 2^15*4. 因为代码中的T= 4*pwm_perios. 那么在扇区一中的计算代码为 h T i m e P h A = T 8 + T + w X − W z 2 2 15 ∗ 4 = p w m _ p e r i o s 2 + p w m _ p e r i o s w X − w Z 2 + T 2 ∗ 2 15 ∗ 4 hTimePhA=\frac{T}{8}+\frac{\frac{T+wX-Wz}{2}}{2^{15}*4}=\frac{pwm\_perios}{2}+pwm\_perios\frac{wX-wZ}{2}+\frac{T}{2*2^{15}*4} hTimePhA=8T+215∗42T+wX−Wz=2pwm_perios+pwm_perios2wX−wZ+2∗215∗4T 尾巴项和推导对不上,但是尾巴项的取值范围不到1.可以忽略不计,感觉是故弄玄虚。



