excel统计分析——两因素有重复方差分析_双因素有重复方差分析excel操作

参考资料：生物统计学

        无重复观测值的两因素方差分析只能研究两个因素的主效应，不能考察因素间的交互作用，只有在确定因素间不存在交互作用时才能进行无重复观测值的试验和分析。为了准确估计因素的主效应、交互作用和随机误差，每个水平组合都应设置重复。

        设A、B两因素分别有a、b个水平，共有ab个水平组合，每个水平组合有n次重复，则共有abn个观测值。线性模型可以表示为：

其中，i=1,2,...,a；j=1,2,...,b；k=1,2,...,n；μ为总平均数；为的效应；为的效应；为与的互作效应；为随机误差，相互独立且都服从。

         若、、分别为、、对应的平均数，则：

且

1、平方和分解

        与无重复观测值的两因素数据相比，有重复观测值的两因素数据的平方和与自由度的分解多出两个因素的互作效应项，即。

 

所以：

2、自由度分解

3、计算均方值

各项的均方为平方和与相应的自由度的比值，这里不再展示。

4、F统计量计算

在计算F统计量之前，需要解释下固定效应和随机效应。

如果因素是认为可控的，如温度、时间、浓度等，称为固定因素，其效应为固定效应。

如果因素是不可控的，如土壤、气候等，称为随机因素，产生的是各水平之间的变异性，效应是随机效应。

单因素和无重复观测值的两因素数据因不涉及互作问题，效应均方只比误差均方多出一个效应项或方差项，计算时均以误差均方为分母。有重复观测值的两因素数据不同模型各项均方的数学期望和F统计量计算如下图：

excel公式法计算如下：

excel数据分析工具操作如下：

1、选择数据分析工具中，“方差分析：可重复双因素分析”

2、弹出对话框中，带标题选择数据区域，并在“每一样本的行数”处填写重复数，本例为3。

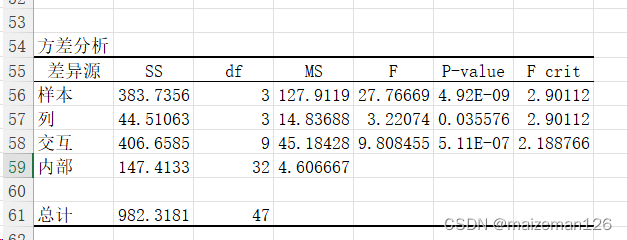
3、分析结果如下：

此法只能进行对固定模型的方差分析。