代码随想录day15｜层序遍历10道｜226.翻转二叉树｜101. 对称二叉树_node := queue.remove(queue.front()).(*treenode)

代码随想录day15

目录

代码随想录day15

二叉树层序遍历登场！

102、二叉树的层序遍历

107、二叉树的层序遍历II

199、二叉树的右视图

637、二叉树的层平均值

429、N叉树的层序遍历

515、在每个树行中找最大值

116/117 填充每一个节点的下一个右侧节点指针

104、二叉树的最大深度

111、二叉树的最小深度

226、翻转二叉树

101、对称二叉树

---

二叉树层序遍历登场！

学会二叉树的层序遍历，可以一口气打完以下十题：

• 102.二叉树的层序遍历
• 107.二叉树的层次遍历II
• 199.二叉树的右视图
• 637.二叉树的层平均值
• 429.N叉树的层序遍历
• 515.在每个树行中找最大值
• 116.填充每个节点的下一个右侧节点指针
• 117.填充每个节点的下一个右侧节点指针II
• 104.二叉树的最大深度
• 111.二叉树的最小深度

102、二叉树的层序遍历

        给你二叉树的根节点 root ，返回其节点值的 层序遍历 。 （即逐层地，从左到右访问所有节点）。

思路：

我们之前讲过了三篇关于二叉树的深度优先遍历的文章：

• 二叉树：前中后序递归法
• 二叉树：前中后序迭代法
• 二叉树：前中后序迭代方式统一写法
• 接下来我们再来介绍二叉树的另一种遍历方式：层序遍历。
• 层序遍历一个二叉树。就是从左到右一层一层的去遍历二叉树。这种遍历的方式和我们之前讲过的都不太一样。需要借用一个辅助数据结构即队列来实现，队列先进先出，符合一层一层遍历的逻辑，而是用栈先进后出适合模拟深度优先遍历也就是递归的逻辑。而这种层序遍历方式就是图论中的广度优先遍历，只不过我们应用在二叉树上。
• 使用队列实现二叉树广度优先遍历，动画如下：

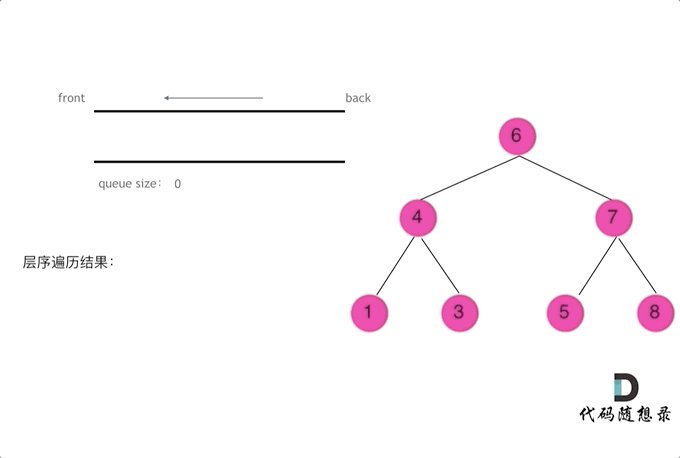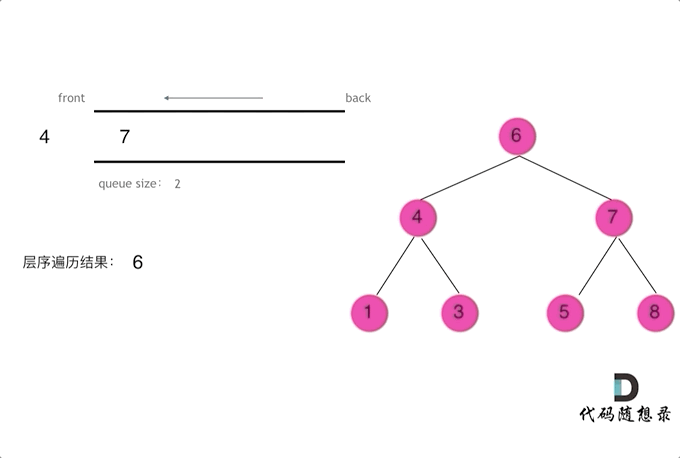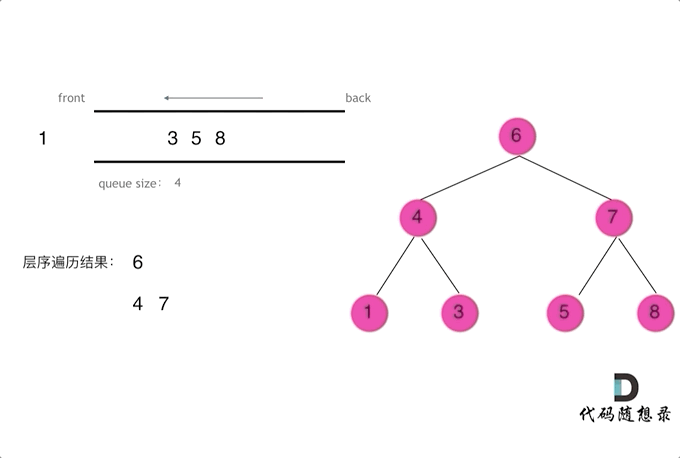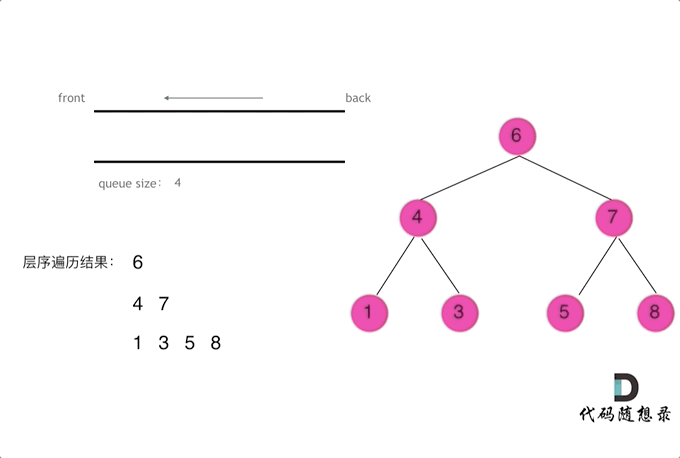
这样就实现了层序从左到右遍历二叉树。

本题代码如下：这份代码也可以作为二叉树层序遍历的模板，打十个就靠它了

func levelOrder(root *TreeNode) [][]int {
    res := [][]int{}
    if root == nil {
        return res
    }
    queue := list.New()    // 用list模拟队列
    queue.PushBack(root)    // 首先把root放进队列
    var temp []int    // 需要用到一个用来临时存储每一层值的切片。
    
    for queue.Len() > 0 {    // 循环条件是队列里面还有元素
        length := queue.Len()    // 每一层的长度。
        for i:=0;i<length;i++{    // 遍历每一层的东西。
            node := queue.Remove(queue.Front()).(*TreeNode)    // Pop元素，pop完要判断该元素有没有左右节点，有的话要push进去
            temp = append(temp, node.Val)
            if node.Left != nil {
                queue.PushBack(node.Left)
            }
            if node.Right != nil {
                queue.PushBack(node.Right)
            }
        }
        res = append(res,temp)    // 取出该层的值放进res里面
        temp = []int{}    // temp清空，下一层继续使用。
    }
    return res
}

        此时我们就掌握了二叉树的层序遍历了，那么如下九道力扣上的题目，只需要修改模板的两三行代码（不能再多了），便可打倒！

107、二叉树的层序遍历II

        给定一个二叉树，返回其节点值自底向上的层次遍历。 （即按从叶子节点所在层到根节点所在的层，逐层从左向右遍历）

 思路：

        思路就是按照层序遍历的模板遍历后，把res数组前后交换一下就可以了。

func levelOrderBottom(root *TreeNode) [][]int {
    res := [][]int{}
    if root == nil {
        return [][]int{}
    }
    queue := list.New()
    queue.PushBack(root)
    var temp []int
    for queue.Len() > 0 {
        length := queue.Len()
        for i:=0;i<length;i++{
            node := queue.Remove(queue.Front()).(*TreeNode)
            temp = append(temp, node.Val)
            if node.Left != nil {
                queue.PushBack(node.Left)
            }
            if node.Right != nil {
                queue.PushBack(node.Right)
            }
        }
        res = append(res, temp)
        temp = []int{}
    }
//重要代码，翻转res数组
    for i:=0;i<len(res)/2;i++{    
        res[i],res[len(res)-i-1] = res[len(res)-i-1], res[i]
    }
    return res
}

199、二叉树的右视图

        给定一棵二叉树，想象自己站在它的右侧，按照从顶部到底部的顺序，返回从右侧所能看到的节点值。

思路：

        按照层序遍历模板做，然后取res数组中的每一个数组的最后一位就行。

func rightSideView(root *TreeNode) []int {
    res := [][]int{}
    if root == nil {
        return []int{}
    }
    queue := list.New()
    queue.PushBack(root)
    var temp []int
    for queue.Len() > 0 {
        length := queue.Len()
        for i:=0;i<length;i++{
            node := queue.Remove(queue.Front()).(*TreeNode)
            temp = append(temp, node.Val)
            
            if node.Left != nil {
                queue.PushBack(node.Left)
            }
            if node.Right != nil {
                queue.PushBack(node.Right)
            }
        }
        res = append(res, temp)
        temp = []int{}
    }
// 将每层的最后一个节点的值放进last_res。
    last_res := []int{}
    for i:=0;i<len(res);i++{
        last_res = append(last_res, res[i][len(res[i])-1])
    }
    return last_res
}
 
 
// 更新代码
func rightSideView(root *TreeNode) []int {
	if root == nil {
		return nil
	}
	ans := make([]int,0)
	queue := list.New()
	queue.PushBack(root)
	for queue.Len() != 0 {
		length := queue.Len()
		temp := []int{}
		for i:=0;i<length;i++{
			node := queue.Remove(queue.Front()).(*TreeNode)
			temp = append(temp, node.Val)
			if node.Left != nil {
				queue.PushBack(node.Left)
			}
			if node.Right != nil {
				queue.PushBack(node.Right)
			}
		}
		ans = append(ans, temp[len(temp)-1])
	}
	return ans
}

637、二叉树的层平均值

        给定一个非空二叉树, 返回一个由每层节点平均值组成的数组。

思路：

        按照层序遍历的模板遍历，然后对res数组每层的值取平均值就可以了啊。

// 更新代码
func averageOfLevels(root *TreeNode) []float64 {
    var ans []float64
 
    queue := list.New()
    queue.PushBack(root)
    for queue.Len() != 0 {
        layerLen := queue.Len()
        
        var temp float64 = 0
        var count float64 = 0
        for i:=0;i<layerLen;i++{
            count++
            node := queue.Remove(queue.Front()).(*TreeNode)
            temp += float64(node.Val)
            if node.Left != nil {
                queue.PushBack(node.Left)
            }
            if node.Right != nil {
                queue.PushBack(node.Right)
            }
        }
        ans = append(ans,temp/count)
    }
    return ans
}
 
 
 
 
// 老代码
func averageOfLevels(root *TreeNode) []float64 {
    res := [][]int{}
    if root == nil {
        return []float64{}
    }
    queue := list.New()
    queue.PushBack(root)
    var temp []int
    for queue.Len() > 0 {
        length := queue.Len()
        for i:=0;i<length;i++{
            node := queue.Remove(queue.Front()).(*TreeNode)
            temp = append(temp,node.Val)
            if node.Left != nil {
                queue.PushBack(node.Left)
            }
            if node.Right != nil {
                queue.PushBack(node.Right)
            }
        }
        res = append(res,temp)
        temp = []int{}
    }
 
//此题重要代码
    var last_res []float64
    var sum int
    for i:=0;i<len(res);i++{
        for j:=0;j<len(res[i]);j++ {
            sum += res[i][j]
        }
        tmp := float64(sum)/float64(len(res[i]))
        last_res = append(last_res, tmp)
        sum = 0    //每层算完后清空
    }
    return last_res
}
 
 

429、N叉树的层序遍历

        给定一个 N 叉树，返回其节点值的层序遍历。 (即从左到右，逐层遍历)。

例如，给定一个 3叉树 :

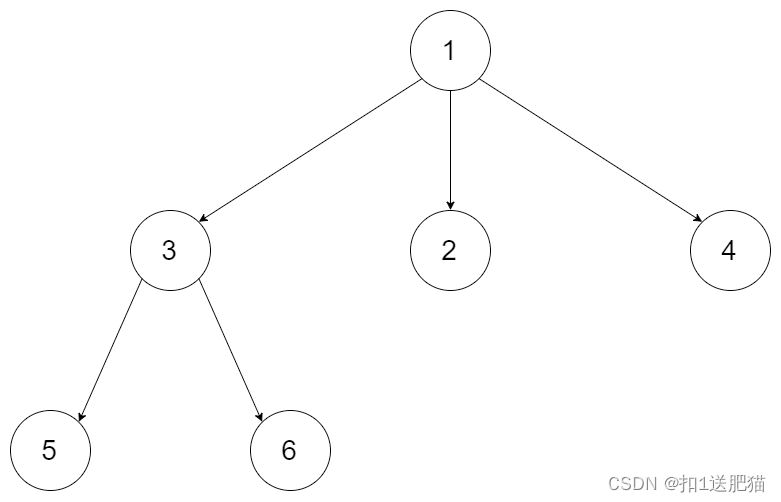
返回其层序遍历:

[[1],[3,2,4],[5,6]]

思路:

         这道题依旧是模板题，只不过一个节点有多个孩子了，就是以前是PushBack进left和right，现在是PushBack进Children[j]。

func levelOrder(root *Node) [][]int {
    res := [][]int{}
    if root == nil {
        return res
    }
    queue := list.New()
    queue.PushBack(root)
    var temp []int
    for queue.Len() > 0 {
        length := queue.Len()
        for i:=0;i<length;i++{
            node := queue.Remove(queue.Front()).(*Node)
            temp = append(temp, node.Val)
            for j:=0;j<len(node.Children);j++{    //重要代码，PushBack多个孩子节点
                queue.PushBack(node.Children[j])
            }
        }
        res = append(res, temp)
        temp = []int{}
    }
    return res
}
 
/**
 * Definition for a Node.
 * type Node struct {
 *     Val int
 *     Children []*Node
 * }
 */
 
func levelOrder(root *Node) [][]int {
    var ans [][]int
    if root == nil {
        return ans
    }
    queue := list.New()
    queue.PushBack(root)
    for queue.Len() != 0 {
        layerLen := queue.Len()
        var temp []int
        for i :=0;i<layerLen;i++{
            node := queue.Remove(queue.Front()).(*Node)
            temp = append(temp, node.Val)
            for i:=0; i<len(node.Children) && node.Children != nil;i++ {
                queue.PushBack(node.Children[i])
            }
        }
        ans = append(ans, temp)
    }
    return ans
}

515、在每个树行中找最大值

        您需要在二叉树的每一行中找到最大的值。

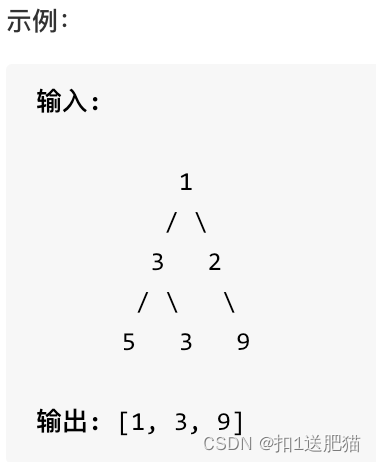
思路：

        层序遍历模板遍历，然后取每一层的最大值

// 更新代码
func largestValues(root *TreeNode) []int {
    var ans []int
    if root == nil {
        return ans
    }
    queue := list.New()
    queue.PushBack(root)
    for queue.Len() != 0 {
        layerLen := queue.Len()
        var temp int = math.MinInt32
        for i:=0;i<layerLen;i++{
            node := queue.Remove(queue.Front()).(*TreeNode)
            if node.Val > temp {
                temp = node.Val
            }
            if node.Left != nil {
                queue.PushBack(node.Left)
            }
            if node.Right != nil {
                queue.PushBack(node.Right)
            }
        }
        ans = append(ans, temp)
    }
    return ans
}
 
 
 
// 老代码
func largestValues(root *TreeNode) []int {
    res := [][]int{}
    if root == nil {
        return []int{}
    }
    queue := list.New()
    queue.PushBack(root)
    var temp []int
    for queue.Len() > 0 {
        length := queue.Len()
        for i:=0;i<length;i++{
            node := queue.Remove(queue.Front()).(*TreeNode)
            temp = append(temp,node.Val)
            if node.Left != nil {
                queue.PushBack(node.Left)
            }
            if node.Right != nil {
                queue.PushBack(node.Right)
            }
        }
        res = append(res,temp)
        temp = []int{}
    }
//取二维切片里面的每个切片的最大值
    last_res := []int{}
    for i := 0; i < len(res); i++ {
        last_res = append(last_res, max(res[i]))
    }
    return last_res
}
 
//max函数，用来取一个切片中的最大值。
func max(vals []int) int {
    max := int(math.Inf(-1))
    for _, v := range vals {
        if v > max {
            max = v
        }
    }
    return max
}

116/117 填充每一个节点的下一个右侧节点指针

        给定一个完美二叉树，其所有叶子节点都在同一层，每个父节点都有两个子节点。二叉树定义如下：

type Node struct {
  Val int
  Left *Node
  Right *Node
  Next *Node
}

        填充它的每个 next 指针，让这个指针指向其下一个右侧节点。如果找不到下一个右侧节点，则将 next 指针设置为 NULL。

初始状态下，所有 next 指针都被设置为 NULL

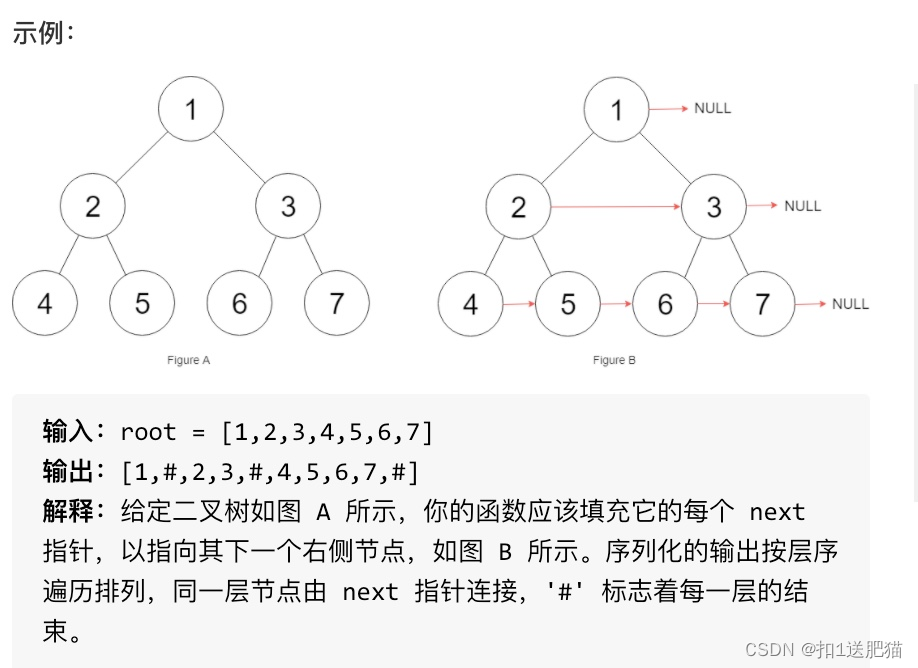
思路：

        层序遍历模板遍历。然后对每层的元素的Next指向右边就好了,每层的最后一个元素不需要指，因为默认指向了NULL。

func connect(root *Node) *Node {
    if root == nil { //防止为空
        return root
    }
    queue := list.New()
    queue.PushBack(root)
    tmpArr := make([]*Node, 0)
    for queue.Len() > 0 {
        length := queue.Len() //保存当前层的长度，然后处理当前层（十分重要，防止添加下层元素影响判断层中元素的个数）
        for i := 0; i < length; i++ {
            node := queue.Remove(queue.Front()).(*Node) //出队列
            if node.Left != nil {
                queue.PushBack(node.Left)
            }
            if node.Right != nil {
                queue.PushBack(node.Right)
            }
            tmpArr = append(tmpArr, node) //将值加入本层切片中
        }
        if len(tmpArr) > 1 {
            // 遍历每层元素,指定next
            for i := 0; i < len(tmpArr)-1; i++ {
                tmpArr[i].Next = tmpArr[i+1]
            }
        }
        tmpArr = []*Node{} //清空层的数据
    }
    return root
}

104、二叉树的最大深度

        给定一个二叉树，找出其最大深度。二叉树的深度为根节点到最远叶子节点的最长路径上的节点数。

说明: 叶子节点是指没有子节点的节点。
示例：
给定二叉树 [3,9,20,null,null,15,7]，返回它的最大深度 3 。

思路：

        使用迭代法的话，使用层序遍历是最为合适的，因为最大的深度就是二叉树的层数，和层序遍历的方式极其吻合。

在二叉树中，一层一层的来遍历二叉树，记录一下遍历的层数就是二叉树的深度，如图所示：

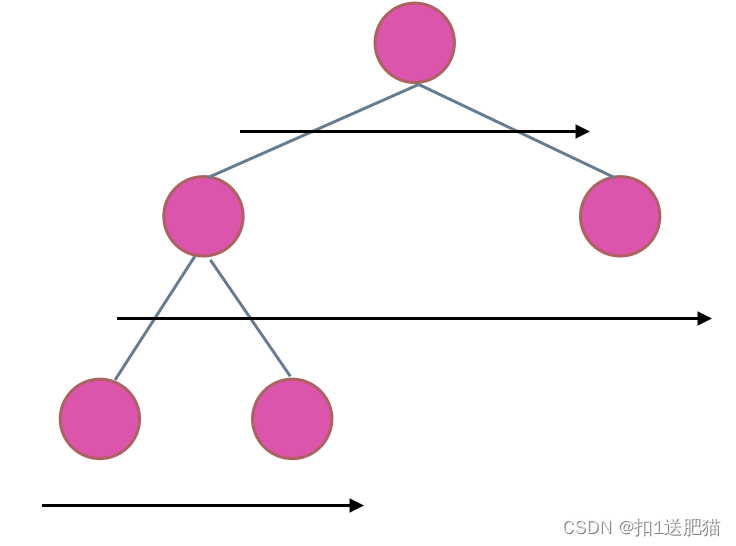
所以这道题的迭代法就是一道模板题，可以使用二叉树层序遍历的模板来解决的。

func maxDepth(root *TreeNode) int {
    ans := 0
    if root == nil {
        return ans
    }
    queue := list.New()
    queue.PushBack(root)
    for queue.Len() > 0 {
        length := queue.Len()
        for i:=0;i<length;i++{
            node := queue.Remove(queue.Front()).(*TreeNode)
            if node.Left != nil {
                queue.PushBack(node.Left)
            }
            if node.Right != nil {
                queue.PushBack(node.Right)
            }
        }
        ans++    //重要代码，每遍历完一层就记下来一下
    }
    return ans
}

111、二叉树的最小深度

        相对于 104.二叉树的最大深度 ，本题还也可以使用层序遍历的方式来解决，思路是一样的。

        需要注意的是，只有当左右孩子都为空的时候，才说明遍历的最低点了。如果其中一个孩子为空则不是最低点

func minDepth(root *TreeNode) int {
    ans:=1
    if root==nil{
        return 0
    }
    queue:=list.New()
    queue.PushBack(root)
    for queue.Len()>0{
        length:=queue.Len()
        for i:=0;i<length;i++{
            node:=queue.Remove(queue.Front()).(*TreeNode)
            if node.Left==nil&&node.Right==nil{    // 重要代码，只有左右节点都不存在的时候就是最小深度。
                return ans 
            }
            if node.Left!=nil{
                queue.PushBack(node.Left)
            }
            if node.Right!=nil{
                queue.PushBack(node.Right)
            }
        }
        ans++//记录层数
    }
    return ans
}

以上就是10道层序遍历的模板题目啦。

226、翻转二叉树

        翻转一棵二叉树。

思路：

        我们之前介绍的都是各种方式遍历二叉树，这次要翻转了，感觉还是有点懵逼。这得怎么翻转呢？如果要从整个树来看，翻转还真的挺复杂，整个树以中间分割线进行翻转，如图：

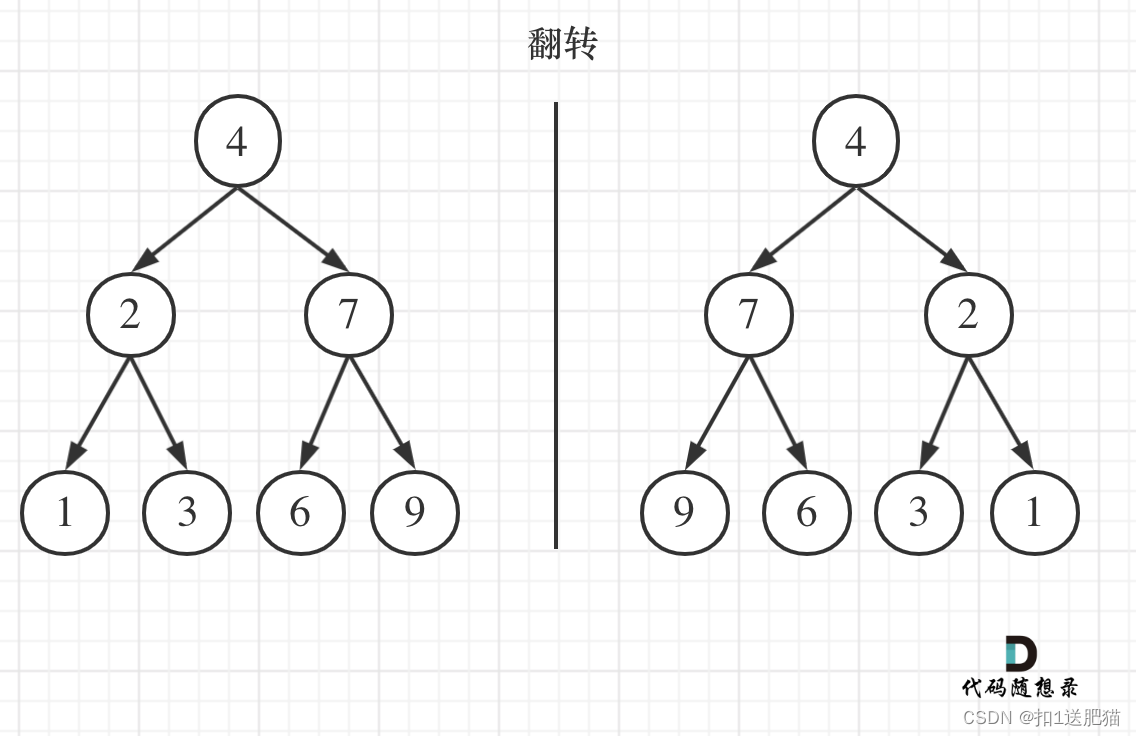
        可以发现想要翻转它，其实就把每一个节点的左右孩子交换一下就可以了。关键在于遍历顺序，前中后序应该选哪一种遍历顺序？ （一些同学这道题都过了，但是不知道自己用的是什么顺序）遍历的过程中去翻转每一个节点的左右孩子就可以达到整体翻转的效果。

        注意只要把每一个节点的左右孩子翻转一下，就可以达到整体翻转的效果

        这道题目使用前序遍历和后序遍历都可以，唯独中序遍历不方便，因为中序遍历会把某些节点的左右孩子翻转了两次！建议拿纸画一画，就理解了

        那么层序遍历可以不可以呢？依然可以的！只要把每一个节点的左右孩子翻转一下的遍历方式都是可以的！

//递归版本的前序遍历
func invertTree(root *TreeNode) *TreeNode {
    if root ==nil{
        return nil
    }
    root.Left,root.Right=root.Right,root.Left    //交换
    invertTree(root.Left)
    invertTree(root.Right)
    return root
}
 
//递归版本的后序遍历
func invertTree(root *TreeNode) *TreeNode {
    if root==nil{
        return root
    }
    invertTree(root.Left)//遍历左节点
    invertTree(root.Right)//遍历右节点
    root.Left,root.Right=root.Right,root.Left//交换
    return root
}
 
//递归版本的中序遍历做不了
 
 
 
 
//层序遍历
func invertTree(root *TreeNode) *TreeNode {
    if root == nil {
        return nil    
    }
    queue := list.New()
    queue.PushBack(root)
    for queue.Len() > 0 {
        length := queue.Len()
        for i:=0;i<length;i++{
            node := queue.Remove(queue.Front()).(*TreeNode)
            node.Left, node.Right = node.Right, node.Left    //交换
            if node.Left != nil {
                queue.PushBack(node.Left)            
            }        
            if node.Right != nil {
                queue.PushBack(node.Right)            
            }
        }    
    }
    return root
}

101、对称二叉树

        给定一个二叉树，检查它是否是镜像对称的

思路：

        首先想清楚，判断对称二叉树要比较的是哪两个节点，要比较的可不是左右节点！

        对于二叉树是否对称，要比较的是根节点的左子树与右子树是不是相互翻转的，理解这一点就知道了其实我们要比较的是两个树（这两个树是根节点的左右子树），所以在递归遍历的过程中，也是要同时遍历两棵树。

那么如何比较呢？比较的是两个子树的里侧和外侧的元素是否相等。如图所示：

        那么遍历的顺序应该是什么样的呢？本题遍历只能是“后序遍历”，因为我们要通过递归函数的返回值来判断两个子树的内侧节点和外侧节点是否相等。

        正是因为要遍历两棵树而且要比较内侧和外侧节点，所以准确的来说是一个树的遍历顺序是左右中，一个树的遍历顺序是右左中。

        但都可以理解算是后序遍历，尽管已经不是严格上在一个树上进行遍历的后序遍历了。

        其实后序也可以理解为是一种回溯，当然这是题外话，讲回溯的时候会重点讲的。说到这大家可能感觉我有点啰嗦，哪有这么多道理，上来就干就完事了。别急，我说的这些在下面的代码讲解中都有身影。

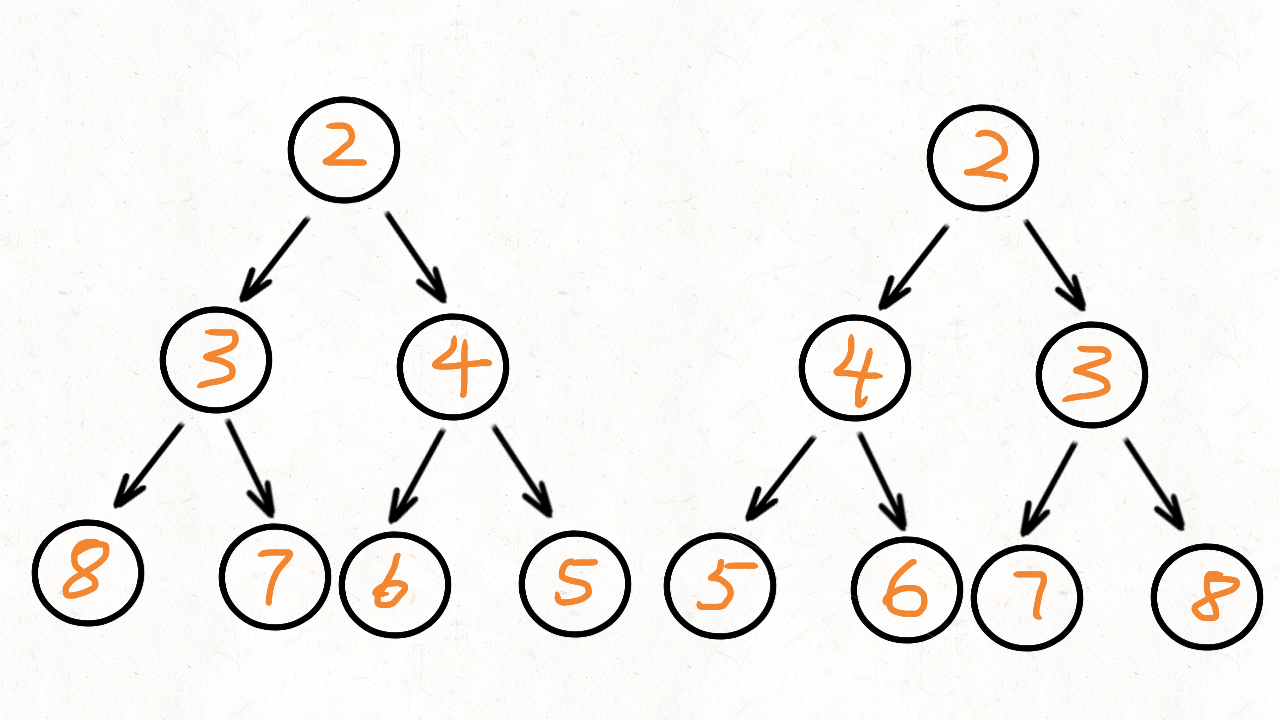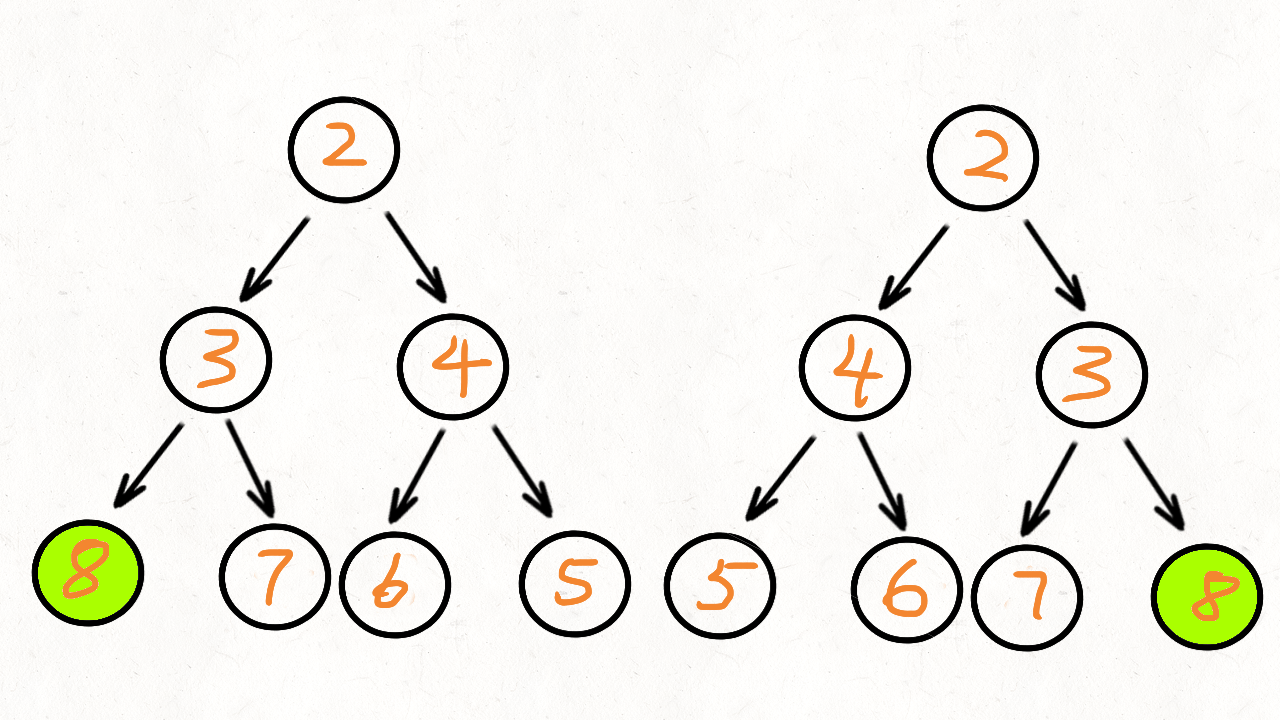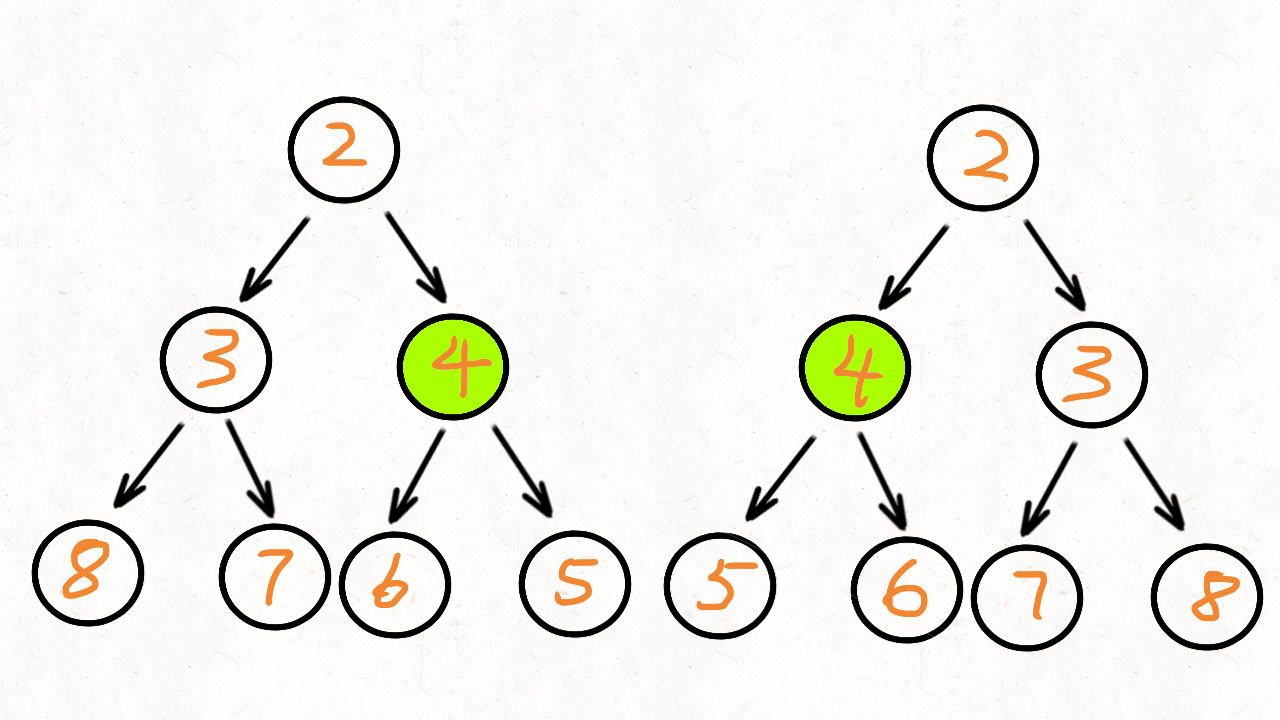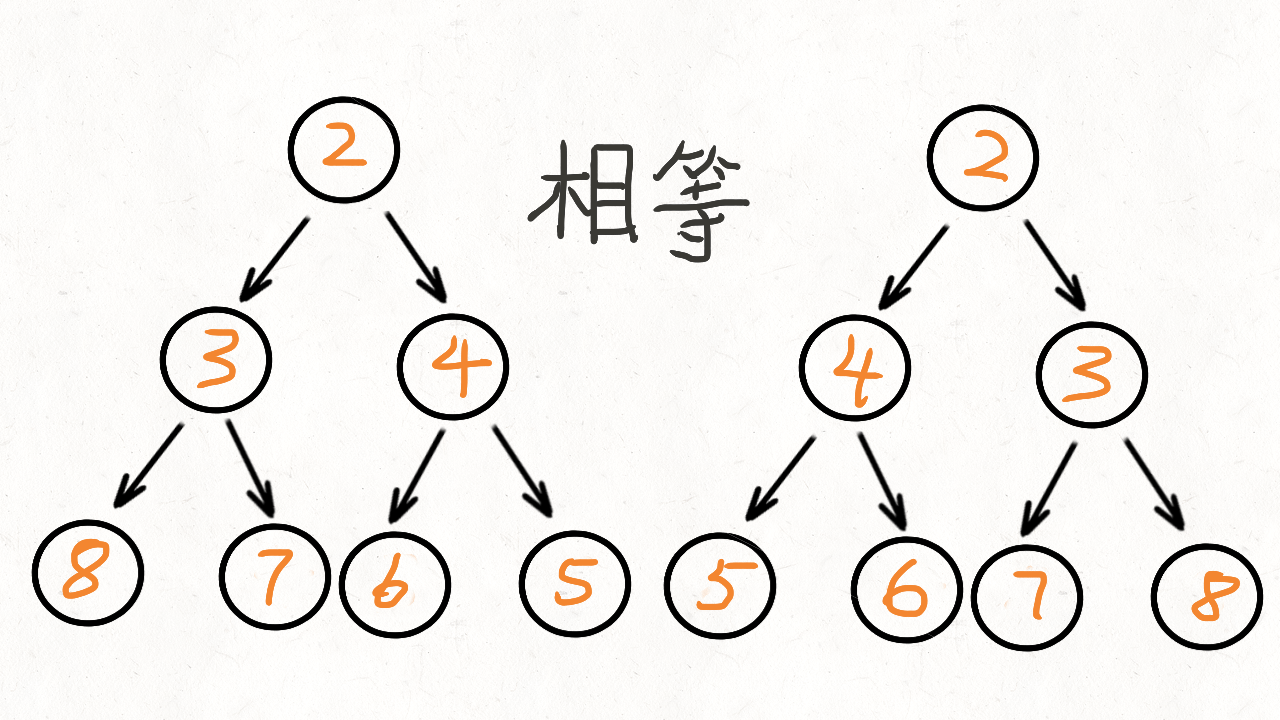
递归法：

递归三部曲

1、确定递归函数的参数和返回值

        因为我们要比较的是根节点的两个子树是否是相互翻转的，进而判断这个树是不是对称树，所以要比较的是两个树，参数自然也是左子树节点和右子树节点。返回值自然是bool类型。

func compare(left *TreeNode, right *TreeNode)

2、确定终止条件

        节点为空的情况有：（注意我们比较的其实不是左孩子和右孩子，所以如下我称之为左节点右节点）

• 左右节点都为空，对称，返回true
• 左节点为空，右节点不为空，不对称，return false
• 左不为空，右为空，不对称 return false

此时已经排除掉了节点为空的情况，那么剩下的就是左右节点不为空：

• 左右都不为空，比较节点数值，不相同就return false

此时左右节点不为空，且数值也不相同的情况我们也处理了。

代码如下：

  if left == nil && right == nil {    // 左右都为空，true
    return true
  }
  if left == nil || right == nil {   // 左右只有一个为空，另一个不为空，不对称，false 
    return false
  }
  if left.Val != right.Val {    // 左右都不为空，但value不相等，false
    return false
  }

3、确定单层递归的逻辑

此时才进入单层递归的逻辑，单层递归的逻辑就是处理 左右节点都不为空，且数值相同的情况。

• 比较二叉树外侧是否对称：传入的是左节点的左孩子，右节点的右孩子。
• 比较内测是否对称，传入左节点的右孩子，右节点的左孩子。
• 如果左右都对称就返回true ，有一侧不对称就返回false 。

 return defs(left.Left, right.Right) && defs(right.Left, left.Right)

最后递归的Go整体代码如下：

func defs(left *TreeNode, right *TreeNode) bool {
  if left == nil && right == nil {
    return true
  }
  if left == nil || right == nil {
    return false
  }
  if left.Val != right.Val {
    return false
  }
  return defs(left.Left, right.Right) && defs(right.Left, left.Right)
}
func isSymmetric(root *TreeNode) bool {
    return defs(root.Left,root.Right)
}

今天到这里。