[蓝桥杯 2022 省 B] 统计子矩阵 （前缀和）

 原题传送门

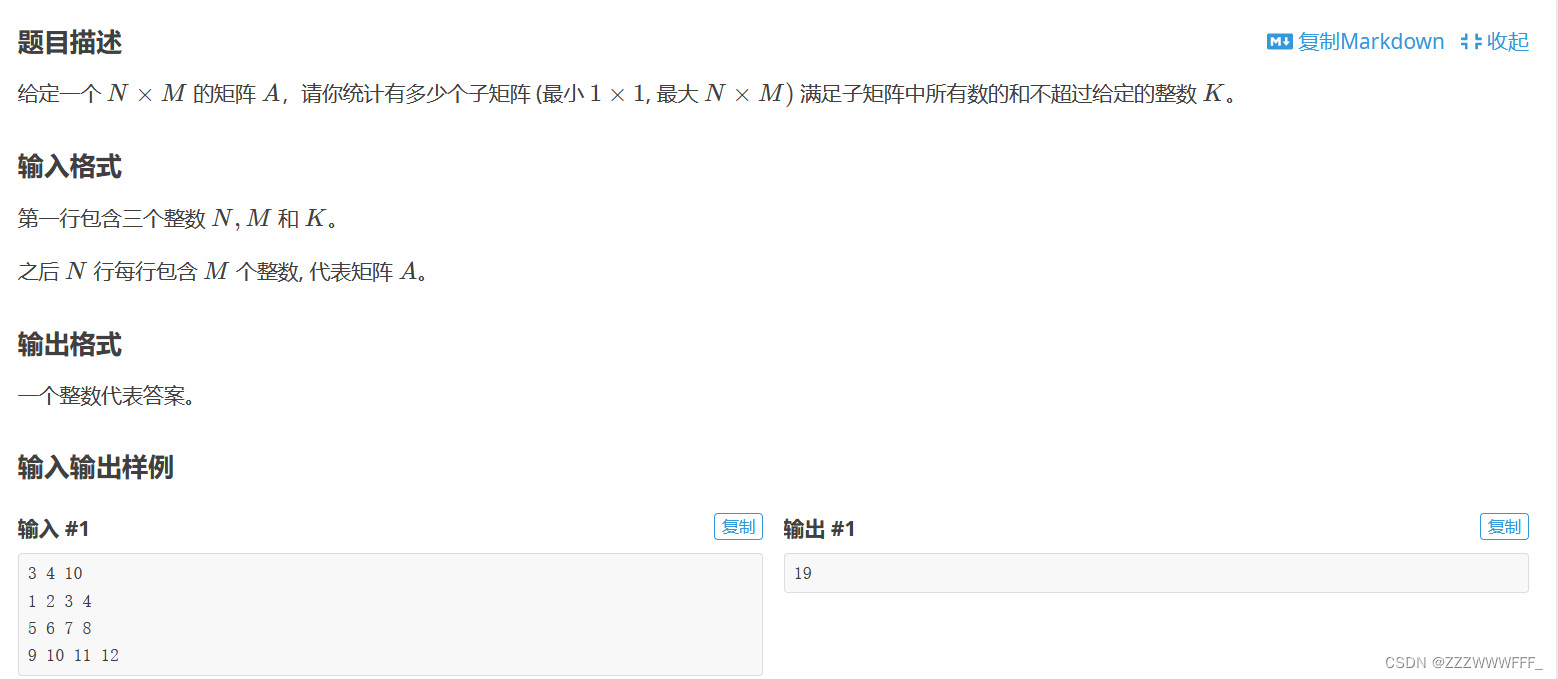
 该题第一眼给我的感觉就是要使用前缀和解决了

即利用前缀和枚举出所有可能的矩阵情况

这里假设以（1,1）点为起点求可能的所有子矩阵的和，我们定义一个数组temp[i][j]的值为（i,j）这个点到起点（x,y）所连成线的矩阵的权值（即矩阵内每个点的和），这里可以利用动态规划的思想，我们可以很容易想到tmep[i][j]=temp[i-1][j]+temp[i][j-1]-temp[i-1][j-1]

注意要保证数组不要越界

根据上面的思想，我们再枚举每一个点作为起点即可枚举出所有情况

容易知道这样的算法是时间复杂度是n^4的，不过该题的数据范围并不太大，因此还是能通过大部分样例

#include<iostream>
#include<cstring>
#define MAX 505
using namespace std;
 
int arr[MAX][MAX];
int n,m,k,ans=0;
 
void fun(int x,int y){//（x,y）为起点
	int temp[MAX][MAX];//前缀和数组
	for(int i=1;i<=n;i++){
		for(int j=1;j<=m;j++){//初始化
			temp[i][j]=arr[i][j];
		}
	}	
	for(int i=x;i<=n;i++){
		for(int j=y;j<=m;j++){//计算前缀和
			if(i-1>=x){//小心越界
				temp[i][j]+=temp[i-1][j];
			}
			if(j-1>=y){
				temp[i][j]+=temp[i][j-1];
			}
			if(i-1>=x&&j-1>=y){
				temp[i][j]-=temp[i-1][j-1];
			}
			if(temp[i][j]<=k){//对满足题意的矩阵进行计数
				ans++;
			}
		}
	}
//	for(int i=1;i<=n;i++){//测试代码 
//		for(int j=1;j<=m;j++){
//			cout<<temp[i][j]<<" "; 
//		}
//		cout<<endl;
//	}
} 
 
int main(){
	cin>>n>>m>>k;
	for(int i=1;i<=n;i++){
		for(int j=1;j<=m;j++){
			cin>>arr[i][j];
		}
	}
	for(int i=1;i<=n;i++){
		for(int j=1;j<=m;j++){//枚举起点 
			fun(i,j);
		}
	}	
	cout<<ans<<endl;
	return 0;
} 
 

 上述思路实际上还可以进行优化，不过我并没有想到，感兴趣的读者可以自行搜索