Acwing---867. 分解质因数 (Java)_优化后的模板题_java分解质因数优化版

原题链接

①. 题目

②. 思路

• 根据算术基本定理，不考虑排列顺序的情况下，每个正整数都能够以唯一的方式表示成它的质因数的乘积。
  

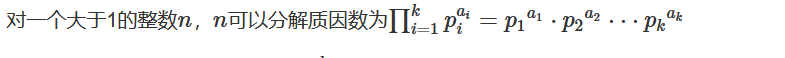
• 比如一个数16 在分解时先找到2这个质因子，然后由于16/2后还可以/2，所以会在2这个质因子上产生次方

• 不优化版本：从2~n 找到能整除的因子然后算次方

• 这里有个性质：n中最多只含有一个大于sqrt(n)的因子。于是我们发现最多只有一个大于sqrt(n)的因子，对其进行优化。先考虑比sqrt(n)小的，代码和质数的判定类似

• 最后如果n还是>1，说明这就是大于sqrt(n)的唯一质因子，输出即可。

③. 学习点

④. 代码实现

import java.util.*;

public class Main {
	/**
	 * 根据算术基本定理，不考虑排列顺序的情况下，每个正整数都能够以唯一的方式表示成它的质因数的乘积。
		n=p1^a1 * p2^a2 *p3^a3.....pn^an
		比如一个数16 在分解时先找到2这个质因子，然后由于16/2后还可以/2，所以会在2这个质因子上产生次方
		不优化版本：从2~n 找到能整除的因子然后算次方
		
		于是我们发现最多只有一个大于sqrt(n)的因子，对其进行优化。
		先考虑比sqrt(n)小的，代码和质数的判定类似
		最后如果n还是>1，说明这就是大于sqrt(n)的唯一质因子，输出即可。
	 * @param args
	 */
	public static void main(String[] args) {
		Scanner sc = new Scanner(System.in);
		int n = sc.nextInt();
		for (int i = 0; i <n; i++) {
			int temp = sc.nextInt();
			isPrime(temp);
		}
	}
	
	public static void isPrime(int n) {
		for(int i=2;i<=Math.sqrt(n);i++) {
			int count=0;
			while(n%i==0) {
				n/=i;
				count++;
			}
			if(count!=0) System.out.println(i+" "+count);
	}
	//最后如果n还是>1，说明这就是大于sqrt(n)的唯一质因子，输出即可。
		if(n>1) {
			System.out.println(n+" "+1);
		}
		System.out.println();

}
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41