人工智能导论(7)——人工神经网络(Machine Learning)_神经网络人工智能实验导论

---

一、 概述

学习能力是智能的重要标志之一。机器学习是人工智能的核心研究课题之一。

为方便记忆和回顾，根据个人学习，总结人工智能基础知识和思维导图形成系列。

二、 重点内容

• 基础知识
• 人工神经元
• 感知机
• BP反向传播算法
• 深度神经网络简介

三、 思维导图

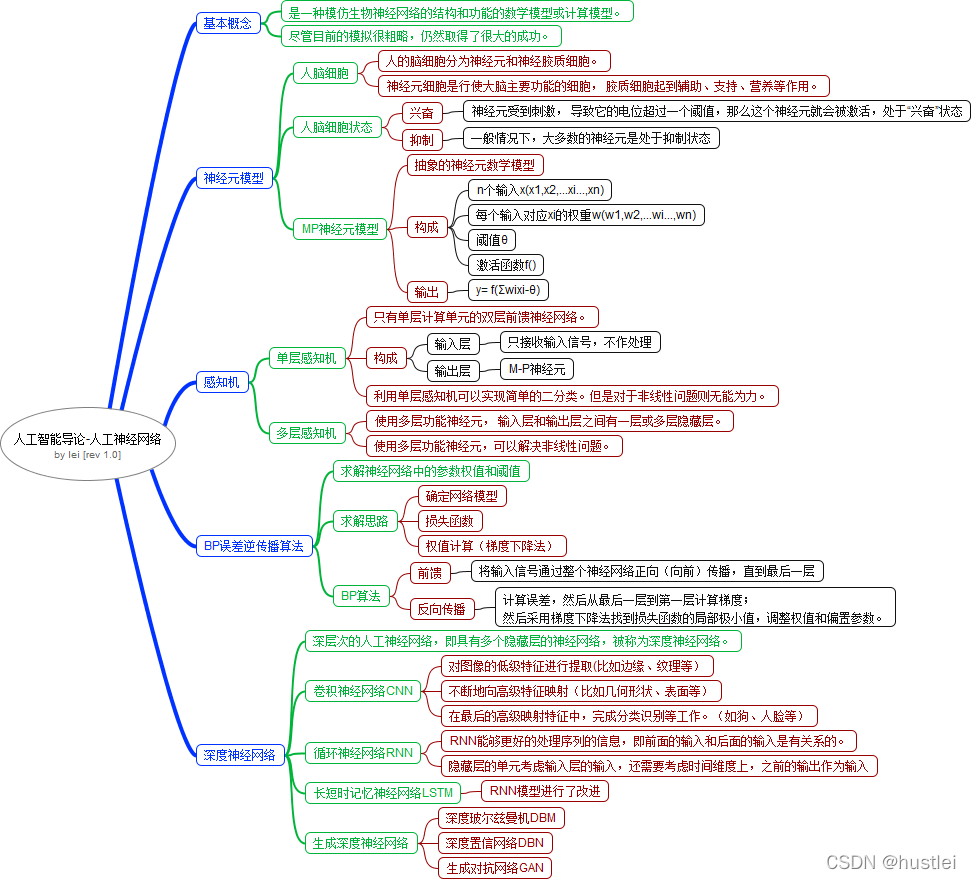
四、 重点知识笔记

概述

人工神经网络（Artificial Neural Network，ANN）简称神经网络（Neural Network，NN）的发展源于研究人员对大脑神经网络的结构模拟。是一种模仿生物神经网络的结构和功能的数学模型或计算模型。尽管目前的模拟很粗略，仍然取得了很大的成功。

人工神经网络在视觉、听觉等感知智能，机器翻译、语音识别和聊天机器人等语言智能，
棋类、游戏等决策类应用，以及艺术创造等方面所取得的重要成就，
证明了联结主义路线的正确性。

1. 神经元模型

人的脑细胞分为神经元和神经胶质细胞。神经元细胞是行使大脑主要功能的细胞，胶质细胞起到辅助、支持、营养等作用。

生物学上，神经元有两种状态：兴奋和抑制。
一般情况下，大多数的神经元是处于抑制状态，但是一旦某个神经元受到刺激，导致它的电位超过一个阈值，那么这个神经元就会被激活，处于“兴奋”状态，进而向其他的神经元传播化学物质（其实就是信息）。

1943年，美国心理学家麦卡洛克和皮茨提出了生物神经元的抽象数学模型——MP模型：

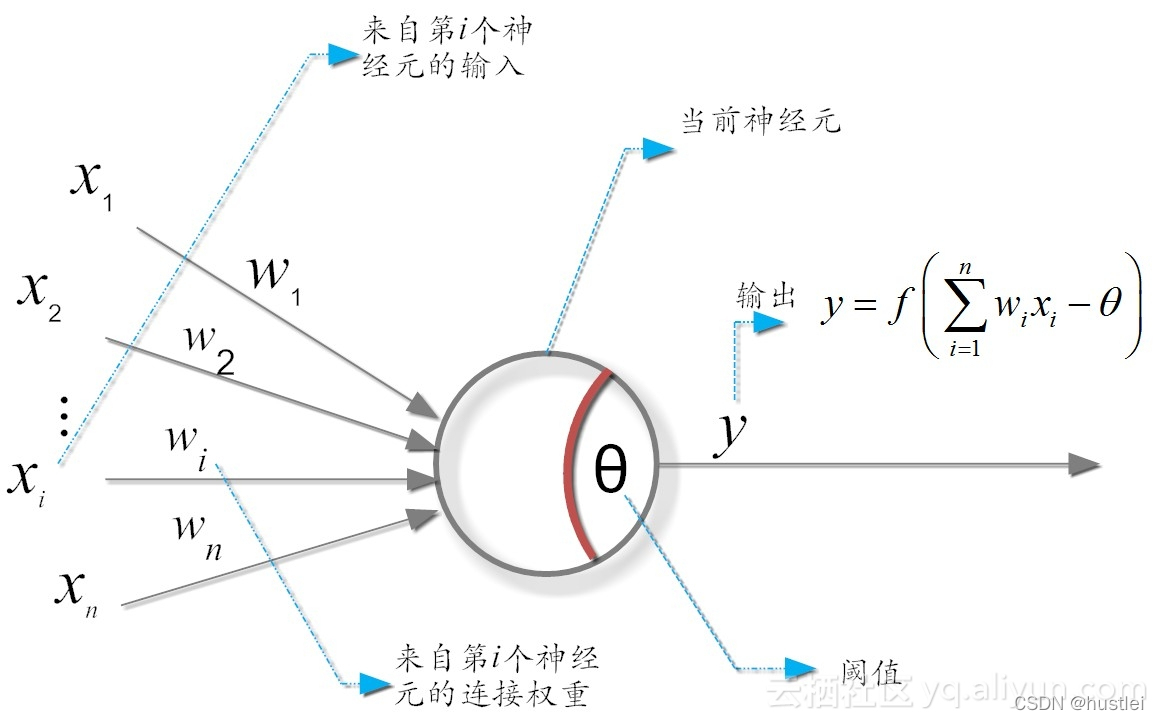
从上图可以看出，神经元的输出：

y = f(Σwixi-θ)
其中：θ为神经元的激活阈值，函数f(⋅)被称为是激活函数。
1
2

神经元的工作模型存在“激活（1）”和“抑制（0）”等两种状态的跳变，理想型的激活函数（activation functions）应该是的阶跃函数，但在实际使用中，这种函数具有不光滑、不连续等众多不“友好”的特性。因为在训练网络权重时，通常依赖对某个权重求偏导、寻极值，不光滑、不连续通常意味着该函数无法“连续可导”。

所以，我们一般用Sigmoid函数来代替阶跃函数。

常用的激活函数有：

• 阈值函数：该函数通常也称为阶跃函数，此时神经元的输出取１或０
• Sigmoid函数：也称为对数S形函数，输出介于0~1之间
  • 常被输出在０-１范围的信号选用，它是神经元中使用最为广泛的激活函数
• 线性函数：该函数可以在输出结果为任意值时作为输出神经元的激活函数
  • 但是当网络复杂时，线性激活函数大大降低网络的收敛性，故一般较少采用
• 双曲正切S形函数：类似于被平滑的阶跃函数，以原点对称，其输出介于-１１之间
  • 常常被要求为输出在-１１范围的信号选用

自MP模型被提出以后，研究人员提出了很多不同类型和结构的人工神经网络。
最早的人工神经网络就是感知机模型。

2. 单层感知机

单层感知机是一个只有单层计算单元的前馈神经网络。

前馈神经网络是一种最简单的神经网络，各神经元分层排列。每个神经元只与前一层的
神经元相连。接收前一层的输出，并输出给下一层。各层间没有反馈。
前馈神经网络是目前应用最广泛、发展最迅速的人工神经网络之一。

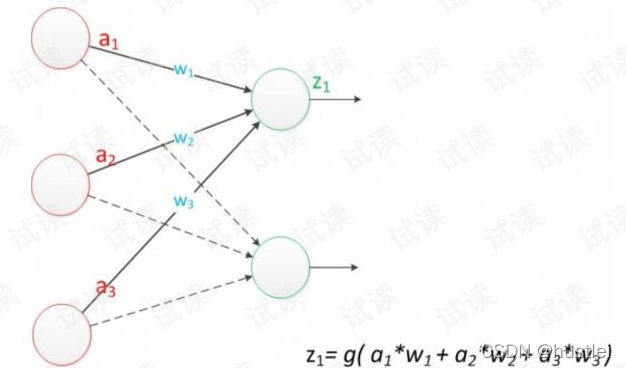
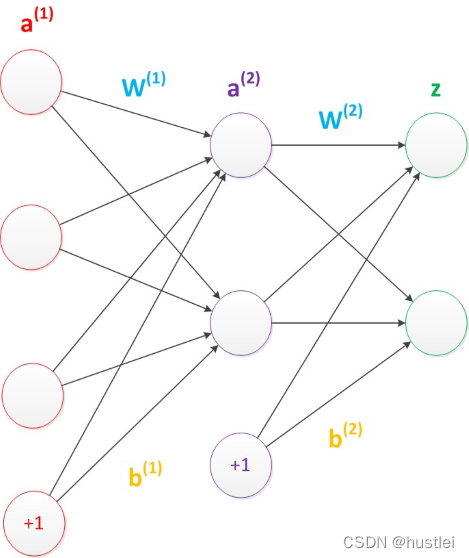
上图为一个典型的单层感知机模型，a(a1,a2,a3)为输入，w(w1,w2,w3)为权值，z为输出。

单层感知机由两层构成，输入层接收外界输入信号后，传递给输出层，输出层是M-P神经元。单层感知机只有一层功能神经元（只有输出层神经元进行计算处理）。

利用单层感知机可以实现简单的二分类。但是对于非线性问题则无能为力。

3. 多层感知机

使用多层功能神经元，可以解决非线性问题。多层感知机使用多层功能神经元，输入层和输出层之间有一层或多层隐藏层。

• 输入层神经元仅接收输入，不进行函数处理
• 隐藏层和输出层包含功能神经元。

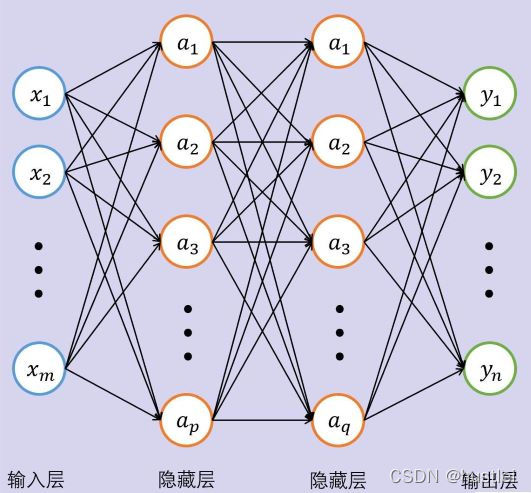
多层感知机是多层前馈神经网络。

M-P神经元的模型为y=f(wx+b)，但是前边所示的感知机实际上只是y=f(wx)，并没有处理偏置b。在实际的在神经网络的每个层次中，除了输出层以外，都会含有这样一个偏置单元。

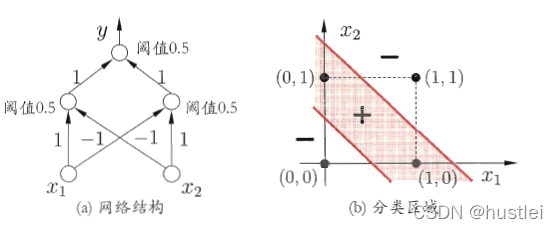
双层感知机可以很容易的解决非线性的异或问题。

4. BP误差逆传播算法

感知机是前馈型人工神经网络模型，也是一种机器学习模型。

人工神经网络的学习过程，就是确定权值的过程，误差逆传播算法是最成功的求解算法之一。

以单层感知机为例：

最简单的单层感知机BP误差传播算法

1）确定网络模型

假设有2个输入，1个输出神经元，则模型相关参数为：

• 输入层输入：x1,x2(多个输入为x1,x2,…,xm)
• 输出层输出：y1(多个输出为y1,y2,…,yn)
• 权值：w1,w2(多个输入则为w1,w2,…wm)
• 偏置量：b（单层神经网络仅有一个偏置值，每层网络公用一个偏置节点）

则模型用公式表示y1=f(w1x1+w2x2+b)

以房价和面积、房龄的关系为例。面积、房龄为输入，房价为输出。

取f(w1x1+w2x2+b)=w1x1+w2x2+b，则化为线性函数。

2）训练思路

训练神经网络的思路：

• 已知一组输入输出的数据(x11,x22)(x12,x22)...(x1i,x2i)
• 找到权值w(w1,w2)，让y=w1x1+w2x2+b计算的输出与已知输出最接近

3）损失函数loss

通常我们需要收集一组已知输出的数据。

以房价为例：已知样本数为n，第i个样本输入(面积i,房龄i)为(x1i,x2i)，第i个房屋的真实价格是yi。对第i样本，根据感知机模型计算的房价为yoi=w1*x1i+w2*x2i+b

房屋的真实价格与计算价格之间存在一定的误差，这里我们使用平方误差去进行计算。

lossi = (yoi-yi)**2
1

在机器学习里，将衡量误差的函数称为损失函数。通常，使用训练数据集中所有样本误差的平均来衡量模型预测误差。

loss = Σlossi/n = Σ((w1*x1i+w2*x2i+b - yoi)**2)/n
1

4）权值w的计算（梯度下降法）

神经网络的训练目的是计算出权值w和偏置值b，使得用得到的w和b计算的输出与已知的输出最相近。（训练得到的w和b计算的房价与已知的房价误差最小。）

求权值w和偏置b的问题变为求loss的极小值问题。平方误差函数本身是一个y=x**2的形式，是一个开口向上的抛物线方程。在任意一点计算梯度，即方程导数，根据梯度方向调整参数，就能逐步找到最小点。

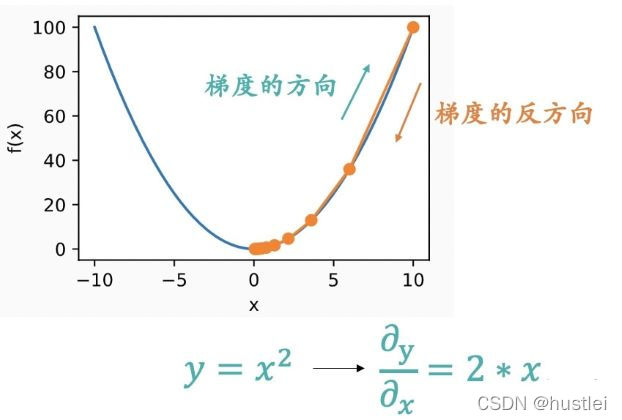
在神经网络训练时，x，y是已知值，w，b是未知值。根据以下步骤可以计算得到loss最小的w，b值。这个过程也就是调参。

1. 随机给定一个w，b的初始值，比如w=1,b=0。根据样本计算loss。
2. 求出损失函数对w和b的梯度，即偏导数△w=∂loss/∂w，△b=∂loss/∂b
3. 根据梯度调整w，b。
   • w=w-α△w
   • b=b-α△b
   • α是为了防止步长太大，导致错过最小点而定的系数，通常小于1。在机器学习中被称为学习率。
4. 根据调整后的w，b，迭代执行2-3。直到得出最优的解，通常在loss变化量极小的时候就认为找到最优解了。

BP反向传播算法

BP算法的训练过程和上述过程一样，是一个反复迭代以修正权值参数的过程，分为两个阶段。

第一阶段，是将输入信号通过整个神经网络正向（向前）传播，直到最后一层。这个过程称为前馈。
第二阶段，计算误差，然后从最后一层到第一层计算梯度；然后采用梯度下降法找到损失函数的局部极小值，调整权值和偏置参数。

BP算法不仅可以用于多层前馈神经网络，还可以用于其他类型的神经网络，比如递归神经网络。

5. 深度神经网络简介

深层次的人工神经网络，即具有多个隐藏层的神经网络，被称为深度神经网络。

5.1 卷积神经网络CNN简介

卷积神经网络（CNN）是人工神经网络中的一种经典模型，在图像处理、人脸识别等计算机视觉方面得到了广泛应用。

CNN的核心思想是:

• 对图像的低级特征进行提取(比如边缘、纹理等）
• 不断地向高级特征映射（比如几何形状、表面等）
• 在最后的高级映射特征中，完成分类识别等工作。（如狗、人脸等）

稀疏连接、权值共享和特征提取

传统人工神经网络通常在各层之间采用全连接，即连接层中的每个结点都与上一层的所有结点相连。权值数量非常多，计算难度极大。为此，CNN使用稀疏连接（Sparse Connectivity），即连接层中的每个节点仅与上一层的少数节点相连。

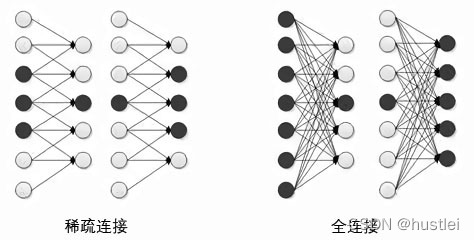
图像处理输入数据量很大，以100×100像素，共10000个像素。在全连接情况下，每个像素都与下一层神经元连接，共需要10000个权值参数。
在稀疏连接下，每个神经元只对局部图像进行处理，同一层神经元共享权值时，权值参数降低了很多。

以每次卷积运算处理图像局部10×10个像素时，共需100个权值参数。

提取特征的过程是把原始图像（比如100×100），对每个图像局部（10×10），逐步进行卷积运算，得到新的图像数据。通常卷积运算就是用一个指定矩阵对给定数据进行变换的过程。

5.2 循环神经网络RNN简介

循环神经网络（Recurrent Neural Network，RNN）是指在结构中加入了循环的概念，可以将时间维度上早先输入的信息应用到后续输出的计算过程中。

RNN在语音识别、自然语言处理、机器翻译等众多时序分析领域中取得了巨大的成就，
RNN与CNN并称为当下最热门的两大深度学习算法。

RNN能够更好的处理序列的信息，即前面的输入和后面的输入是有关系的。
很明显的例子：在语言处理中，一个句子前一个单词对当前的单词词性预测有很大影响，比如“吃苹果”，若前一个词是动词吃，那么苹果是名词的概率大于动词的概率。

RNN隐藏层相比常规网络多了时间维度的处理。

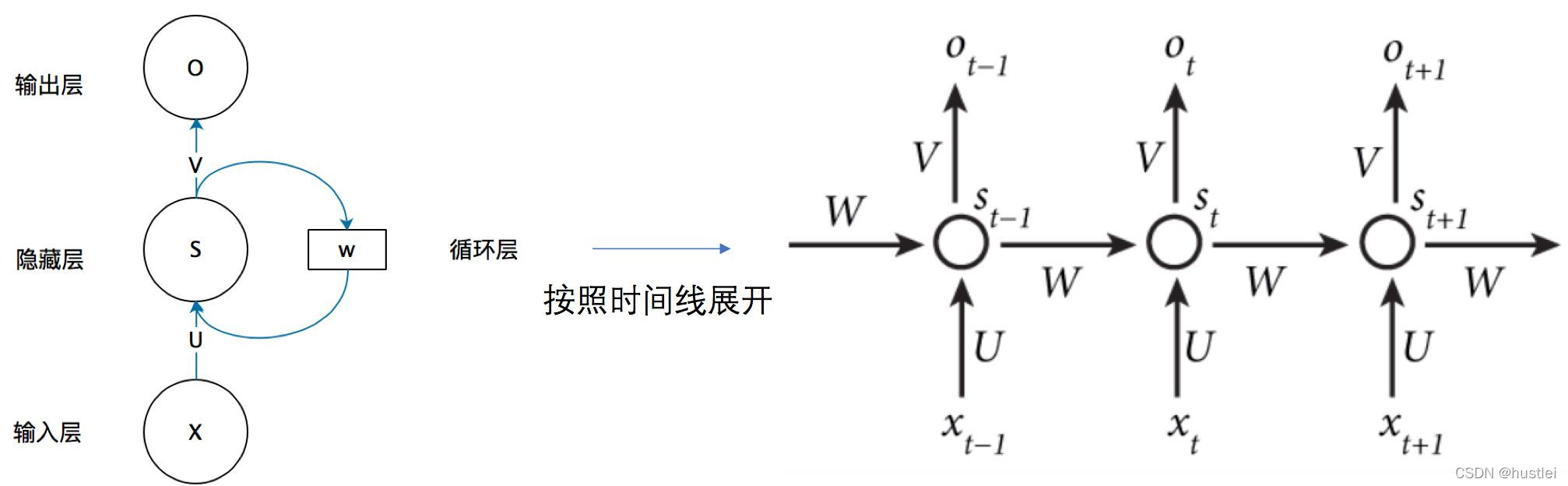
以下参数和常规网络相同：

• x是一个向量，它表示输入层的值（这里面没有画出来表示神经元节点的圆圈）；
• s是一个向量，它表示隐藏层的值（这里隐藏层面画了一个节点，你也可以想象这一层其实是多个节点，节点数与向量s的维度相同）；
• U是输入层到隐藏层的权重矩阵
• o也是一个向量，它表示输出层的值
• V是隐藏层到输出层的权重矩阵。

但是，W是RNN独有的，时间维度上的参数。
RNN的隐藏层的值s不仅仅取决于当前这次的输入x，还取决于上一次（时间维度）隐藏层的值s。权重矩阵W就是隐藏层上一次的值作为这一次的输入的权重。

即：

Ot=g(V*St)
St=f(U*Xt + W*St-1)`
1
2

5.3 长短时记忆神经网络LSTM简介

大量学者对基本RNN模型进行了改进，其中最成功的改进模型当属长短时记忆（LSTM）网络。
与普通的RNN相比，LSTM网络除了使用隐藏状态保存信息，还增加了记忆细胞，并设立了输入门、输出门和遗忘门来控制记忆细胞。

5.4 生成深度神经网络简介

生成模型（Generative Model）是指根据已知的样本训练模型，然后应用训练的模型生成一些新的样本，“生成”的样本和“真实”的样本尽可能地相似。

目前使用比较多的深度生成模型包括：

• 深度玻尔兹曼机（Deep Boltzmann Machine，DBM）
• 深度置信网络（Deep BeliefNetwork，DBN）
• 生成对抗网络（GenerativeAdversarial Network，GAN）
• 变分自编码器（Variational Autoencoder，VAE）

受限玻尔兹曼机(restricted Boltzmann machine, RBM)

受限玻尔兹曼机原理起源于统计物理学，是一种基于能量函数的建模方法。是一种可用随机神经网络（stochastic neural network）来解释的概率图模型。任何概率分布都可以转变成基于能量的模型，要寻找一个变量使得整个网络的能量最小，跟传统的神经网络类似，问题可转变成用梯度下降法求使能量函数（相当于BP算法里的损失函数P）值最小的权值和偏置，以使算法收敛到一个解（可能是局部最优解）。

受限玻兹曼机在降维、分类、协同过滤、特征学习和主题建模中得到了应用。
根据任务的不同，受限玻兹曼机可以使用监督学习或无监督学习的方法进行训练。

深度信念网络

受限玻兹曼机也可被用于深度学习网络。具体地，深度信念网络可使用多个RBM堆叠而成，并可使用梯度下降法和反向传播算法进行调优。

在深度生成模型中，更多的是对RBM进行堆叠，将RBM堆叠起来就得到了DBM；
如果加一个分类器，就得到了DBN。

生产对抗网络

深度学习模型可以分为判别式模型与生成式模型。

由于反向传播（Back propagation, BP）、Dropout等算法的发明，判别式模型得到了迅速发展。由于生成式模型建模较为困难，因此发展缓慢，直到近年来最成功的生成模型——生成式对抗网络的发明，这一领域才焕发新的生机。生成模型的任务是生成看起来自然真实的、和原始数据相似的实例。（真实实例来源于数据集，伪造实例来源于生成模型）

GAN有两个网络构成：G（Generator）和D（Discriminator）生成网络的目标就是尽量生成真实的图片去欺骗判别网络D。而网络D的目标就是尽量把网络G生成的图片和真实的图片分别开来。G和D构成了一个动态的“博弈过程”。

---

个人总结，部分内容进行了简单的处理和归纳，如有谬误，希望大家指出，持续修订更新中。

修订历史版本见：https://github.com/hustlei/AI_Learning_MindMap