数据结构之线性表和树_线性表存储树

1：线性表

具有同一数据类型的有限数据序列。线性表主要由顺序存储结构或链式存储结构（链表又包括单链表、循环链表、双向链表。）表示。在实际应用中，常以栈、队列、字符串等特殊形式使用。

在线性表中数据有前驱元素和后继元素（除第一个和最后一个元素外），每个元素都有自己的位置（简单理解为下标，可以通过get(i)获取）。
所以线性表结构的数据对于随机插入、删除、移动时间复杂度为O(n)。修改一条元素，元素其后面的元素都要改变位置。

• 顺序存储结构：具有连续的物理地址，数据连续在一起结构类似于数组。随机插入删除效率低。
• 链表存储结构：链表存储结构由指针（指向下个元素的物理存储地址）指向该元素的下个元素，查询的效率低，随机插入删除效率高·。

ArrayList 属于线性表的顺序存储结构。底层是数组。
LinkedList 是由链表实现的 插入删除效率高

1.1：栈和队列

栈和队列，严格意义上来说，也属于线性表。

• 使用栈结构存储数据，讲究“先进后出”，即最先进栈的数据，最后出栈；
• 使用队列存储数据，讲究 “先进先出”，即最先进队列的数据，也最先出队列。

1：栈

栈只能从表的一端存取数据，所以栈是先进后出的特性。
向栈中添加元素，此过程被称为"进栈"（入栈或压栈）；
从栈中提取出指定元素，此过程被称为"出栈"（或弹栈）

• 栈的开口端被称为栈顶；
• 相应地，封口端被称为栈底是封闭的，

栈的存储结构包括顺序栈和链栈

• 1：顺序栈：采用顺序存储结构可以模拟栈存储数据的特点，从而实现栈存储结构；
• 2：链栈：采用链式存储结构实现栈结构；

2：队列

队列的两端都"开口"，要求数据只能从一端进，从另一端出，所以特性是先进先出。医院挂号系统一般用队列存储。

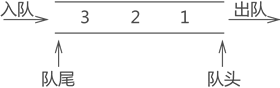
队列存储结构的实现有以下两种方式：

• 1：顺序队列：在顺序表的基础上实现的队列结构；
• 2：链队列：在链表的基础上实现的队列结构；

1.2：字符串

空串：存储 0 个字符的串，例如 S = “”（双引号紧挨着）；
空格串：只包含空格字符的串，例如 S = " "（双引号包含 5 个空格）。
需要注意的是，空格串和空串不同，空格串中含有字符，只是都是空格而已。

2：树存储结构

图 1(A) 是使用树结构存储的集合 {A,B,C,D,E,F,G,H,I,J,K,L,M} 的示意图。对于数据 A 来说，和数据 B、C、D 有关系；对于数据 B 来说，和 E、F 有关系。这就是“一对多”的关系。

1：树的结点

• 结点：使用树结构存储的每一个数据元素都被称为“结点”。例如，图中，数据元素 A
• 父结点（双亲结点）、子结点和兄弟结点：对于图 中的结点 A、B、C、D 来说，A 是 B、C、D 结点的父结点（也称为“双亲结点”），而 B、C、D 都是 A 结点的子结点（也称“孩子结点”）。对于 B、C、D 来说，它们都有相同的父结点，所以它们互为兄弟结点。
• 树根结点（简称“根结点”）：每一个非空树都有且只有一个被称为根的结点。图中，结点 A 就是整棵树的根结点。
  树根的判断依据为：如果一个结点没有父结点，那么这个结点就是整棵树的根结点。
• 叶子结点：如果结点没有任何子结点，那么此结点称为叶子结点（叶结点）。例如图 中，结点 K、L、F、G、M、I、J 都是这棵树的叶子结点。

特征1：基本所有的树都要遵循左小右大原则

2.1：二叉树

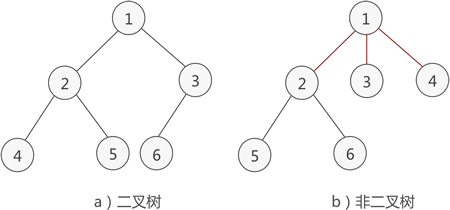
简单地理解，满足以下两个条件的树就是二叉树：

• 本身是有序树；（1-6从上到下，从左到右依次从小到大）
• 树中包含的各个节点的度（分支）不能超过 2，即只能是 0、1 或者 2

1：二叉树的特性
经过前人的总结，二叉树具有以下几个性质：

• 二叉树中，第 i 层最多有 2(i-1)次方个结点。比如第二层=2*（2-1）次方
• 如果二叉树的深度为 K（最大层数），那么此二叉树最多有 2K（2的k次方）-1 个结点。
  二叉树中，终端结点数（叶子结点数）为 n0，度为 2 的结点数为 n2，则 n0=n2+1。
• 二叉树的右边节点一定比左边值大（有序）
• 节点数=分支数+1。分支数就是连接节点的线条个数。

1：二叉树的存储结构

二叉树的存储结构的分为顺序存储和链式存储
顺序存储：所有节点按照层次顺序存储到数组中（只适用于完全二叉树）

顺序存储为下图

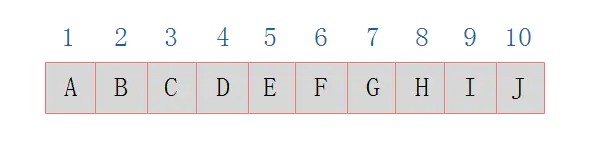
链式存储：从根节点开始所有节点都使用链表存储（左-数据-右）

2：二叉树的遍历

二叉树的遍历是指从二叉树的根结点出发，按照某种次序依次访问二叉树中的所有结点，使得每个结点被访问一次，且仅被访问一次。

二叉树的访问次序可以分为四种：

• 1：前序遍历：通俗的说就是从二叉树的根结点出发，当第一次到达结点时就输出结点数据，按照先向左在向右的方向访问。
  输出ABDHIEJCFG
• 2：中序遍历：中序遍历就是从二叉树的根结点出发，当第二次到达结点时就输出结点数据，按照先向左在向右的方向访问。
  输出HDIBJEAFCG
• 3：后序遍历
• 4：层序遍历

3：二叉查找树

二分法是我们常用的一种查找算法，可以有效的提升数据找找的效率，其实现思路是：

• 1、首先对数据集进行排序。

• 2、找到数据集中间位置的节点。

• 3、用查找的条件和间节点进行比较，等于则直接返回，中间节点数据小于查找条件则说明数据在排序列表的左边，大于则说明数据在排序列表的右边。

二叉树就是充分利用了二分查找法的思维。
二分查找树特性：

• （1）若左子树不空，则左子树上所有节点的值均小于它的根节点的值；
• （2）若右子树不空，则右子树上所有节点的值均大于它的根节点的值；
• （3）左、右子树也分别为二叉搜索树；

根据二叉搜索树左右子树的有序特性了可以有效提高查找效率。
二叉搜索树的查找效率取决于树的高度。
链表形式的左斜树或者右斜树查找复杂度为O(n)。
满二叉树的效率最高为O(logn)

4：平衡二叉树

左右子树的高度相差不超过1的树为平衡二叉树。
平衡因子：某节点的左子树与右子树的高度(深度)差即为该节点的平衡因子（BF,Balance Factor），平衡二叉树中不存在平衡因子大于1的节点。在一棵平衡二叉树中，节点的平衡因子只能取-1、1或者0。

在插入二叉树时，如果二叉树的平衡因子不是-1、1、0，则需要进行左旋或者右旋改变树的深度，使得平衡因子符合要求。

2.2：红黑树（面试重点）

红黑树是一种独特的二叉树。
红黑树是每个结点都带有颜色属性的二叉查找树，颜色或红色或黑色。
在二叉查找树强制一般要求以外，对于任何有效的红黑树我们增加了如下的额外要求:
性质1. 结点是红色或黑色。
性质2. 根结点是黑色。
性质3. 所有叶子都是黑色。（叶子是NIL结点）
性质4. 每个红色结点的两个子结点都是黑色。（从每个叶子到根的所有路径上不能有两个连续的红色结点）
性质5. 从任一节结点到其每个叶子的所有路径都包含相同数目的黑色结点。

二叉树的应用：Java的容器TreeSet、TreeMap均使用红黑树实现。JDK1.8中HashMap中也加入了红黑树。
让红黑树达到平衡状态，主要包括染色、↔左右旋转。
红黑树的查找操作与二叉搜索树查找方式一致，插入时违反5大性质的情况要进行左旋或者右旋。

2.3：2-3树

2-3树本质也是一种平衡搜索树，但2-3树已经不是一棵二叉树了，因为2-3树允许存在3这种节点，3-节点中可以存放两个元素，并且可以有三个子节点。

性质：
（1）对于每一个结点有1或者2个关键码（关键码：几对Key-Value值）。
（2）当节点有1个关键码的时，节点有2个子树。
（3）当节点有2个关键码时，节点有3个子树。
（4）所有叶子点都在树的同一层。

2.3：B树

它是一颗多路平衡查找树。，一般用字母m表示阶数。当m取2时，就是我们常见的二叉搜索树，m为3时是2-3树。

（1）每个结点最多有m-1个关键字。
（2）根结点最少可以只有1个关键字。
（3）非根结点至少有Math.ceil(m/2)-1个关键字。Math.ceil(m/2)含义是向上取整。
	例如Math.ceil(4.5) = 5。
（4）每个结点中的关键字都按照从小到大的顺序排列，每个关键字的左子树中的所有关键字都小于它，
	而右子树中的所有关键字都大于它。
（5）所有叶子结点都位于同一层，或者说根结点到每个叶子结点的长度都相同。
1
2
3
4
5
6
7

关键字的范围：

• 根节点的关键字数量范围：1 <= k <= m-1
• 非根节点的关键字数量范围：m/2 <= k <= m-1。

1： B树插入

插入的时候，我们需要记住一个规则：判断当前结点key的个数是否小于等于m-1，如果满足，直接插入即可，如果不满足，将节点的中间的key将这个节点分为左右两部分，中间的节点放到父节点中即可。

例子：在5阶B树中，结点最多有4个key,最少有2个key（注意：下面的节点统一用一个节点表示key和value）。

插入18，70，50,40

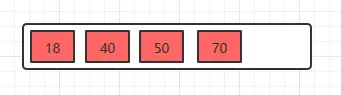
插入22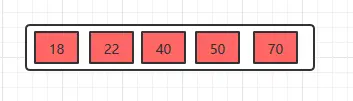
插入22时，发现这个节点的关键字已经大于4了，所以需要进行分裂，分裂的规则在上面已经讲了，分裂之后，如下。

接着插入23，25，39

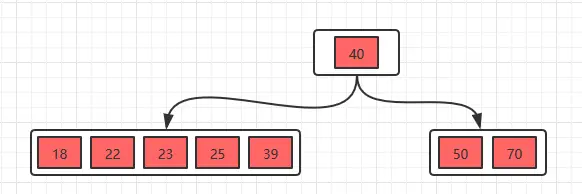
4：B+树

B+树是在B树基础进一步优化得到的一种数据结构。B+树相比于B树具有更高的查询效率。

B+树定义：

（1）B+树包含2种类型的结点：内部结点（也称索引结点）和叶子结点。
（2）根结点本身即可以是内部结点，也可以是叶子结点。根结点的关键字个数最少可以只有1个。
（3）B+树与B树最大的不同是内部结点不保存数据，只用于索引，所有数据（或者说记录）都保存在叶子结点中。
（4） m阶B+树表示了内部结点最多有m-1个关键字（或者说内部结点最多有m个子树），阶数m同时限制了叶子结点最多存储m-1个数据。
（5）内部结点中的key都按照从小到大的顺序排列，对于内部结点中的一个key，左树中的所有key都小于它，右子树中的key都大于等于它。叶子结点中的数据也按照key的大小排列。
（6）每个叶子结点都存有相邻叶子结点的指针，叶子结点本身依关键字的大小自小而大顺序链接。

3：各种查询算法

3.1：二分查找法

使用于有序表，每次使用前必须保证查找特征的有序性。