动态规划- 股票问题专题（详解+多例子+源码）_股票动态规划

动态规划做题思路

像这种股票问题，我们首先想多状态动态规划 ，先分析

① 状态表示： dp[ i ]表示什么

我们这里用的是多状态，所以不用dp命名，用f[ i ]和 g[ i ]命名

一般我们 用 f[ i ]表示第 i 天当前手中持有股票的最大收益

               用g[ i ]表示第 i 天当前手中未持有股票的最大收益

当然如果有其他的情况要分析是否需要其他状态 需要具体分析

②状态转移方程

因为我们用的是多状态，所以我们要分析没个状态是否可以由其他状态得到 怎么得到的，或者由自己得到，一定要分析全面 

状态转移要根据状态表示来推导，我们状态表示是最大收益，就要将可以转移到该状态的所有情况取最大值，填入到当前值中 如果有其他状态表示 根据具体分析即可

买股票的最佳时机含冷冻期 (medium)

首先先解释题目：我们可以进行多次交易，但是当我们卖出股票的时候，我们会被冷冻一天，这一天中不能进行买股票行为

 

 像这种买股票的问题，我们可以用多状态动态规划来解决（直接秒杀）需要分析

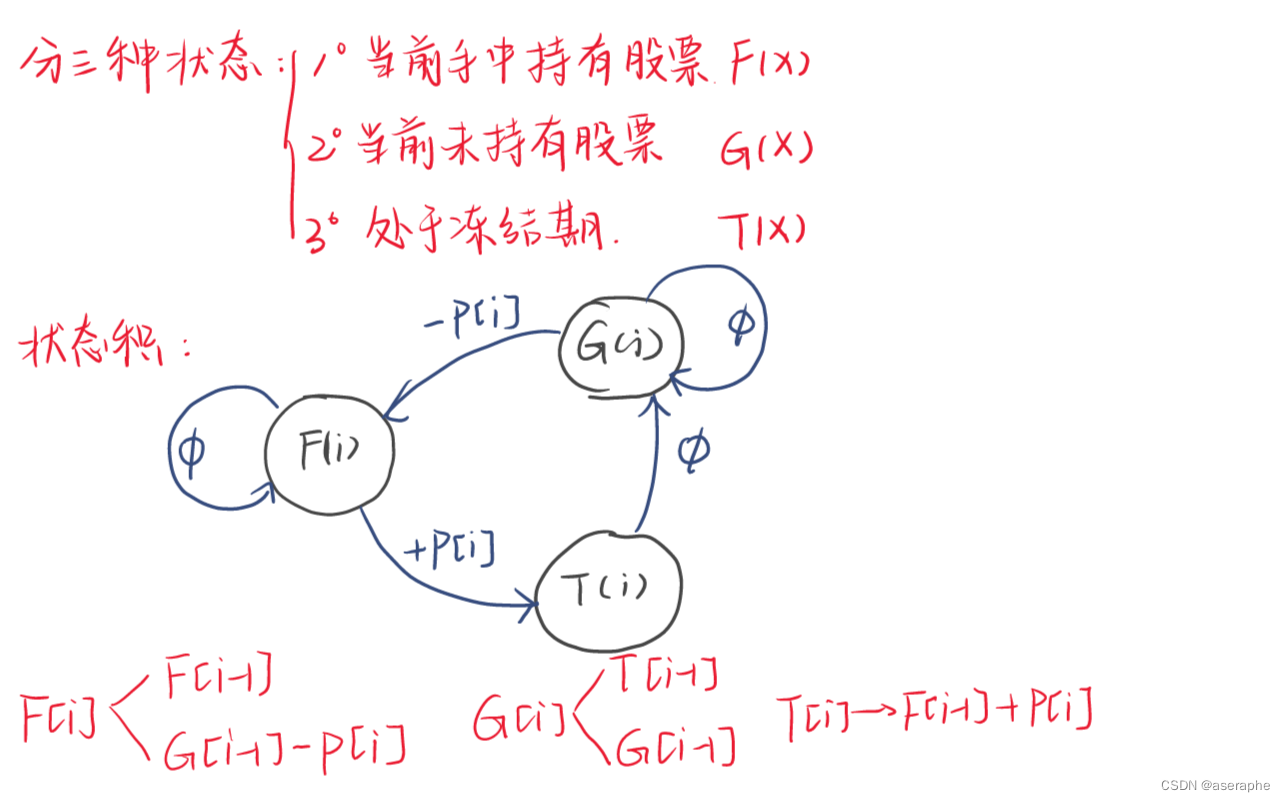
如上图 ：因为含冷冻期，我们把冷冻期的状态也加上，具体分析画出状态积 

F可以从未持有股票进行一次购买转移得到，也可以由自己无需操作得到

G可以从冷冻期第二天解冻得到，也可以有自己无需操作的到

T只可以从上一天卖出股票转换得到

分析出了每种状态的转移方程，只需要对每种状态取最大值即可

class Solution {
public:
    int maxProfit(vector<int>& prices) {
        int n=prices.size();
 
        vector<vector<int>>dp(n,vector<int>(3));
        dp[0][0]=-prices[0];
        dp[0][1]=dp[0][2]=0;
        //dp[i][0]当前状态是买入
        //dp[i][1]当前状态是可交易
        //dp[i][2]当前状态被冻结
 
        for(int i=1;i<n;i++)
        {
            dp[i][0]=max(dp[i-1][0],dp[i-1][1]-prices[i]);
            dp[i][1]=max(dp[i-1][1],dp[i-1][2]);
            dp[i][2]=dp[i-1][0]+prices[i];
        }
        return max(max(dp[n-1][0],dp[n-1][1]),dp[n-1][2]);
    }
};

 

 买股票的最佳时机含手续费（medium）

解释题目：这次不含冷冻期，但是每次交易需要付手续费，还是可以多次交易 。首先我们要明确一次交易，我们可以在买入的时候付手续费，卖出的时候就不需要再付，或者买入的时候不付，卖出的时候付手续费，这里我们都以卖出的时候付手续费

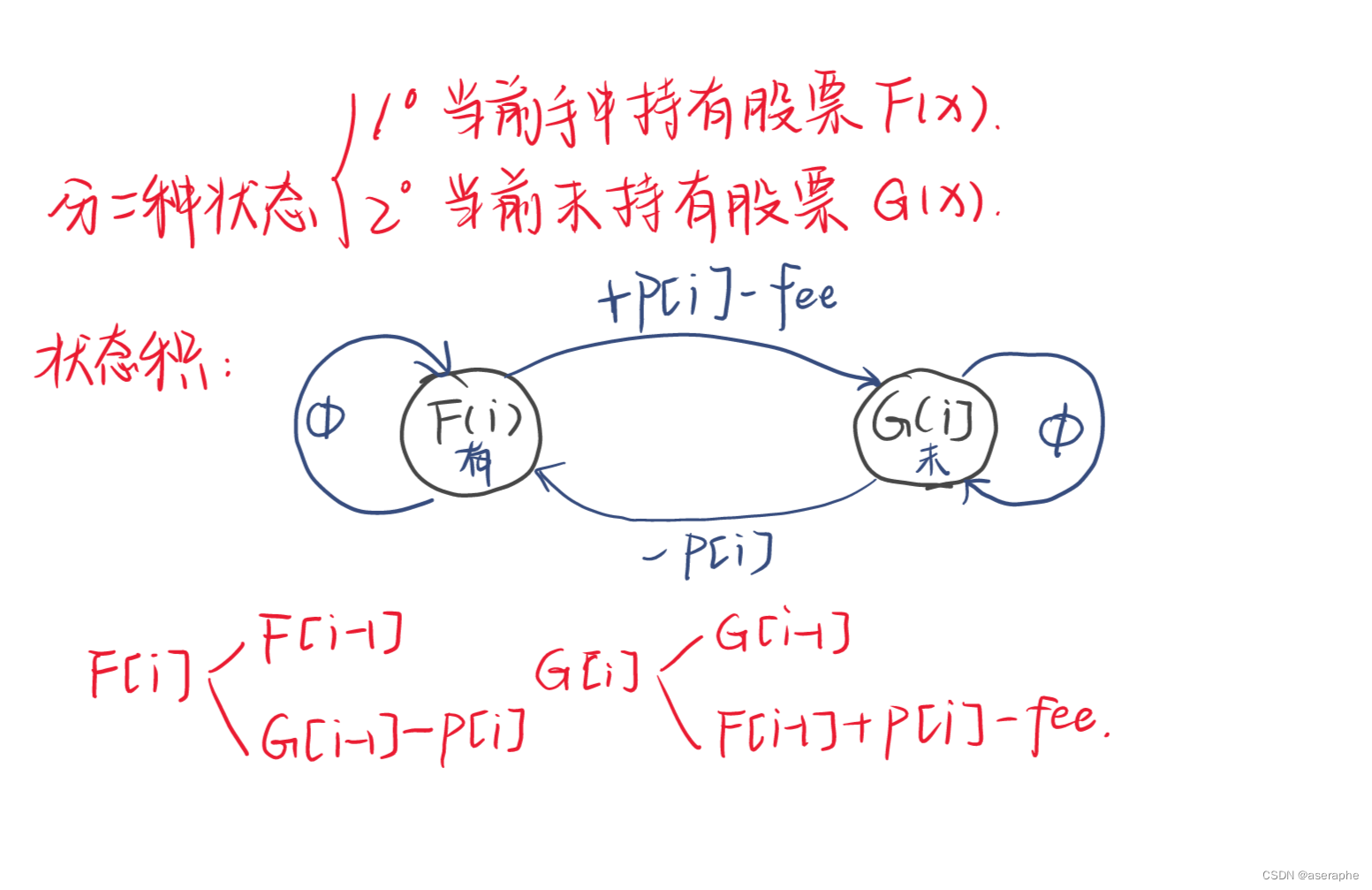
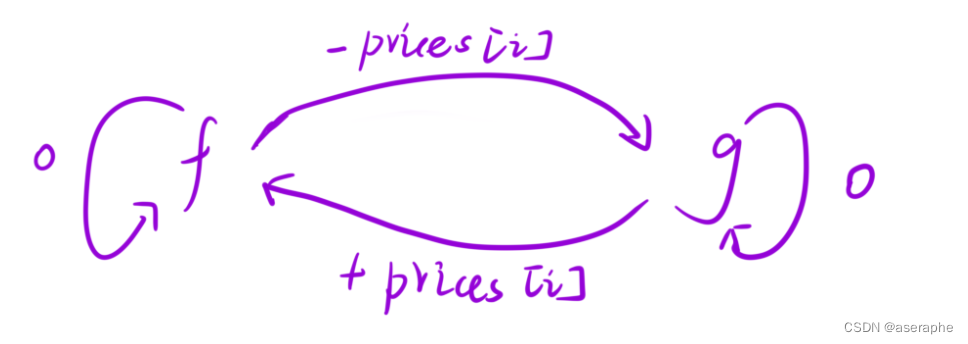
还是先分状态，这题只需要分两种状态，直接画出状态积，分析每种状态如何转化：

F（持有）可以由上一天的持有状态，什么都不做转化来，也可以上天手中未持有股票，通过买入操作转化来

G（未持有）可以由上一天未持有 什么都不做转化来，还可以上一天手中持有股票，进行卖出操作（同时需要付手续费）转化来

所以状态转移方程就的到了

class Solution {
public:
    int maxProfit(vector<int>& prices, int fee) {
        int n = prices.size();
        vector<int> f(n);
        auto g = f;
        f[0] = -prices[0];
        for (int i = 1; i < n; i++) {
            f[i] = max(f[i - 1], g[i - 1] - prices[i]);
            g[i] = max(g[i - 1], f[i - 1] + prices[i] - fee);
        }
        return g[n - 1];
    }
};

 买股票的最佳时机Ⅲ（hard）

这道题没有手续费，没有冷冻期，但是只可以进行两次交易，我们还是需要明确一次交易的概念，只可以进行两次买  卖

 

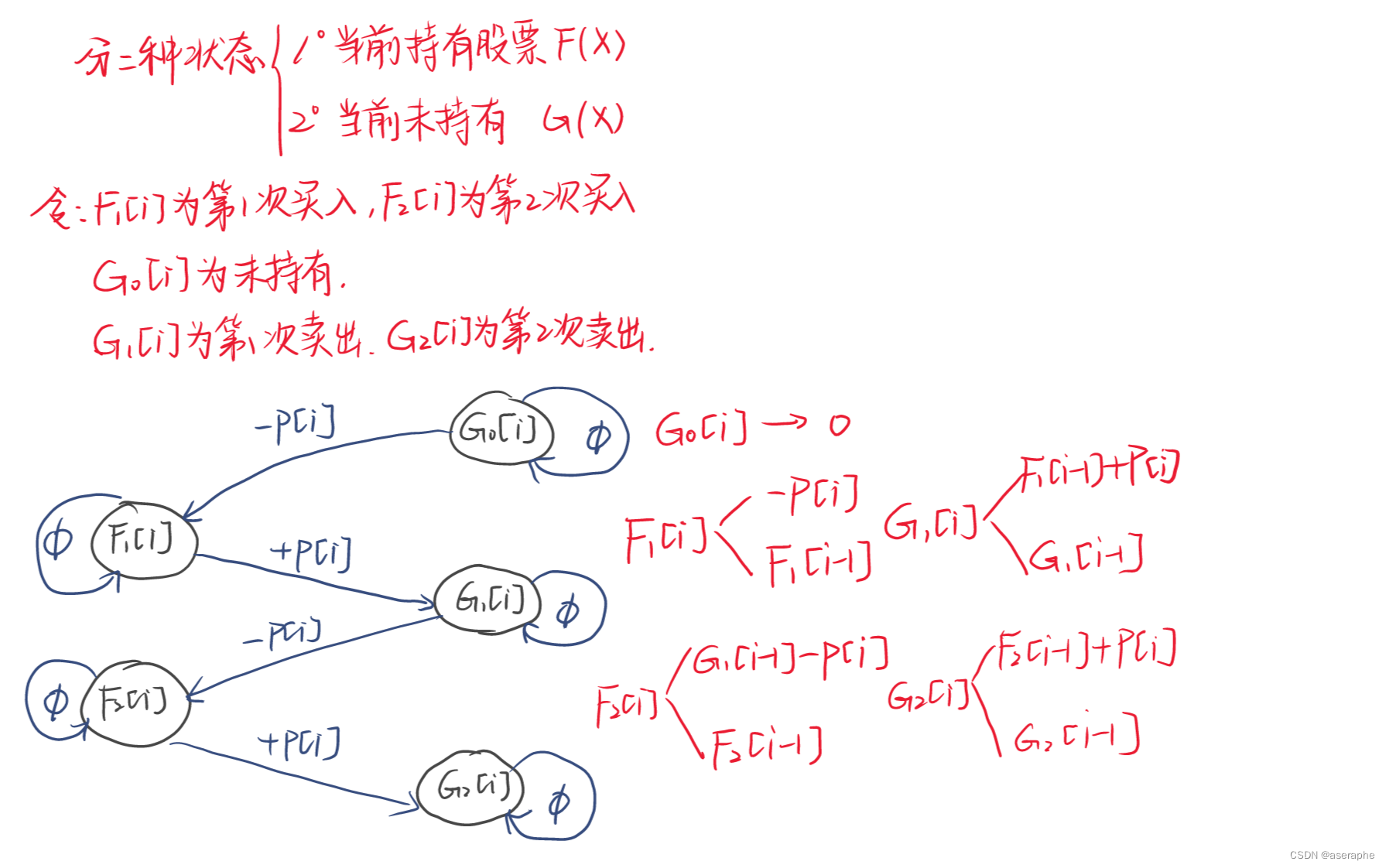
这次我们需要定义五个状态，每个状态表示如图，我们只需要模拟这两次购买 即可的到状态积，很容易分析出状态转移方程，其中G0一直都是0 因为我们一直没有进行购买操作，手中什么都没有。 

class Solution {
public:
    int maxProfit(vector<int>& prices) {
        int n=prices.size();
        vector<int>G0(n);
        vector<int>G1(n);
        vector<int>G2(n);
        vector<int>F1(n);
        vector<int>F2(n);
        F1[0]=-prices[0];
        F2[0]=-prices[0];
        //从第二个元素开始填
        
        for(int i=1;i<n;i++)
        {
            F1[i]=max(G0[i-1]-prices[i],F1[i-1]);
            G1[i]=max(F1[i-1]+prices[i],G1[i-1]);
            F2[i]=max(G1[i-1]-prices[i],F2[i-1]);
            G2[i]=max(F2[i-1]+prices[i],G2[i-1]);
        }
        return G2[n-1];
    }
};

 买股票的最佳时机Ⅳ（hard）

类比上一道题：

在我们上一道题填表的时候 ：

可以看到十分的有规律，上道题只能交易两次，但是这道题只能交易k次，所以两道题几乎一样

class Solution {
public:
    int maxProfit(int k, vector<int>& prices) {
        const int INF = 0x3f3f3f3f;
        // 处理⼀个细节问题
        int n = prices.size();
        k = min(k, n / 2);
        // 创建 dp 表
        // 初始化
        // 填表
        // 返回值
        vector<vector<int>> f(n, vector<int>(k + 1, -INF));
        auto g = f;
        f[0][0] = -prices[0], g[0][0] = 0;
        for (int i = 1; i < n; i++) {
            for (int j = 0; j <= k; j++) {
                f[i][j] = max(f[i - 1][j], g[i - 1][j] - prices[i]);
                g[i][j] = g[i - 1][j];
                if (j >= 1) // 如果状态存在
                    g[i][j] = max(g[i][j], f[i - 1][j - 1] + prices[i]);
            }
        }
        int ret = 0;
        for (int j = 0; j <= k; j++)
            ret = max(ret, g[n - 1][j]);
        return ret;
    }
};