链表经典OJ问题【环形链表】

题目导入

题目一：给你一个链表的头节点 head ，判断链表中是否有环
题目二：给定一个链表的头节点 head ，返回链表开始入环的第一个节点。 如果链表无环，则返回 NULL。

题目一

给你一个链表的头节点 head ，判断链表中是否有环。
如果链表中有某个节点，可以通过连续跟踪 next 指针再次到达，则链表中存在环。 为了表示给定链表中的环，评测系统内部使用整数 pos 来表示链表尾连接到链表中的位置（索引从 0 开始）。注意：pos 不作为参数进行传递 。仅仅是为了标识链表的实际情况。
如果链表中存在环 ，则返回 true 。 否则，返回 false 。

分析

这里我们不能用单个指针来判断是否带环，这样是行不通的，因为我们不知道结束条件是什么；可能有人会想“让单个指针与带环链表的入口进行对比”，但是这有个问题，我们并不知道哪个节点是这个环形链表的节点。
类似下图

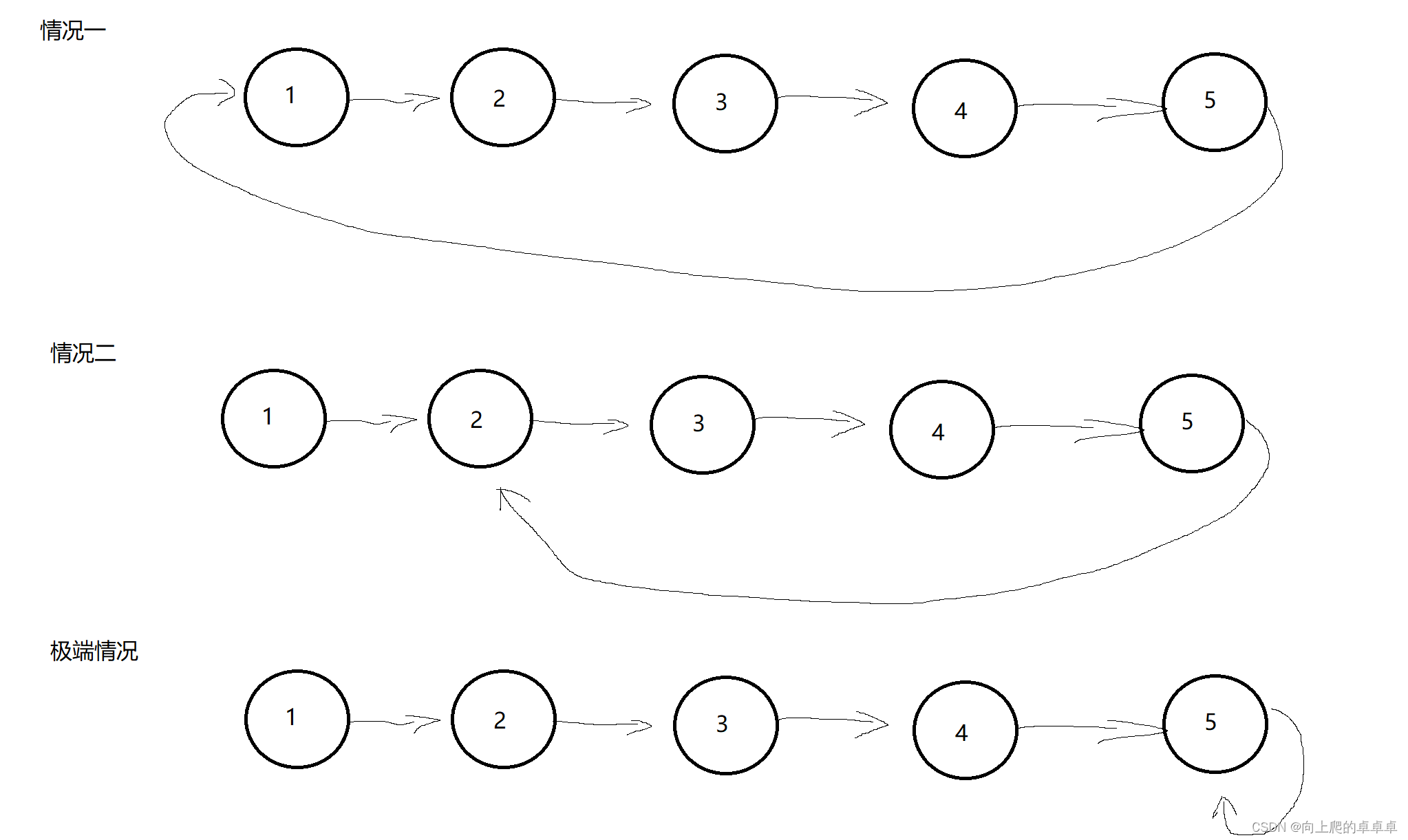
尾节点的next指向哪里是不确定的，有可能指向头节点，也有可能指向其他节点(极端情况指向自己)，还有可能就不是一个环形链表(指向NULL)。

所以这里要使用快慢指针(这是一个很棒的解题思路)，在这个题我们就让慢指针走一步，快指针走两步。
具体代码如下

struct ListNode* slow = head , *fast = head;
slow = slow->next;//慢指针走一步
fast = fast->next->next;//快指针走两步
1
2
3

这个指针不可能只会走一次的，所以是需要循环来完成的

bool hasCycle(struct ListNode *head) {
    struct ListNode* slow = head , *fast = head;
    while()
    {
        slow = slow->next;
        fast = fast->next->next;
    }
    return false;//链表不为环形链表
    
}
1
2
3
4
5
6
7
8
9
10

这里的结束条件是什么呢？
这里是判断该链表是否为环形链表，所以我们的判断条件是fast != NULL && fast->next != NULL。
这里为什么要判断fast->next呢，假设这条链表不是环形链表，且fast->next是指向NULL，如果我们不对 fast->next进行判断的话，进入循环就会出现fast->next已经为空，我们还对他进行了解引用，这样就会报错
所以这里的结束条件为

while(fast && fast->next)
{
	…………//代码段
}
1
2
3
4

好了，循环已经写好了，那么来写结束条件吧(判断是否带环)，不能说因为代码死循环了就说链表是环形链表吧。
当slow等于fast时就表示该链表为环形链表。
为什么呢？
我们借图来了解：

开始将head赋予给slow和fast
因为fast指针的行走速度是slow指针的两倍，所以当slow走了链表的中间节点时，fast就已经走到尾节点了。

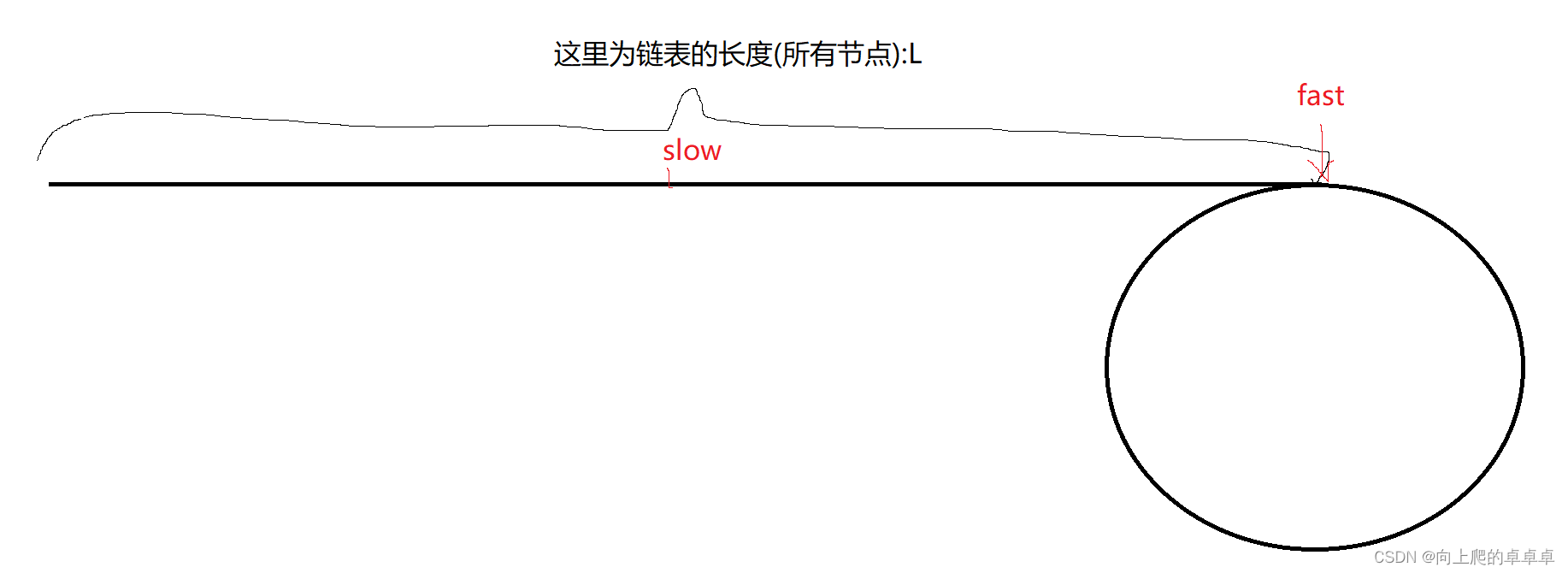
当slow走到尾节点时，就代表slow也进环了，这时候就成了追击问题，当fast == slow时，就代表该链表是环形链表。
完整代码如下：

bool hasCycle(struct ListNode *head) {
    struct ListNode* slow = head , *fast = head;
    while(fast && fast->next)
    {
        slow = slow->next;
        fast = fast->next->next;
        if(slow == fast)//相等，代表为环形链表
        {
            return true;
        }
    }
    return false;//不是环形链表
}
1
2
3
4
5
6
7
8
9
10
11
12
13

题目衍生问题

1. 为什么一定为相遇，难道不会错过了，再也无法相遇呢？
2. 如果我的fast走的不是两步，而是三步，四步或者更多呢？

衍生问题一

要证明这个很简单。
当slow走到尾节点时，就代表slow也进环了，但这时候的fast的位置是不确定(可能已经转了好多圈了)，所以我们假设fast和slow的距离为N
如图：

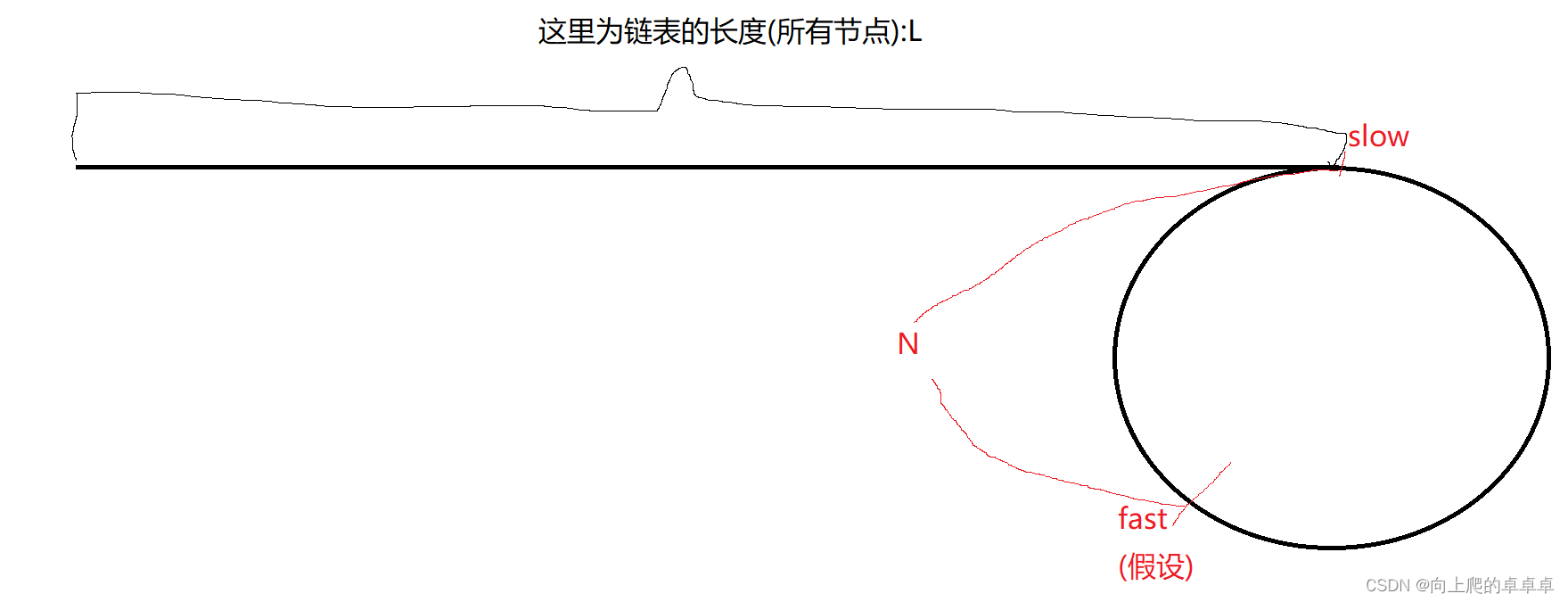
因为fast是slow的两倍，所以追击一次，他俩之间的距离就会减一，一直追击下去距离就会一直减一，直到为0，也就是他两相等了

距离：N -> N-1 -> N-2 -> ……-> 2 -> 1 -> 0

因为fast是slow的两倍，所以每追击一次，他们的距离就会减一，所以他们两个不会错过。

衍生问题二

我们拿fast一次走三步来举例(其他的证明过程都大差不多，无非就是更复杂了)。
这时fast的速度就是slow的三倍，这时每追击一次，距离就会减二，这时候就要考虑两个情况了

• 情况一：他们两个之间的距离为偶数
  这很简单，因为N为偶数，所以N%2=0；所以他们一定会在第一轮相遇。
• 情况二：距离为奇数
  这样追击下去，当他们之间的距离为1时，在追击一次后，fast就会跑到slow的前面，开启新一轮的追击

N为奇数： N -> N-2 -> N-4 -> …… -> 5 -> 3 -> 1 -> -1

假设这个环形链表的长度为C。
这时候又要看两种情况这个C-1是否为偶数；
当C-1为偶数时，那么就和情况一一样，就一定会相遇。
如果C-1还是奇数，那就真的永远都遇不到了。

那么真的会出现N为奇数，C为偶数(C-1为奇)的情况吗？
其实是不可能的，我们将他们进行换算就可以知道为什么了。

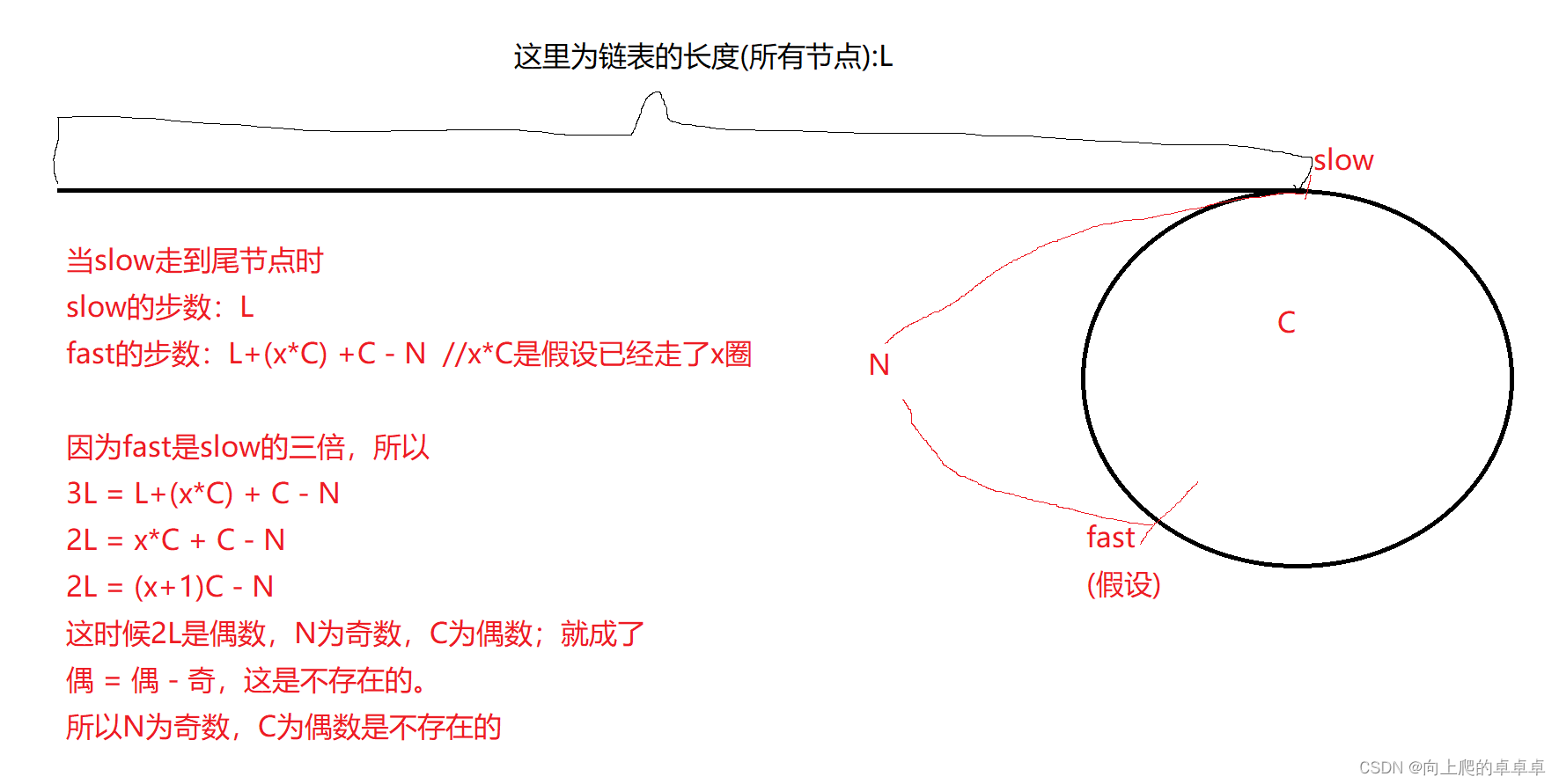
总结论：使用快慢指针，环形链表一定会相遇，如果N为偶数，那么C一定为偶数；N为奇数，C一定为奇数。

题目二

给定一个链表的头节点 head ，返回链表开始入环的第一个节点。 如果链表无环，则返回 null。
如果链表中有某个节点，可以通过连续跟踪 next 指针再次到达，则链表中存在环。 为了表示给定链表中的环，评测系统内部使用整数 pos 来表示链表尾连接到链表中的位置（索引从 0 开始）。如果 pos 是 -1，则在该链表中没有环。注意：pos 不作为参数进行传递，仅仅是为了标识链表的实际情况。
不允许修改 链表。

这里就是在判断环形链表的基础上再加一些要求，那前置的代码，可以直接使用上面的代码

struct ListNode *detectCycle(struct ListNode *head) {
    struct ListNode* slow = head , *fast = head;
    while(fast && fast->next)
    {
        slow = slow->next;
        fast = fast->next->next;
        if(slow == fast)//相遇了
        {
			
        }
    }
    return NULL;//无环
}
1
2
3
4
5
6
7
8
9
10
11
12
13

那既让相遇了，我们肯定就是在相遇之后进行操作，也就是在if语句里写代码。
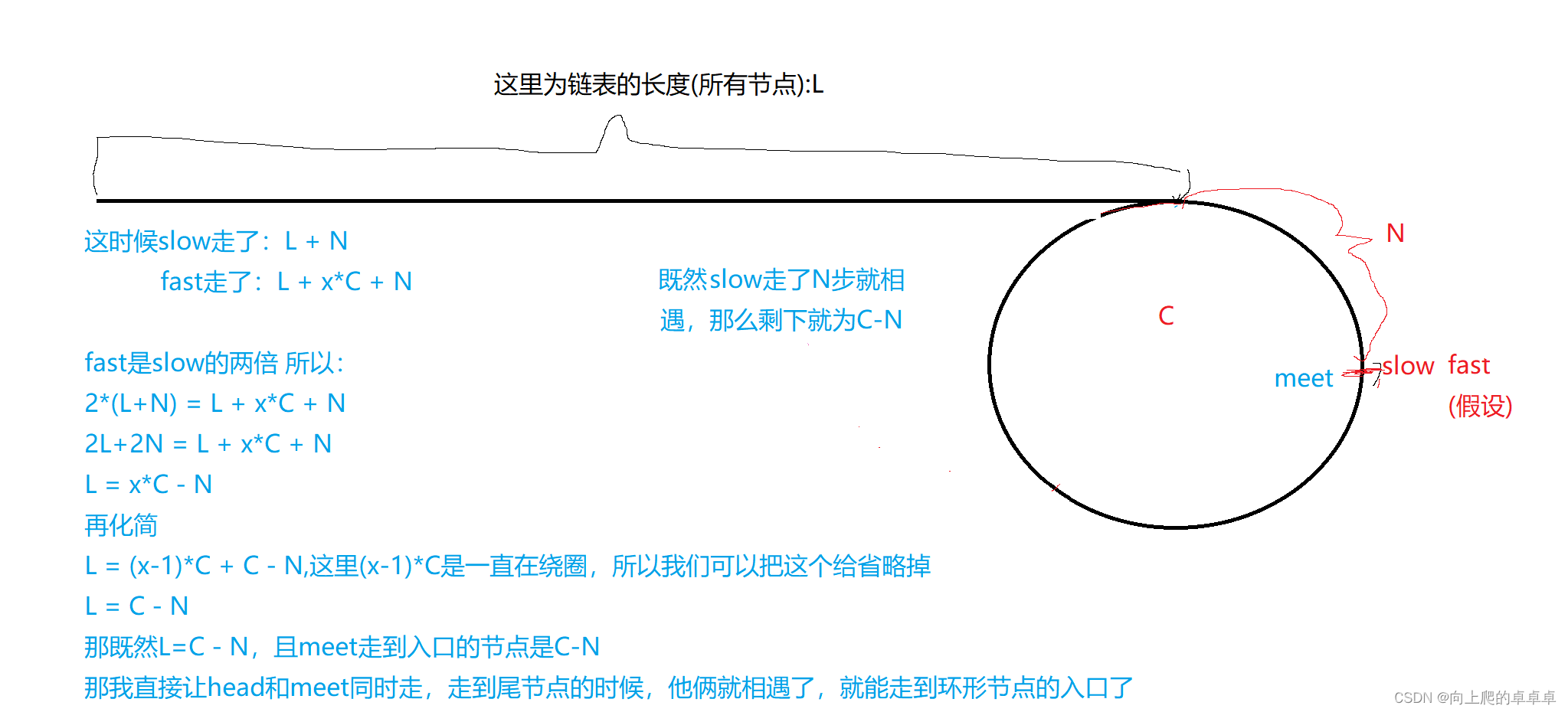
既让已经相遇了，那么slow的步数就为L+N(slow在环内走了 N 步)，fast的步数就为L + x*C + N(走了一圈x就加1，然后因为slow在环内走了 N 步，使用就为x*C+N)。
我们将slow 与 fast相遇时的节点，给到meet

        if(slow == fast)//相遇了
        {
			struct ListNode* meet = slow;//这里给fast也行
        }
1
2
3
4

我们看图来进行换算：

完整代码：

struct ListNode *detectCycle(struct ListNode *head) {
    struct ListNode* slow = head , *fast = head;
    while(fast && fast->next)
    {
        slow = slow->next;
        fast = fast->next->next;
        if(slow == fast)
        {
            struct ListNode* meet = slow;
            while(meet != head)//同时走
            {
                meet = meet->next;
                head = head->next;
            }
            return meet;//走到这里就代表meet == head
        }
    }
    return NULL;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19

其实这两题本意都不难，难的是衍生问题和背后的数学逻辑(其实拆开了也不难)，所以这也成了以前面试时会考的点，
考察的是你的逻辑思维。

结语

最后感谢您能阅读完此片文章，如果有任何建议或纠正欢迎在评论区留言，也可以前往我的主页看更多好文哦(点击此处跳转到主页)。
如果您认为这篇文章对您有所收获，点一个小小的赞就是我创作的巨大动力，谢谢！！！