- 1deep Q-network (DQN)_deep q-network经典论文
- 2Java在线外卖订餐系统设计与实现(Idea+Springboot+mysql)_外卖小程序系统开发idea
- 3OpenHarmony适配开源图形驱动(旧框架)--RK3568_panfrost
- 4《Kali渗透基础》15. WEB 渗透_kali web渗透
- 5【Spring boot实战】Springboot+对话ai模型整体框架+高并发线程机制处理优化+提示词工程效果展示(按照框架自己修改可对接市面上百分之99的模型)_springboot ai
- 6最新技术解析:Open ai新推出了视频生成工具Sora_open暧暧的视频生成软件
- 7蓝桥杯——左移右移_c语言蓝桥杯算法训练 移动
- 8android setrotation 镜像,android - How to fit TextureView to screen after setRotation() - Stack Overfl...
- 9SE-Net网络详解
- 10考计算机一级应该学什么条件,计算机一级考试要求
Kaggle实战入门(一)之泰坦尼克号_泰坦尼克号kaggle
赞
踩
博主最近开始在Kaggle上做项目,第一个项目就是最经典的项目泰坦尼克号。在尝试了几种模型,调整了很多次之后,终于将模型调到0.8的得分,给大家分享一下我的做法。

Part1.数据导入和初步观察
导入泰坦尼克号训练集和测试集的数据,这次我选择同时处理两份数据,所以直接将他们拼接起来
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
import warnings
warnings.filterwarnings('ignore')
train=pd.read_csv('train.csv')
test=pd.read_csv('test.csv')
datas = pd.concat([train, test], ignore_index = True)
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
我们来看一下数据的组成
train.head()
- 1

可以看到我们的数据集有12个特征,每个特征的重要程度和作用:
| 特征 | 作用和重要程度 |
|---|---|
| 乘客ID | 索引 |
| 是否生存 | 0代表死亡,1代表存活 |
| 社会等级 | 分为1,2,3等级 |
| 姓名 | 重要,可以提炼出大量有用的信息 |
| 性别 | 重要 |
| 年龄 | 重要 |
| 直系亲友 | 一般,和旁系亲友共同处理 |
| 旁系亲友 | 一般,和直系亲友共同处理 |
| 票号 | 一般 |
| 票价 | 重要 |
| 舱门编号 | 一般 |
| 上船时的港口编号 | 一般 |
查看我们的数据集的缺失情况
train.info()
- 1

可以看到我们的特征还是比较完整的,只有三个特征有缺失的情况,分别是年龄,舱门编号和上船时的港口编号。其中年龄和舱门编号缺失的值比较多,待会需要特殊处理一下。
Part2.数据分析和特征工程
1、数据分析
(1)死亡与存活的比例
train['Survived'].value_counts()
- 1

(2)社会等级对存活的影响:社会等级越高,存活率越高
sns.barplot(x="Pclass", y="Survived", data=datas)
- 1

(3)性别对存活的影响:女性的存活率远大于男性
sns.barplot(x="Sex", y="Survived", data=datas)
- 1

(4)年龄对存活的影响:在0~35岁中的人群具有更高的生存概率,高于35岁的人群生存概率较低
facet = sns.FacetGrid(datas, hue="Survived",aspect=2)
facet.map(sns.kdeplot,'Age',shade= True)
facet.set(xlim=(0, train['Age'].max()))
facet.add_legend()
plt.xlabel('Age')
plt.ylabel('Survived')
- 1
- 2
- 3
- 4
- 5
- 6

(5)亲属对存活的影响:拥有2~4位家庭成员的人存活率更高
sns.barplot(x="SibSp", y="Survived", data=datas)
- 1

sns.barplot(x="Parch", y="Survived", data=datas)
- 1

将直系和旁系亲属两个特征合并为家庭大小,可以让我们更直观地观察亲属这个特征对存活率的影响
datas['FamilySize']=datas['SibSp']+datas['Parch']+1
sns.barplot(x="FamilySize", y="Survived", data=datas)
- 1
- 2

(6)登船时港口的不同对存活的影响:C和Q地的存活率更高,S地的存活率较低
sns.countplot('Embarked',hue='Survived',data=datas)
- 1

2、特征工程
(1)名字的处理
在数据分析中我们可以看到,社会等级对我们的存活率影响非常明显,所以我们可以将姓名替换为称呼前缀,生成新的特征‘Title’,用来对应我们的社会等级。这样我们就将一大串看似没有用的姓名特征转化成了有用的分类型特征。
datas['Title'] = datas['Name'].apply(lambda x:x.split(',')[1].split('.')[0].strip())
datas['Title'].replace(['Capt', 'Col', 'Major', 'Dr', 'Rev'],'Officer', inplace=True)
datas['Title'].replace(['Don', 'Sir', 'the Countess', 'Dona', 'Lady'], 'Royalty', inplace=True)
datas['Title'].replace(['Mme', 'Ms', 'Mrs'],'Mrs', inplace=True)
datas['Title'].replace(['Mlle', 'Miss'], 'Miss', inplace=True)
datas['Title'].replace(['Master','Jonkheer'],'Master', inplace=True)
datas['Title'].replace(['Mr'], 'Mr', inplace=True)
sns.barplot(x="Title", y="Survived", data=datas)
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9

代表女士的Mrs,Miss和代表社会高层的Master,Royalty的生存率远远高于代表男性的Mr和社会中低层的Officer。
(2)家庭特征的处理
在家庭大小特征的分析中我们可以知道,拥有不同家庭成员数量的人存活率不相同。在这里我们将存活率相似的部分归为一类,将家庭大小特征转化为分类型特征。
datas['Fam_size'] = datas['SibSp'] + datas['Parch'] + 1
datas.loc[datas['Fam_size']>7,'Fam_type']=0
datas.loc[(datas['Fam_size']>=2)&(datas['Fam_size']<=4),'Fam_type']=2
datas.loc[(datas['Fam_size']>4)&(datas['Fam_size']<=7)|(datas['Fam_size']==1),'Fam_type']=1
datas['Fam_type']=datas['Fam_type'].astype(np.int32)
sns.barplot(x="Fam_type", y="Survived", data=datas)
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8

代表拥有2—4位家庭成员的“Fam_type.2”拥有更高的存活率
(3)舱门数据处理
处理有大量缺失值的舱门数据。关键思想是:要将特征尽可能的处理为分类型特征。那么我们就有两种思路:①缺失值分一类,不缺失的值分为一类 ②缺失值分一类,剩下确定的值再细分类,很明显我们要选择第二种思路。现在我们将缺失值全部用‘U’来填补,已经确定的舱门号则提取出它的首字母作为它的新特征甲板号‘Board’
datas['Cabin'] = datas['Cabin'].fillna('U')
datas['Board']=datas['Cabin'].str.get(0)
sns.barplot(x="Board", y="Survived", data=datas)
- 1
- 2
- 3

(4)票号的处理
datas['Ticket'].value_counts()
- 1

可以看到,票号并不是单独唯一值,而是可以多个乘客同时拥有相同的票号的。
那么我们可以做出一个大胆的假设,这可能与我们的家属数据有关系,同票号的原因可能是因为同一个家庭共用一个票号,放在现实当中就是相当于购买了一张家庭票。
这样的话我们就可以根据某张票同票号的乘客数量来对特征进行分类。
Ticket_Counts = dict(datas['Ticket'].value_counts())
datas['TicketGroup'] = datas['Ticket'].apply(lambda x:Ticket_Counts[x])
sns.barplot(x='TicketGroup', y='Survived', data=datas)
- 1
- 2
- 3

可以看到,同票号数2~4的’ticket’存活率比其他都高,这与我们的家属数据‘FamilySize’有着相同的规律,所以我们的猜测应该是正确的。
datas.loc[datas['TicketGroup']>8,'Ticketlabels']=0
datas.loc[(datas['TicketGroup']>4)&(datas['TicketGroup']<=8)|(datas['TicketGroup']==1),'Ticketlabels']=1
datas.loc[(datas['TicketGroup']>=2)&(datas['TicketGroup']<=4),'Ticketlabels']=2
datas['Ticketlabels']=datas['Ticketlabels'].astype(np.int32)
sns.barplot(x='Ticketlabels', y='Survived', data=datas)
- 1
- 2
- 3
- 4
- 5

(5)港口号码的处理
datas[datas['Embarked'].isnull()]
- 1

港口号码的缺失值比较少,只有2个,一般我们可以直接用众数来进行填补。
但在泰坦尼克号数据集上,登舱的港口可能与社会等级还有票价挂钩,所以我们先看一下港口号和社会等级的关联。
datas.groupby(by=["Pclass","Embarked"]).Fare.median()
- 1

很明显在中低层级的人群中,C港口的登舱数量是最多的。在高层级的人群中,Q港口的登舱数量是最多的。所以我们选择将这两个缺失值填补为‘C’
datas['Embarked'] = datas['Embarked'].fillna('C')
- 1
(6)票价的处理(原理与港口号码的处理相同,根据社会等级和票价的关系进行填补)
datas[datas['Fare'].isnull()]
fare=datas[(datas['Embarked'] == "S") & (datas['Pclass'] == 3)].Fare.median()
datas['Fare']=datas['Fare'].fillna(fare)
- 1
- 2
- 3
(7)年龄的处理
由于年龄的缺失值非常的多,单独使用众数或者平均数进行填补是不合理的。而且与年龄相关的特征比较多,有社会等级,性别,姓名等等,所以我们采用另一个填补方法:随机森林回归树进行填补
from sklearn.ensemble import RandomForestRegressor
ages = datas[['Age', 'Pclass','Sex','Title']]
ages=pd.get_dummies(ages)
known_ages = ages[ages.Age.notnull()].values
unknown_ages = ages[ages.Age.isnull()].values
y = known_ages[:, 0]
X = known_ages[:, 1:]
rfr = RandomForestRegressor(random_state=60, n_estimators=100, n_jobs=-1)
rfr.fit(X, y)
pre_ages = rfr.predict(unknown_ages[:, 1::])
datas.loc[ (datas.Age.isnull()), 'Age' ] = pre_ages
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
(8)异常值处理(此处借鉴了kaggle上大神的经验,对模型的提高比较明显,上升了1%的正确率。)
把姓氏相同的乘客划分为同一组,从人数大于一的组中分别提取出每组的妇女儿童和成年男性。
datas['Surname']=datas['Name'].apply(lambda x:x.split(',')[0].strip())
Surname_Count = dict(datas['Surname'].value_counts())
datas['FamilyGroup'] = datas['Surname'].apply(lambda x:Surname_Count[x])
Female_Child_Group=datas.loc[(datas['FamilyGroup']>=2) & ((datas['Age']<=12) | (datas['Sex']=='female'))]
Male_Adult_Group=datas.loc[(datas['FamilyGroup']>=2) & (datas['Age']>12) & (datas['Sex']=='male')]
- 1
- 2
- 3
- 4
- 5
发现绝大部分女性和儿童组的平均存活率都为1或0,即同组的女性和儿童要么全部幸存,要么全部遇难。
Female_Child=pd.DataFrame(Female_Child_Group.groupby('Surname')['Survived'].mean().value_counts())
Female_Child.columns=['GroupCount']
sns.barplot(x=Female_Child.index, y=Female_Child["GroupCount"]).set_xlabel('AverageSurvived')
- 1
- 2
- 3

绝大部分成年男性组的平均存活率也为1或0。
Male_Adult=pd.DataFrame(Male_Adult_Group.groupby('Surname')['Survived'].mean().value_counts())
Male_Adult.columns=['GroupCount']
Male_Adult
- 1
- 2
- 3
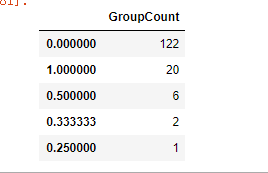
普遍规律是女性和儿童幸存率高,成年男性幸存较低,所以我们把不符合普遍规律的反常组选出来单独处理。把女性和儿童幸存率为0的组设置为遇难组,把成年男性存活率为1的组设置为幸存组。
Female_Child_Group=Female_Child_Group.groupby('Surname')['Survived'].mean()
Dead_List=set(Female_Child_Group[Female_Child_Group.apply(lambda x:x==0)].index)
print(Dead_List)
Male_Adult_List=Male_Adult_Group.groupby('Surname')['Survived'].mean()
Survived_List=set(Male_Adult_List[Male_Adult_List.apply(lambda x:x==1)].index)
print(Survived_List)
- 1
- 2
- 3
- 4
- 5
- 6
为了使处于这两种反常组中的样本能够被正确分类,对测试集中处于反常组中的样本的Age,Title,Sex进行惩罚修改。
train=datas.loc[datas['Survived'].notnull()]
test=datas.loc[datas['Survived'].isnull()]
test.loc[(test['Surname'].apply(lambda x:x in Dead_List)),'Sex'] = 'male'
test.loc[(test['Surname'].apply(lambda x:x in Dead_List)),'Age'] = 60
test.loc[(test['Surname'].apply(lambda x:x in Dead_List)),'Title'] = 'Mr'
test.loc[(test['Surname'].apply(lambda x:x in Survived_List)),'Sex'] = 'female'
test.loc[(test['Surname'].apply(lambda x:x in Survived_List)),'Age'] = 5
test.loc[(test['Surname'].apply(lambda x:x in Survived_List)),'Title'] = 'Miss'
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
(9)重新划分数据,分出训练集和测试集
datas=pd.concat([train, test])
datas=datas[['Survived','Pclass','Sex','Age','Fare','Embarked','Title','Fam_type','Board','Ticketlabels']]
datas=pd.get_dummies(datas)
train=datas[datas['Survived'].notnull()]
test=datas[datas['Survived'].isnull()].drop('Survived',axis=1)
X = train.values[:,1:]
y = train.values[:,0]
- 1
- 2
- 3
- 4
- 5
- 6
- 7
Part3.数据建模和调参优化
(1)模型的选择
模型的选择非常关键,kaggle社区中大部分参赛选手使用的是随机森林分类器,这说明决策树在我们泰坦尼克号数据集上有着比较好的效果。而博主第一次进行建模的时候使用的是svc,经过svc的kernel参数的调参得出,这是一个线性的数据集,虽然用svc处理能够得到比较好的效果,但处理线性数据我们有更好的选择:逻辑回归
(2)利用逻辑回归建模与调参优化
建立逻辑回归模型并画出第一个重要参数C的学习曲线,找到最佳的C值
from sklearn.linear_model import LogisticRegression as LR from sklearn.metrics import accuracy_score import matplotlib.pyplot as plt from sklearn.feature_selection import SelectFromModel from sklearn.model_selection import cross_val_score from sklearn.ensemble import RandomForestClassifier fullx = [] fsx = [] C=np.arange(0.01,10.01,0.5) for i in C: LR_ = LR(solver="liblinear",C=i,random_state=420) fullx.append(cross_val_score(LR_,X,y,cv=10).mean()) X_embedded = SelectFromModel(LR_,norm_order=1).fit_transform(X,y) fsx.append(cross_val_score(LR_,X_embedded,y,cv=10).mean()) print(max(fsx),C[fsx.index(max(fsx))]) plt.figure(figsize=(20,5)) plt.plot(C,fullx,label="full") plt.plot(C,fsx,label="feature selection") plt.xticks(C) plt.legend() plt.show()
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
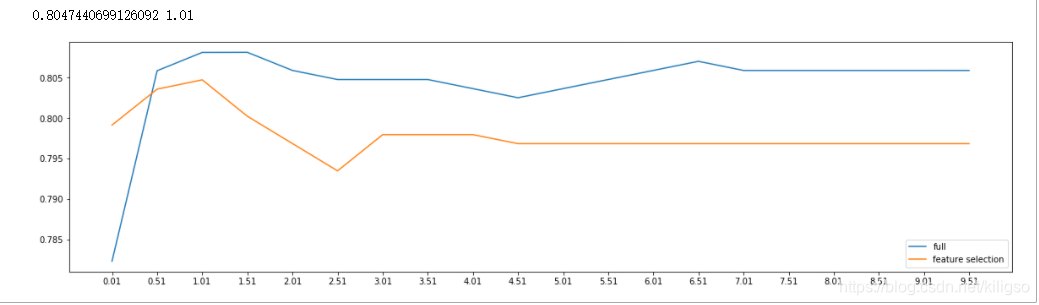
通过曲线可以找到最佳的C值在1.01附近,我们再一次对C值的范围进行细分,找到最终的C值
fullx = [] fsx = [] C=np.arange(0.55,1.55,0.005) for i in C: LR_ = LR(solver="liblinear",C=i,random_state=420) fullx.append(cross_val_score(LR_,X,y,cv=10).mean()) X_embedded = SelectFromModel(LR_,norm_order=1).fit_transform(X,y) fsx.append(cross_val_score(LR_,X_embedded,y,cv=10).mean()) print(max(fsx),C[fsx.index(max(fsx))]) plt.figure(figsize=(20,5)) plt.plot(C,fullx,label="full") plt.plot(C,fsx,label="feature selection") plt.xticks(C) plt.legend() plt.show()
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
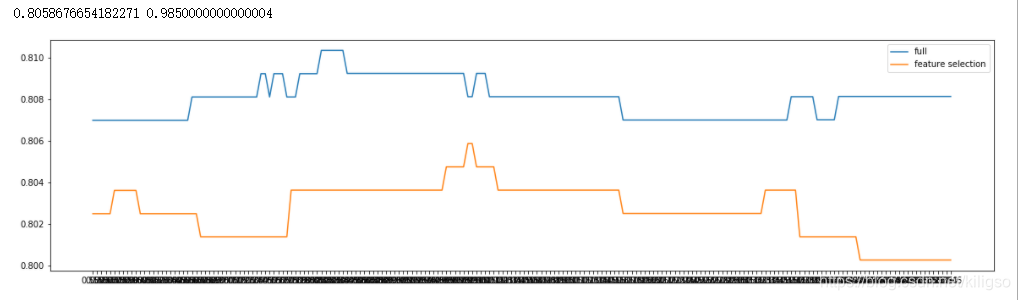
找到了最佳的C值:0.9850000000000004,将它代到我们的模型中,并开始调整第二个关键参数max_iter,同样的,我们画出max_iter的学习曲线
from sklearn.model_selection import train_test_split l2 = [] l2test = [] Xtrain, Xtest, Ytrain, Ytest = train_test_split(X,y,test_size=0.3,random_state=420) for i in np.arange(1,201,10): lrl2 = LR(penalty="l2",solver="liblinear",C=0.9850000000000004,max_iter=i) lrl2 = lrl2.fit(Xtrain,Ytrain) l2.append(accuracy_score(lrl2.predict(Xtrain),Ytrain)) l2test.append(accuracy_score(lrl2.predict(Xtest),Ytest)) graph = [l2,l2test] color = ["black","gray"] label = ["L2","L2test"] plt.figure(figsize=(20,5)) for i in range(len(graph)): plt.plot(np.arange(1,201,10),graph[i],color[i],label=label[i]) plt.legend(loc=4) plt.xticks(np.arange(1,201,10)) plt.show()
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
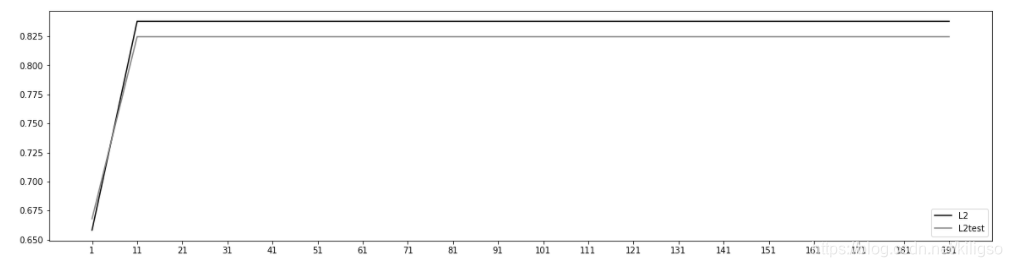
可以看到max_iter在11之后对模型的作用已经达到了上限,所以可以取一个任意值,博主使用的是200。现在用我们得到的最佳参数来进行建模C=0.9850000000000004,max_iter=200
lr = LR(penalty="l2",solver="liblinear",C=0.9850000000000004,max_iter=200).fit(X,y)
cross_val_score(lr,X,y,cv=10).mean()
- 1
- 2
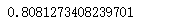
交叉验证的得分还不错,达到了80.8%
predictions = lr.predict(test)
test=pd.read_csv('test.csv')
PassengerId=test['PassengerId']
prdict_test = pd.DataFrame({"PassengerId": PassengerId, "Survived": predictions.astype(np.int32)})
prdict_test.to_csv("prdict_test.csv", index=False)
- 1
- 2
- 3
- 4
- 5
最后保存并上传到kaggle上,就可以对模型进行评分
Part4.总结
泰坦尼克号数据集的做法还有很多很多,例如将Age年龄进行分类的,fare票价进行分类的,办法很多很多。我只是抛砖引玉,分享了自己经验,如果有更好的方法,可以在评论区告诉我
希望能对你们有帮助!



