Sift特征_sift特征 长度

说明：本篇博客只围绕sift描述子展开了学习。对于sift关键点检测涉及的内容并未进行详细的分析和学习。相关内容可参考本篇博客中的参考文献。

Sift特征

Sift特征包含两个部分，一个是关键点（frame或者keypoint），另外一个就是在关键点处的描述子(descriptor,或者Keypoint descriptor)，更确切的说是关键点所在尺度空间的描述子。

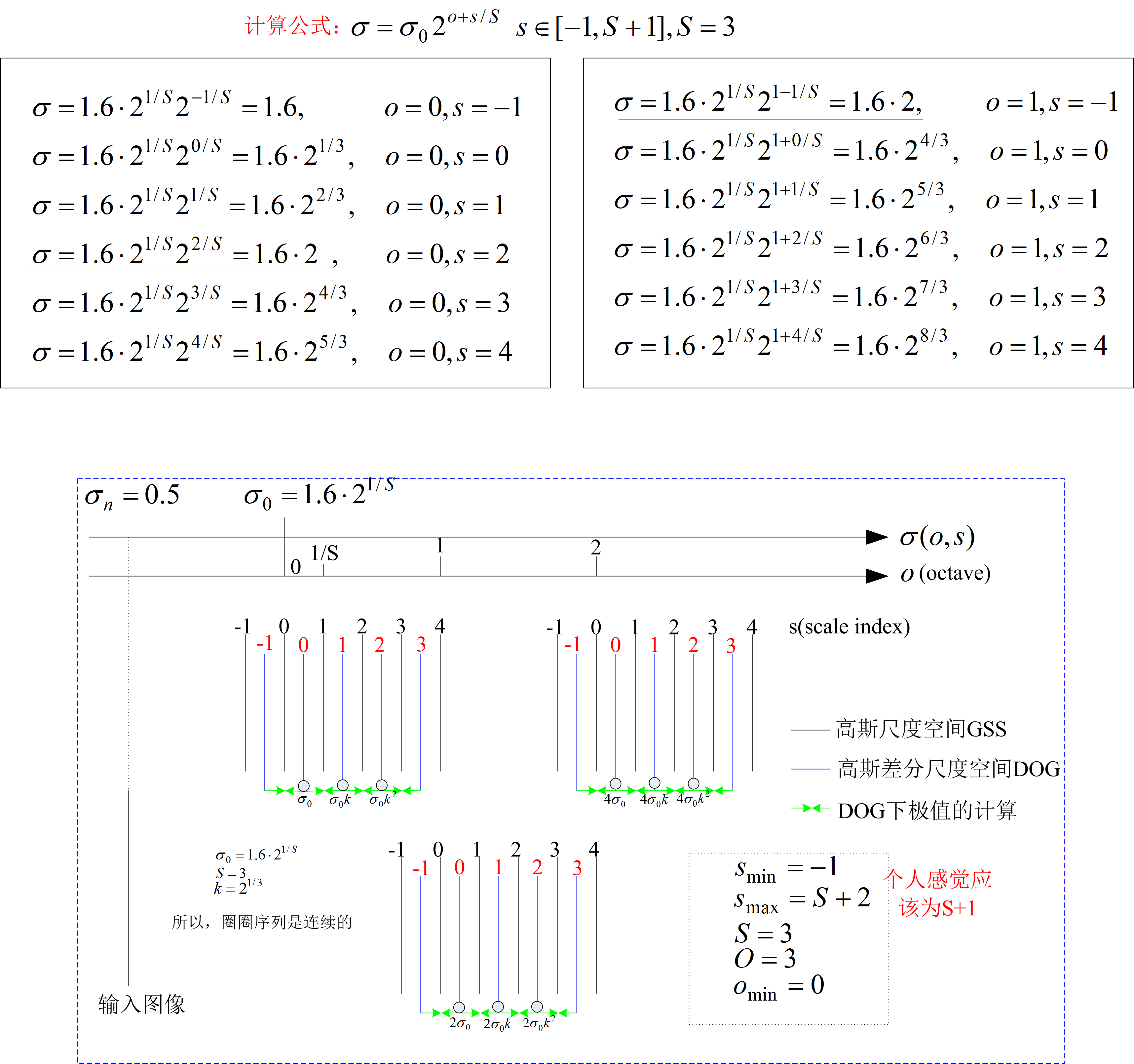
很多文章中给出了两种尺度空间：高斯尺度空间GSS和高斯差分尺度空间DOG。可能会怀疑，到底描述子是在哪个尺度空间计算的？其实采用的是高斯尺度空间。如下图：GSS对图像使用[-1,4]不同尺度的高斯进行平滑得到图像，其索引号[-1,4]指明了不同的尺度，DOG索引号为[-1,3]只是表示与GSS索引号对应的关系，并且图中还给出了”DOG下极值的计算“的索引号，其为GSS的中间三个，即[0,2]。例如，如果我们在”DOG下极值的计算“，发现在其索引号为0尺度有满足条件的关键点，那么该关键点所处的尺度空间就是：$s=0$的高斯尺度空间。

在面部特征点的检测中，经常提取Sift特征。这里的Sift特征指的就是Sift描述子，在一个点处提取的Sift特征一般为128维，即4*4*8=128,4*4表示4*4的区域，8表示每个区域统计的方向。

在Vfleat中:frame 表示Keypoint,descriptor 表示Keypoint descriptor

自定义关键点：

vl_sift函数可以自定义关键点，然后计算该关键点处的描述子。
1

例如我们可以计算关键点在(100,100)，尺度为10,方向为$-\frac{\pi}{8}$的描述子：

fc=[100;100;10;-pi/8];
[f,d]=vl_sift(I,'frames',fc);
1
2

我们不指定方向，使用关键点的方向，即将方向参数设置为0，并通过参数’orientations’指定，则：

fc=[100;100;10;0];
[f,d]=vl_sift(I,'frames',fc,'orientations');
1
2

也可以将参数fc设置为矩阵的形式，一次计算多个关键点的描述子。特别的，一个关键点可能有多个方向，或者没有方向（图像区域为常数）

问题就来了，这里的尺度是什么？描述子的方向怎么计算的呢？如果方向是指描述子的主方向，那么通过直方图确定主方向时采用的邻域是多大呢？
如上面的函数，我们传入的尺度为10，是使用标准差为$\sigma=10$的高斯对图像进行平滑后，然后进行后面的处理吗？等等一连串的问题，使得我很模糊。
下图给出了高斯尺度示意图，其中左右表格内画红色的下划线的表示（这里我们下表都从0开始）：第1层的第0个图像，是从第0层的第3个图像下采样得到，随后第1层的第1个图像是由第1层的第0个图像再经过高斯标准差为$\sqrt{\sigma_{(1,0)}^2-\sigma_{(1,-1)}^2}$的高斯平滑后得到的，以次类推。。。

Vlfeat库的配置：

Vlfeat的源程序使用C语言编写，读起来和使用起来也着实让人费力。由于Vlfeat给出了能够计算给定关键点的描述子的Matlab接口函数。那么我们Matlab入口运行程序进行学习分析。
Vlfeat提供的两个版本：
(1).vlfeat-0.9.20-bin.tar.gz （编译好的二进制文件）
(2).vlfeat-0.9.20 （源文件）

1.下载完vlfeat-0.9.20后，将其解压到当前文件夹，在目录下，有个Makefile.mak文件。使用写字板或者Notepad打开，该文件内给出了需要修改的详细说明，即Customization（定制）部分。

#                                                        Customization
# --------------------------------------------------------------------
# To modify this script to run on your platform it is usually
# sufficient to modify the following variables:
#
# ARCH: Either win32 or win64 [win64]
# DEBUG: Set to yes to ativate debugging [no]
# MATLABROOT: Path to MATLAB
# MSVSVER: Visual Studio version (e.g. 80, 90, 100) [90 for VS 9.0]
# MSVCROOT: Visual C++ location [$(VCInstallDir)].
# WINSDKROOT: Windows SDK location [$(WindowsSdkDir)]
#
# Note that some of these variables depend on the architecture
# (either win32 or win64).
1
2
3
4
5
6
7
8
9
10
11
12
13
14

修改截图如下：

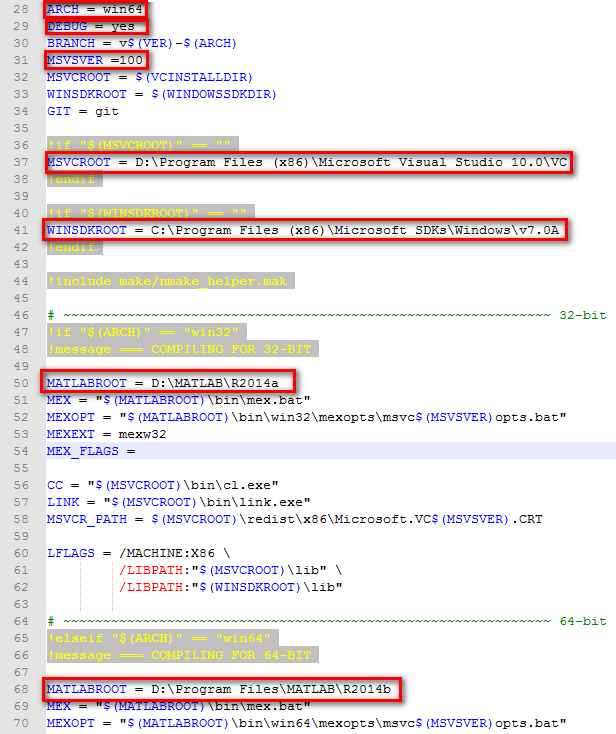
我们电脑上装了两个Matlab，R2014a是32位的，R2014b是64位的。

2.
方法1：双击vlfeat.vcproj打开，进入VS2010界面，点击直到完成后，在左侧的解决方案一栏，对vlfeat进行编译，即build即可。
方法2：在电脑程序目录下，找到Visio Studio Tools找到类似于Visual Studio x64 Win64 命令提示(2010)的工具，点击运行，然后在dos下，将目录切换到vlfeat-0.9.20目录，然后利用nmake命令：

nmake /f Makefile.mak
1

3.目的：将mex.c文件编译成供Matlab调用的二进制文件。
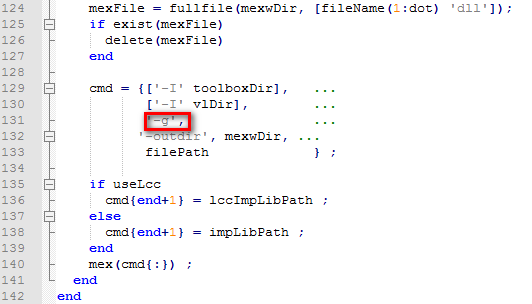
打开Matlab，将工程目录切换到vlfeat-0.9.20\toolbox目录下，首先修改一下vl_compile.m文件，即将mex -o，修改为mex -g，如下：

调试Sift源文件

1.打开Matlab，当然首先是要设置好包含路径，主页-设置路径-添加并包含子文件夹，将vlfeat-0.9.20添加进去。我为了省事，一般都是直接将所有的添加进去，你可以选择只需要将toolbox/mex添加到Matlab路径中。然后书写简单的代码：

%clc;clearvars;
% prepare data
imgPath='E:\data\lfw\imgs\Aaron_Eckhart\Aaron_Eckhart_0001.jpg';
bbox=[63 72 126+63 126+72];
landmark=[34 35; 53 38; 41 86; 75 90; 58 93; 59 87 ;72 40 ;94 43; 48 70; 72 72];
nlandmark=10;
isShow=false;
for i=1:nlandmark
    landmark(i,1)=landmark(i,1)+bbox(1);
    landmark(i,2)=landmark(i,2)+bbox(2);
end

if isShow
    figure(1);
    subplot(2,1,1);
    img=imread(imgPath);
    img_gray=rgb2gray(img);
    imshow(img_gray);
    hold on;
    for i=1:nlandmark
        plot(landmark(i,1),landmark(i,2),'.r','markersize',8);
    end
    % for box;
    rmpath('E:\matlabworkplace\headpose_with_block\third_part\vlfeat-0.9.20\toolbox\noprefix');
    plotbox(bbox,'r');
    addpath('E:\matlabworkplace\headpose_with_block\third_part\vlfeat-0.9.20\toolbox\noprefix');
end

% I = vl_impattern('roofs1') ;
% image(I) ;
% I = single(rgb2gray(I)) ;
% [f,d] = vl_sift(I) ;
% perm = randperm(size(f,2)) ;
% sel = perm(1:50) ;
% h1 = vl_plotframe(f(:,sel)) ;
% h2 = vl_plotframe(f(:,sel)) ;
% set(h1,'color','k','linewidth',3) ;
% set(h2,'color','y','linewidth',2) ;

pi=3.1415926;
img=imread(imgPath);
figure(1);
%subplot(1,2,1);
image(img);
img_gray=rgb2gray(img);
I=single(img_gray);
hold on;
ori=[pi/8 2*pi/8 3*pi/8 4*pi/8 5*pi/8 6*pi/8 7*pi/8 pi -pi/8 -2*pi/8];
%scale=[1 2 3 4 5 6 7 8 9 10];
scale=[1.6 1.6 1.6 1.6 1.6 1.6 1.6 1.6 1.6 1.6];
for i=1:10
    plot(landmark(i,1),landmark(i,2),'.r','markersize',16);
    fc=[landmark(i,1);landmark(i,2);scale(i);ori(i)];
    [f,d]=vl_sift(I,'frames',fc);
    h1=vl_plotframe(f(:,1));
    h2=vl_plotframe(f(:,1));
    set(h1,'color','k','linewidth',3);
    set(h2,'color','y','linewidth',2);
    name=num2str(i);
    text(landmark(i,1),landmark(i,2),name);
end
%%上面的代码可以不需要，只需要下面的代码。
figure(2);
img2 = vl_impattern('roofs1') ;
image(img2) ;
img2 = single(rgb2gray(img2)) ;
[f,d] = vl_sift(img2) ;
perm = randperm(size(f,2)) ;
sel = perm(1:50) ;
h1 = vl_plotframe(f(:,sel)) ;
h2 = vl_plotframe(f(:,sel)) ;
set(h1,'color','k','linewidth',3) ;
set(h2,'color','y','linewidth',2) ;
h3 = vl_plotsiftdescriptor(d(:,sel),f(:,sel)) ;
set(h3,'color','g') ;
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76

2.打开VS2010，通过菜单中的文件-打开-文件，将vlfeat-0.9.20\toolbox\sift下的vl_sift.c和vlfeat-0.9.20\vl下的sift.c添加到VS中，然后在两个文件中，设置断点就可以了。
3.在VS2010中设置为断点后，在VS菜单中工具-附加到进程，在可用进程中找到Matlab，然后双击即可。
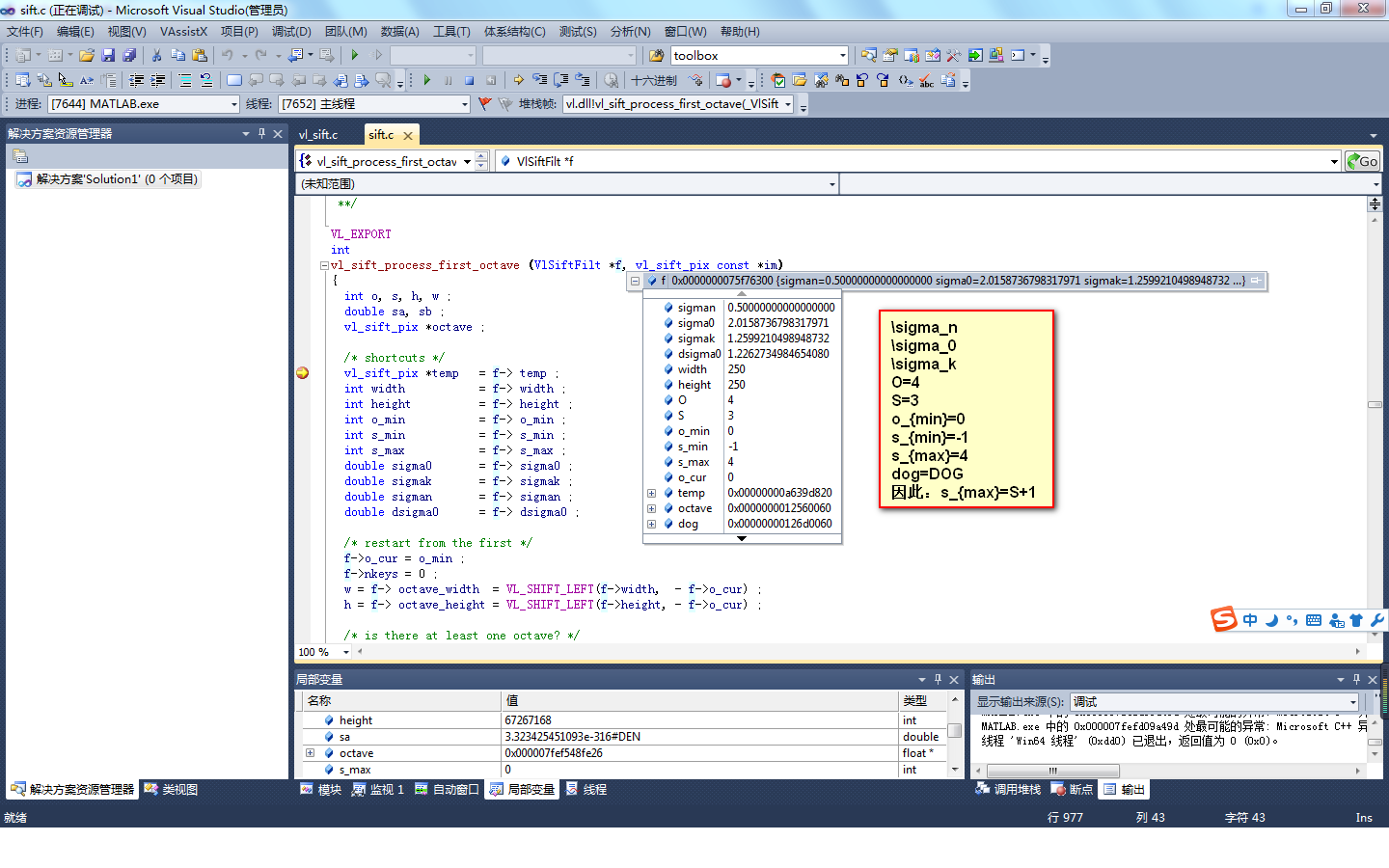
4.运行Matlab程序，会自动跳转到VS2010设置的断点处，通过F5进行断点的切换。如下图：

参数说明

公式1：

$$G(x;\sigma)=(g_{\sigma}*I)(x)$$
其中 $g_{\sigma}$是各向同性高斯核，方差为 ${\sigma}^2I$。
公式2:
$$\sigma(o,s)=\sigma_0 2^{o+s/S},o\in o_\mathrm{min}+[0,...,O-1],s\in[0,...,S-1]$$
注意这里的 $s\in[0,...,S-1]$也着实让人迷惑的，你会在后面看到文章中又有 $s \in[s_\mathrm{min},s_\mathrm{max}]$,其中 $s_\mathrm{min}=-1$, $s_\mathrm{max}=S+1$

检测器参数：

SIFT frame（即关键点）是差分尺度空间的局部极值点。这样的点的选择通过下面的参数控制：

描述子参数：
SIFT描述子是一个带有权重和插值的直方图，其利用梯度方向和关键点周围的块区域的位置进行计算。描述子有下面的参数：

代码的分析

高斯模板

一维高斯:

$$G(x,\sigma)=\frac{1}{\sqrt{2\pi {\sigma}^2}} e^{\frac{-x^2}{2 {\sigma}^2}}$$
二维高斯：
$$G(x,y,\sigma I)=G(x,\sigma)\cdot G(y,\sigma)=\frac{1}{\sqrt{2\pi {\sigma}^2}} e^{\frac{-x^2}{2 {\sigma}^2}}\cdot \frac{1}{\sqrt{2\pi {\sigma}^2}} e^{\frac{-y^2}{2 {\sigma}^2}}=\frac{1}{{2\pi {\sigma}^2}} e^{\frac{-({x^2+y^2})}{2 {\sigma}^2}}$$

其中$I$是2*2的单位阵。$x,y$具有同样的标准差$\sigma$。
从上面的公式，直观上我们感觉二维高斯卷积操作可以分解为分别经过$x,y$方向的一维操作。这里的“卷积”相当于“相关”。其中$x,y$表示与模板中心的位移。

证明：

$$G(x,y)*I(x,y)=G(x)*(G(y)*I(x,y))$$

$$\begin{equation} \begin{aligned} G(x,y)*I(x,y) &=\int_{\tau} \int_{t}G(\tau,t)I(\tau-x,t-y)dtd\tau\\ &=\int_{\tau} \int_{t}G(\tau)G(t)I(\tau-x,t-y)dt d\tau\\ &=\int_{\tau} G(\tau)\left (\int_{t}G(t)I(\tau-x,t-y)dt \right) d\tau \end{aligned} \end{equation}$$
其中
$$\int_{t}G(t)I(\tau-x,t-y)dt =G(y)*I(\tau-x,y)$$
而：
$$\int_{\tau} G(\tau)\left (\int_{t}G(t)I(\tau-x,t-y)dt \right) d\tau =G(x)*(G(y)*I(\tau-(\tau-x),y))=G(x)*G(y)*I(x,y)$$
平滑的高斯模板是多大的呢？即多少个像素呢？其是否与现在使用的高斯标准差（即尺度 $\sigma$）有关呢？
代码中给出了计算：
高斯模板的宽度=$\mathrm{max}(\left \lceil 4*\sigma \right \rceil,1)$，这里的宽度是半径，例如对于5*5，则宽度为2，对于7*7，则宽度为3，因此高斯模板的大小为：

$$2*\mathrm{max}(\left \lceil 4*\sigma \right \rceil,1)+1$$

static void
_vl_sift_smooth (VlSiftFilt * self,
                 vl_sift_pix * outputImage,
                 vl_sift_pix * tempImage,
                 vl_sift_pix const * inputImage,
                 vl_size width,
                 vl_size height,
                 double sigma)
{
  /* prepare Gaussian filter */
  if (self->gaussFilterSigma != sigma) {
    vl_uindex j ;
    vl_sift_pix acc = 0 ;//vl_sift_pix即float
    if (self->gaussFilter) vl_free (self->gaussFilter) ;
    self->gaussFilterWidth = VL_MAX(ceil(4.0 * sigma), 1) ;
    self->gaussFilterSigma = sigma ;//$\sigma$
    self->gaussFilter = vl_malloc (sizeof(vl_sift_pix) * (2 * self->gaussFilterWidth + 1)) ;//高斯滤波器,二维滤波可以等价分别x方向一维滤波，然后y方向的一维滤波，或者反过来。

    for (j = 0 ; j < 2 * self->gaussFilterWidth + 1 ; ++j) {
      vl_sift_pix d = ((vl_sift_pix)((signed)j - (signed)self->gaussFilterWidth)) / ((vl_sift_pix)sigma) ;//到高斯模板中心的偏移
      self->gaussFilter[j] = (vl_sift_pix) exp (- 0.5 * (d*d)) ;//这里并不需要乘以\frac{1}{\sqrt{2\pi\sigma}}，因为每一项都有同样的。
      acc += self->gaussFilter[j] ;
    }
    for (j = 0 ; j < 2 * self->gaussFilterWidth + 1 ; ++j) {
      self->gaussFilter[j] /= acc ;//将高斯权重归一化，使其和为1
    }
  }

  if (self->gaussFilterWidth == 0) {
    memcpy (outputImage, inputImage, sizeof(vl_sift_pix) * width * height) ;
    return ;
  }
  //进行一维卷积操作
  vl_imconvcol_vf (tempImage, height,
                   inputImage, width, height, width,
                   self->gaussFilter,
                   - self->gaussFilterWidth, self->gaussFilterWidth,
                   1, VL_PAD_BY_CONTINUITY | VL_TRANSPOSE) ;

  vl_imconvcol_vf (outputImage, width,
                   tempImage, height, width, height,
                   self->gaussFilter,
                   - self->gaussFilterWidth, self->gaussFilterWidth,
                   1, VL_PAD_BY_CONTINUITY | VL_TRANSPOSE) ;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46

例如

尺度$\sigma=1.6$,则进行标准差为$\sqrt{\sigma^2-\sigma_n^2}=1.5199$的高斯平滑，即利用$G_{1.5199}(x,y)$对图像$I$进行平滑，其中高斯模板的大小，通过上面的红色求得为7*7。计算描述子实际窗口的区域的大小为：

$$\frac{3\sigma *\mathrm{NumSpatialBins}*\sqrt 2}{2}$$
考虑到像素的加权和插值，因此在上面公式加上1（下面有详解，并可参考下面的空间差值图）。乘以$\sqrt{2}$是考虑到块区域的旋转。变成：

$$\frac{3\sigma *(\mathrm{NumSpatialBins}+1)*\sqrt 2}{2}$$

附录：
两个高斯函数的卷积仍然为一个高斯函数，满足方差为两个高斯函数之和，即：

$$\sigma_1^2+\sigma_2^2=\sigma_3^2$$
因为二维高斯可以分解为分别进行x方向的一维高斯和y方向的一维高斯。所以这里只推导一维的情况。为了描述的统一和简洁，我们用小写的 $g_1(x)$来表示一维高斯。
参考： http://blog.csdn.net/liguan843607713/article/details/42215965
一维高斯：
$$g_1(x)=\frac{1}{\sqrt{2\pi}\sigma_1}e^{-\frac{x^2}{2\sigma_1^2}},g_2(x)=\frac{1}{\sqrt{2\pi}\sigma_2}e^{-\frac{x^2}{2\sigma_2^2}}$$
我们令 $f(x)$表示两个高斯函数的卷积,即：
$$\begin{equation} \begin{aligned} f(x)=g_1(x)*g_2(x)&=\int_{-\infty}^{\infty}g_1(t)g_2(x-t)dt \\ &=\int_{-\infty}^{\infty}g_1(x-t)g_2(t)dt \end{aligned} \end{equation}$$
我们写出完整的式子：
$$\begin{equation} \begin{aligned} f(x)&=\int_{-\infty}^{\infty}\frac{1}{\sqrt{2\pi}\sigma_1}e^{-\frac{t^2}{2\sigma_1^2}}\frac{1}{\sqrt{2\pi}\sigma_2}e^{-\frac{(x-t)^2}{2\sigma_2^2}}dt \\ &=\frac{1}{{2\pi}\sigma_1\sigma_2}\int_{-\infty}^{\infty}e^{-\left [\frac{t^2}{2\sigma_1^2}+\frac{(x-t)^2}{2\sigma_2^2}\right]}dt\\ &=\frac{1}{{2\pi}\sigma_1\sigma_2}\int_{-\infty}^{\infty}e^{-\left [ \left( \frac{1}{2\sigma_1^2}+\frac{1}{2\sigma_2^2}\right)t^2-\left (\frac{2x}{2\sigma_2^2}\right)t+\frac{x^2}{2\sigma_2^2}\right]}dt\\ &=\frac{1}{{2\pi}\sigma_1\sigma_2}e^{-\frac{x^2}{2\sigma_2^2}}\int_{-\infty}^{\infty}e^{-\left [ \left( \frac{1}{2\sigma_1^2}+\frac{1}{2\sigma_2^2}\right)t^2-\left (\frac{x}{\sigma_2^2}\right)t\right]}dt\\ 令a= \frac{1}{2\sigma_1^2}+\frac{1}{2\sigma_2^2},b=\frac{x}{\sigma_2^2},则上式变成为：\\ &=\frac{1}{{2\pi}\sigma_1\sigma_2}e^{-\frac{x^2}{2\sigma_2^2}}\int_{-\infty}^{\infty}e^{-\left ( at^2-bt\right)}dt \qquad (公式1)\\ \end{aligned} \end{equation}$$

我们发现$e^{-at^2}$可以通过下面的形式计算:

$$\begin{equation} \begin{aligned} \int_{-\infty}^{\infty}e^{-x^2}dx=\sqrt{\pi},其转化为极坐标形式进行推导（略）。 \end{aligned} \end{equation}$$
而和 $e^{bt}$的定积分都没法求解。因此，我们利用变量代换的形式，将 $e^{bt}$的形式进行消掉，公式（1）转变为：
$$\begin{equation} \begin{aligned} f(x)&=\frac{1}{{2\pi}\sigma_1\sigma_2}e^{-\frac{x^2}{2\sigma_2^2}}\int_{-\infty}^{\infty}e^{-a\left (t^2-\frac{b}{a}t+\frac{b^2}{4a^2}-\frac{b^2}{4a^2}\right)}dt\\ &=\frac{1}{{2\pi}\sigma_1\sigma_2}e^{-\frac{x^2}{2\sigma_2^2}+\frac{b^2}{4a}}\int_{-\infty}^{\infty}e^{-a\left (t-\frac{b}{2a}\right)^2}dt \\ 令t-\frac{b}{2a}=\tau,则上式变成为:\\ &=\frac{1}{{2\pi}\sigma_1\sigma_2}e^{-\frac{x^2}{2\sigma_2^2}+\frac{b^2}{4a}}\int_{-\infty}^{\infty}e^{-a \tau^2}d\tau\\ &=\frac{1}{{2\pi}\sigma_1\sigma_2}e^{-\frac{x^2}{2\sigma_2^2}+\frac{b^2}{4a}} \frac{1}{\sqrt{a}}\int_{-\infty}^{\infty}e^{-(\sqrt{a} \tau)^2}d(\sqrt{a}\tau)\\ &=\frac{1}{{2\pi}\sigma_1\sigma_2}e^{-\frac{x^2}{2\sigma_2^2}+\frac{b^2}{4a}} \frac{1}{\sqrt{a}}\sqrt{\pi}\\ 将b和a的表达式带入到上式：\\ &=\frac{1}{{2\pi}\sigma_1\sigma_2}e^{-\frac{x^2}{2\sigma_2^2}+\frac{\frac{x^2}{\sigma_2^4}}{4(\frac{1}{2\sigma_1^2}+\frac{1}{2\sigma_2^2})}} \frac{1}{\sqrt{(\frac{1}{2\sigma_1^2}+\frac{1}{2\sigma_2^2})}}\sqrt{\pi}\\ &=\frac{1}{{2\pi}\sigma_1\sigma_2}\frac{1}{\sqrt{(\frac{1}{2\sigma_1^2}+\frac{1}{2\sigma_2^2})}}\sqrt{\pi}\cdot e^{-\frac{x^2}{2\sigma_2^2}+\frac{\frac{x^2}{\sigma_2^4}}{4(\frac{1}{2\sigma_1^2}+\frac{1}{2\sigma_2^2})}} \\ &=\frac{1}{\sqrt{2\pi(\sigma_1^2+\sigma_2^2)}}\cdot e^{-\frac{x^2}{2(\sigma_1^2+\sigma_2^2)}} \end{aligned} \end{equation}$$

上面是一维连续高斯的卷积的证明。因此在取高斯窗口大小时采用了:

$$2*\mathrm{max}(\left \lceil 4*\sigma \right \rceil,1)+1$$
就是为了近似的满足上面卷积的要求。即高斯积分的取值范围为( $-\infty,+\infty$),即涵盖了高斯的所有取值。而满足上面的大小的窗口能够涵盖高斯的主要取值，所以在离散的空间，经过 $\sigma_2$高斯平滑， 近似的等价于先经过 $\sigma_1$的高斯平滑，在经过 $\sqrt{\sigma_2^2-\sigma_1^2}$的高斯平滑（注意这里的 $\sigma_2>\sigma_1$）。

sift描述子的计算

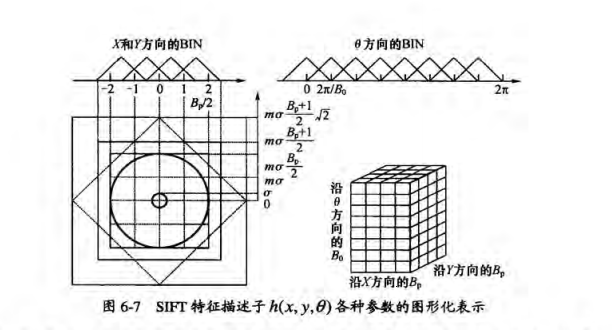
上面的图片来至于：《图像局部不变性特征与描述》，其很好的描述了当前图像所在的尺度和实际像素大小的关系。$B_p$就是上面描述的NumSpatialBins，$m=3$:

$$\begin{equation} \begin{aligned} \sigma \text{表示当前描述子所在的尺度}\\ m\sigma \text{表示一个空间bin的实际像素大小}\\ m \sigma \frac{B_p}{2} \text{表示4*4空间的半径} \\ m \sigma \frac{B_p+1}{2} \text{考虑到像素的加权和插值，在x(或y)的正负方向扩展了半个bin}\\ m \sigma \frac{B_p+1}{2}{\sqrt{2}} \text{考虑到图像的旋转} \end{aligned} \end{equation}$$
下面是VLFeat中描述子计算的代码：

Since weighting and interpolation of pixel is used, the support extends by another half bin.
因为使用了像素的加权和插值，支撑范围扩展了半个bin的像素大小。

下图描述了两种度量单位：1 bin为单位，以及像素单位。1bin=$m \sigma$,其中在计算插值时，采用的像素空间为连续的取值。

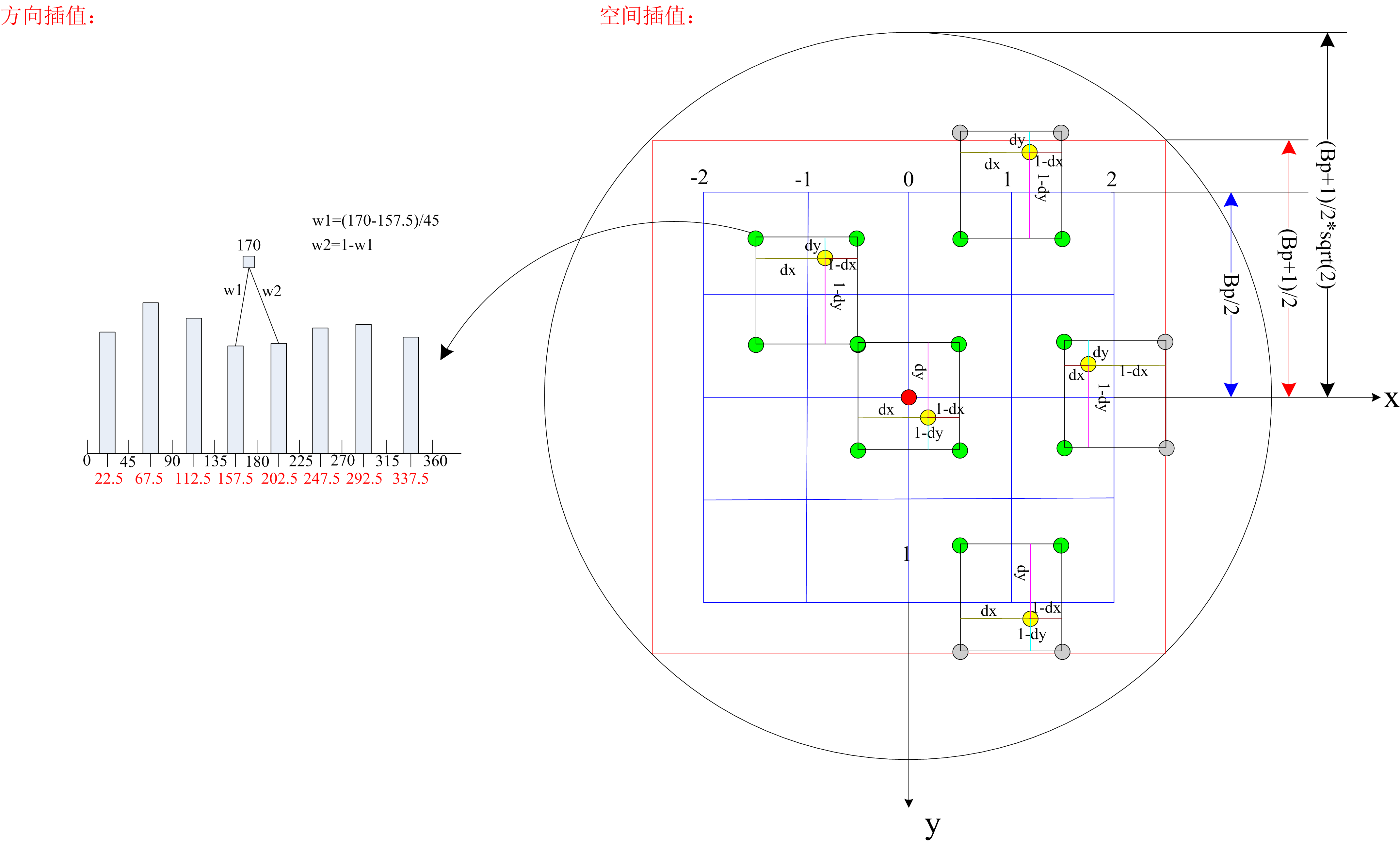
空间插值：
下图右侧给出了空间方向的插值，其中大小为4*4的空间bin,图中长度的度量方式均是采用1个bin为单位。黄色的点表示当前的像素点，都带有：空间位置，梯度和梯度方向属性，其有4个邻域，其中绿色的点表示每个bin的中心，灰色的点不在bin的范围内。
方向插值：
下图，左侧给出了一个空间bin中的方向的直方图统计（采用梯度幅值进行了加权，看箭头），其中170表示当前某个像素处的梯度方向，其介于157.5和202.5（分别对应于每个bin的中心）之间，那么该像素的梯度在这两个方向bin上的加权分别为w1和w2,w1=(170-157.5)/45,w2=1-w1，其中45为bin的宽度。即将360分成8个bin，每个bin的宽度为45.

对于一个像素（即当前关键点所在的尺度图像中的一个像素），其空间位置确定了其有4个邻域，其方向确定了其有2个方向的邻域。因此共4*2=8个邻域。即利用该像素的梯度对4个相邻空间bin的每两个方向bin进行加权。

有兴趣的话，可以将空间插值和方差插值画在一起，即画在一个三维图中。

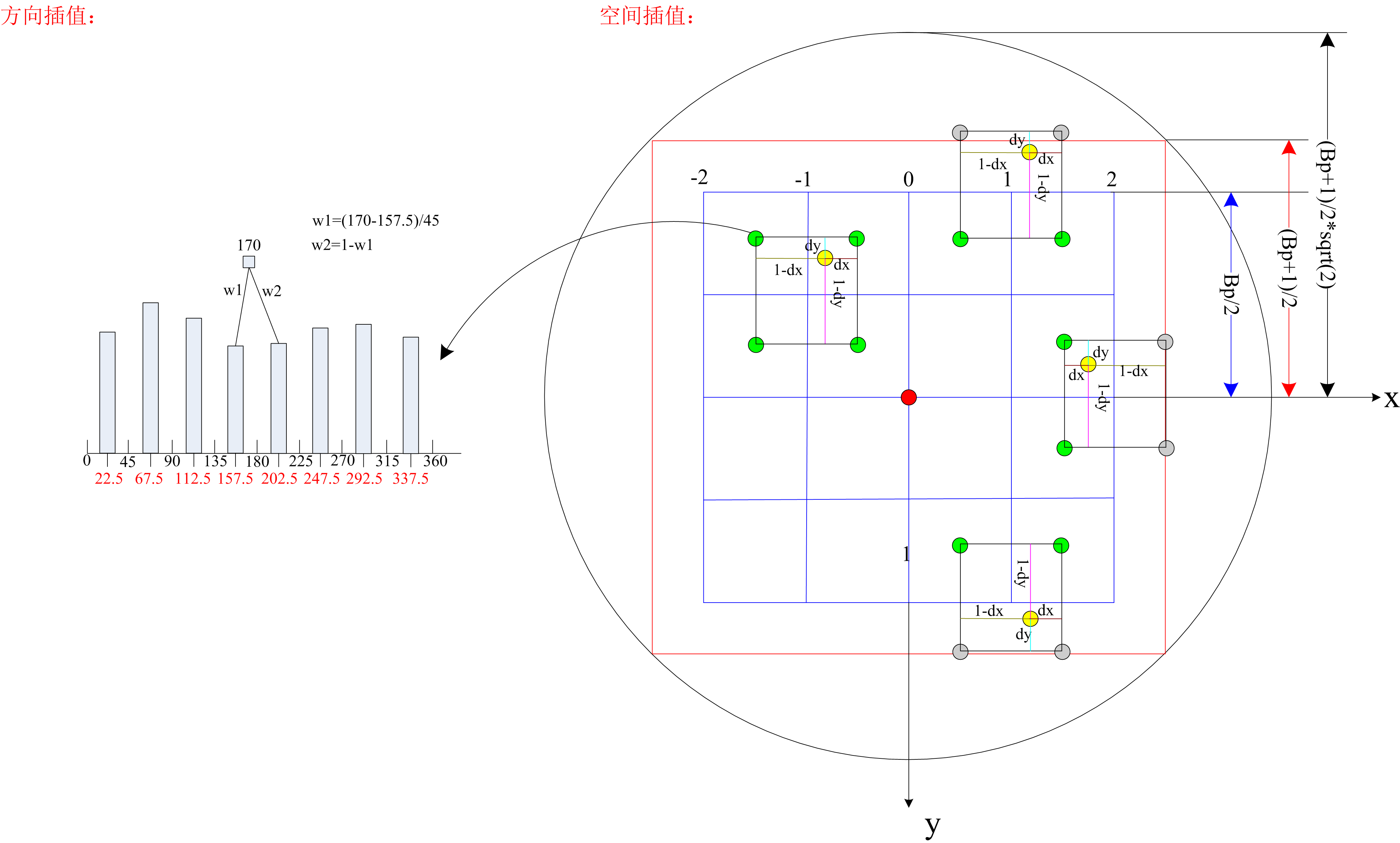
上图，空间插值图有误，下图为修改后

其中dx,dy是相对于黄色点左上角中心（绿色）的距离。

VL_EXPORT
void
vl_sift_calc_keypoint_descriptor (VlSiftFilt *f,
                                  vl_sift_pix *descr,
                                  VlSiftKeypoint const* k,
                                  double angle0)
{
  /*
     The SIFT descriptor is a three dimensional histogram of the
     position and orientation of the gradient.  There are NBP bins for
     each spatial dimension and NBO bins for the orientation dimension,
     for a total of NBP x NBP x NBO bins.

     The support of each spatial bin has an extension of SBP = 3sigma
     pixels, where sigma is the scale of the keypoint.  Thus all the
     bins together have a support SBP x NBP pixels wide. Since
     weighting and interpolation of pixel is used, the support extends
     by another half bin. Therefore, the support is a square window of
     SBP x (NBP + 1) pixels. Finally, since the patch can be
     arbitrarily rotated, we need to consider a window 2W += sqrt(2) x
     SBP x (NBP + 1) pixels wide.
  */

  double const magnif      = f-> magnif ;//3，放大倍数m

  double       xper        = pow (2.0, f->o_cur) ;//步长，针对原图像为250,250的话，如果当前的octave是0，则步长为1，如果octave=1,则步长为2,就是遍历“原图像大小”（不是原图像）的步长

  int          w           = f-> octave_width ;//250
  int          h           = f-> octave_height ;//250
  int const    xo          = 2 ;         /* x-stride *///其将梯度和方向封装在一个数组中，两两间隔，所以步长为2
  int const    yo          = 2 * w ;     /* y-stride */
  int const    so          = 2 * w * h ; /* s-stride *///遍历下一个高斯尺度图像s的步长
  double       x           = k-> x     / xper ;//关键点的位置
  double       y           = k-> y     / xper ;
  double       sigma       = k-> sigma / xper ;//当前的高斯尺度图像对应的尺度，我设置的参数为1.6（针对已知关键点，求描述子的情况）

  int          xi          = (int) (x + 0.5) ;
  int          yi          = (int) (y + 0.5) ;
  int          si          = k-> is ;//有可能是高斯差分对应的索引

  double const st0         = sin (angle0) ;//pi/2-传入的角度pi/8,这里的angle0应该是夹角。
  double const ct0         = cos (angle0) ;
  double const SBP         = magnif * sigma + VL_EPSILON_D ;//m*\sigma 即1个bin的像素大小
  int    const W           = floor
    (sqrt(2.0) * SBP * (NBP + 1) / 2.0 + 0.5) ;//窗口的半径，这里为17，即$\sigma \frac{B_p+1}{2}{\sqrt{2}$,也就是图中外接圆的半径

  int const binto = 1 ;          /* bin theta-stride *///存储的方向bin步长
  int const binyo = NBO * NBP ;  /* bin y-stride *///8*4
  int const binxo = NBO ;        /* bin x-stride *///8

  int bin, dxi, dyi ;
  vl_sift_pix const *pt ;
  vl_sift_pix       *dpt ;

  /* check bounds *///检测边界
  if(k->o  != f->o_cur        ||
     xi    <  0               ||
     xi    >= w               ||
     yi    <  0               ||
     yi    >= h -    1        ||
     si    <  f->s_min + 1    || //0<=si<=2
     si    >  f->s_max - 2     )
    return ;

  /* synchronize gradient buffer *///计算当前octave下，关键点所在的三个尺度(s0,s1,s2)图像上的梯度。问题来了，梯度的计算不是在旋转到主方向在计算吗？
  update_gradient (f) ;

  /* VL_PRINTF("W = %d ; magnif = %g ; SBP = %g\n", W,magnif,SBP) ; */

  /* clear descriptor */
  memset (descr, 0, sizeof(vl_sift_pix) * NBO*NBP*NBP) ;//为描述子分配空间，大小为8*4*4=128，descr描述子的首地址

  /* Center the scale space and the descriptor on the current keypoint.//
   * Note that dpt is pointing to the bin of center (SBP/2,SBP/2,0).
   */
  pt  = f->grad + xi*xo + yi*yo + (si - f->s_min - 1)*so ;//指向关键点处梯度的指针
  dpt = descr + (NBP/2) * binyo + (NBP/2) * binxo ;//指向了描述子的中心，（即直方图的统计中心）binyo表示一行空间bin包括了方向bin，即y_0_即4*8。

#undef atd //at已知dbinx,dbiny,dbint定位其元素值在数组中的位置
#define atd(dbinx,dbiny,dbint) *(dpt + (dbint)*binto + (dbiny)*binyo + (dbinx)*binxo)

  /*
   * Process pixels in the intersection of the image rectangle
   * (1,1)-(M-1,N-1) and the keypoint bounding box.
   */
   //处理边框[-17 17]中的每一个像素
  for(dyi =  VL_MAX (- W, 1 - yi    ) ;
      dyi <= VL_MIN (+ W, h - yi - 2) ; ++ dyi) {

    for(dxi =  VL_MAX (- W, 1 - xi    ) ;
        dxi <= VL_MIN (+ W, w - xi - 2) ; ++ dxi) {

      /* retrieve *///pt指向了关键点处的梯度指针
      vl_sift_pix mod   = *( pt + dxi*xo + dyi*yo + 0 ) ;//梯度
      vl_sift_pix angle = *( pt + dxi*xo + dyi*yo + 1 ) ;//角度//梯度和角度存储在同一个数组中，相互间隔，所以+1就可以遍历到
      vl_sift_pix theta = vl_mod_2pi_f (angle - angle0) ;//如果angle0为主方向的化，angle-angle0相当于该像素的方向与主方向之间的夹角或者差值

      /* fractional displacement */ 关键点离散像素位置和精确位置的偏移
      vl_sift_pix dx = xi + dxi - x;
      vl_sift_pix dy = yi + dyi - y;

      /* get the displacement normalized w.r.t. the keypoint,关于方向和扩展进行标准化，即除以SBP，表示转换为以1bin为单位，即转换到1bin为单位的衡量空间,方向：theta/(2pi/8),角度也是以45bin长为单位，只是换成了弧度制。
         orientation and extension */
      vl_sift_pix nx = ( ct0 * dx + st0 * dy) / SBP ;
      vl_sift_pix ny = (-st0 * dx + ct0 * dy) / SBP ;
      vl_sift_pix nt = NBO * theta / (2 * VL_PI) ;

      /* Get the Gaussian weight of the sample. The Gaussian window
       * has a standard deviation equal to NBP/2. Note that dx and dy
       * are in the normalized frame, so that -NBP/2 <= dx <=
       * NBP/2. */
      vl_sift_pix const wsigma = f->windowSize ;//2,即NBP的一半
      vl_sift_pix win = fast_expn
        ((nx*nx + ny*ny)/(2.0 * wsigma * wsigma)) ;//高斯加权，采用的是标准化到1bin为单位的空间，

      /* The sample will be distributed in 8 adjacent bins.
      //以空间插值图中最左边的黄色像素为例，其大约的位置为(nx,ny)=(-0.75,-1.35), theta=pi/4,nt=0.617那么
      //binx=floor(-0.75-0.5)=-2;左上角的点
      //biny=floor(-1.35-0.5)=-2;左上角的点，
      //bint=1;弧度
      //rbinx=-0.75-(-2+0.5)=-0.75+1.5=0.75;//其中(-2+0.5)定位(-2,-2)对应的bin的中心的x坐标。-0.75-(-2+0.5)表示黄色的点的x坐标到bin的中心点的x坐标之间的距离。
      //rbiny=-1.35-(-2+0.5)=-1.35+0.5=0.15;//同上，(-2+0.5)定位(-2,-2)对应的bin的中心的y坐标，-1.35-(-2+0.5)表示黄色的点的y坐标到bin的中心点的y坐标的距离。
      //rbint=0.617-1=0.383
      //我们知道黄色点所在的bin的中心（蓝色点）的坐标为：(-0.5,-1.5)，则dx=0.25,dy=0.15.
         We start from the ``lower-left'' bin. */ 
      int         binx = (int)vl_floor_f (nx - 0.5) ;
      int         biny = (int)vl_floor_f (ny - 0.5) ;
      int         bint = (int)vl_floor_f (nt) ;
      vl_sift_pix rbinx = nx - (binx + 0.5) ;
      vl_sift_pix rbiny = ny - (biny + 0.5) ;
      vl_sift_pix rbint = nt - bint ;
      int         dbinx ;
      int         dbiny ;
      int         dbint ;

      /* Distribute the current sample into the 8 adjacent bins*/
      //例如空间插值图中，最左边的黄色点，其binx指向(-2,-2)所在的左上角的bin，那么binx+dbinx=binx+0,则表示还是指向该bin,而binx+dbinx=binx+1,则表示指向的黄色点所在的bin，对于binxy同理。再比如，最右边的黄色的点，计算的binx值应该是它所在的bin...
      for(dbinx = 0 ; dbinx < 2 ; ++dbinx) {
        for(dbiny = 0 ; dbiny < 2 ; ++dbiny) {
          for(dbint = 0 ; dbint < 2 ; ++dbint) {

            if (binx + dbinx >= - (NBP/2) &&
                binx + dbinx <    (NBP/2) &&
                biny + dbiny >= - (NBP/2) &&
                biny + dbiny <    (NBP/2) ) {
              vl_sift_pix weight = win
                * mod
                * vl_abs_f (1 - dbinx - rbinx)
                * vl_abs_f (1 - dbiny - rbiny)
                * vl_abs_f (1 - dbint - rbint) ;

              atd(binx+dbinx, biny+dbiny, (bint+dbint) % NBO) += weight ;//数组下标的离散。例如a[-2]就不是当前指针a，向前移动两步。
            }
          }
        }
      }
    }
  }

  /* Standard SIFT descriptors are normalized, truncated and normalized again */
  if(1) {

    /* Normalize the histogram to L2 unit length. */
    //descr描述子的首地址，descr+NBO*NBP*NBP描述子的尾地址
    vl_sift_pix norm = normalize_histogram (descr, descr + NBO*NBP*NBP) ;

    /* Set the descriptor to zero if it is lower than our norm_threshold *///我们这里norma_thresh=0,norm为258
    if(f-> norm_thresh && norm < f-> norm_thresh) {
        for(bin = 0; bin < NBO*NBP*NBP ; ++ bin)
            descr [bin] = 0;
    }
    else {

      /* Truncate at 0.2. */
      //不能超过0.2
      for(bin = 0; bin < NBO*NBP*NBP ; ++ bin) {
        if (descr [bin] > 0.2) descr [bin] = 0.2;
      }

      /* Normalize again. */再次进行标准化
      normalize_histogram (descr, descr + NBO*NBP*NBP) ;
    }
  }

}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186

上面的代码给出加权的计算公式：

vl_sift_pix weight = win
                * mod
                * vl_abs_f (1 - dbinx - rbinx)
                * vl_abs_f (1 - dbiny - rbiny)
                * vl_abs_f (1 - dbint - rbint) ;
1
2
3
4
5

其中：

$$\begin{equation} \begin{aligned} \mathrm{win}=&e^{-{\frac{(x^2+y^2)}{2\sigma_w^2}}},\sigma_w=Bp/2=2\\ \mathrm{mod}=&梯度幅值\\ \mathrm{rbinx},=&dx,\mathrm{rbiny}=dy,其中0 \leq dx \leq 0.5,0 \leq dy \leq 0.5，单位为1bin\\ \mathrm{dbinx},\mathrm{dbiny}\in & \{0,1\}，当0时为:1-dx,当1时为:dx,以此类推... \end{aligned} \end{equation}$$
所以最后的公式为(为了书写的美观，将 $dx$写为 $d_x$， $dy,do$类似)：

$$\begin{equation} \begin{aligned} \mathrm{w}=|grad(I_{\sigma}(x_0,y_0)|\cdot & e^{-\frac{(x^2+y^2)}{2\sigma_w^2}}\cdot (1-d_x)^{1-i} d_x^i \cdot(1-d_y)^{1-j}d_y^j \cdot(1-d_o)^{1-k} d_o^k \end{aligned} \end{equation}$$
其中:$i,j,k \in \{0,1\},\sigma$是当前关键点所在的图像尺度。$x_0,y_0$的单位像素;x,y的单位为1bin(空间bin,范围为[-2,2]，x轴方向,长度为4,y轴方向长度为4，1bin=$3\sigma$像素；$d_x,d_y$的单位也是1bin；$d_o$的单位为1bin（但是是方向bin，bin的范围为[0,8],长度为8，1bin=$\frac{2\pi}{8}=0.25\pi弧度$）。从$x_0.y_0$到$x,y$通过仿射映射和坐标单位换算得到。

VLFeat代码中给出图像旋转后的坐标的计算公式为:
$$\begin{equation} \begin{pmatrix} x'\\ y' \end{pmatrix}=\begin{pmatrix} cos \theta & sin \theta\\ -sin \theta& cos \theta \end{pmatrix} \begin{pmatrix} x\\ y \end{pmatrix}(x,y \in [-r,r]) \end{equation}$$
D.Lowe’s sift实现中的计算公式：
$$\begin{equation} \begin{pmatrix} x'\\ y' \end{pmatrix}=\begin{pmatrix} cos \theta & -sin \theta\\ sin \theta& cos \theta \end{pmatrix} \begin{pmatrix} x\\ y \end{pmatrix}(x,y \in [-r,r]) \end{equation}$$
之所有会出现上面的差别，是因为选用了不同的坐标系和角度的旋转规则：
下图给出VLFeat实现的约定规则和D.Lowes实现的约定规则：

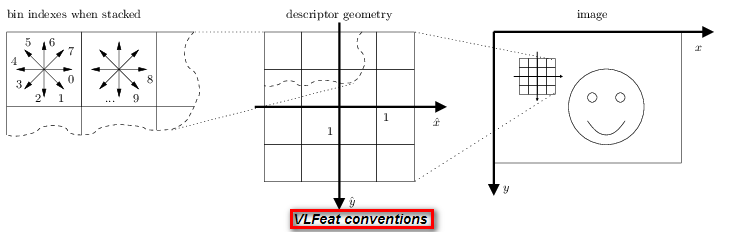
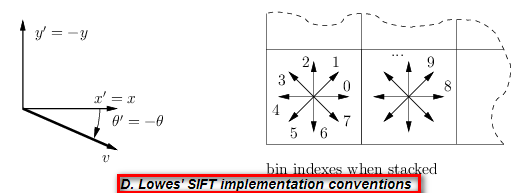
其中VLFeat的代码中，对于输入主方向，例如为$-\pi/8$,其进行了下面的操作：

 angles [0] = VL_PI / 2 - ikeys [4 * i + 3] ;%ikeys[4*i+3]=-pi/8
1

即：

$$\theta_0=\frac{\pi}{2}-(-\frac{\pi}{8})$$
下图给出了详细操作的解释：

坐标的虚线框内描述了理论上的计算过程，右边虚线框内描述了实际的计算过程，因为Matlab矩阵的存储方式是按列存储的，而c是按行存储的，所以在C中处理的图像其实是实际图像的转置。

sift描述子主方向的计算

这里给出了代码：

VL_EXPORT
int
vl_sift_calc_keypoint_orientations (VlSiftFilt *f,
                                    double angles [4],
                                    VlSiftKeypoint const *k)
{
  double const winf   = 1.5 ;
  double       xper   = pow (2.0, f->o_cur) ;

  int          w      = f-> octave_width ;
  int          h      = f-> octave_height ;
  int const    xo     = 2 ;         /* x-stride */
  int const    yo     = 2 * w ;     /* y-stride */
  int const    so     = 2 * w * h ; /* s-stride */
  double       x      = k-> x     / xper ;
  double       y      = k-> y     / xper ;
  double       sigma  = k-> sigma / xper ;

  int          xi     = (int) (x + 0.5) ;
  int          yi     = (int) (y + 0.5) ;
  int          si     = k-> is ;

  double const sigmaw = winf * sigma ;
  int          W      = VL_MAX(floor (3.0 * sigmaw), 1) ;

  int          nangles= 0 ;

  enum {nbins = 36} ;

  double hist [nbins], maxh ;
  vl_sift_pix const * pt ;
  int xs, ys, iter, i ;

  /* skip if the keypoint octave is not current */
  if(k->o != f->o_cur)
    return 0 ;

  /* skip the keypoint if it is out of bounds */
  if(xi < 0            ||
     xi > w - 1        ||
     yi < 0            ||
     yi > h - 1        ||
     si < f->s_min + 1 ||
     si > f->s_max - 2  ) {
    return 0 ;
  }

  /* make gradient up to date */
  update_gradient (f) ;

  /* clear histogram */
  memset (hist, 0, sizeof(double) * nbins) ;

  /* compute orientation histogram */
  pt = f-> grad + xo*xi + yo*yi + so*(si - f->s_min - 1) ;

#undef  at
#define at(dx,dy) (*(pt + xo * (dx) + yo * (dy)))

  for(ys  =  VL_MAX (- W,       - yi) ;
      ys <=  VL_MIN (+ W, h - 1 - yi) ; ++ys) {

    for(xs  = VL_MAX (- W,       - xi) ;
        xs <= VL_MIN (+ W, w - 1 - xi) ; ++xs) {


      double dx = (double)(xi + xs) - x;
      double dy = (double)(yi + ys) - y;
      double r2 = dx*dx + dy*dy ;
      double wgt, mod, ang, fbin ;

      /* limit to a circular window */
      if (r2 >= W*W + 0.6) continue ;

      wgt  = fast_expn (r2 / (2*sigmaw*sigmaw)) ;
      mod  = *(pt + xs*xo + ys*yo    ) ;
      ang  = *(pt + xs*xo + ys*yo + 1) ;
      fbin = nbins * ang / (2 * VL_PI) ;

#if defined(VL_SIFT_BILINEAR_ORIENTATIONS)
      {
        int bin = (int) vl_floor_d (fbin - 0.5) ;
        double rbin = fbin - bin - 0.5 ;
        hist [(bin + nbins) % nbins] += (1 - rbin) * mod * wgt ;
        hist [(bin + 1    ) % nbins] += (    rbin) * mod * wgt ;
      }
#else
      {
        int    bin  = vl_floor_d (fbin) ;
        bin = vl_floor_d (nbins * ang / (2*VL_PI)) ;
        hist [(bin) % nbins] += mod * wgt ;
      }
#endif

    } /* for xs */
  } /* for ys */

  /* smooth histogram */
  for (iter = 0; iter < 6; iter ++) {
    double prev  = hist [nbins - 1] ;
    double first = hist [0] ;
    int i ;
    for (i = 0; i < nbins - 1; i++) {
      double newh = (prev + hist[i] + hist[(i+1) % nbins]) / 3.0;
      prev = hist[i] ;
      hist[i] = newh ;
    }
    hist[i] = (prev + hist[i] + first) / 3.0 ;
  }

  /* find the histogram maximum */
  maxh = 0 ;
  for (i = 0 ; i < nbins ; ++i)
    maxh = VL_MAX (maxh, hist [i]) ;

  /* find peaks within 80% from max */
  nangles = 0 ;
  for(i = 0 ; i < nbins ; ++i) {
    double h0 = hist [i] ;
    double hm = hist [(i - 1 + nbins) % nbins] ;
    double hp = hist [(i + 1 + nbins) % nbins] ;

    /* is this a peak? */
    if (h0 > 0.8*maxh && h0 > hm && h0 > hp) {

      /* quadratic interpolation */
      double di = - 0.5 * (hp - hm) / (hp + hm - 2 * h0) ;
      double th = 2 * VL_PI * (i + di + 0.5) / nbins ;
      angles [ nangles++ ] = th ;
      if( nangles == 4 )
        goto enough_angles ;
    }
  }
 enough_angles:
  return nangles ;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137

计算描述子方向的窗口大小为:$w=\max(\left \lfloor3*(\mathrm{win}_f*\sigma)\right \rfloor,1)$，其中$\mathrm{win}_f=1.5，\sigma$为当前关键点所在的尺度，本例中w=7,即$\sigma$取1.6。其将360度的方向划成了36个bin(为了确定更精确的方向）。这里是为了计算主方向，在尺度图像上进行梯度，而不需要仿射变换。

高斯金字塔图像

在Vlfeat的vl_sift.cpp中（为了使用opencv,mexopencv,我们将其改为了cpp文件）中添加如下的代码，输出保存高斯图像金字塔。

      if (first) {
        err   = vl_sift_process_first_octave (filt, data) ;
        //add my code,out[2]对图像进行输出
        int smax=4;
        int smin=-1;
        int ns=smax-smin+1;
        vl_sift_pix *oct0 = filt->octave ;
        int o=vl_sift_get_octave_index (filt);
        Mat mat0(M*N,ns,CV_8UC1);
        for(int k=0;k<ns;k++)
        {
            int st=k*M*N;
            for(int jj=0;jj<N;jj++)//N表示列数
                for(int ii=0;ii<M;ii++)//M表示行数
                    mat0.at<uchar>(ii+jj*N,k)=(uchar)oct0[ii+jj*N+st];
        }
        out[o+2]=MxArray(mat0);
        first = 0 ;
      } else {
        err   = vl_sift_process_next_octave  (filt) ;
        //add my code,out[2]对图像进行输出
        int smax=4;
        int smin=-1;
        int ns=smax-smin+1;
        vl_sift_pix *oct0 = filt->octave ;
        int o=vl_sift_get_octave_index (filt);
        int m=M/(pow(2.0,o));
        int n=N/(pow(2.0,o));
        Mat mat0(m*n,ns,CV_8UC1);
        for(int k=0;k<ns;k++)
        {
            int st=k*m*n;
            for(int jj=0;jj<n;jj++)//N表示列数
                for(int ii=0;ii<m;ii++)//M表示行数
                    mat0.at<uchar>(ii+jj*n,k)=(uchar)oct0[ii+jj*n+st];
        }
        out[o+2]=MxArray(mat0);

      }
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39

下图给出了，4个octave的第一个s的图像：

下图给出了第一个octave下的6个尺度图像：

VLFeat中计算给定关键点的描述子时间测试

clearvars;close all;
imgPath='E:\data\lfw\imgs\Aaron_Eckhart\Aaron_Eckhart_0001.jpg';
bbox=[63 72 126+63 126+72];
landmark=[34 35; 53 38; 41 86; 75 90; 58 93; 59 87 ;72 40 ;94 43; 48 70; 72 72];
nlandmark=10;
sigma=0.5;
ori=0;
img=imread(imgPath);
img_gray=rgb2gray(img);
I=single(img_gray);
%% 批量处理
tic;
w=bbox(3)-bbox(1)+1;
h=bbox(4)-bbox(2)+1;
fc=zeros(4,w*h);
for i=bbox(1):bbox(3)
    for j=bbox(2):bbox(4)
        fc_t=[i;j;sigma;ori];
        ii=i-bbox(1)+1;
        jj=j-bbox(2)+1;
        fc(:,jj+(ii-1)*w)=fc_t;
    end
end
pre_time=toc;
tic;
[f,d]=vl_sift(I,'frames',fc,'orientations');
sift_time=toc;
disp(['准备关键点所用的时间: ' num2str(pre_time)]);
disp(['计算区域大小为126*126个像素的描述子的时间: ' num2str(sift_time)]);
%% 单个处理
fc2=[63;72;sigma;ori];
tic;
[f2,d2]=vl_sift(I,'frames',fc2,'orientations');
sift_time2=toc;
disp(['计算一个关键点的描述时间: ' num2str(sift_time2)]);
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36

result:

准备关键点所用的时间: 0.024732
计算区域大小为126*126个像素的描述子的时间: 0.59428
计算一个关键点的描述时间: 0.078686
1
2
3

我们发现，VLFeat即使在给定关键点即位置，初始尺度和方向，其也会将所有octave和s计算出。这花费了大量的时间。因此使用时，要对代码进行修改。即只计算指定尺度下的高斯图像的描述子。

关键点描述子的计算，可参考：
http://blog.csdn.net/raby_gyl/article/details/52800106

在图像框架中计算描述子

VLFat使用下面的理论，实现在原图像上进行梯度的计算，然后再经过仿射。而不是在旋转后的图像上进行梯度的计算。
翻译：http://www.vlfeat.org/api/sift.html
为关键点附加一个描述子可以获得相似变换的不变形（或者其他的相似协变帧）。那么将图像投影到标准描述子框架中有消除图像变形的效果。
然而在实际中，在图像框架中很容易计算描述子。我们用带${\hat{}}$表示标准框架，用不带$\hat{}$表示图像框架。假定标准框架和图像框架是仿射相关的：

$$\begin{equation} \mathbf x=A\hat{\mathbf x}+T \begin{bmatrix} c\hat x\\ \hat y \end{bmatrix},\begin{bmatrix} cx\\ y \end{bmatrix} \end{equation}$$
因此可以在图像框架中直接计算所有的量，例如无限分辨率的图像在两个框架中是相关的：
$$\hat I_0(\hat{\mathbf x})=I_0(\mathbf x),\mathbf x=A \hat {\mathbf x}+T$$
尺度 $\hat \sigma$的标准化的图像，与尺度图像是相关的：
$$\hat I_{\hat \sigma}(\hat{\mathbf x})=I_{A \hat \sigma}(\mathbf x),\mathbf x=A\hat {\mathbf x}+T$$
…..略

参考文献：

1.http://www.vlfeat.org/overview/sift.html
2.http://www.vlfeat.org/api/sift.html
3.An open implementation of the SIFT detector and descriptor
sift:
4.http://blog.csdn.net/xiaowei_cqu/article/details/8069548 [小魏的修行路]
5.http://blog.csdn.net/zddblog/article/details/7521424 [zddhub的专栏]
6.http://blog.csdn.net/abcjennifer/article/details/7639681 [Rachel Zhang的专栏]
vlfeat:
7.http://blog.csdn.net/fengbingchun/article/details/50638391 [网络资源是无限的]
8.http://www.cnblogs.com/yao7837005/archive/2012/08/24/2654797.html [一直走下去]
9.http://blog.csdn.net/liguan843607713/article/details/42215965 [Object o]