Monodyee

这个屌丝很懒，什么也没留下！

热门标签

支持向量机SVM在回归问题中的应用：支持向量回归SVR（python代码实现）_支持向量机回归代码

作者：Monodyee | 2024-03-26 05:05:50

踩

支持向量机回归代码

本文摘录自支持向量回归SVR - 数模百科

你玩过放风筝吗？放风筝可有讲究哦，如果你能熟练地控制着那根风筝线，风筝就能在蓝天上自由自在地飞。想象一下，风筝就是你心中追求的那个答案，而风筝线的长短、指向，就像是指引你找到答案的线索。

比如说，你在玩一个猜谜游戏，游戏里给你的提示就像是掌握在手里的风筝线，你得根据这些线索去猜风筝在天空中的具体位置。可是，风筝受风的影响，会不停地在空中变换位置。你的任务就是要依靠手上的这些线索，尽量猜出风筝现在可能在哪儿。

支持向量回归（SVR）就好比是个放风筝的行家里手。首先，他会在脑海中构想出一条完美的理想风筝线，这根线能够让风筝牢牢地定位在一个最佳点上。然后，他允许风筝在这个理想位置周围的一小块区域内自由飘荡，只要风筝不飘出这个区域，他都能接受。他更关注的是那些偏离了这个自由飘荡区域太远的风筝，因为它们脱离了正常的预期范围。

就像一个专注的放风筝人，他会一遍又一遍地调整风筝线的拉力和角度，努力让风筝尽量飞回他心中设想的那个点上。这种不断调整，寻找最合适位置的过程，就是支持向量回归的主旨所在。

再举个例子。

你还记得咱们小时候玩的“猜数字”游戏吗？我就随便心里想一个1到10之间的数，然后你来猜。咱们玩的时候，如果你猜的数字不对，我会提示你是猜大了还是猜小了，你根据提示再接着猜，直到猜中为止。

但如果我们把规则改一改，就有点意思了。你还是猜我心里的数字，可这次我不再告诉你猜大了还是小了，我只会告诉你你猜的和我心里数的差了多少。比如说，假设我心里想的是数字3，你如果猜了个5，我就跟你说：“差了2”。你猜的越接近，我就认为你猜得越好。

这个改头换面的新游戏，其实和一个数学上的东西挺像，那就是支持向量回归，简称SVR。你可以把SVR想象成一个特别会玩儿“猜数字”游戏的高手。它不靠我告诉你猜大了还是小了，而是通过观察你和正确答案的差距，来不断调整自己的猜测。它的目的就是要把这个差距弄得尽可能小，这个过程就叫做“最优化”。

所以呢，即便我们没直接把正确答案告诉SVR，它也能通过自己聪明的方法，一步步逼近真正的答案，最后猜出一个相当准确的数来。这就是SVR这个数学工具的聪明之处。

定义与详解

定义

支持向量回归（Support Vector Regression，SVR）是支持向量机（SVM）在回归问题上的应用。SVR用于预测一个连续的输出变量，相比于分类任务的SVM，其主要区别在于构造的不再是一个最大间隔的超平面，而是构造一个与目标函数值间隔在一定范围内（ε-insensitive）的最小超平面。

与SVM一样，SVR也可以通过引入核函数来解决非线性问题。通过核技巧，SVR能将原始特征空间映射为更高维的特征空间，以便找到在更高维空间中的线性回归模型。

直观理解，SVR的目标是找到一个函数 $f(x_i)$ ，尽可能接近所有样本点，但忽略掉位于ε-tube（由训练误差 ε 定义）之内的预测误差。其数学定义涉及到解决以下优化问题：

SVR的优化问题可以表示为：

$\min_{w,b,\xi_i, \hat{\xi_i}}\frac{1}{2}||w||^2+C\sum_{i=1}^{m}(\xi_i+\hat{\xi_i}),$

进行下列约束：

$\ s.t. \ f(x_i)-y_i\leq\varepsilon+\xi_i ,\\ y_i-f(x_i) \leq \varepsilon+\hat{\xi_i},\\ \xi_i, \hat{\xi_i}\geq0, \ i=1,2,\ldots,m.$

这里 w 和 b 是预测函数的参数， $f(x_i)=wx_i+b$ ； $\xi_i$ 和 $\hat{\xi_i}$ 是正的缓冲变量，用于处理不在ε-tube内的样本；C 是用于控制模型复杂度与训练误差之间平衡的正则化参数； $\varepsilon$ 是我们希望预测函数逼近目标值的精度。

解法

引入拉格朗日乘子，这个问题可以通过求解对偶问题来解决，我们最后得到的优化问题是：

$\max_{\alpha, \hat{\alpha}} \sum_{i=1}^{m} y_i(\hat{\alpha_i}-\alpha_i) -\varepsilon \sum_{i=1}^{m} (\hat{\alpha_i}+\alpha_i) -\frac{1}{2}\sum _{i,j=1}^{m} (\hat{\alpha_i}-\alpha_i)(\hat{\alpha_j}-\alpha_j) x_i^T x_j ,$

限制为：

$\sum_{i=1}^{m} (\hat{\alpha_i}-\alpha_i) =0, \quad \quad 0\leq \hat{\alpha_i},\alpha_i \leq C.$

求解完上述问题，得到每个样本对应的 $\alpha_i$ 和 $\hat{\alpha_i}$ 后，我们可以通过下式计算对新样本 x 的预测值：

$f(x)=\sum_{i=1}^{m}{(\hat{\alpha_i}-\alpha_i)x_i^T x+b}.$

在SVR中，仅当样本点不落在 $\varepsilon$ 间的隔带中时，相应的 $\alpha_i$ 和 $\hat{\alpha_i}$ 才能取非零值，这些样本点被称为“支持向量”。这就表示，SVR的解只与部分训练样本（支持向量）有关，这称为SVR的稀疏性。

同样，SVR也可以引入核函数 $K(x_i, x_j)=\phi(x_i)^T \phi(x_j)$ 来处理非线性问题，从而获得非线性的SVR模型。最后的模型则为：

$f(x)=\sum_{i=1}^{m}{(\hat{\alpha_i}-\alpha_i)K(x_i, x)+b}.$

SVR和一般线性回归的区别

SVR通过引入间隔带和松弛变量, 对于在间隔带之内的数据点, 即预测值与真实值的差的绝对值小于设定的阈值 ε，其损失是0, 不计入损失函数的计算。只有当预测值与真实值的差距的绝对值大于 ε 时, 才会计算损失，而且损失是线性的。这也就是为什么SVR也被称为ε-不敏感损失函数。相比之下，一般的线性回归模型在损失函数的计算上没有这样的间隔带概念，只要预测值与真实值有偏差，无论偏差大小，都会计入损失，其损失函数通常是预测值与真实值差的平方。
SVR的优化目标是最大化间隔带的宽度与最小化总损失。这就意味着SVR试图找到一个能使大部分数据点都处在间隔带之内的函数，而且对于位于间隔带之外的数据点，尽量让其离间隔带越近越好。一般线性回归的优化目标是最小化所有数据点的损失总和，通常采用梯度下降算法来求解。线性回归更注重所有数据点的拟合效果，而不是提供一种机制来忽略那些可能的噪声点。
利用SVR，我们可以使用核函数来处理非线性的问题，而一般的线性回归没有这样的功能。同时，SVR的最优解只依赖于部分数据（支持向量），使得模型具有稀疏性，从而提高计算效率，在大规模数据集上比线性回归有优势。

代码


import matplotlib.pyplot as plt
from sklearn.svm import SVR
from sklearn import datasets
from sklearn.model_selection import train_test_split, GridSearchCV
from sklearn.preprocessing import StandardScaler
from sklearn.metrics import mean_squared_error, r2_score
plt.rcParams['font.sans-serif'] = ['SimHei']
import numpy as np
 
# 加载波士顿房价数据集
boston = datasets.load_boston()
 
# 切分训练集和测试集
X_train, X_test, y_train, y_test = train_test_split(boston.data, boston.target, test_size=0.2, random_state=42)
 
# 数据标准化
scaler_x = StandardScaler()
X_train_std = scaler_x.fit_transform(X_train)
X_test_std = scaler_x.transform(X_test)
 
scaler_y = StandardScaler()
y_train_std = scaler_y.fit_transform(y_train.reshape(-1,1)).ravel()
y_test_std = scaler_y.transform(y_test.reshape(-1,1)).ravel()
 
# 设置待测试的参数
param_grid = {"C": [1e0, 1e1, 1e2, 1e3],
              "gamma": np.logspace(-2, 2, 5)}
 
# 利用GridSearchCV寻找最优参数
model = GridSearchCV(SVR(kernel='rbf', gamma=0.1), cv=5, param_grid=param_grid)
model.fit(X_train_std, y_train_std)
 
# 打印最优参数
print("The best parameters are %s with a score of %0.2f" % (model.best_params_, model.best_score_))
 
# 做预测
y_pred = model.predict(X_test_std)
 
# 打印R2分数和均方误差
print('R2 score: ', r2_score(y_test_std, y_pred))
print('Mean squared error: ', mean_squared_error(y_test_std, y_pred))
 
# 绘图
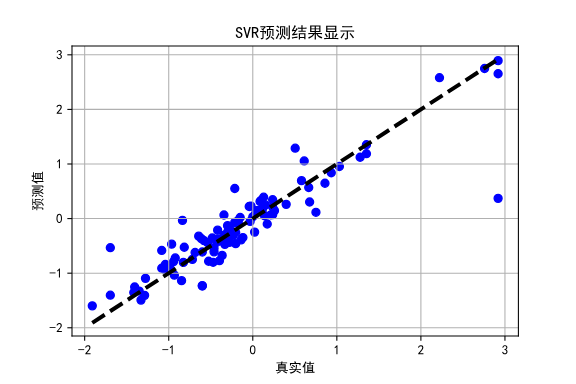
plt.scatter(y_test_std, y_pred, color='blue')
plt.plot([y_test_std.min(), y_test_std.max()], [y_test_std.min(), y_test_std.max()], 'k--', lw=3)
plt.xlabel('真实值')
plt.ylabel('预测值')
plt.title('SVR预测结果显示')
plt.grid()
plt.show()

这段代码的工作如下：

加载波士顿房价数据集。
将数据集分为训练集和测试集，测试集的比例为20%，并设置起始的随机种子。
对特征值和目标值进行标准化处理。
设置支持向量回归（SVR）模型待测试的参数。
利用网格搜索（GridSearchCV）在给定的参数范围内找到最优的参数。
使用最优参数训练模型。
打印最优参数及其对应的分数。
对测试集进行预测。
计算并打印出预测结果的R2分数（决定系数）和均方误差。
将实际结果和预测结果进行可视化，并绘制出一条对角线表示在预测完全准确时的理想情况。

输出结果：


The best parameters are {'C': 10.0, 'gamma': 0.1} with a score of 0.88
R2 score:  0.8316248029392441
Mean squared error:  0.14213314600372265

#优缺点

优点：

对于非线性问题，可以通过核函数将数据映射到高维度特征空间，处理线性不可分问题。
只依赖少数的“支持向量”，减少了运算量。
可以很好地处理高维数据，无需降维。
对噪声有较好的鲁棒性。

缺点：

对大规模训练样本，计算需要耗费大量时间。
对于核的选择和参数设定需要专业知识。
对于多重共线性数据，效果较差，也就是存在很多相关性强的特征时
对于缺失数据难以处理。

本篇文章来自于数模百科 —— 支持向量回归SVR - 数模百科

数模百科是一个由一群数模爱好者搭建的数学建模知识平台。我们想让大家只通过一个网站，就能解决自己在数学建模上的难题，把搜索和筛选的时间节省下来，投入到真正的学习当中。

我们团队目前正在努力为大家创建最好的信息集合，从用最简单易懂的话语和生动形象的例子帮助大家理解模型，到用科学严谨的语言讲解模型原理，再到提供参考代码。我们努力为数学建模的学习者和参赛者提供一站式学习平台，目前网站已上线，期待大家的反馈。

如果你想和我们的团队成员进行更深入的学习和交流，你可以通过公众号数模百科找到我们，我们会在这里发布更多资讯，也欢迎你来找我们唠嗑。

声明：本文内容由网友自发贡献，不代表【wpsshop博客】立场，版权归原作者所有，本站不承担相应法律责任。如您发现有侵权的内容，请联系我们。转载请注明出处：https://www.wpsshop.cn/w/Monodyee/article/detail/314811