机器学习（十四）生成对抗网络（GAN）_csdn gan

摘要

生成对抗网络其实是两个网络的组合：生成网络（Generator）负责生成模拟数据；判别网络Discriminator）负责判断输入的数据是真实的还是生成的。生成网络要不断优化自己生成的数据让判别网络判断不出来，判别网络也要优化自己让自己判断得更准确。二者关系形成对抗，因此叫对抗网络。

Abstract

Creating a confrontation network is actually a combination of two networks: generating the network (generator) responsible for generating simulated data; The discriminator network discriminator is responsible for judging whether the input data is real or generated. The network of generating the network is not able to determine the network, and the network also needs to optimize itself to make it more accurate. The relationship is against the Internet.

1 GAN基本概念

1.1 GAN的定义？

​ 生成对抗网络(GAN, Generative adversarial network)自从2014年被Ian Goodfellow提出以来，掀起来了一股研究热潮。GAN由生成器和判别器组成，生成器负责生成样本，判别器负责判断生成器生成的样本是否为真。生成器要尽可能迷惑判别器，而判别器要尽可能区分生成器生成的样本和真实样本。
​ 在GAN的原作中，作者将生成器比喻为印假钞票的犯罪分子，判别器则类比为警察。犯罪分子努力让钞票看起来逼真，警察则不断提升对于假钞的辨识能力。二者互相博弈，随着时间的进行，都会越来越强。那么类比于图像生成任务，生成器不断生成尽可能逼真的假图像。判别器则判断图像是否是真实的图像，还是生成的图像，二者不断博弈优化。最终生成器生成的图像使得判别器完全无法判别真假。

1.2 GAN的形式化表达

​ 上述例子只是简要介绍了一下GAN的思想，下面对于GAN做一个形式化的，更加具体的定义。通常情况下，无论是生成器还是判别器，我们都可以用神经网络来实现。那么，我们可以把通俗化的定义用下面这个模型来表示：

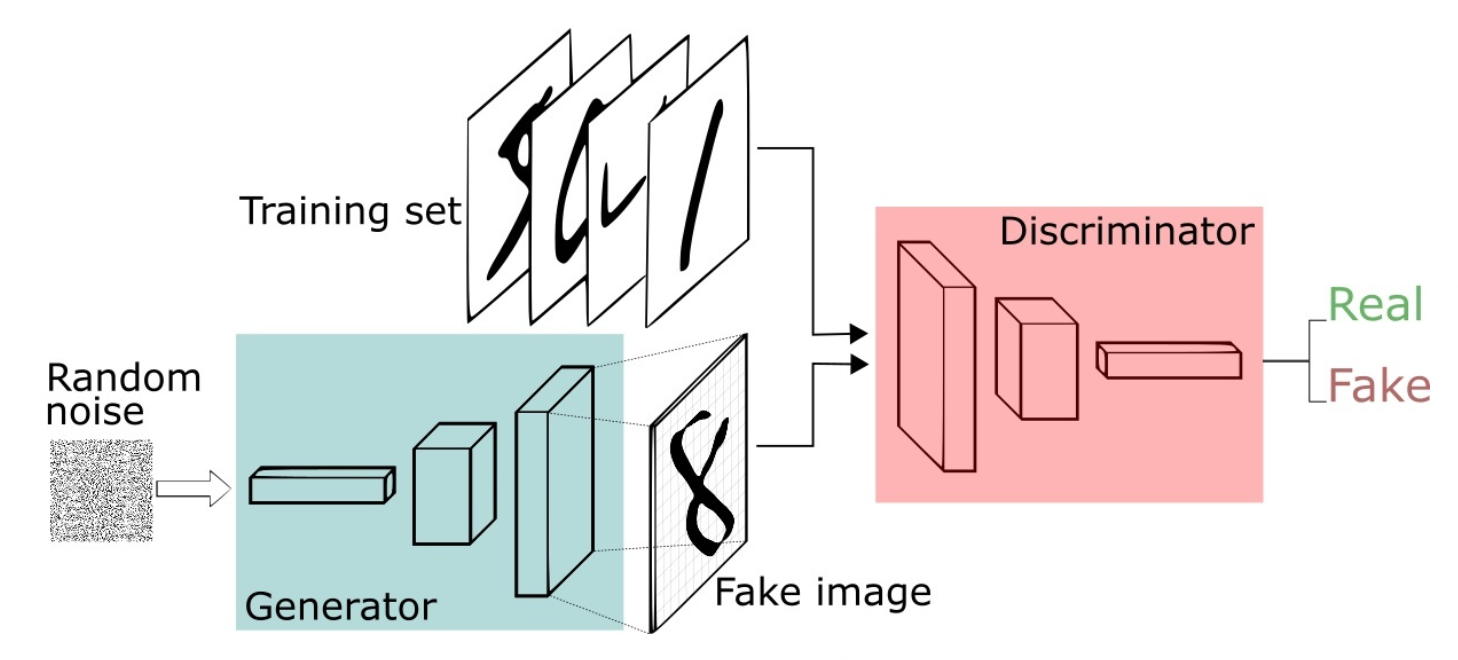
上述模型左边是生成器G，其输入是$z$，对于原始的GAN，$z$是由高斯分布随机采样得到的噪声。噪声$z$通过生成器得到了生成的假样本。

​ 生成的假样本与真实样本放到一起，被随机抽取送入到判别器D，由判别器去区分输入的样本是生成的假样本还是真实的样本。整个过程简单明了，生成对抗网络中的“生成对抗”主要体现在生成器和判别器之间的对抗。

1.3 GAN的目标函数是什么？

​ 对于上述神经网络模型，如果想要学习其参数，首先需要一个目标函数。GAN的目标函数定义如下：

$$\underset{G}{\min }\underset{D}{\max }V(D,G)=\mathrm{E}x\sim pdata(x)[\log D(x)]+{\mathrm{E}}_{z\sim p_z(z)}[\log (1-D(G(z)))]$$​ 这个目标函数可以分为两个部分来理解：

​ 第一部分：判别器的优化通过$\underset{D}{\max }V(D,G)$实现，$V(D,G)$为判别器的目标函数，其第一项$\mathrm{E}x\sim pdata(x)[\log D(x)]$表示对于从真实数据分布 中采用的样本 ,其被判别器判定为真实样本概率的数学期望。对于真实数据分布 中采样的样本，其预测为正样本的概率当然是越接近1越好。因此希望最大化这一项。第二项${\mathrm{E}}_{z\sim p_z(z)}[\log (1-D(G(z)))]$表示：对于从噪声$P_z(z)$分布当中采样得到的样本，经过生成器生成之后得到的生成图片，然后送入判别器，其预测概率的负对数的期望，这个值自然是越大越好，这个值越大， 越接近0，也就代表判别器越好。

​ 第二部分：生成器的优化通过$\underset{G}{\min }(\underset{D}{\max }V(D,G))$来实现。注意，生成器的目标不是$\underset{G}{\min }V(D,G)$，即生成器不是最小化判别器的目标函数，二是最小化判别器目标函数的最大值，判别器目标函数的最大值代表的是真实数据分布与生成数据分布的JS散度(详情可以参阅附录的推导)，JS散度可以度量分布的相似性，两个分布越接近，JS散度越小。

1.4 GAN的目标函数和交叉熵有什么区别？

判别器目标函数写成离散形式即为:

​ 可以看出，这个目标函数和交叉熵是一致的，即判别器的目标是最小化交叉熵损失，生成器的目标是最小化生成数据分布和真实数据分布的JS散度。

1.5 GAN的Loss为什么降不下去？

对于很多GAN的初学者在实践过程中可能会纳闷，为什么GAN的Loss一直降不下去。GAN到底什么时候才算收敛？其实，作为一个训练良好的GAN，其Loss就是降不下去的。衡量GAN是否训练好了，只能由人肉眼去看生成的图片质量是否好。不过，对于没有一个很好的评价是否收敛指标的问题，也有许多学者做了一些研究，后文提及的WGAN就提出了一种新的Loss设计方式，较好的解决了难以判断收敛性的问题。下面我们分析一下GAN的Loss为什么降不下去？​ 对于判别器而言，GAN的Loss如下： $$\underset{G}{\min }\underset{D}{\max }V(D,G)=\mathrm{E}x\sim pdata(x)[\log D(x)]+{\mathrm{E}}_{z\sim p_z(z)}[\log (1-D(G(z)))]$$​ 从$\underset{G}{\min }\underset{D}{\max }V(D,G)$可以看出，生成器和判别器的目的相反，也就是说两个生成器网络和判别器网络互为对抗，此消彼长。不可能Loss一直降到一个收敛的状态。

• 对于生成器，其Loss下降快，很有可能是判别器太弱，导致生成器很轻易的就"愚弄"了判别器。
• 对于判别器，其Loss下降快，意味着判别器很强，判别器很强则说明生成器生成的图像不够逼真，才使得判别器轻易判别，导致Loss下降很快。

1.6 生成式模型、判别式模型的区别？

对于机器学习模型，我们可以根据模型对数据的建模方式将模型分为两大类，生成式模型和判别式模型。如果我们要训练一个关于猫狗分类的模型，对于判别式模型，只需要学习二者差异即可。比如说猫的体型会比狗小一点。而生成式模型则不一样，需要学习猫长什么样，狗长什么样。有了二者的长相以后，再根据长相去区分。具体而言.

• 生成式模型：由数据学习联合概率分布P(X,Y), 然后由P(Y|X)=P(X,Y)/P(X)求出概率分布P(Y|X)作为预测的模型。该方法表示了给定输入X与产生输出Y的生成关系

• 判别式模型：由数据直接学习决策函数Y=f(X)或条件概率分布P(Y|X)作为预测模型，即判别模型。判别方法关心的是对于给定的输入X，应该预测什么样的输出Y。

​ 对于上述两种模型，从文字上理解起来似乎不太直观。我们举个例子来阐述一下，对于性别分类问题，分别用不同的模型来做：

​ 1）如果用生成式模型：可以训练一个模型，学习输入人的特征X和性别Y的关系。比如现在有下面一批数据：

这个数据可以统计得到，即统计人的特征X=0,1….的时候，其类别为Y=0,1的概率。统计得到上述联合概率分布P(X, Y)后，可以学习一个模型，比如让二维高斯分布去拟合上述数据，这样就学习到了X，Y的联合分布。在预测时，如果我们希望给一个输入特征X，预测其类别，则需要通过贝叶斯公式得到条件概率分布才能进行推断：

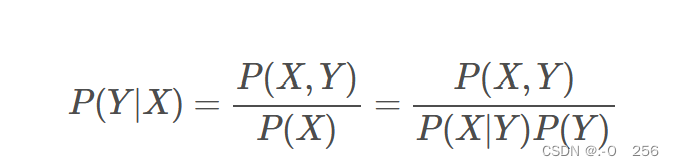
2）如果用判别式模型：可以训练一个模型，输入人的特征X，这些特征包括人的五官，穿衣风格，发型等。输出则是对于性别的判断概率，这个概率服从一个分布，分布的取值只有两个，要么男，要么女，记这个分布为Y。这个过程学习了一个条件概率分布P(Y|X)，即输入特征X的分布已知条件下，Y的概率分布。

​ 显然，从上面的分析可以看出。判别式模型似乎要方便很多，因为生成式模型要学习一个X，Y的联合分布往往需要很多数据，而判别式模型需要的数据则相对少，因为判别式模型更关注输入特征的差异性。不过生成式既然使用了更多数据来生成联合分布，自然也能够提供更多的信息，现在有一个样本（X,Y）,其联合概率P（X,Y）经过计算特别小，那么可以认为这个样本是异常样本。这种模型可以用来做outlier detection。

1.7 什么是mode collapsing?

​ 某个模式(mode)出现大量重复样本，例如： ​ 上图左侧的蓝色五角星表示真实样本空间，黄色的是生成的。生成样本缺乏多样性，存在大量重复。比如上图右侧中，红框里面人物反复出现。

1.8 如何解决mode collapsing？

方法一：针对目标函数的改进方法

​ 为了避免前面提到的由于优化maxmin导致mode跳来跳去的问题，UnrolledGAN采用修改生成器loss来解决。具体而言，UnrolledGAN在更新生成器时更新k次生成器，参考的Loss不是某一次的loss，是判别器后面k次迭代的loss。注意，判别器后面k次迭代不更新自己的参数，只计算loss用于更新生成器。这种方式使得生成器考虑到了后面k次判别器的变化情况，避免在不同mode之间切换导致的模式崩溃问题。此处务必和迭代k次生成器，然后迭代1次判别器区分开。DRAGAN则引入博弈论中的无后悔算法，改造其loss以解决mode collapse问题。前文所述的EBGAN则是加入VAE的重构误差以解决mode collapse。

方法二：针对网络结构的改进方法

​ Multi agent diverse GAN(MAD-GAN)采用多个生成器，一个判别器以保障样本生成的多样性。具体结构如下：

​ 相比于普通GAN，多了几个生成器，且在loss设计的时候，加入一个正则项。正则项使用余弦距离惩罚三个生成器生成样本的一致性。

​ MRGAN则添加了一个判别器来惩罚生成样本的mode collapse问题。具体结构如下：

​ 输入样本$x$通过一个Encoder编码为隐变量$E(x)$，然后隐变量被Generator重构，训练时，Loss有三个。$D_M$和$R$（重构误差）用于指导生成real-like的样本。而$D_D$则对$E(x)$和$z$生成的样本进行判别，显然二者生成样本都是fake samples，所以这个判别器主要用于判断生成的样本是否具有多样性，即是否出现mode collapse。

方法三：Mini-batch Discrimination

​ Mini-batch discrimination在判别器的中间层建立一个mini-batch layer用于计算基于L1距离的样本统计量，通过建立该统计量，实现了一个batch内某个样本与其他样本有多接近。这个信息可以被判别器利用到，从而甄别出哪些缺乏多样性的样本。对生成器而言，则要试图生成具有多样性的样本。

总结

下周将继续学习GAN的生成能力评价和VAE。