基于verilog的CRC校验（汇总）_verilog crc

本来想整理一下关于CRC校验的内容，但是发现前辈们写的都很好，本文对内容进行整理汇总。

原理

crc为什么能够检错和纠错，这背后有着深刻的数学原理，这里没有进行阐述，有兴趣可以阅读相关论文。这里直接拿来主义。

这篇文章似乎介绍了原理，但我没有认真看。
CRC算法原理及其Verilog实现

CRC（循环冗余校验）在线计算

CRC校验（循环冗余校验）小知识
CRC即循环冗余校验码（Cyclic Redundancy Check）：是数据通信领域中最常用的一种查错校验码，其特征是信息字段和校验字段的长度可以任意选定。循环冗余检查（CRC）是一种数据传输检错功能，对数据进行多项式计算，并将得到的结果附在帧的后面，接收设备也执行类似的算法，以保证数据传输的正确性和完整性。
CRC算法参数模型解释：
NAME：参数模型名称。
WIDTH：宽度，即CRC比特数。
POLY：生成项的简写，以16进制表示。例如：CRC-32即是0x04C11DB7，忽略了最高位的"1"，即完整的生成项是0x104C11DB7。
INIT：这是算法开始时寄存器（crc）的初始化预置值，十六进制表示。
REFIN：待测数据的每个字节是否按位反转，True或False。
REFOUT：在计算后之后，异或输出之前，整个数据是否按位反转，True或False。
XOROUT：计算结果与此参数异或后得到最终的CRC值。

常见CRC参数模型如下：

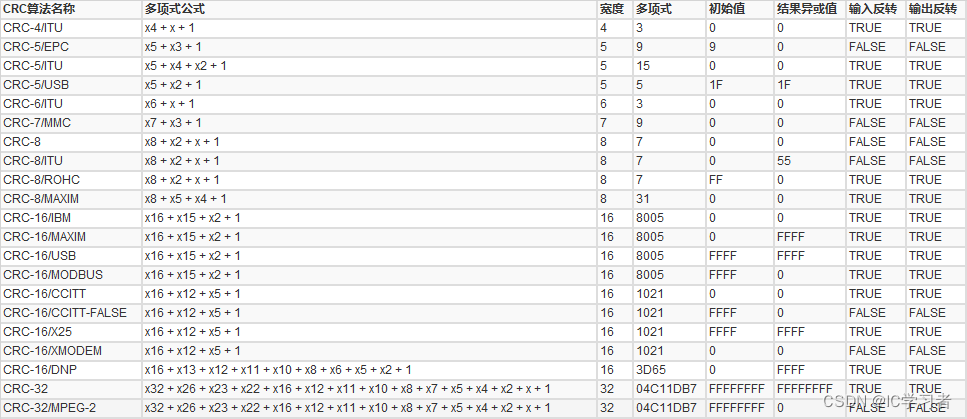
计算

下面介绍crc的计算过程，图表见原文
CRC校验原理及实现

通常如果只给了一个多项式，其他的没有说明则：INIT=0x00，REFIN=false，REFOUT=false，XOROUT=0x00。
下面手算一个CRC值，来了解CRC计算的原理。
问：原始数据：0x34，使用CRC-8/MAXIN参数模型，求CRC值？
答：根据CRC参数模型表，得到CRC-8/MAXIN的参数如下：
POLY = 0x31 = 0011 0001(最高位1已经省略)
INIT = 0x00
XOROUT = 0x00
REFIN = TRUE
REFOUT = TRUE
有了上面的参数，这样计算条件才算完整，下面来实际计算：
0.原始数据 = 0x34 = 0011 0100，多项式 = 0x31 = 1 0011 0001
1.INIT = 00，原始数据高8位和初始值进行异或运算保持不变。
2.REFIN为TRUE，需要先对原始数据进行翻转：0011 0100 > 0010 1100
3.原始数据左移8位，即后面补8个0：0010 1100 0000 0000
4.把处理之后的数据和多项式进行模2除法，求得余数：
原始数据：0010 1100 0000 0000 = 10 1100 0000 0000
多项式：1 0011 0001
模2除法取余数低8位：1111 1011
5.与XOROUT进行异或，1111 1011 xor 0000 0000 = 1111 1011
6.因为REFOUT为TRUE，对结果进行翻转得到最终的CRC-8值：1101 1111 = 0xDF
7.数据+CRC：0011 0100 1101 1111 = 34DF，相当于原始数据左移8位+余数。

上面通过笔算的方式，讲解了CRC计算的原理，下面来介绍一下如何进行校验。
按照上面CRC计算的结果，最终的数据帧：0011 0100 1101 1111 = 34DF，前8位0011 0100是原始数据，后8位1101 1111 是 CRC结果。
接收端的校验有两种方式，一种是和CRC计算一样，在本地把接收到的数据和CRC分离，然后在本地对数据进行CRC运算，得到的CRC值和接收到的CRC进行比较，如果一致，说明数据接收正确，如果不一致，说明数据有错误。
另一种方法是把整个数据帧进行CRC运算，因为是数据帧相当于把原始数据左移8位，然后加上余数，如果直接对整个数据帧进行CRC运算（除以多项式），那么余数应该为0，如果不为0说明数据出错。

注意计算的时候，异或和翻转都是以字节为单位

检错与纠错

下面介绍检错与纠错，图表见原文
循环冗余校验码原理（CRC码）

假设数据为 10101011，生成多项式为 10011，求 CRC 码？
多项式就是双方约定的除数 10011
余数 1010 就是 CRC 码的校验位，加上信息位组合成最终的 CRC 码： 101010111010
用 101010111010 与 10011 相除，最终的余数一定是 0000

一位出错(不能纠错)
若是在传输过程中，crc码被错传为101010110010
把 101010110010代入模2除，得到余数 0100，对应十进制 4，也就是说 C4 处出错了

一位出错(不能纠错)
上面的例子，校验位是 4 位，可以表示 16 种状态，实际的 CRC 码只有 12 位，所以有纠错能力。
如果校验位是 3 位，可以表示 8 种状态，实际的 CRC 码有 9 位，这种情况下就没办法实现纠错了。
假如说现在求得的余数是 010 转换为十进制是 2，能否说明第 2 位出错了呢？
看下面表，010 对应的出错位是 2 和 9，也就是说当第二位或者第九位出错了，余数是一样的，这就导致了我们根据 010 没判断出错位了。

所以要使 CRC 码有纠错能力，必须满足：2^k >= n + k + 1
n + k 表示错误的状态的数量
1 表示的正确的状态

若是多位错误，则通过上述的方法无法纠错

纠错实现

还有出错位和余数的关系是由生成多项式决定的，上述余数与出错位的关系纯属巧合，不具有普遍性。如下所示。

1100，生成多项式为1011

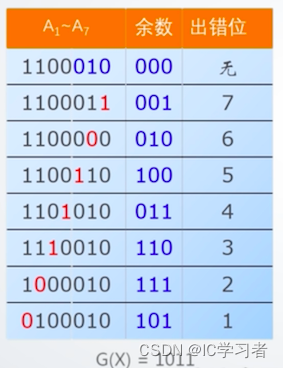
根据不同的余数的值就能知道哪一位出错了，同时理论上也能进行纠错
但是，在实际的运行中，计算机并没有对每一位都做了纠错电路，这就需要用到CRC的循环性质
假设出错位是第五位，1100010 -> 1100110，此时的余数是100，对100补个0，依然用生成多项式G去做模2运算，得到的余数是011，由表可知，恰好是第四位出错时的余数，说明余数存在循环性
利用这个性质，计算机只在第一位做纠错电路，也就是说在纠错时，计算机不知道100和011，计算机只知道第一位出错的余数是101
还是假设出错位是第五位，此时接收方拿到的是1100110，余数位100
对余数不断的进行模2运算，同时移动校验码。

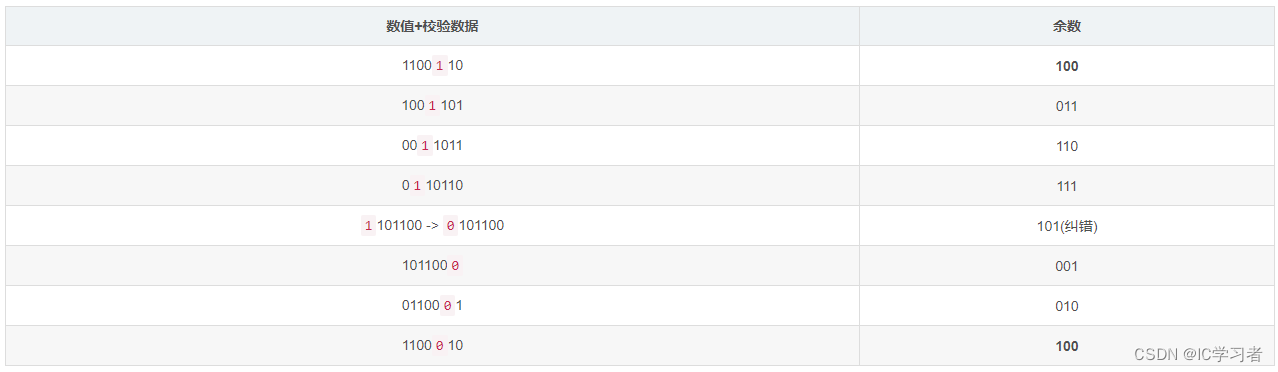
如此，就完成了第五位的纠错

Verilog实现

并入并处，需要多个时钟实现
【Verilog】CRC校验码生成器原理及verilog实现

并入并出，单时钟
CRC校验原理和verilog实现方法(三)
电路逻辑的推导见（二）

并入并出，有完整代码，单时钟
Verilog语言实现并行（循环冗余码）CRC校验

并入并出，多时钟
CRC循环冗余校验码verilog实现

多时钟强转单时钟
基于FPGA的CRC校验码生成器

This tool will generate Verilog or VHDL code for a CRC with a given data width and polynomial.
CRC Generator

FPGA手撕代码——CRC校验码的多种Verilog实现方式

FPGA/IC面试准备三之CRC校验