算法工程师-笔（面）试题汇总_算法工程师笔试题

由于精力有限，暂时先把问题和已有答案放上，后续会自己学习慢慢完善答案，还需要根据自己的理解补充更多问题和答案细节

一、算法常用概念

1.训练集(train set)、验证集(validation set)、测试集(test set)

一般需要将样本分成独立的三部分训练集(train set)，验证集(validation set)和测试集(test set)。其中训练集用来估计模型，验证集用来确定网络结构或者控制模型复杂程度的参数，而测试集则检验最终选择最优的模型的性能如何。一个典型的划分是训练集占总样本的50％，而其它各占25％，三部分都是从样本中随机抽取。

样本少的时候，上面的划分就不合适了。常用的是留少部分做测试集。然后对其余N个样本采用K折交叉验证法。就是将样本打乱，然后均匀分成K份，轮流选择其中K－1份训练，剩余的一份做验证，计算预测误差平方和，最后把K次的预测误差平方和再做平均作为选择最优模型结构的依据。特别的K取N，就是留一法（leave one out）。

training set是用来训练模型或确定模型参数的，如ANN中权值等；

validation set是用来做模型选择（model selection），即做模型的最终优化及确定的，如ANN的结构；

test set则纯粹是为了测试已经训练好的模型的推广能力。当然，test set这并不能保证模型的正确性，他只是说相似的数据用此模型会得出相似的结果。但实际应用中，一般只将数据集分成两类，即training set 和test set，大多数文章并不涉及validation set。

2.交叉验证（Cross-validation）

将训练集分成k份，每次取（k-1）份用于训练model，1份用于验证（或言之：测试），再通过某种metric进行打分；然后再选择不同的（k-1）份重新训练model，1份用于对该model进行验证，再通过某种metric进行打分....。最终，我们得到了k个分数，取平均，我们就可以知道这个model的分数了，多用于对模型参数（即超参数。普通参数model会自己习得，比如线性模型中的θ每个特征的权重）的选择。此时，选用不同超参的模型,可看作“不同的estimator”，然后我们用交叉验证对这个estimator打平均分，从而通过这个平均分对estimator的超参数进行选择。

3.什么是Bias(偏差)、 Variance(方差)、Noise(噪声)

Bias反映的是模型在样本上的输出与真实值之间的误差，即模型预测值与真实值的差异，也即算法本身的拟合能力，是由使用的学习算法的某些错误或过于简单的假设造成的误差。它会导致模型欠拟合，很难有高的预测准确率。

Variance反映的是模型每一次输出结果与模型输出期望之间的误差，即不同训练数据训练的模型的预测值之间的差异，也即模型的稳定性，反应预测的波动情况，是由于使用的算法模型过于复杂，导致对训练数据的变化十分敏感，这样会导致模型过拟合，使得模型带入了过多的噪音。

Noise就不是你想要的真正数据，你可以想象为来破坏你实验的元凶和造成你可能过拟合的原因之一，至于为什么是过拟合的原因，因为模型过度追求Low Bias会导致训练过度，对测试集判断表现优秀，导致噪声点也被拟合进去了

4.高偏差和高方差说明了什么？

1）数据欠拟合会出现高偏差问题。

2）数据过度拟合会出现高方差问题。

3）怎么处理高偏差和高方差问题：

 高偏差：训练误差很大，训练误差与测试误差差距小，随着样本数据增多，训练误差增大。

 解决方法：寻找更具代表性的特征、.用更多的特征（增大输入向量的维度）

 高方差：训练误差小，训练误差与测试误差差距大，可以通过增大样本集合来减小差距。随着样本数据增多，测试误差会减小。

 解决方案：增大数据集合（使用更多的数据）、减少数据特征（减小数据维度）

 一般采取判断某函数是高方差还是高偏差，简单的判断是看训练误差与测试误差的差距，差距大说明是高方差的，差距小说明是高偏差的。

5.什么是监督学习和无监督学习

监督学习需要具有标签（label）的训练数据，比如做分类，你需要先对训练数据做标记，然后才能训练模型将数据分成你说需要的标记类。

而非监督学习则不需要。

6.过拟合怎么解决，L1和L2正则化有什么区别

剪枝处理：是决策树学习算法对付“过拟合”的主要手段。可以分为自上而下和自下而上两种。常见的方法有：误差降低剪枝（REP）和代价复杂度剪枝（CCP）。REP简单的来说就是对树的每一个结点进行剪枝，如果剪掉某个结点不会降低模型准确率，那么将其剪掉。这种启发式的做法实际上就是为了最大化准确率。

卷积神经网络中，使用dropout策略来缓解过拟合。

BP算法表示能力强，但易过拟合，两种常用来缓解过拟合的策略：“早停”和“正则化”。

“早停”：将数据分为训练集和验证集，训练集用来计算梯度、更新连接权和阈值，验证集用来估计误差，若训练集误差降低但验证集误差升高，则停止训练，同时返回具有最小验证集误差的连接权和阈值。

“正则化”：基本思想是在误差目标函数中增加一个用于描述网络复杂度的部分，例如连接权与阈值的平方和。

对于线性回归模型，使用L1正则化的模型建叫做Lasso回归，使用L2正则化的模型叫做Ridge回归（岭回归）。

L1正则化是指权值向量w中各个元素的绝对值之和，通常表示为||w||1，相当于加入了一个laplacean prior，也有个美称叫“稀疏规则算子”（Lasso regularization）。L1正则化可以产生稀疏权值矩阵，即产生一个稀疏模型，可以用于特征选择。

L2正则化是指权值向量w中各个元素的平方和然后再求平方根（可以看到Ridge回归的L2正则化项有平方符号），通常表示为||w||2，保留显著减小损失函数方向上的权重，而对于那些对函数值影响不大的权重使其衰减接近于0，相当于加入一个gaussian prio。又称Euclidean范数或Frobenius范数。L2正则化可以防止模型过拟合（overfitting），，提升模型的泛化能力。一定程度上，L1也可以防止过拟合。

Lp正则化: 为x向量各个元素绝对值p次方和的1/p次方.

7.第一类误差和第二类误差有什么区别？

第一类误差指的是假正率，第二类指的是假负率。简单来说，第一类误差意味着假设为真的情况下，作出了拒绝原假设的一种错误推断。第二类误差意味着假设为假的情况下，做出了接受原假设的一种错误判断。

举个例子：第一类误差，你告诉一个男的他怀孕了。第二类误差，你告诉一个已经怀孕的女子，她没怀孕。

8.什么是傅立叶变换？

傅立叶变换指：一个满足某些条件的函数可以表示成三角函数或他们的积分形式的线性组合。

二、机器学习算法

9.生成模型与判别模型有什么区别？

生成模型会学习数据的分布；判别模型学习的是不同类型数据之间的区别，不学习数据内部特点。在分类问题上，判别模型会优于生成模型。

判别模型求解的思路是：条件分布------>模型参数后验概率最大------->（似然函数、参数先验）最大------->最大似然

生成模型的求解思路是：联合分布------->求解类别先验概率和类别条件概率

常见的生成方法有混合高斯模型、朴素贝叶斯法和隐形马尔科夫模型等，常见的判别方法有SVM、LR等

10.给出KNN(即最近邻算法)的模型、原理

k-Nearest Neighbors 是一种监督学习算法，而k-means是非监督的。这两种算法看起来很相似，都需要计算样本之间的距离。KNN需要事先已有标注好的数据，当你需要对未标注的数据进行分类时，统计它附近最近的k个样本，将其划分为样本数最多的类别中。k-means聚类只需要一些未分类的数据点和阀值，算法会逐渐将样本点进行分成族类。KNN主要过程为：

　　

　　如何选择一个最佳的K值，这取决于数据。一般情况下，在分类时较大的K值能够减小噪声的影响。但会使类别之间的界限变得模糊。一个较好的K值可通过各种启发式技术来获取，比如，交叉验证。另外噪声和非相关性特征向量的存在会使K近邻算法的准确性减小。

　　近邻算法具有较强的一致性结果。随着数据趋于无限，算法保证错误率不会超过贝叶斯算法错误率的两倍。对于一些好的K值，K近邻保证错误率不会超过贝叶斯理论误差率。

注：马氏距离一定要先给出样本集的统计性质，比如均值向量，协方差矩阵等。关于马氏距离的介绍如下：

优点：

　　1. 思想简单，理论成熟，既可以用来做分类也可以用来做回归；

　　2. 可用于非线性分类；

　　3. 训练时间复杂度为O(n)；

　　4. 准确度高，对数据没有假设，对outlier不敏感；

缺点：

　　1. 需要设定K值，

2. 计算量大，需要计算样本集中每个样本的距离；

　　3. 样本不平衡问题（即有些类别的样本数量很多，而其它样本的数量很少）；

　　4. 需要大量的内存；

11.朴素贝叶斯

之所以称“朴素”，是因为我们在用到它的时候，有一个很强的假设（现实数据中几乎不会出现的）：我们假设特征之间是相互独立，也就是我们计算条件概率时可以简化成它的组件的条件概率乘积。

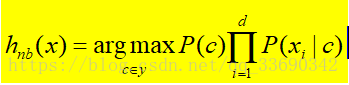
1. 如果给出的特征向量长度可能不同，这是需要归一化为通长度的向量（这里以文本分类为例），比如说是句子单词的话，则长度为整个词汇量的长度，对应位置是该单词出现的次数。　　2. 计算公式如下：

 　　

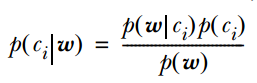
　　其中一项条件概率可以通过朴素贝叶斯条件独立展开。要注意一点就是 的计算方法，而由朴素贝叶斯的前提假设可知，

 =  ，因此一般有两种，一种是在类别为ci的那些样本集中，找到wj出现次数的总和，然后除以该样本的总和；第二种方法是类别为ci的那些样本集中，找到wj出现次数的总和，然后除以该样本中所有特征出现次数的总和。

　　3. 如果 中的某一项为0，则其联合概率的乘积也可能为0，即2中公式的分子为0，为了避免这种现象出现，一般情况下会将这一项初始化为1，当然为了保证概率相等，分母应对应初始化为2（这里因为是2类，所以加2，如果是k类就需要加k，术语上叫做laplace光滑, 分母加k的原因是使之满足全概率公式）。

优点：对小规模的数据表现很好；适合多分类任务；适合增量式训练。

缺点：对输入数据的表达形式很敏感。

12.决策树的ID3，C4.5，CART等，决策树的split原理和剪枝策略

决策树中很重要的一点就是选择一个属性进行分枝，因此要注意一下信息增益的计算公式，并深入理解它。

　　信息熵的计算公式如下:

 　　

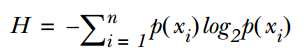
　　其中的n代表有n个分类类别（比如假设是2类问题，那么n=2）。分别计算这2类样本在总样本中出现的概率p1和p2，这样就可以计算出未选中属性分枝前的信息熵。

　　现在选中一个属性xi用来进行分枝，此时分枝规则是：如果xi=vx的话，将样本分到树的一个分支；如果不相等则进入另一个分支。很显然，分支中的样本很有可能包括2个类别，分别计算这2个分支的熵H1和H2,计算出分枝后的总信息熵H’=p1*H1+p2*H2.，则此时的信息增益ΔH=H-H’。以信息增益为原则，把所有的属性都测试一边，选择一个使增益最大的属性作为本次分枝属性。

　　决策树的优点：计算量简单，可解释性强，比较适合处理有缺失属性值的样本，能够处理不相关的特征；

　　缺点：容易过拟合（后续出现了随机森林，减小了过拟合现象）；

13.给出逻辑回归的模型、原理

LR算法实现参考地址：https://blog.csdn.net/Trisyp/article/details/89318333

假设限制有一些数据点，我们利用一条直线对这些点进行拟合（该线称为最佳拟合直线），这个拟合过程就称为回归。logistic回归进行分类的思想是：根据现有数据对分类边界线建立回归公式，以此进行分类。训练分类器时的做法就是寻找最佳拟合参数，使用的是最优化算法。

z=w0x0+w1x1+w2x2+⋯ +wnxn

Logistic回归分类器，我们在每一个特征上都乘以一个回归系数，然后把所有的结果值相加，将这个总和代入Sigmoid函数中，进而得到一个范围在0~1之间的数值。任何大于0.5的数据都被分入1类，小于0.5的即被归入0类。所以，logistic回归也可以被看成是一种概率估计。

Logistic是一种线性分类器，需要注意的地方有：

1. logistic函数表达式为：

 　　

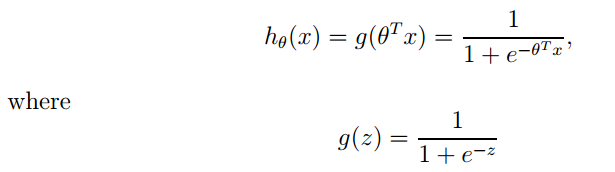
　　其导数形式为：

 　　

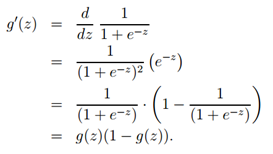
　　2. logistic回归方法主要是用最大似然估计来学习的，所以单个样本的后验概率为：

 　　

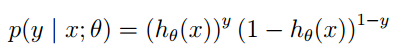
　　到整个样本的后验概率：

 　　

　　其中：

 　　

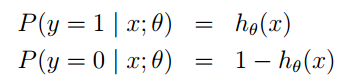
　　通过对数进一步化简为：

 　　

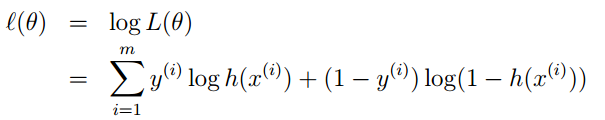
　　3. 其实它的loss function为-l(θ)，因此我们需使loss function最小，可采用梯度下降法得到。梯度下降法公式为:

 　　

　　

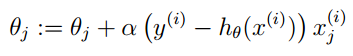
　　优点：

　　1、实现简单；

　　2、分类时计算量非常小，速度很快，存储资源低；

　　缺点：

　　1、容易欠拟合，一般准确度不太高

2、只能处理两分类问题（在此基础上衍生出来的softmax可以用于多分类），且必须线性可分；

14.随机梯度下降算法的原理和具体迭代函数

随机梯度上升算法的伪代码：

所有回归系数初始化为1;

对数据集中的每个样本:

              计算该样本的梯度;

              使用更新回归系数;

返回回归系数值;

15.Bagging 和 Boosting的区别

首先来看看Adaboost的流程图，如下：

 　　

　　从图中可以看到，在训练过程中我们需要训练出多个弱分类器（图中为3个），每个弱分类器是由不同权重的样本（图中为5个训练样本）训练得到（其中第一个弱分类器对应输入样本的权值是一样的），而每个弱分类器对最终分类结果的作用也不同，是通过加权平均输出的，权值见上图中三角形里面的数值。那么这些弱分类器和其对应的权值是怎样训练出来的呢？

　　下面通过一个例子来简单说明。

　　书中（machine learning in action）假设的是5个训练样本，每个训练样本的维度为2，在训练第一个分类器时5个样本的权重各为0.2. 注意这里样本的权值和最终训练的弱分类器组对应的权值α是不同的，样本的权重只在训练过程中用到，而α在训练过程和测试过程都有用到。

　　现在假设弱分类器是带一个节点的简单决策树，该决策树会选择2个属性（假设只有2个属性）的一个，然后计算出这个属性中的最佳值用来分类。

　　Adaboost的简单版本训练过程如下：

　　1. 训练第一个分类器，样本的权值D为相同的均值。通过一个弱分类器，得到这5个样本（请对应书中的例子来看，依旧是machine learning in action）的分类预测标签。与给出的样本真实标签对比，就可能出现误差(即错误)。如果某个样本预测错误，则它对应的错误值为该样本的权重，如果分类正确，则错误值为0. 最后累加5个样本的错误率之和，记为ε。

　　2. 通过ε来计算该弱分类器的权重α，公式如下：

 　　

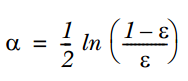
　　3. 通过α来计算训练下一个弱分类器样本的权重D，如果对应样本分类正确，则减小该样本的权重，公式为：

 　　

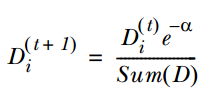
　　如果样本分类错误，则增加该样本的权重，公式为：

 　　

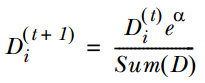
　　4. 循环步骤1,2,3来继续训练多个分类器，只是其D值不同而已。

　　测试过程如下：

　　输入一个样本到训练好的每个弱分类中，则每个弱分类都对应一个输出标签，然后该标签乘以对应的α，最后求和得到值的符号即为预测标签值。

　　Boosting算法的优点：低泛化误差；容易实现，分类准确率较高，没有太多参数可以调；

　　缺点：对outlier比较敏感；

16.GBDT模型的损失函数、建模原理，以及如何调参？

待回答。

17.GBDT和XGBoost的区别是什么？

XGBoost类似于GBDT的优化版，不论是精度还是效率上都有了提升。与GBDT相比，具体的优点有：

1.损失函数是用泰勒展式二项逼近，而不是像GBDT里的就是一阶导数；

2.对树的结构进行了正则化约束，防止模型过度复杂，降低了过拟合的可能性；

3.节点分裂的方式不同，GBDT是用的基尼系数，XGBoost是经过优化推导后的。

18.随机森林和GBDT的区别：

随机森林采用的bagging思想，而GBDT采用的boosting思想。这两种方法都是Bootstrap思想的应用，Bootstrap是一种有放回的抽样方法思想。虽然都是有放回的抽样，但二者的区别在于：Bagging采用有放回的均匀取样，而Boosting根据错误率来取样（Boosting初始化时对每一个训练样例赋相等的权重1／n，然后用该算法对训练集训练t轮，每次训练后，对训练失败的样例赋以较大的权重），因此Boosting的分类精度要优于Bagging。Bagging的训练集的选择是随机的，各训练集之间相互独立，弱分类器可并行，而Boosting的训练集的选择与前一轮的学习结果有关，是串行的。

组成随机森林的树可以是分类树，也可以是回归树；而GBDT只能由回归树组成。

组成随机森林的树可以并行生成；而GBDT只能是串行生成。

对于最终的输出结果而言，随机森林采用多数投票等；而GBDT则是将所有结果累加起来，或者加权累加起来。

随机森林对异常值不敏感；GBDT对异常值非常敏感。

随机森林对训练集一视同仁；GBDT是基于权值的弱分类器的集成。

随机森林是通过减少模型方差提高性能；GBDT是通过减少模型偏差提高性能

19.GB和牛顿法的区别，它们和泰勒公式的关系

待回答

20.为什么用最小二乘而不是最小四乘

待回答

21.怎么理解损失函数，SVM的损失函数是什么，写出公式

损失函数是用来测度模型输出值和真实的因变量值之间差异的函数，模型输出值p和和真实值y之间的差异一般称为残差或者误差，但是这个值并不能直接用来衡量模型的质量，当一个模型完美的时候，其误差为0，而当一个模型不够完美时，其误差不论是负值还是正值，都偏离0，因此衡量模型质量的误差偏离0的相对值，即误差函数的值越接近于0，模型的性能越好，反之模型的性能越差。常用的损失函数如下：

均方差（MSE）误差函数：  ，这种损失函数常用在实数值域连续变量的回归问题上，并且对于残差较大的情况给与更多的权重。

平均绝对差(MAE)：，这种损失函数也常用在实数值域连续变量的回归问题上，在时间序列预测问题中也常用。在这个误差函数中每个误差点对总体误差的贡献与其误差绝对值成线性比例关系，而上面的MSE没有此特性。

交叉熵损失函数(Cross-Entropy):这种损失函数也叫对数损失函数，是针对分类模型的性能比较设计的，按照分类模型是二分类还是多分类的区别，可以分为二分类交叉熵和多分类交叉熵两种,交叉熵的数学表达式如下：

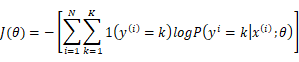
因此交叉熵可以解释为映射到最可能类别的概率的对数。因此，当预测值的分布和实际因变量的分布尽可能一致时，交叉熵最小。

SVM的损失函数：常用的是径向基函数（RBF）:

22.SVM的原理及公式推导：

SVM算法实现参考地址：https://blog.csdn.net/Trisyp/article/details/89350825

1. svm中的最优分类面是对所有样本的几何裕量最大（为什么要选择最大间隔分类器，请从数学角度上说明？网易深度学习岗位面试过程中有被问到。答案就是几何间隔与样本的误分次数间存在关系： ，其中的分母就是样本到分类间隔距离，分子中的R是所有样本中的最长向量值），即：

 　　

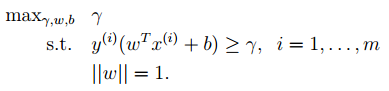
　　经过一系列推导可得为优化下面原始目标：

　　
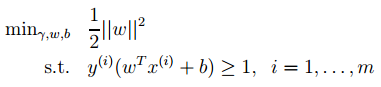
　　2. 下面来看看拉格朗日理论：

　　
　　可以将1中的优化目标转换为拉格朗日的形式（通过各种对偶优化，KKD条件），最后目标函数为：

 　　

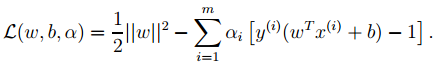
　　我们只需要最小化上述目标函数，其中的α为原始优化问题中的不等式约束拉格朗日系数。

　　3. 对2中最后的式子分别w和b求导可得：

　　

　　 

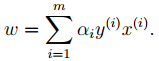
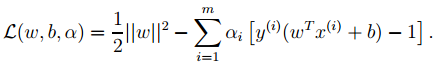
　　由上面第1式子可以知道，如果我们优化出了α，则直接可以求出w了，即模型的参数搞定。而上面第2个式子可以作为后续优化的一个约束条件。

　　4. 对2中最后一个目标函数用对偶优化理论可以转换为优化下面的目标函数：

　　
　　而这个函数可以用常用的优化方法求得α，进而求得w和b。

　　5. 按照道理，svm简单理论应该到此结束。不过还是要补充一点，即在预测时有：

 　　

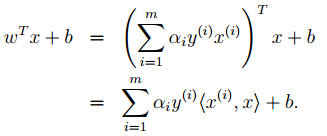
　　那个尖括号我们可以用核函数代替，这也是svm经常和核函数扯在一起的原因。

　　6. 最后是关于松弛变量的引入，因此原始的目标优化公式为：

 　　

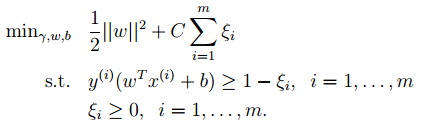
　　此时对应的对偶优化公式为：

 　　

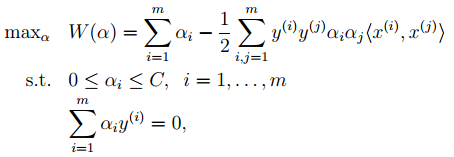
　　与前面的相比只是α多了个上界。

　　优点：可用于线性/非线性分类，也可以用于回归；

　　低泛化误差；容易解释；计算复杂度较低；

　　缺点：

　　对参数和核函数的选择比较敏感；

　　原始的SVM只比较擅长处理二分类问题；

23.LogisticRegression和SVM的联系与区别？

联系：

1、LR和SVM都可以处理分类问题，且一般都用于处理线性二分类问题（在改进的情况下可以处理多分类问题）

2、两个方法都可以增加不同的正则化项，如L1、L2等等。所以在很多实验中，两种算法的结果是很接近的。

区别：

1、LR是参数模型，SVM是非参数模型。

2、从目标函数来看，区别在于逻辑回归采用的是Logistical Loss，SVM采用的是hinge loss.这两个损失函数的目的都是增加对分类影响较大的数据点的权重，减少与分类关系较小的数据点的权重。

3、SVM的处理方法是只考虑Support Vectors，也就是和分类最相关的少数点，去学习分类器。而逻辑回归通过非线性映射，大大减小了离分类平面较远的点的权重，相对提升了与分类最相关的数据点的权重。

4、逻辑回归相对来说模型更简单，好理解，特别是大规模线性分类时比较方便。而SVM的理解和优化相对来说复杂一些，SVM转化为对偶问题后,分类只需要计算与少数几个支持向量的距离,这个在进行复杂核函数计算时优势很明显,能够大大简化模型和计算。

5、Logic 能做的 SVM能做，但可能在准确率上有问题，SVM能做的Logic有的做不了。

24.聚类过程

根据聚类思想划分：

　　1. 基于划分的聚类:

K-Means算法实现参考地址：https://blog.csdn.net/Trisyp/article/details/89499998　　

K-means, k-medoids(每一个类别中找一个样本点来代表),CLARANS.

　　k-means是使下面的表达式值最小：

 　　

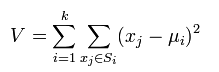
　　 k-means算法的优点：

　　（1）k-means算法是解决聚类问题的一种经典算法，算法简单、快速。

　　（2）对处理大数据集，该算法是相对可伸缩的和高效率的，因为它的复杂度大约是O(nkt)，其中n是所有对象的数目，k是簇的数目,t是迭代的次数。通常k<<n。这个算法通常局部收敛。

　　（3）算法尝试找出使平方误差函数值最小的k个划分。当簇是密集的、球状或团状的，且簇与簇之间区别明显时，聚类效果较好。

　　 缺点：

　　（1）k-平均方法只有在簇的平均值被定义的情况下才能使用，且对有些分类属性的数据不适合。

　　（2）要求用户必须事先给出要生成的簇的数目k。

　　（3）对初值敏感，对于不同的初始值，可能会导致不同的聚类结果。

　　（4）不适合于发现非凸面形状的簇，或者大小差别很大的簇。

　　（5）对于"噪声"和孤立点数据敏感，少量的该类数据能够对平均值产生极大影响。

　　2. 基于层次的聚类：

　　自底向上的凝聚方法，比如AGNES。

　　自上向下的分裂方法，比如DIANA。

　　3. 基于密度的聚类：

　　DBSACN,OPTICS,BIRCH(CF-Tree),CURE.

　　4. 基于网格的方法：

　　STING, WaveCluster.

　　5. 基于模型的聚类：

　　EM,SOM,COBWEB.

25.神经网络如何工作

激活函数：大多数神经元都将一维向量的网络输入变量通过一个函数映射到另外一个一维向量的数值，这个函数被称为激活函数。

如果输入变化很小，导致输出结构发生截然不同的结果，这种情况是我们不希望看到的，为了模拟更细微的变化，输入和输出数值不只是0到1，可以是0和1之间的任何数，激活函数是用来加入非线性因素的，因为线性模型的表达力不够 。

这句话字面的意思很容易理解，但是在具体处理图像的时候是什么情况呢？我们知道在神经网络中，对于图像，我们主要采用了卷积的方式来处理，也就是对每个像素点赋予一个权值，这个操作显然就是线性的。但是对于我们样本来说，不一定是线性可分的，为了解决这个问题，我们可以进行线性变化，或者我们引入非线性因素，解决线性模型所不能解决的问题。

这里插一句，来比较一下上面的那些激活函数，因为神经网络的数学基础是处处可微的，所以选取的激活函数要能保证数据输入与输出也是可微的，运算特征是不断进行循环计算，所以在每代循环过程中，每个神经元的值也是在不断变化的。

这就导致了tanh特征相差明显时的效果会很好，在循环过程中会不断扩大特征效果显示出来，但有是，在特征相差比较复杂或是相差不是特别大时，需要更细微的分类判断的时候，sigmoid效果就好了。

还有一个东西要注意，sigmoid 和 tanh作为激活函数的话，一定要注意一定要对 input 进行归一化，否则激活后的值都会进入平坦区，使隐层的输出全部趋同，但是 ReLU 并不需要输入归一化来防止它们达到饱和。

构建稀疏矩阵，也就是稀疏性，这个特性可以去除数据中的冗余，最大可能保留数据的特征，也就是大多数为0的稀疏矩阵来表示。其实这个特性主要是对于Relu，它就是取的max(0,x)，因为神经网络是不断反复计算，实际上变成了它在尝试不断试探如何用一个大多数为0的矩阵来尝试表达数据特征，结果因为稀疏特性的存在，反而这种方法变得运算得又快效果又好了。所以我们可以看到目前大部分的卷积神经网络中，基本上都是采用了ReLU 函数。

26.常用的激活函数

激活函数应该具有的性质：

（1）非线性。线性激活层对于深层神经网络没有作用，因为其作用以后仍然是输入的各种线性变换。。

（2）连续可微。梯度下降法的要求。

（3）范围最好不饱和，当有饱和的区间段时，若系统优化进入到该段，梯度近似为0，网络的学习就会停止。

（4）单调性，当激活函数是单调时，单层神经网络的误差函数是凸的，好优化。

（5）在原点处近似线性，这样当权值初始化为接近0的随机值时，网络可以学习的较快，不用可以调节网络的初始值。

目前常用的激活函数都只拥有上述性质的部分，没有一个拥有全部的～～

Sigmoid函数 ：

目前已被淘汰

缺点：

① 饱和时梯度值非常小。由于BP算法反向传播的时候后层的梯度是以乘性方式传递到前层，因此当层数比较多的时候，传到前层的梯度就会非常小，网络权值得不到有效的更新，即梯度耗散。如果该层的权值初始化使得f(x) 处于饱和状态时，网络基本上权值无法更新。

② 输出值不是以0为中心值。

Tanh双曲正切函数：

其中σ(x) 为sigmoid函数，仍然具有饱和的问题。

ReLU函数：

Alex在2012年提出的一种新的激活函数。该函数的提出很大程度的解决了BP算法在优化深层神经网络时的梯度耗散问题

优点：

•  x>0 时，梯度恒为1，无梯度耗散问题，收敛快；

② 增大了网络的稀疏性。当x<0 时，该层的输出为0，训练完成后为0的神经元越多，稀疏性越大，提取出来的特征就约具有代表性，泛化能力越强。即得到同样的效果，真正起作用的神经元越少，网络的泛化性能越好

③ 运算量很小；

缺点：

如果后层的某一个梯度特别大，导致W更新以后变得特别大，导致该层的输入<0，输出为0，这时该层就会‘die’，没有更新。当学习率比较大时可能会有40%的神经元都会在训练开始就‘die’，因此需要对学习率进行一个好的设置。

由优缺点可知max(0,x) 函数为一个双刃剑，既可以形成网络的稀疏性，也可能造成有很多永远处于‘die’的神经元，需要tradeoff。

Leaky ReLU函数：

改善了ReLU的死亡特性，但是也同时损失了一部分稀疏性，且增加了一个超参数，目前来说其好处不太明确

Maxout函数：

泛化了ReLU和Leaky ReLU，改善了死亡特性，但是同样损失了部分稀疏性，每个非线性函数增加了两倍的参数

真实使用的时候最常用的还是ReLU函数，注意学习率的设置以及死亡节点所占的比例即可

注意：

1）对于输出层，应当尽量选择适合因变量分布的激活函数：

2）对于只有0，1取值的双值因变量，logistic函数是一个比较好的选择。

3）对于有多个取值的离散因变量，比如0到9数字识别，softmax激活函数是logistic激活函数的自然衍生。

4）对于有限值域的连续因变量logistic或者tanh激活函数都可以用，但是需要将因变量的值域伸缩到logistic或tanh对应的值域中。

5）如果因变量取值为正，但是没有上限，那么指数函数是一个较好的选择。

6）如果因变量没有有限值域，或者虽然有限值域但是边界未知，那么最好采用线性函数作为激活函数。

27.EM算法

有时候因为样本的产生和隐含变量有关（隐含变量是不能观察的），而求模型的参数时一般采用最大似然估计，由于含有了隐含变量，所以对似然函数参数求导是求不出来的，这时可以采用EM算法来求模型的参数的（对应模型参数个数可能有多个），EM算法一般分为2步：

　　E步：选取一组参数，求出在该参数下隐含变量的条件概率值；

　　M步：结合E步求出的隐含变量条件概率，求出似然函数下界函数（本质上是某个期望函数）的最大值。

　　重复上面2步直至收敛。

　　公式如下所示：

 　　

　　M步公式中下界函数的推导过程：

 　　

　　EM算法一个常见的例子就是GMM模型，每个样本都有可能由k个高斯产生，只不过由每个高斯产生的概率不同而已，因此每个样本都有对应的高斯分布（k个中的某一个），此时的隐含变量就是每个样本对应的某个高斯分布。

　　GMM的E步公式如下（计算每个样本对应每个高斯的概率）：

 　　

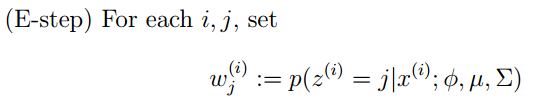
　　更具体的计算公式为：

　　

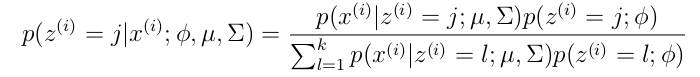
　　M步公式如下（计算每个高斯的比重，均值，方差这3个参数）：

 　　

28.Apriori算法

Apriori是关联分析中比较早的一种方法，主要用来挖掘那些频繁项集合。其思想是：

　　1. 如果一个项目集合不是频繁集合，那么任何包含它的项目集合也一定不是频繁集合；

　　2. 如果一个项目集合是频繁集合，那么它的任何非空子集也是频繁集合；

　　Aprioir需要扫描项目表多遍，从一个项目开始扫描，舍去掉那些不是频繁的项目，得到的集合称为L，然后对L中的每个元素进行自组合，生成比上次扫描多一个项目的集合，该集合称为C，接着又扫描去掉那些非频繁的项目，重复…

　　看下面这个例子：

　　元素项目表格：

 　　

　　如果每个步骤不去掉非频繁项目集，则其扫描过程的树形结构如下：

 　　

　　在其中某个过程中，可能出现非频繁的项目集，将其去掉（用阴影表示）为：

 　　

29.FP Growth算法

　　FP Growth是一种比Apriori更高效的频繁项挖掘方法，它只需要扫描项目表2次。其中第1次扫描获得当个项目的频率，去掉不符合支持度要求的项，并对剩下的项排序。第2遍扫描是建立一颗FP-Tree(frequent-patten tree)。

　　接下来的工作就是在FP-Tree上进行挖掘。

　　比如说有下表：

 　　

　　它所对应的FP_Tree如下：

 　　

　　然后从频率最小的单项P开始，找出P的条件模式基，用构造FP_Tree同样的方法来构造P的条件模式基的FP_Tree，在这棵树上找出包含P的频繁项集。

　　依次从m,b,a,c,f的条件模式基上挖掘频繁项集，有些项需要递归的去挖掘，比较麻烦，比如m节点

30.什么是核技巧，有什么用处？

核技巧使用核函数，确保在高维空间不需要明确计算点的坐标，而是计算数据的特征空间中的内积。这使其具有一个很有用的属性：更容易的计算高维空间中点的坐标。许多算法都可以表示称这样的内积形式，使用核技巧可以保证低维数据在高维空间中运用算法进行计算。

参考网址：

机器学习&数据挖掘笔记_16（常见面试之机器学习算法思想简单梳理） - tornadomeet - 博客园

41个机器学习面试题_喂鱼W_y的博客-CSDN博客