蓝桥杯——2020第十一届C/C++真题[省赛][B组]_十一届蓝桥杯字串排序

目录

门牌制作

既约分数

蛇形填数

七段码

跑步锻炼

 回文日期

字串排序​

成绩统计

子串分值和

平面切分

---

门牌制作

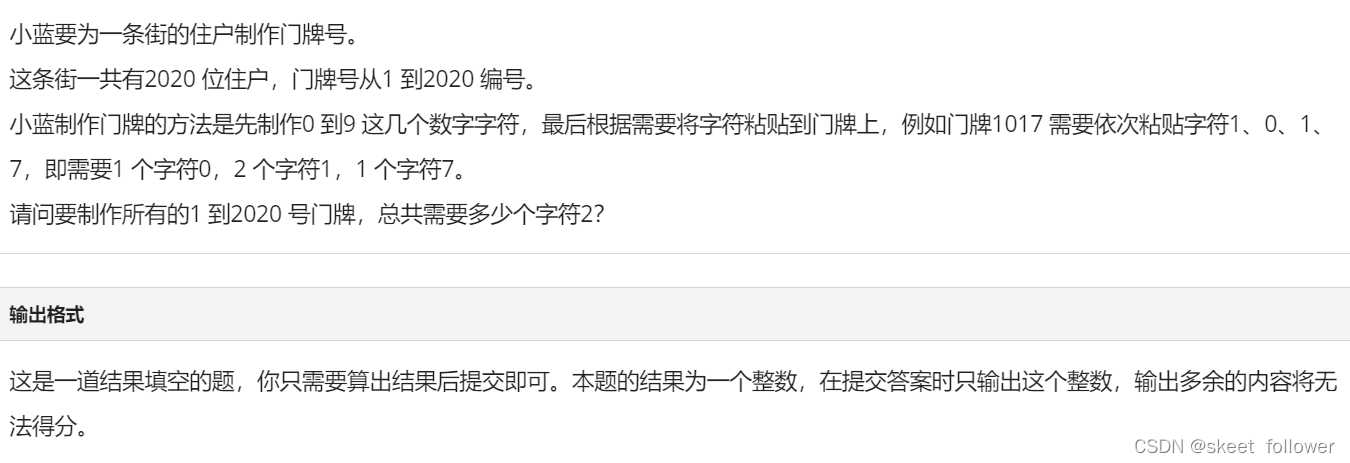
思路:很简单,枚举每个数的每一位,看是否等于2，等于则++；

代码

#include<iostream>
using namespace std;
int co;
void check(int k)
{
	while (k > 0)
	{
		int m = k % 10;
		k /= 10;
		if (m == 2)
		{
			co++;
		}
	}
}
int main()
{
	for (int i = 1; i <= 2020; i++)
	{
		check(i);
	}
	cout << co << endl;
	return 0;
}

答案:624 

既约分数

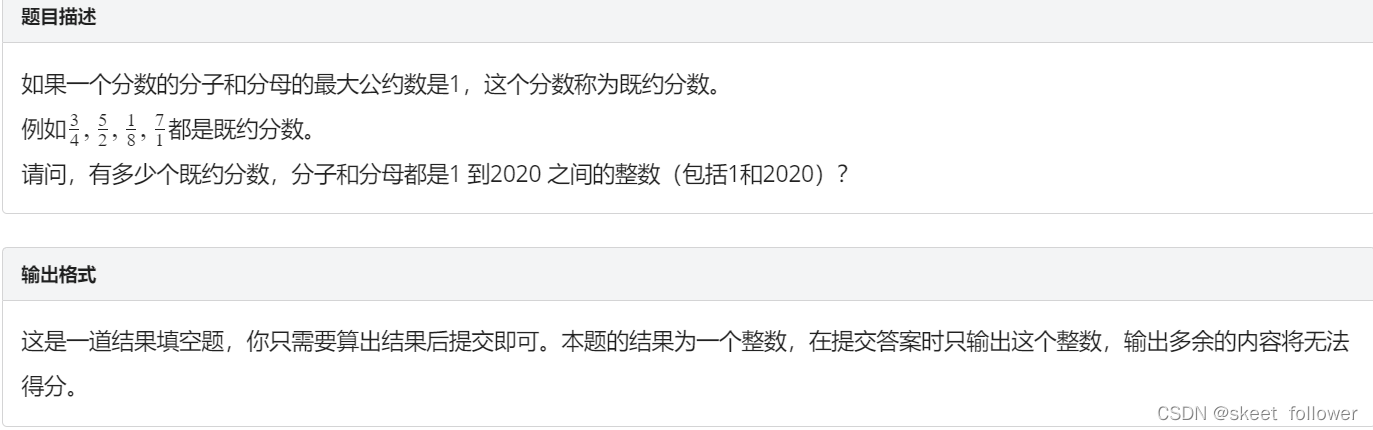
思路: 这题就是考最大公约数,不过要细心,求出来最大公约数后,要*2,因为分子和分母可以互换,又是不同的情况,还有1/1,2/2,3/3....这样的要算为一种情况,所以求出来结果还要+1.

代码

#include<iostream>
using namespace std;
int ants;
int gcd(int a, int b)
{
	/*return b ? gcd(b, a % b) : a;*/
	if (a%b == 0)return b;
	return gcd(b, a % b);
}
int main()
{
	for (int i = 1; i <= 2020; i++)
	{
		for (int j = i+1; j <= 2020; j++)
		{
			if (gcd(i, j) == 1)
			{
				ants++;
			}
			
		}
	}
	int sum = ants * 2 + 1;
	cout <<sum << endl;
	return 0;
}

 答案:2481215

蛇形填数

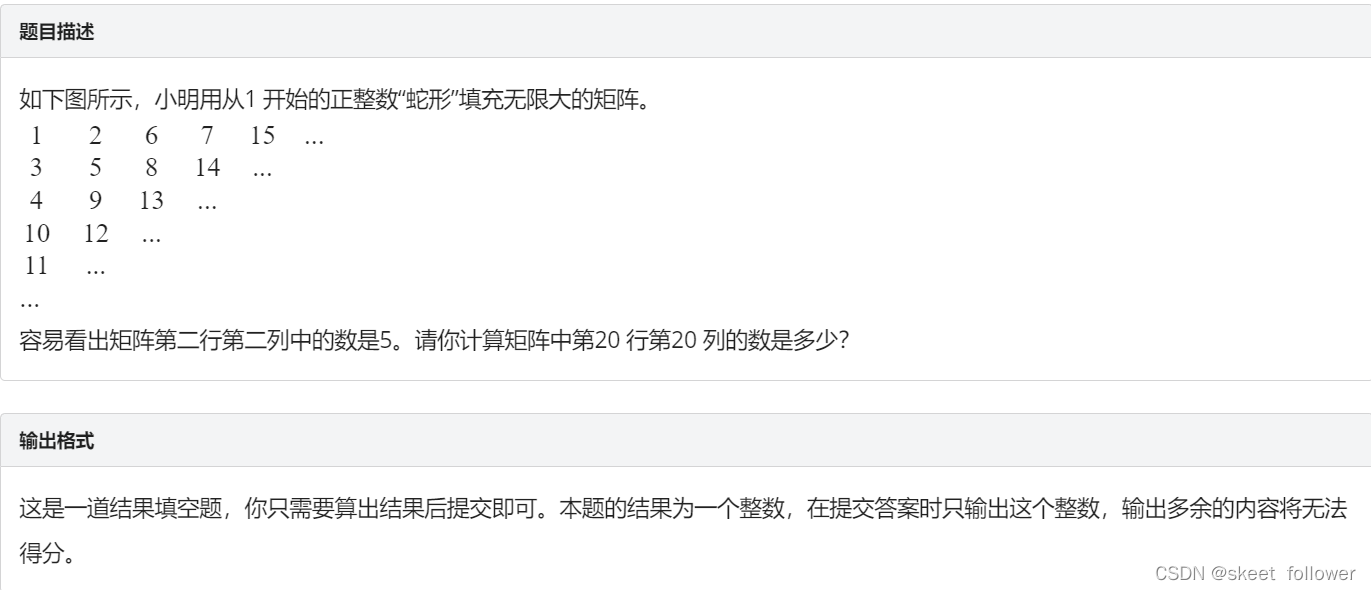
 思路:这样的题就是找规律,对代码要求不高,多写几个就找出来了

代码:

#include<iostream>
using namespace std;
int main()
{
	int n = 20, sum = 1;
	for (int i = 0; i <n; i++)
	{
		sum += i * 4;
	}
	cout << sum << endl;
	return 0;
}

答案:761 

七段码

思路: DFS搜索所有状态，判断每种状态可不可行。判断的方法是把每条灯管当作一个节点，编号，连边建图，对搜索出的亮灯方案使用并查集判断点亮的灯管是否在同一个集合。

推荐一篇并查集的文章:算法学习笔记(1) : 并查集 - 知乎

 代码:

#include <iostream>
#include <cstring>
using namespace std;
 
const int MAXN = 25;
int n = 7, ans = 0, path[MAXN], f[MAXN][MAXN], father[MAXN];
 
//查找 x 的祖先节点
int find(int x)
{
    if (x != father[x]) { //路径压缩
        return father[x] = find(father[x]);
    }
    return father[x];
}
 
void dfs(int u, int p, int m)
{
    if (u == m) {
        //初始化操作
        for (int i = 1; i < MAXN; ++i) {
            father[i] = i;
        }
        //集合合并
        for (int i = 0; i < m; ++i) {
            for (int j = i + 1; j < m; ++j) {
                //存在边相连
                if (f[path[i]][path[j]] == 1) {
                    //path[i] 和 path[j] 合并成一个集合
                    father[find(path[i])] = find(father[path[j]]);
                }
            }
        }
        //查找最终是否为一个集合
        bool flag = false;
        for (int i = 0; i < m - 1; ++i) {
            if (find(path[i]) != find(path[i + 1])) {
                flag = true;
                break;
            }
        }
 
        if (!flag) {
            ++ans;
        }
        return ;
    }
    for (int i = p; i <= n; ++i) {
        path[u] = i;
        dfs(u + 1, i + 1, m);
    }
}
 
int main()
{
    memset(f, 0, sizeof(f));
    f[1][2] = f[2][1] = 1;
    f[1][6] = f[6][1] = 1;
    f[2][7] = f[7][2] = 1;
    f[6][7] = f[7][6] = 1;
    f[7][3] = f[3][7] = 1;
    f[7][5] = f[5][7] = 1;
    f[2][3] = f[3][2] = 1;
    f[3][4] = f[4][3] = 1;
    f[4][5] = f[5][4] = 1;
    f[5][6] = f[6][5] = 1;
    for (int i = 1; i <= n; ++i) {
        dfs(0, 1, i);
    }
    cout << ans << endl;
    return 0;
}

答案:80 

跑步锻炼

思路:经典的日期问题, 细心点写,注意瑞年的判断和每个月的月数,就没啥大问题。

代码

#include<iostream>
using namespace std;
//2000 1 1(星期六)-2020 10 1
/**/
int ants = 0;
int Month[13] = { 0,31,28,31,30,31,30,31,31,30,31,30,31 };
int main()
{
	int year = 2000, month = 1, day = 1, weekday = 6;
	while (1)
	{
		ants += (weekday == 1 || day == 1) + 1;//判断是否是星期一或者是每个月月初
		if (year == 2020 && month == 10 && day == 1)//结束条件
		{
			break;
		}
		//星期循环，和天数增加
		day += 1;
		weekday = (weekday + 1) % 7;
		//判断是否是瑞年并且是二月份
		if (month == 2 && (year % 4 == 0 && year % 100 != 0 || year % 400 == 0))
		{
			if (day > Month[month] + 1)
			{
				day = 1;
				month += 1;
			}
		}
		else if (day > Month[month])
		{
			day = 1;
			month += 1;
		}
		if (month == 13)
		{
			month = 1;
			year += 1;
		}
 
	}
	cout << ants << endl;
	return 0;
}

 答案:8879

 回文日期

 输入样例

2
20200202
20211203

输出样例

20211202
21211212
20300302
21211212

思路: 这道题需要用字符串和数字之间的转换,然后判断一个日期是否是回文串,日期是否合法,在前面的基础上再判断是否是ABBABABA,对思维要求不高,基本都能想出来,就是代码量和操作有点繁琐.我们先练习下字符串和数字之间的来回转化，这个要掌握,竞赛中经常用到

/*1.数字转换成字符串*/
	int num = 123;
	stringstream ss;
	ss << num;
	string  s = ss.str();
	cout << s << endl;

    /*2.字符串转换成数字*/
	string s1 = "123";
	int num1 = atoi(s1.c_str());
     cout << num1 << endl;
	/*3.字符串转换成数字*/
	string s2 = "456";
	stringstream ss2;
	ss2 << s2;
	int num2;
	ss2 >> num2;
	cout << num2 << endl;

代码

#include<iostream>
#include<set>
#include<sstream>
#include<string>
#include<algorithm>
using namespace std;
/*如何判断一个日期是否是回文串
日期是否合法?
在1,2的基础上如何判断该日期是ABBA BABA型的回文日期?*/
//run[0]表示的是瑞年每个月的天数;run[1]表示的是非瑞年每个月的天数
int run[2][13] = { {0,31,29,31,30,31,30,31,31,30,31,30,31},{0,31,28,31,30,31,30,31,31,30,31,30,31} };
//2121 12 12      //长度为8
//0123 45 67下标  //if(s[1]!=s[6]) i=1,6=len-i--1;
bool fun(string s)//判断是否为回文日期
{
	for (int i = 0; i < s.length(); i++)
	{
		if (s[i] != s[s.length() - i - 1])return false;
	}
	//判断日期是否合法
	int y = (s[0] - '0') * 1000 + (s[1] - '0') * 100 + (s[2] - '0') * 10 + (s[3] - '0');
	int m = (s[4] - '0') * 10 + (s[5] - '0');
	int d = (s[6] - '0') * 10 + (s[7] - '0');
	if (m > 12)return false;
	int f = (y % 4 == 0 && y % 100 != 0) || (y % 400 == 0)?0:1;
	if (d > run[f][m])return false;
	return true;
}
bool fun2(string s)//判断是否为ABAB BABA型的回文日期
{
//ABAB BABA型的字符串只有两个不同的元素———>set,求不同元素的个数
	set<char> st;
	for (int i = 0; i < s.length(); i++)
	{
		st.insert(s[i]);
	}
	if (st.size() != 2)return false;
	//只有两个不同元素的回文日期的情况;
	/*
	* 1.AABB BBAA
	* 2.ABAB BABA
	* 3.ABAA AABA
	* 4.ABBB BBBA
	* 要得到2
	*/
	if (s[0] == s[1] || s[2] == s[3])return false;//直接排除
	return true;
 
}
int main()
{
	string s;
	cin >> s;
	stringstream tmp;
	tmp << s;
	long long num;
	tmp >> num;
	int f1 = 0;//表示没有找到回文日期
	int f2 = 0;//表示没有找到ABAB BABA型的回文日期
	for (long long i = num+1; i <= 89991231; i++)
	{
		if (f1 == 1 && f2 == 1)break;//表示已经得到最后的结果
		//把日期先转换成字符串
		stringstream t2;
		t2 << i;
		string S = t2.str();
		if (fun(S) == false)continue;//不是回文日期，跳过该循环
		//确保了字符串S是回文日期
		if (f1 == 0)
		{
			cout << S << endl;
			f1 = 1;
		}
		if (fun2(S) == true)//ABABBABA型的回文日期
		{
			cout << S << endl;
			f2 = 1;
		}
	}
	return 0;
}

字串排序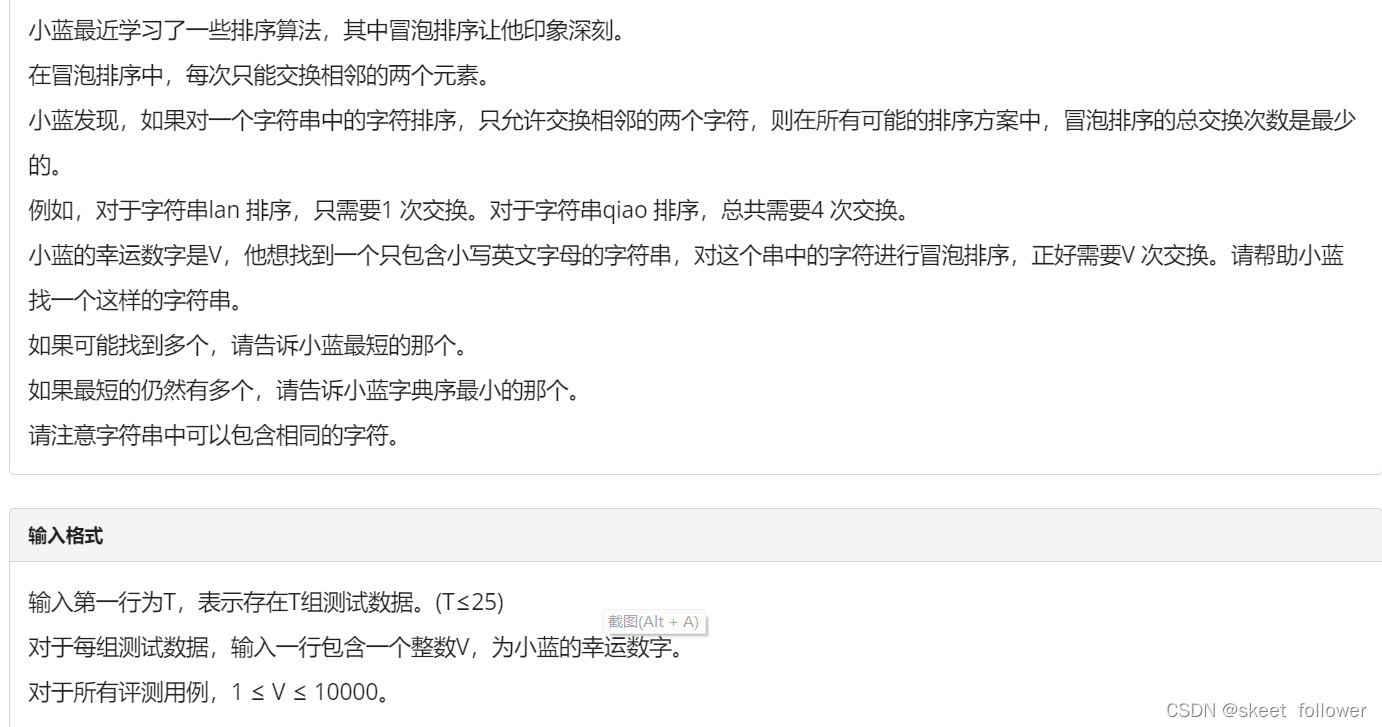
 

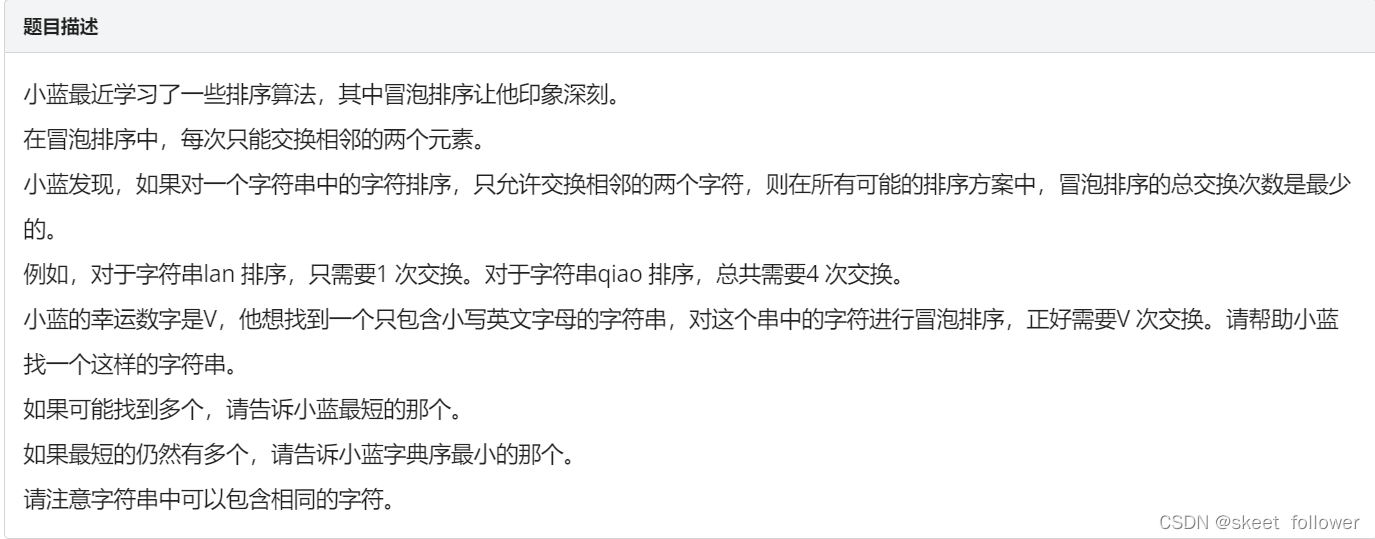
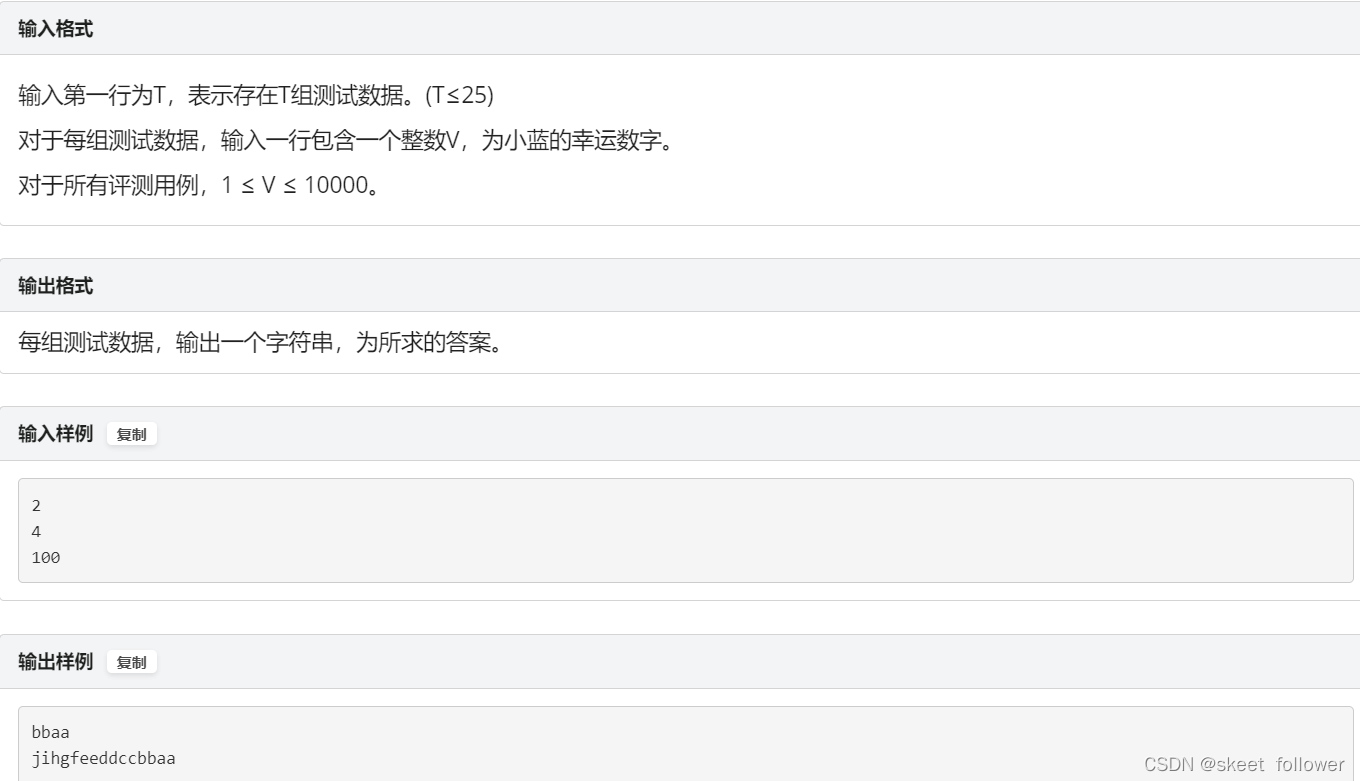
 思路:这道题看的我迷迷瞪瞪,我在网上找了很多参考答案,给大家推荐一篇博客:

蓝桥杯“字串排序“题解_Nervous_46216553的博客-CSDN博客_蓝桥杯字串排序

代码:

import java.util.Scanner;
public class Main {
	static int list[]={//存放后缀序列，这样插和删除很容易
		0,0,0,0,0,//注cccbba=1,2,3,0,……
		0,0,0,0,0,
		0,0,0,0,0,
		0,0,0,0,0,
		0,0,0,0,0,
		0
	};
	static int[] str=new int[300];//存放前缀序列
	static void reset() {//后缀序列清零
		int i=0;
		while(i<26&&list[i]!=0) {
			list[i]=0;
			++i;
		}
	}
	static int getrnum() {//计算逆序数（分三步）
		int cnt=0;
		for(int i=0;str[i]!=0;++i) {//前缀的逆序数
			for(int j=i;str[j]!=0;++j) {
				if(str[i]>str[j]) {
					++cnt;
				}
			}
		}
		for(int i=0;str[i]!=0;++i) {//前缀对后缀的逆序数
			for(int j=25;j>=0;--j) {
				if(str[i]-'a'>j) {
					cnt+=list[j];
				}
			}
		}
		int temp=0;
		for(int i=0;i<26;++i) {//后缀的逆序数
			cnt+=temp*list[i];
			temp+=list[i];
		}
		return cnt;
	}
	static int getinc(int c) {//获得最大逆序增量（特殊步骤中代替求逆序数函数用来提速）（可以认为在数字符串里有多少非c(传入的参数)字符）(也就是插入c逆序数能增加多少)
		int i=0,cnt=0;
		while(str[i]!=0) {
			if(str[i]>(c+'a')) {
				cnt++;
			}
			++i;
		}
		for(i=0;i<26;++i) {
			if(i!=c) {
				cnt+=list[i];
			}
		}
		return cnt;
	}
	static void set() {//在后部序列中插入元素，保证逆序数最大
		int max=0,temp=0,index=0;
		for(int i=0;i<26;++i) {
			list[i]++;
			if((temp=getinc(i))>max) {//找出使逆序数增得最快的字符插入（这里比用增而直接记录逆序数不影响结果，但慢一些，数据10000左右要5秒左右，会超时的，不然我也不会编这么个对于的函数。。）
				index=i;
				max=temp;
			}
			list[i]--;
		}
		list[index]++;
	}
	static void getMaxStr(int l) {//获取前缀确定且长度确定的前提下的最大逆序数字串
		reset();
		for(int i=0;str[i]!=0;++i,--l);
		while(l>0) {
			set();
			--l;
		}
	}
	static void printstr() {//打印目标字符串
		String Str="";
		int i=0;
		while(str[i]!=0) {
			Str+=(char)str[i];
			++i;
		}
		for(i=25;i>=0;--i) {//这里其实没用，既然不执行也不会影响效率，留着吧，后缀最后是空的，但曾经存在过。。。
			for(int j=0;j<list[i];++j) {
				Str+=(char)(i+'a');
			}
		}
		System.out.println(Str);
	}
	static void getans(int num,int l) {//l是字串长度
		for(int i=0;i<l;++i) {
			for(int j=0;j<26;++j) {//每个位从a开始试
				str[i]=j+'a';
				getMaxStr(l);//获取指定前缀最大逆字串
				if(getrnum()>=num) {//超了就下一个
					break;
				}
			}
		}
	}
	public static void main(String[] args){//这了很简洁了
		int num;
		Scanner sc = new Scanner(System.in);
		num=sc.nextInt();//获取输入
		sc.close();
		int l=0;
		while(getrnum()<num) {//获取最短字串长
			++l;
			getMaxStr(l);
		}
		getans(num,l);//获得目标字串
		printstr();//打印
	}
}

成绩统计

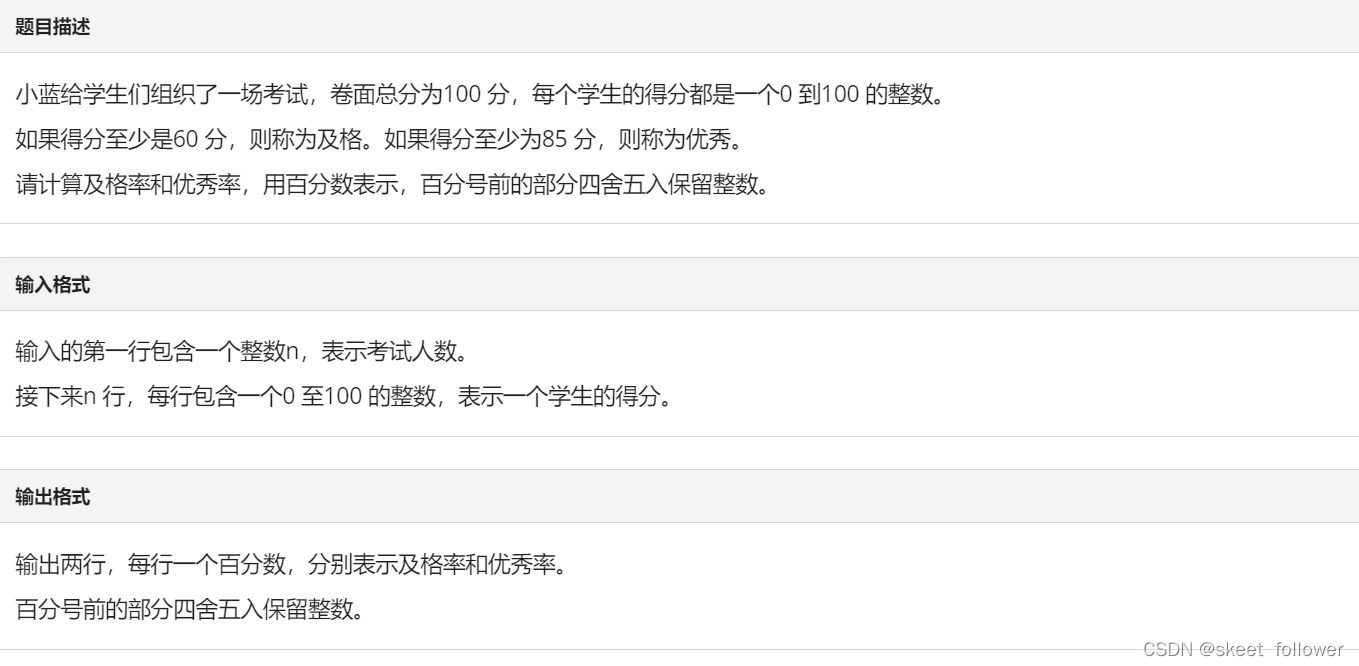
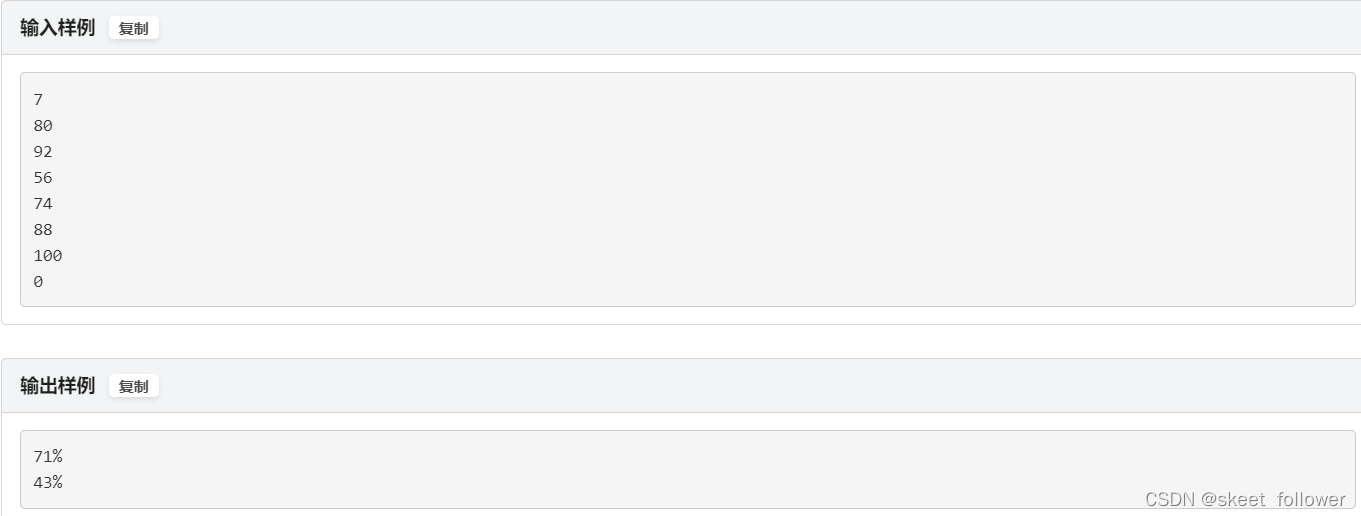
我严重怀疑这个网站给的题目顺序不对,前面编程题越做越吃劲,怎么越往后越容易

代码

#include <iostream>
using namespace std;
int main()
{
    double a = 0;
    double b = 0;
    double c;
    cin >> c;
    int n;
    for (int i = 0; i < c; i++)
    {
        cin >> n;
        if (n >= 60)
        {
            a++;
        }
        if (n >= 85)
        {
            b++;
        }
 
    }
    int x =(a * 100.0)/c+0.5;
    int y =(b * 100.0)/c+0.5;
    cout << x << "%" << endl << y << "%";
    return 0;
}

子串分值和

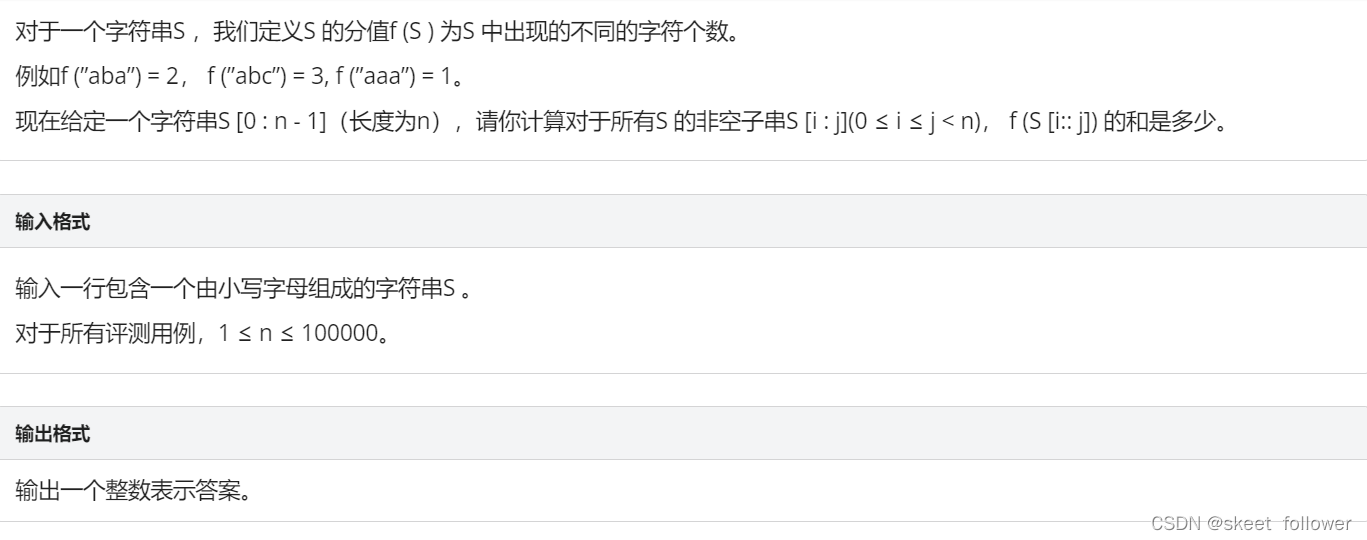
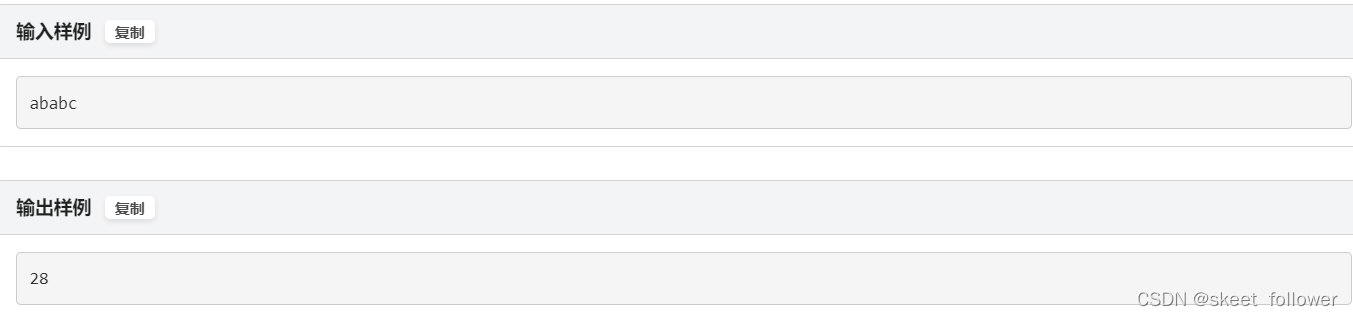
 代码

#include<iostream>
#include<cstring>
using namespace std;
typedef long long LL;
int num[26]; //某字母在字符串中上一次出现的位置
int main() {
    string s;
    cin >> s;//ababc
    int len = s.size();//5
    memset(num, -1, sizeof(num));//初始化为-1
    LL ans = 0;
    for (int i = 0; i < len; ++i) {
        ans += (LL)(i - num[s[i] - 'a']) * (len - i);
        num[s[i] - 'a'] = i;
    }
    printf("%lld\n", ans);
    return 0;
}

平面切分

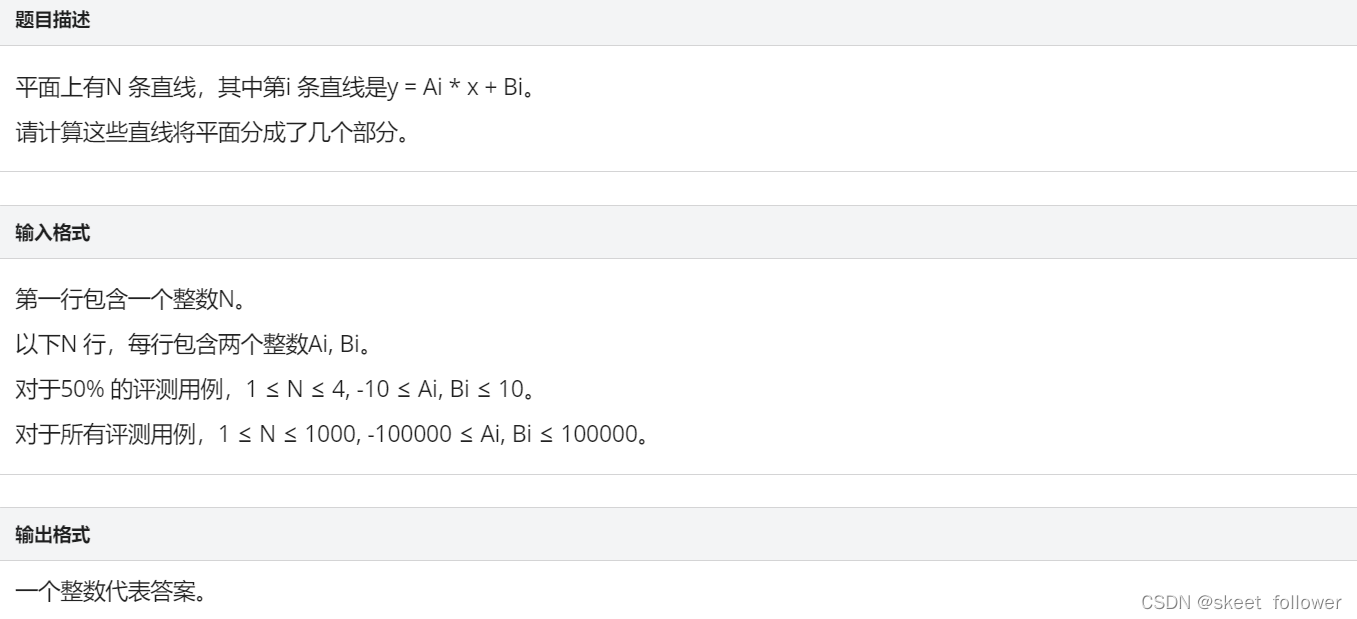
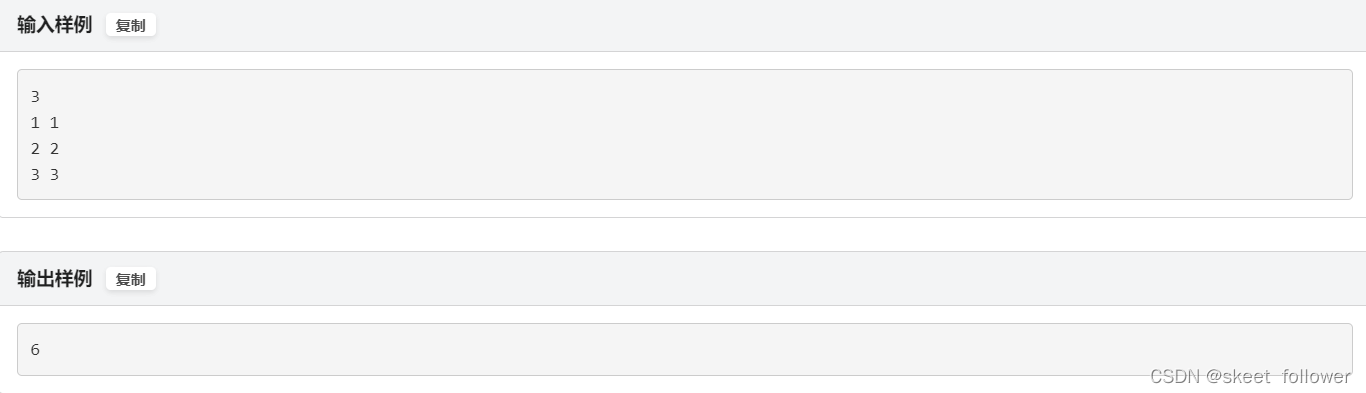
思路:推荐博客蓝桥杯:平面切分_fa2000_12_16的博客-CSDN博客_蓝桥杯平面切分

代码

#include<bits/stdc++.h>
using namespace std;
const int N = 1005;
 
int main()
{
	int n;
	scanf("%d", &n);
	int a, b;
	long double A[N], B[N];
	pair<long double, long double> p; 
	set<pair<long double, long double> > s;  //利用set自动去重功能筛选掉重边 
	for(int i = 0; i < n; i++)
	{
		scanf("%d %d", &a, &b);
		p.first = a;
		p.second = b;
		s.insert(p);
	}
	int i = 0;  //将去重后的直线数据放回A,B数组 
	for(set<pair<long double, long double> >::iterator it = s.begin(); it != s.end(); it++, i++)
	{
		A[i] = it -> first;
		B[i] = it -> second;
	}
	long long ans = 2;  //初始情况当只有一条直线时，有两个平面 
	for(int i = 1; i < s.size(); i++)  //从下标1开始，也就是第二条直线 
	{
		set<pair<long double, long double> > pos;  //记录第i条直线与先前的交点 
		for(int j = i-1; j >= 0; j--)
		{
			int a1 = A[i], b1 = B[i];
			int a2 = A[j], b2 = B[j];
			if(a1 == a2)  //遇到平行线无交点，跳出 
				continue; 
			p.first = 1.0*(b2-b1)/(a1-a2);
			p.second = 1.0*a1*((b2-b1)/(a1-a2)) + b1;
			pos.insert(p); 
		}
		ans += pos.size() + 1;  //根据结论，每增加一条直线，对平面数的贡献值是其与先前直线的交点数（不重合）+1 
	} 
	printf("%d\n", ans);
	return 0;
}