蚁群算法在路径规划中的应用_蚁群算法excel

一、蚁群算法的概述：

蚁群算法（AG）于1991年由M.Dorigo等人首先提出，是一种以种群寻优为基础的启发式搜索算法。基础原理是利用蚂蚁种群间简单的生物信息传递，通过正反馈、分布式协作来搜索从蚁巢到食物间最短距离的寻优方式。

蚁群算法将全局优化、有限时间内答案的合理性以及寻优的快速性相结合，得到众多学者的青睐，基础模型也在不断地得到改进和拓展。其中，求解的快速性是由具有正反馈效应信息的传递和积累保证的。同时，该算法早熟性收敛的缺电可以通过分布式计算的特征来加以避免，而且，具有贪婪特征的启发式搜索蚁群系统还能够在搜索过程早期就找到可以接受的问题解。

二、蚁群算法流程

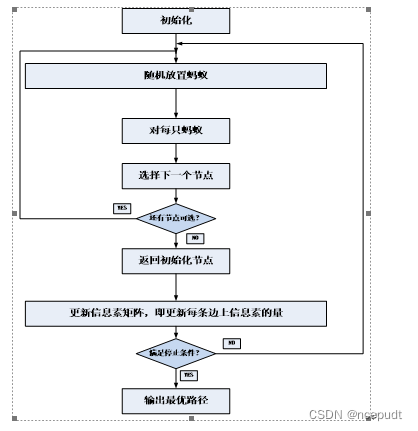
 三、路径规划问题

路径优化问题，根据起始点与终点的不同以及运输线路的不同，可以分为多点间运输问题、点对点运输问题、单回路运输问题和多回路运输问题。多点间的运输问题可以定义为一个运输调配的线性规划问题，即不同起始点与终点的匹配问题；点对点运输问题可以看作最短路径问题，即寻求两点间最短的通过路径；单回路运输问题又叫做旅行商问题（TSP），即求解从起始点出发，访问每一个点一次，并回到起始点的最短回路；多回路运输问题即车辆路径问题（VRP）——在满足一定约束条件（时间约束、载重约束、距离越数等）的情况下，对于一系列的装货和卸货点，规划行车路径，从而达到最优目标。其中，点对点运输问题是路径优化问题的基础，车辆路径问题则是该领域研究的重点和热点。

四、蚁群算法解决路径规划问题

function [R_best,L_best,L_ave,Shortest_Route,Shortest_Length]=ANT_VRP(D,Demand,Cap,iter_max,m,Alpha,Beta,Rho,Q)
 
%% R_best 各代最佳路线
%% L_best 各代最佳路线的长度
%% L_ave 各代平均距离
%% Shortest_Route 最短路径
%% Shortest_Length 最短路径长度
%% D 城市间之间的距离矩阵，为对称矩阵
%% Demand 客户需求量
%% Cap 车辆最大载重
%% iter_max 最大迭代次数
%% m 蚂蚁个数
%% Alpha 表征信息素重要程度的参数
%% Beta 表征启发式因子重要程度的参数
%% Rho 信息素蒸发系数
%% Q 信息素增加强度系数
 
n=size(D,1);                 
T=zeros(m,2*n);           %装载距离
Eta=ones(m,2*n);          %启发因子
Tau=ones(n,n);            %信息素
Tabu=zeros(m,n);          %禁忌表
Route=zeros(m,2*n);       %路径
L=zeros(m,1);             %总路程
L_best=zeros(iter_max,1);   %各代最佳路线长度
R_best=zeros(iter_max,2*n); %各代最佳路线
nC=1;
 
while nC<=iter_max                   %停止条件
    Eta=zeros(m,2*n);   
    T=zeros(m,2*n);  
    Tabu=zeros(m,n);
    Route=zeros(m,2*n);
    L=zeros(m,1);
    
    %%%%%%==============初始化起点城市（禁忌表）====================
    for i=1:m
        Cap_1=Cap;      %最大装载量
        j=1;
        j_r=1;
        while Tabu(i,n)==0
             T=zeros(m,2*n);    %装载量加载矩阵
             Tabu(i,1)=1;       %禁忌表起点位置为1
             Route(i,1)=1;      %路径起点位置为1
             visited=find(Tabu(i,:)>0);   %已访问城市
             num_v=length(visited);        %已访问城市个数
             J=zeros(1,(n-num_v));         %待访问城市加载表
             P=J;                          %待访问城市选择概率分布
             Jc=1;                         %待访问城市选择指针
             for k=1:n                     %城市
                 if length(find(Tabu(i,:)==k))==0    %如果k不是已访问城市代号，就将k加入矩阵J中
                     J(Jc)=k;
                     Jc=Jc+1;
                 end
             end
             
           %%%%%%%=============每只蚂蚁按照选择概率遍历所有城市==================
             
             for k=1:n-num_v               %待访问城市
                 
                   if Cap_1-Demand(J(1,k),1)>=0    %如果车辆装载量大于待访问城市需求量
 
                     if Route(i,j_r)==1           %如果每只蚂蚁在起点城市
                         T(i,k)=D(1,J(1,k));
                         P(k)=(Tau(1,J(1,k))^Alpha)*((1/T(i,k))^Beta);  %概率计算公式中的分子
                     else                         %如果每只蚂蚁在不在起点城市
                         T(i,k)=D(Tabu(i,j),J(1,k));
                         P(k)=(Tau(Tabu(i,visited(end)),J(1,k))^Alpha)*((1/T(i,k))^Beta); %概率计算公式中的分子
                     end
                     
                 else              %如果车辆装载量小于待访问城市需求量
                     T(i,k)=0;
                     P(k)=0;
                 end
             end
             
             
             if length(find(T(i,:)>0))==0    %%%当车辆装载量小于待访问城市时，选择起点为1
                 Cap_1=Cap;
                 j_r=j_r+1;
                 Route(i,j_r)=1;              
                 L(i)=L(i)+D(1,Tabu(i,visited(end)));   
             else
                 P=P/(sum(P));                 %按照概率原则选取下一个城市
                 Pcum=cumsum(P);               %求累积概率和：cumsum（[1 2 3])=1 3 6,目的在于使得Pcum的值总有大于rand的数
                 Select=find(Pcum>rand);       %按概率选取下一个城市：当累积概率和大于给定的随机数，则选择求和被加上的最后一个城市作为即将访问的城市
                 o_visit=J(1,Select(1));       %待访问城市
                 j=j+1;
                 j_r=j_r+1;
                 Tabu(i,j)=o_visit;             %待访问城市
                 Route(i,j_r)=o_visit;
                 Cap_1=Cap_1-Demand(o_visit,1);  %车辆装载剩余量
                 L(i)=L(i)+T(i,Select(1));       %路径长度
             end
        end
         L(i)=L(i)+D(Tabu(i,n),1);               %%路径长度
    end
    
    L_best(nC)=min(L);             %最优路径为距离最短的路径
    pos=find(L==min(L));           %找出最优路径对应的位置：即为哪只蚂蚁
    R_best(nC,:)=Route(pos(1),:);  %确定最优路径对应的城市顺序
    L_ave(nC)=mean(L)';            %求第k次迭代的平均距离
    
    Delta_Tau=zeros(n,n);            %Delta_Tau(i,j)表示所有蚂蚁留在第i个城市到第j个城市路径上的信息素增量
    L_zan=L_best(1:nC,1);
    post=find(L_zan==min(L_zan));
    Cities=find(R_best(nC,:)>0);
    num_R=length(Cities);
    
    for k=1:num_R-1          %建立了完整路径后在释放信息素
        Delta_Tau(R_best(nC,k),R_best(nC,k+1))=Delta_Tau(R_best(nC,k),R_best(nC,k+1))+Q/L_best(nC);
    end
        Delta_Tau(R_best(nC,num_R),1)=Delta_Tau(R_best(nC,num_R),1)+Q/L_best(nC);
        Tau=Rho*Tau+Delta_Tau;
        
        nC=nC+1;
end
Shortest_Route=zeros(1,2*n);           %提取最短路径
Shortest_Route(1,:)=R_best(iter_max,:);
Shortest_Route=Shortest_Route(Shortest_Route>0);
Shortest_Route=[Shortest_Route Shortest_Route(1,1)];
Shortest_Length=min(L_best);           %提取最短路径长度
%L_ave=mean(L_best);

以上为蚁群算法求解程序，单独保存为.m文件,命名ANT_VRP，以供调用。具体求解示例如下：

clc;clear all
%% ==============提取数据==============
[xdata,textdata]=xlsread('shili.xlsx'); %加载20个城市的数据，数据按照表格中位置保存在Excel文件exp12_3_1.xls中
x_label=xdata(:,2); %第二列为横坐标
y_label=xdata(:,3); %第三列为纵坐标
Demand=xdata(:,4);  %第四列为需求量
C=[x_label y_label];      %坐标矩阵
n=size(C,1);        %n表示节点（客户）个数
%% ==============计算距离矩阵==============
D=zeros(n,n);       %D表示完全图的赋权邻接矩阵，即距离矩阵D初始化
for i=1:n
   for j=1:n
       if i~=j
           D(i,j)=((C(i,1)-C(j,1))^2+(C(i,2)-C(j,2))^2)^0.5; %计算两城市之间的距离
       else
           D(i,j)=0;   %i=j, 则距离为0；
       end
       D(j,i)=D(i,j);  %距离矩阵为对称矩阵
   end
end
Alpha=1;Beta=5;Rho=0.75;iter_max=100;Q=10;Cap=1;m=20;  %Cap为车辆最大载重
[R_best,L_best,L_ave,Shortest_Route,Shortest_Length]=ANT_VRP(D,Demand,Cap,iter_max,m,Alpha,Beta,Rho,Q); %蚁群算法求解VRP问题通用函数，详见配套光盘
Shortest_Route_1=Shortest_Route-1    %提取最优路线
Shortest_Length                      %提取最短路径长度
 
%% ==============作图==============
figure(1)   %作蚂蚁迭代曲线图
x=linspace(0,iter_max,iter_max);
y=L_best(:,1);
plot(x,y);
xlabel('迭代次数'); ylabel('最短路径长度');
 
figure(2)   %作最短路径图
plot([C(Shortest_Route,1)],[C(Shortest_Route,2)],'o-');
grid on
for i =1:size(C,1)
    text(C(i,1),C(i,2),['   ' num2str(i-1)]); 
end
xlabel('客户所在横坐标'); ylabel('客户所在纵坐标');

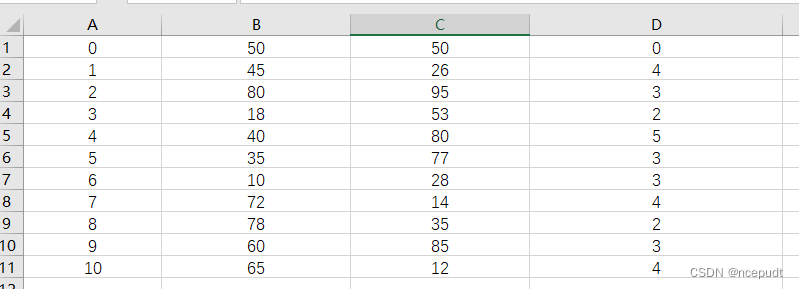
其中，示例excel文件如下，每一行依次为序号、横坐标、纵坐标、需求量，第一行为配送中心。