- 1Android 蓝牙开发(二) --手机与蓝牙音箱配对,并播放音频_android 蓝牙耳机接受音频
- 2【链表经典面试题保姆级题解】什么?这八个最基本的链表面试题你还没有掌握?最短的时间内教会你!_链表为空怎么解决
- 3绕过Cloudflare五秒盾,穿云API抓取网页不再等待_五秒盾会检测ip吗
- 4UnicodeDecodeError: ‘utf-8‘ codec can‘t decode byte 0xd2 in position 422: invalid continuation byte_syntaxerror: (unicode error) 'utf-8' codec can't d
- 5基于yolov5的苹果成熟度检测系统,可进行图像目标检测,也可进行视屏和摄像检测(pytorch框架)【python源码+UI界面+功能源码详解】_基于yolo的苹果成熟度识别
- 6第18届全国大学生智能汽车竞赛四轮车开源讲解【12】--写在最后_江科大智能小车
- 7什么是Kafka?有什么主要用途?_kafka作用
- 8java审批流创建及代码流程
- 9【记录】pip install git+https://github.com/XXX/XXX 报错
- 10整型提升和算术转换<C语言>
python期末简答题及答案,python期末题库和答案_python期末老师问问题
赞
踩
大家好,小编来为大家解答以下问题,python期末简答题及答案,python期末题库和答案,今天让我们一起来看看吧!

Python期末复习资料
目录
例题1、输出songs中出现最多的一个中文字,并输出该字出现次数
from math import *
| math.fabs(x) | 返回 x 的绝对值 |
| math.factorial(x) | 以一个整数返回 x 的阶乘,如果 x 不是整数或为负数时则将引发 ValueError |
| math.floor(x) | 返回 x 的向下取整,小于或等于 x 的最大整数 |
| math.ceil(x) | 返回 x 的向上取整,即大于或者等于 x 的最小整数。 |
| math.gcd(a, b) | 返回整数 a 和 b 的最大公约数 |
| math.exp(x) | 返回 e 次 x 幂,其中 e = 2.718281… 是自然对数的基数 |
| math.log(x[, base]) | 使用两个参数,返回给定的 base 的对数 x ,计算为 log(x)/log(base) |
| math.hypot(x, y) | 返回欧几里德范数, sqrt(x*x + y*y) 用python画雪人。 这是从原点到点 (x, y) 的向量长度 |
| math.acos(x) | 以弧度为单位返回 x 的反余弦值 |
| math.radians(x) | 将角度 x 从度数转换为弧度。 |
| math.fibonacci(x) | 生成斐波那契数列 |
| 描述 | \n | 换行 | |
| \(在行尾时) | 续行符 | \v | 纵向制表符 |
| \\ | 反斜杠符号 | \t | 横向制表符 |
| \’ | 单引号 | \r | 回车 |
| \" | 双引号 | \f | 换页 |
| \a | 响铃 | \oyy | 八进制数yy表示的字符,例如:\o12代表换行 |
| \b | 退格(backspace) | \xyy | 十六进制数yy表示的字符,例如:\x0a代表换行 |
| \e | 转义 | \other | 其他字符以普通格式输出 |
| \000 | 空 |
| %o | 八进制整数 |
| %x | 十六进制整数 |
| %d | 十进制整数 |
| %i | 整数 |
| %f | 保留小数点后面六位有效数字 |
| %.3f | 保留3位小数位 |
| %e | 保留小数点后面六位有效数字,指数形式输出 |
| %.3e | 保留3位小数位,使用科学计数法 |
| %g | 在保证六位有效数字的前提下,使用小数方式,否则使用科学计数法 |
| %.3g | 保留3位有效数字,使用小数或科学计数法 |
| % | 取模 - 返回除法的余数 |
| ** | 幂 - 返回x的y次幂 |
| // | 取整除 - 向下取接近商的整数 |
def f(x,y):
return ……
f=lambda x,y:x+y
f=lambda x:if ……else y
if:
……
elif:
……
else:
……
- For循环
for i in range(start,stop,step)/str/list:
……
- While 循环
while True/条件:
循环语句
- if...break/continue的意思是如果满足了某一个条件,就提前结束/(本次)循环
for i in range(5):
print('明日复明日')
if i==3: # 当i等于3的时候触发
break # 结束循环
for i in range(5):
print('明日复明日')
if i==3: # 当i等于3的时候触发
continue # 跳过该次循环
- 循环语句可以有 else 子句,它在穷尽列表(以for循环)或条件变为 false (以while循环)导致循环终止时被执行,但循环被 break 终止时不执行
for i in range(5):
a = int(input('请输入0来结束循环,你有5次机会:'))
if a == 0:
print('你触发了break语句,循环结束,导致else语句不会生效。')
break
else:
print('5次循环你都错过了,else语句生效了。')

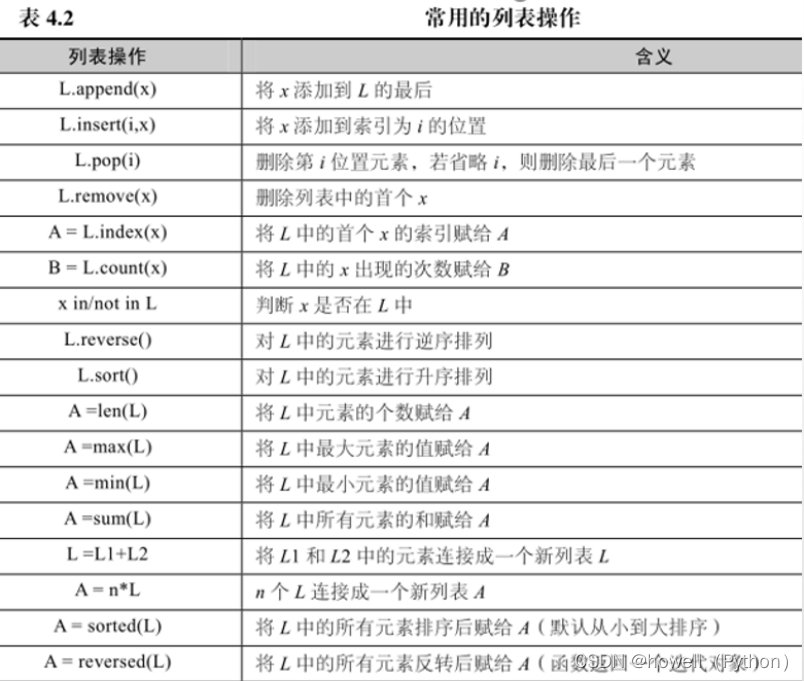
| s.find(substr,[start:[end]]) | 返回 substr串在s串中的第一个字符的下标, start和 end表示查找的范围,没有找到返回-1 |
| s.index(substr,[start:[end]]) | 用法同s.find()相同,substr不在返回则会报异常 |
| s.count(str,[start=0,end=len(s))]) | 返回 str 在 s 里面出现的次数,如果 start 或者 end 指定则返回指定范围内 str 出现的次数 |
| s.replace(oldstr,newstr,[count]), | 用newstr替换oldstr,,count为替换次数 |
| s.split([sep,[maxsplit]) | 以sep为分隔符,把字符串s拆分为一个列表,默认的以空格作为分隔符 |
| s.strip([chars]) s.lstrip() s.rstrip() | 删除s前后[chars]字符串,默认是删除首尾空格 删除s左边前后[chars]字符串,默认是删除左边空格 删除s右边前后[chars]字符串,默认是删除右边空格 |
| s.join(seq) | 把seq代表的序列组合成字符串,用s将序列各元素连接起来 |
| ord(str) | 将一个字符转换为它的整数值 |
| chr(x) | 将一个整数转换为一个字符 |
| for s in reversed(str5): print(s,end=‘ ‘) | 对字符串中的元素逆序输出 |
| for i,ch in enumerate(str5): print(i,ch) | 提取序列元素的下标与值 |
例题1、输出songs中出现最多的一个中文字,并输出该字出现次数
songs=input()#仅包含空格和中文字
#1. 输出songs中出现最多的一个中文字,并输出该字出现次数。
#注意:如果有多个字出现次数相同,请以原文本中最先出现的那个为准。
result=[]
num=[]
for word in songs:
if word!=' 'and word not in result:
result.append(word)
for word in result:
num.append(songs.count(word))
maxV=max(num)
maxindex=num.index(maxV)
print(result[maxindex],maxV)
def printYanghui(num):
list1=[1] #定义一个列表用来储存上一行
print(1) #输出第一行1
for i in range(2,num+1): #循环输出2~num行
row=[1] #定义列表行
# print(1,end=' ') #输出每行第一个1
for j in range(0,i-2): #第i行应有i个元素,中间有i-2个元素
row.append(list1[j]+list1[j+1]) #插入上一行的两两元素和
row.append(1) #补上末尾的1
print(row)
list1=row
printYanghui(int(input()))
for i in nameList:
a = str(i)
if "王" in a:
b=nameList.index(i)
nameList[b]="王仁"
break
(1)字典(dict)的基本操作:创建
scores = {'小明': 95, '小红': 90, '小刚': 90}
dictname = dict.fromkeys(list,value=None)
(2)字典(dict)的访问:通过键来访问对应的值
dictname[key]
dictname.get(key[,default])
- 字典的删除
del dictname[]
- 添加键值对
a[‘语文’]=90
(5)dict方法集
keys() 方法用于返回字典中的所有键(key)
values() 方法用于返回字典中所有键对应的值(value)
items() 用于返回字典中所有的键值对(key-value)
从键盘输入一串字符,统计字符串中出现次数最多的单词和次数,如果有多个相同的最多次数,需要输出多个单词及次数。
#输入的字符串中可包含".,~!@#$%^&*()+_/0123456789"等非英文单词字符
WordStr = input()
#stpe1:归一化处理
WordStr=WordStr.lower()
for ch in ".,~!@#$%^&*()+_/0123456789":
WordStr=WordStr.replace(ch," ")
#2分割字符串为列表,英文单词之间用空格分隔
Wordlist=WordStr.split(" ")
#3 统计每个单词的个数(列表或字典的方法)
Worddict={}
for word in Wordlist:
if word in Worddict and word !="":
Worddict[word]+=1
elif word not in Worddict and word !='':
Worddict[word]=1
#字典排序,返回值是一个列表
lis1=sorted(Worddict.items(),key=lambda x:x[1],reverse=True)
#输出最高频率单词和次数 ,多个相同高频字也要输出
for i in range(len(lis1)):
if lis1[i][1]==lis1[0][1]:
print(lis1[i][0],lis1[i][1])
f = open(file, mode='r', encoding=None)



(1)dataframe创建
从字典创建dataframe:
data = {'state': ['Ohio', 'Ohio', 'Ohio', 'Nevada', 'Nevada'], 'year': [2000, 2001, 2002, 2001, 2002], 'pop': [1.5, 1.7, 3.6, 2.4, 2.9]}
df=pd.DataFrame(data)
读取excel、csv、txt文件:
import pandas as pd
df = pd.read_excel('example.xls',header=None,nrows = 5) #header为索引列
df = pd.read_csv('example.csv',encoding = 'gbk')
df = pd.read_table('example.txt',encoding = 'gbk',sep = ',',nrows= 5)#nrow为读取行数
df.to_excel('example_new.xlsx',index = False,encoding = "utf-8")
1.按列索引
df['性别'] or df.性别 #访问某一列数据
df[['性别','消费金额']] #访问不连续的多列数据
df['性别':'消费金额'] #访问连续的多列数据
2.按行索引
df.loc[‘onr’:’three’]
df.iloc[0:3]
3.按行、列索引
df.loc[1:3,'性别':'消费金额']
df.iloc[[1,3],[1,3]]
4.布尔索引
df[df['消费金额']>=300] #消费金额>300的行
添加
df=df.append({'year':2003,'state':'Louisiana','pop':1.4},ignore_index=True)#行
df['total']=0 #列
df['total']=df['pop']-df['debt'] #先将debt列值设为1
删除
df.drop(5,inplace=True) #行
df.drop(‘debt’,axis=1,inplace=True) #列
修改
#获取和修改列类型:
df['pop'].dtype
df['pop']=df['pop'].astype(str)
#修改值
df['pop']=df['pop']+3
df.loc[df['year']>=2002,'pop'] +=1
排序
df.sort_values(by=['pop'],ascending=True)
df.sort_values(by=['year','pop'],ascending=False)
df.sort_values(by=[‘year’,’pop’],ascending=[False,True]):year按降序,Pop按升序排序
合并数据集
df3=pd.concat([df1,df],ignore_index=True) #首先df1=df.copy()
df3=pd.concat([df1,df], axis=1) #轴1方向拼接
lambda函数
df['height_grade']=df['height'].apply(lambda x:'high' if x>=1.7 else 'short' if x<1.6 else 'middle')
A.arr函数创建
import numpy as np
data1 = [[6, 7.5, 8, 0, 1], [3.2, 3, 7, 52, 23.4]]
arr1 = np. array( data1)
arr1 = arr1.reshape(2,3) #改变为:2行3列的二维数组
B.生成数组
创建初始值为0,终值为1,步长为0.1的等差数组
np.arange(0, 1, 0.1)
创建初始值为0,终值为1,元素个数为10的等差数组
np.linspace(0, 1,10) # 步长为 1/9,lin是linear的缩写
np.random.rand(d0, d1, ..., dn):生成一个[0,1)之间的随机浮点数或N维浮点数组。
#生成2行3列的随机数数组,值在[0,1)之间
np.random.rand(2, 3)
np.random.randint(low, high=None, size=None, dtype='l'):生成一个整数或N维整数数组,取数范围:若high不为None时,取[low,high)之间随机整数,否则取值[0,low)之间随机整数。
C.从文本文件构造数组
arr2=np.loadtxt('2.txt')
将数组写入文本文件
np.savetxt('1.txt', arr1, fmt='%0.4f', delimiter=',')
delimiter: 数据的分隔符号,默认是空格;fmt:数据的保存格式,默认为'%.18e'
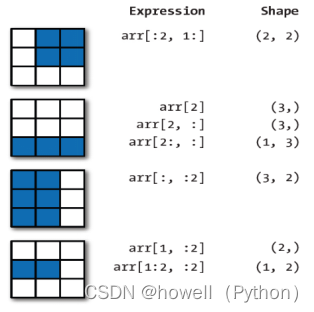
print(x[4:8])
arr = np.arange(10)
arr_slice = arr[5:8] #获得一个视图而不是新的数组
想通过切片获得新数组的方法: arr_slice = arr[5:8].copy()
print(arr2d[arr2d<0]) #用布尔型数组来索引
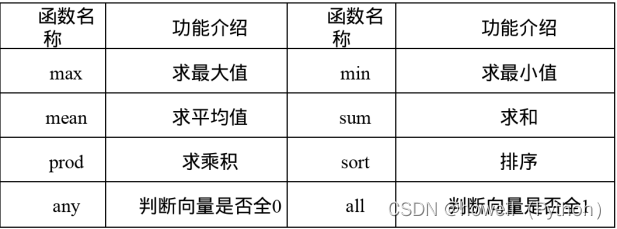
- 线性回归
导入库
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LinearRegression
from sklearn.metrics import mean_squared_error
from sklearn.metrics import r2_score
从文件中读取数据:
df=pd.read_csv(filename) 分别取出自变量和因变量
拆分训练集和测试集
x_train, x_test, y_train, y_test = train_test_split(x, y, test_size=0.25, random_state=33)
创建线性回归模型对象
lr = LinearRegression(normalize=True)
训练模型
lr.fit(x_train, y_train)
方程系数
print('回归方程的系数:',lr.coef_)
print('回归方程的截距:',lr.intercept_)
归一化
1)把数据变成(0,1)之间的小数。把数据映射到0~1范围之内处理,更加便捷快速。2)把有量纲表达式变成无量纲表达式,便于不同单位或量级的指标能够进行比较和加权。
def normalization(data):
_range = np.max(data,axis=0) - np.min(data,axis=0)
return (data - np.min(data,axis=0)) / _range
标准化
在机器学习中,我们可能要处理不同种类的资料,例如,音讯和图片上的像素值,这些资料可能是高维度的,资料标准化后会使每个特征中的数值平均变为0、标准差变为1。
def standard(data):
_mean=np.mean(data,axis=0)
_std=np.std(data,axis=0)
return (data - _mean) / _std
模型测试和拟合效果:均方误差
y_pred=lr.predict(x_test)
print(mean_squared_error(y_test,y_pred))
print('r2:',r2_score(y_test,y_pred))
可视化
x = df[['TV']]
y = df['sales']
x_train, x_test, y_train, y_test = train_test_split(x, y, test_size=0.25, random_state=33)
lr = LinearRegression()
lr.fit(x_train, y_train)
print('回归方程的系数:',lr.coef_)
print('回归方程的截距:',lr.intercept_)
y_pred=lr.predict(x_test)
print('MSE:',mean_squared_error(y_test,y_pred))
plt.plot(x_test,y_test,’b*’)
plt.plot(x_test,y_pred,color='blue',linewidth=3) #画出回归直线
- 逻辑回归
导入库
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LogisticRegression
import pandas as pd
从文件中读取数据:
data=pd.read_excel('test_pass.xlsx')
拆分训练集和测试集
col_names=['duration','efficiency','pass']
X_train,X_test,y_train,y_test=train_test_split(data[col_names[0:2]],data[col_names[2]],test_size=0.25,random_state=30)
创建线性回归模型对象
reg = LogisticRegression()
训练模型
reg.fit(X_train, y_train)
模型效果
score = reg.score(X_test, y_test)
#给定测试数据与实际标签相匹配的平均准确率
预测
learning =pd.DataFrame([[8, 0.9],[2, 0.6]])
result = reg.predict(learning)
可视化
plt.scatter(learning.iloc[:,0],learning.iloc[:,1],marker='^',c=result)
import numpy as npdef f(x):
y=x**3-x-1
return y
n=0
for i in np.arange(x,10,h):
if abs(f(i))<err:
print('root=','%.4f'%i,'\n','迭代次数:',n,sep='')
break
elif f(i)>0 and abs(f(i))>err:
print ('root=False','\n','迭代次数:',n,sep='')
break
else:
n+=1
例1:求x2-2=0的根,即求2的平方根
def f(x): return x**2-2
left=1;right=2;n=0#n用来统计二分次数
err=1e-6#误差
while True:
n+=1; middle=(left+right)*0.5
if abs(f(middle))<err:
print('f(x)=%.8f x=%.8f n=%d'%(f(middle),middle,n))
break
if f(middle)*f(left)>0: left=middle #中点变为左边界
else: right=middle #中点变为右边界
def f(x):
return x ** 2 -2
def df(x):
return x * 2
x=4;err=1e-6;n=0
while True:
if abs(f(x))<err:
print('fx=%.8f x=%.8f n=%d'%(f(x),x,n))
break
x=x-f(x)/df(x) #
n+=1
x0=1;x1=2;err=1e-6;n=0
def f(x):
return x**2-2
while True:
if f(x1)-f(x0)==0:
print('False')
break
x=x1-f(x1)/(f(x1)-f(x0))*(x1-x0)
n+=1
if abs(f(x))<err:
print('fx=%.8f x=%.8f n=%d'%(f(x),x,n))
break
x0=x1
x1=x
import numpy as np
np.random.seed(3)
x=np.random.randn(1);learning_rate=0.1
err=0.000001;max_iters=10000
def f(x): return x**2-10*x-30
def df(x): return 2*x-10
for i in range(max_iters):
print("第 %d 次迭代:x=%.8f y=%.8f"%(i,x,f(x)))
if abs(df(x)) <err: break
x=x-df(x) * learning_rate# xk+1=xk- η* f’(xk) (迭代公式)
import numpy as np
x=-1;y=-1
learning_rate=0.1
err=0.000001;max_iters=10000
def f(x,y):
return -np.exp(x-y)*(x**2-2*y**2)
def dx(x,y):
return -(np.exp(x-y)*(2*x)+(x**2-2*y**2)*np.exp(x-y))
def dy(x,y):
return -(np.exp(x-y)*(-4*y)+(x**2-2*y**2)*np.exp(x-y)*(-1))
for t in range(max_iters):
if t%100==0:
print("Iter %d, x=%.8f,y=%.8f,z=%.8f,dx=%.8f,dy=%.8f"%(t,x,y,f(x,y),dx(x,y),dy(x,y)))
if abs(dx(x,y))<err and abs(dy(x,y))<err:
print("Iter %d, x=%.8f,y=%.8f,z=%.8f,dx=%.8f,dy=%.8f"%(t,x,y,f(x,y),dx(x,y),dy(x,y)))
break
x=x-learning_rate*dx(x,y); y=y-learning_rate*dy(x,y) #迭代公式‘
import numpy as np
import matplotlib.pyplot as plt
#生成100个数据点
np.random.seed(3)
X=2*np.random.rand(100)#生成100个随机数,模拟x
Y=15+3*X+np.random.randn(100)#生成100个随机数,模拟y,真实的a=3,b=15
learning_rate=0.1; roundN = 5#对数据点集的轮数
np.random.seed(3); a=np.random.randn()
np.random.seed(4) ;b=np.random.randn()
def errorCompute(a,b):
error=0
for j in range(len(X)):
error+=1/2*(a*X[j]+b-Y[j])**2
return error/len(X)
for i in range(roundN):
for j in range(len(X)):
if j%50==0:
print("round=%d,iter=%d,a=%f,b=%f,E=%f"%(i,j,a,b,errorCompute(a,b)))
gradA=(a*X[j]+b-Y[j])*X[j]; gradB=a*X[j]+b-Y[j] #求偏导的公式
a=a-learning_rate*gradA; b=b-learning_rate*gradB #迭代公式
#下面绘制图形
maxX=max(X); minX=min(X); maxY=max(Y); minY=min(Y)
X_fit=np.arange(minX,maxX,0.01); Y_fit=a*X_fit+b
plt.plot(X,Y,‘.’)#数据点
plt.plot(X_fit,Y_fit,'r-',label='Gradient Descent')
plt.plot(X_fit,15+3*X_fit,'b-',label='True')
plt.legend()
plt.show()
import numpy as np
from sklearn.model_selection import train_test_split
#数据处理
data=np.loadtxt('advertising.txt',delimiter=',')
X=data[:,0:-1]
y=data[:,-1]
X=(X-X.min(axis=0))/(X.max(axis=0)-X.min(axis=0))
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.25, random_state=42)
#梯度下降法,y=w1*x1+w2*x2+w3*x3+b
#初始化
np.random.seed(10)
w1,w2,w3,w4,b=np.random.randn(5)
lr=0.001# 0.00001
rounds=1000 #300,0.001 ,4.54
def computeErr(X,y): #误差计算
err=0
for i in range(len(X)):
err+=1/2*(X[i,0]*w1+X[i,1]*w2+X[i,2]*w3+b-y[i])**2
return err/len(X)
for i in range(rounds): #梯度下降法拟合训练集
for j in range(len(X_train)):
w1-=lr*(X_train[j,0]*w1+X_train[j,1]*w2+X_train[j,2]*w3+b-y_train[j])*X_train[j,0]
w2-=lr*(X_train[j,0]*w1+X_train[j,1]*w2+X_train[j,2]*w3+b-y_train[j])*X_train[j,1]
w3-=lr*(X_train[j,0]*w1+X_train[j,1]*w2+X_train[j,2]*w3+b-y_train[j])*X_train[j,2]
b-=lr*(X_train[j,0]*w1+X_train[j,1]*w2+X_train[j,2]*w3+b-y_train[j])
if i%100==0:
print('第%i轮迭代训练集误差=%.2f'%(i,computeErr(X_train,y_train)))
#模型评估
print('测试集误差:',computeErr(X_test,y_test))
print('权重:',w1,w2,w3)
print('截距:',b)
predict=(X_test*np.array([w1,w2,w3])).sum(axis=1)+b
mse=((predict-y_test)**2).sum()/len(y_test)
print('rmse=',mse**0.5)


