K-SVD字典学习算法_k-svd算法来学习字典

1.提出问题：什么是稀疏表示
假设我们用一个MN的矩阵表示数据集Y，每一行代表一个样本，每一列代表样本的一个属性，一般而言，该矩阵是稠密的，即大多数元素不为0。
稀疏表示的含义是，寻找一个系数矩阵X（KN）以及一个字典矩阵D（MK），使得DX尽可能的还原Y，且X尽可能的稀疏。X便是Y的稀疏表示。

算法思想

算法求解思路为交替迭代的进行稀疏编码和字典更新两个步骤. K-SVD在构建字典步骤中，K-SVD不仅仅将原子依次更新，对于原子对应的稀疏矩阵中行向量也依次进行了修正. 不像MOP，K-SVD不需要对矩阵求逆，而是利用SVD数学分析方法得到了一个新的原子和修正的系数向量.

$固定系数矩阵X和字典矩阵D，字典的第k个原子为d_k，同时d_k对应的稀$
$疏矩阵为X中的第k个行向量x_T^k.假设当前更新进行到原子d_k，样本矩阵和$字典逼近的误差为：

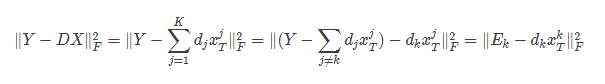
$在得到当前误差矩阵E_k后，需要调整d_k和X_T^k，使其乘积与E_k的误差尽可能的小.$
$如果直接对d_k和X_T^k进行更新，可能导致x_T^k不稀疏.所以可以先把原有向量x_T^k中零$
$元素去除，保留非零项，构成向量x_R^k，然后从误差矩阵E_k中取出相应的列向量，$
$构成矩阵E_k^R.对E_k^R进行SVD（SingularValueDecomposition）分解，有E_k^R=$
$U\Delta V^T，由U的第一列更新d_k，由V的第一列乘以\Delta (1,1)所得结果更新x_R^k.$

代码

import numpy as np
import matplotlib.pyplot as plt
from numpy import *
import scipy.io as sio
import random
from sklearn import linear_model
import scipy.misc
from PIL import Image
def esErrDic(data,recons):
    m,n=data.shape
    esErr=0
    for i in range(m):
        for j in range(n):
            esErr+=(data[i][j]-recons[i][j])**2
    return esErr/(m*n) 
class KSVD(object):
    def __init__(self, n_components, max_iter=100, tol=1e-6,n_nonzero_coefs=None):
        """
        稀疏模型Y = DX，Y为样本矩阵，使用KSVD动态更新字典矩阵D和稀疏矩阵X
        :param n_components: 字典所含原子个数（字典的列数）
        :param max_iter: 最大迭代次数
        :param tol: 稀疏表示结果的容差
        :param n_nonzero_coefs: 稀疏度
        """
        self.dictionary = None
        self.sparsecode = None 
        self.max_iter = max_iter 
        self.tol = tol 
        self.n_components = n_components 
        self.n_nonzero_coefs = n_nonzero_coefs
    def _initialize(self, y):
        """
        初始化字典矩阵
        """
        u, s, v = np.linalg.svd(y)
        self.dictionary = u[:, :self.n_components]
    def _update_dict(self, y, d, x):
        """
        使用KSVD更新字典的过程
        """
        for i in range(self.n_components):
            index = np.nonzero(x[i, :])[0]#选出Xk中非零的元素下标
            if len(index) == 0:
                continue
            d[:, i] = 0
            r = (y - np.dot(d, x))[:, index] 
            u, s, v = np.linalg.svd(r, full_matrices=False) 
            d[:, i] = u[:, 0].T 
            x[i, index] = s[0] * v[0, :]
        return d, x
    def fit(self, y):
        """
        KSVD迭代过程
        """
        self._initialize(y)
        for i in range(self.max_iter):
            x = linear_model.orthogonal_mp(self.dictionary, y, n_nonzero_coefs=self.n_nonzero_coefs)
            e = np.linalg.norm(y - np.dot(self.dictionary, x)) 
            if e < self.tol:
                break
            self._update_dict(y, self.dictionary, x)
        self.sparsecode = linear_model.orthogonal_mp(self.dictionary, y, n_nonzero_coefs=self.n_nonzero_coefs) 
        return self.dictionary, self.sparsecode
if __name__ == '__main__':
    file='G:/lecture of grade one/pattern recognition/trial_two/train_data2_807802844.mat'
    Img=loadData(file)
    #字典学习部分代码，其中KSVD的参数就是原子个数，可修改
    ksvd = KSVD(100)
    dictionary, sparsecode = ksvd.fit(Img['Data'])
    recons=dictionary.dot(sparsecode)
    err=esErrDic(Img['Data'],recons)
	'''
    #测试KSVD代码的调试代码，选择一张图片，用自己编写的KSVD对其进行字典学习
    image =Image.open('/home/swh/Downloads/scene.jpeg')
    image = np.array(image)
    image=image[:,:,0]
    im_ascent = image.astype('float32')
    #im_ascent = scipy.misc.ascent().astype(np.float)
    ksvd = KSVD(30) 
    dictionary, sparsecode = ksvd.fit(im_ascent) 
    plt.figure() 
    plt.subplot(1, 2, 1) 
    plt.imshow(im_ascent) 
    plt.subplot(1, 2, 2) 
    recon=dictionary.dot(sparsecode)
    plt.imshow(recon) 
    plt.show()
    '''
        
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89