数据结构——链表专题3

一、判断链表是否有环

原题链接：判断链表是否有环

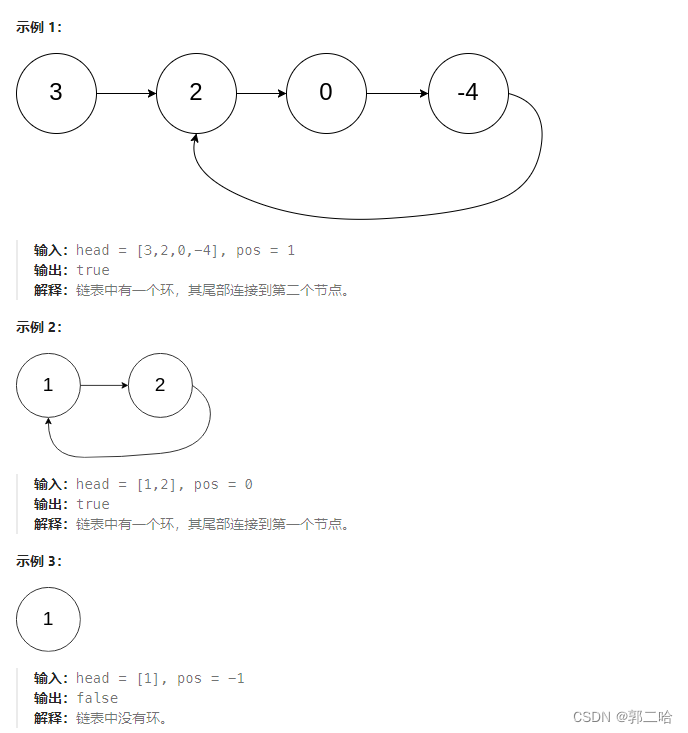
这道题可以使用快慢指针，fast一次走两步，slow一次走一步，如果有环，它们在环里面必定会相遇

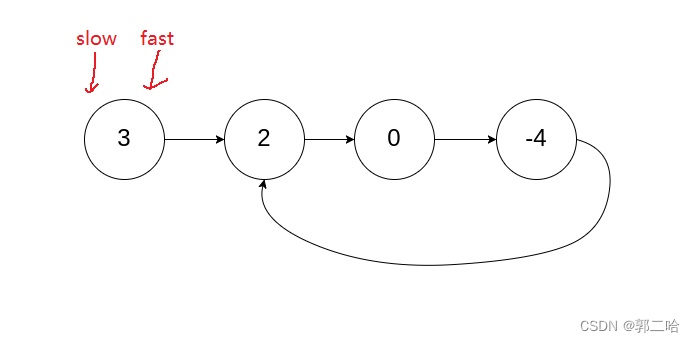
bool hasCycle(struct ListNode *head)
{
    if(head == NULL)
    {
        return head;
    }
    struct ListNode* slow = head;
    struct ListNode* fast = head;
    while(fast && fast->next)
    {
        fast = fast->next->next;
        slow = slow->next;
        if(fast == slow)
        {
            return true;
        }
    }
    return false;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19

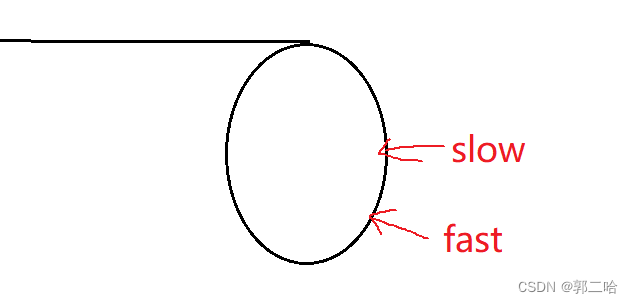
那么为什么一定会相遇呢？

对于快指针一次走两步来说，在slow进环后，假设slow与fast的距离为N

很明显，快指针走两步时，慢指针走一步，在进环后它们之间的差距为1，所以它们一定会相遇

那么快指针走三步？四步？五步呢？现在让我们证明一下：
现在我们规定快指针走三步，那么在进环后它们之间的差距为2

如果N是偶数那么在slow进环后一圈之内就能遇见fast
如果N是奇数那么在slow进环后一圈之内不能遇见fast,fast会超越slow一步，那么就不能相遇了吗？

假设在slow进环前，走过的距离是L,环的长度为C，fast在环内走过的距离为XC,slow进环时，slow与fast之间的距离为N

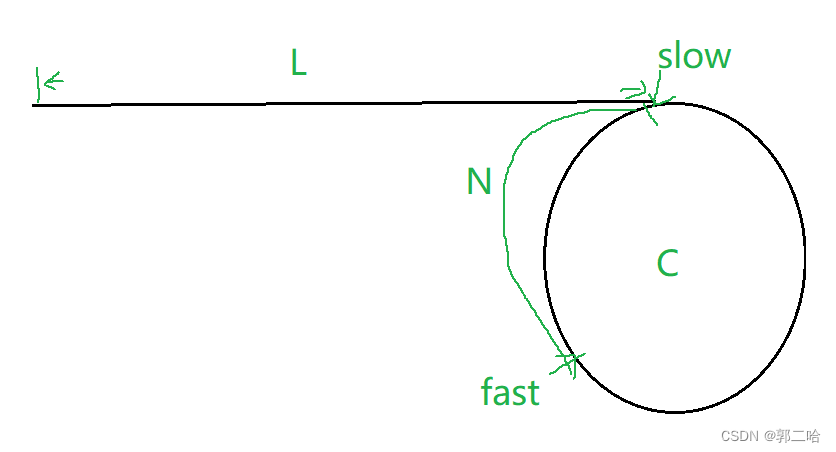
现在我们分析N是奇数的情况：

很好，现在我们只需要分析N为奇数时，C为偶数的情况是否存在？

结论：一定能追上
当N是偶数时，一轮就能追上
当N是奇数时，第一轮追不上，第二轮能追上

二、返回入环的第一个节点

原题链接：返回入环的第一个节点

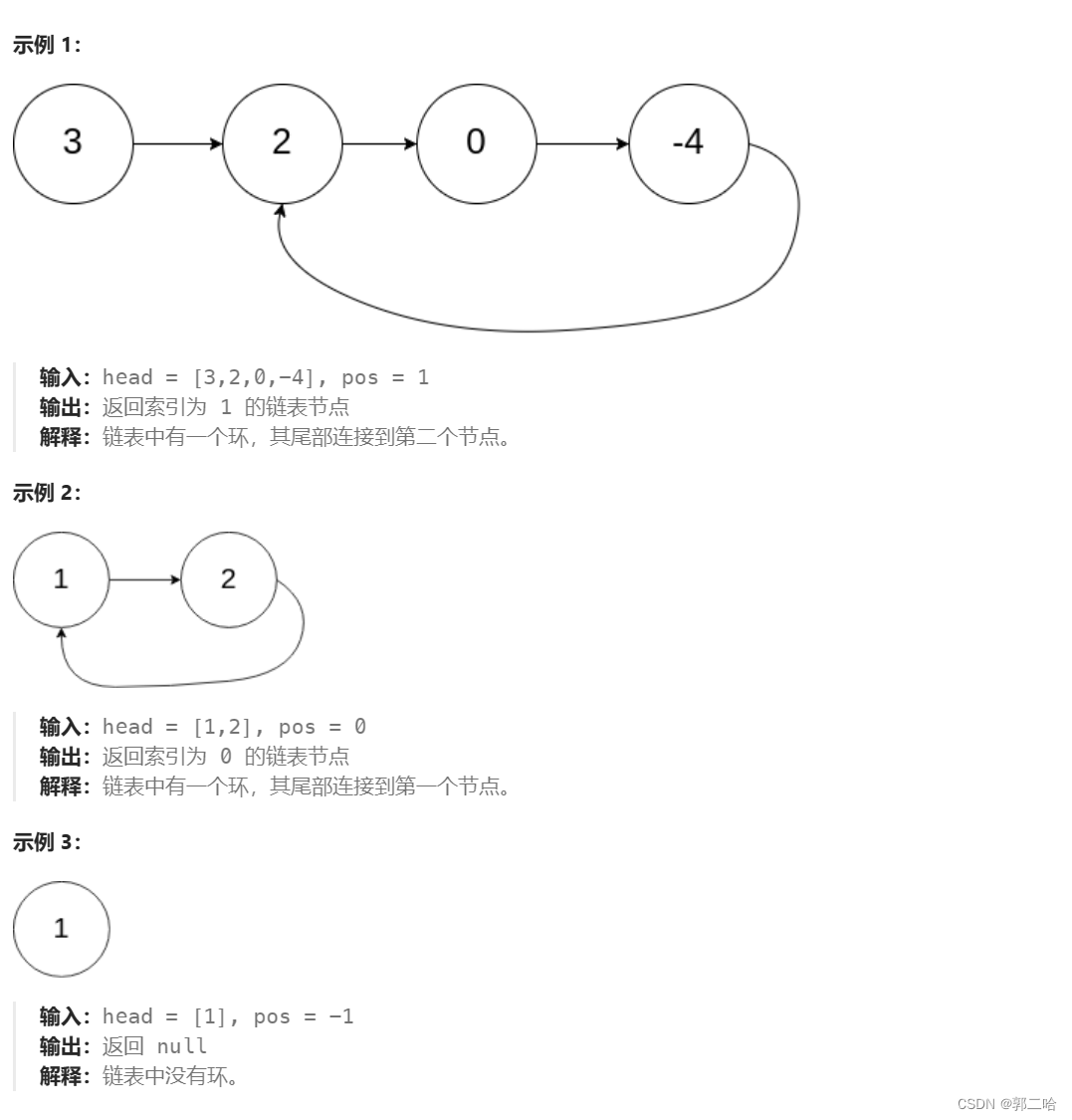
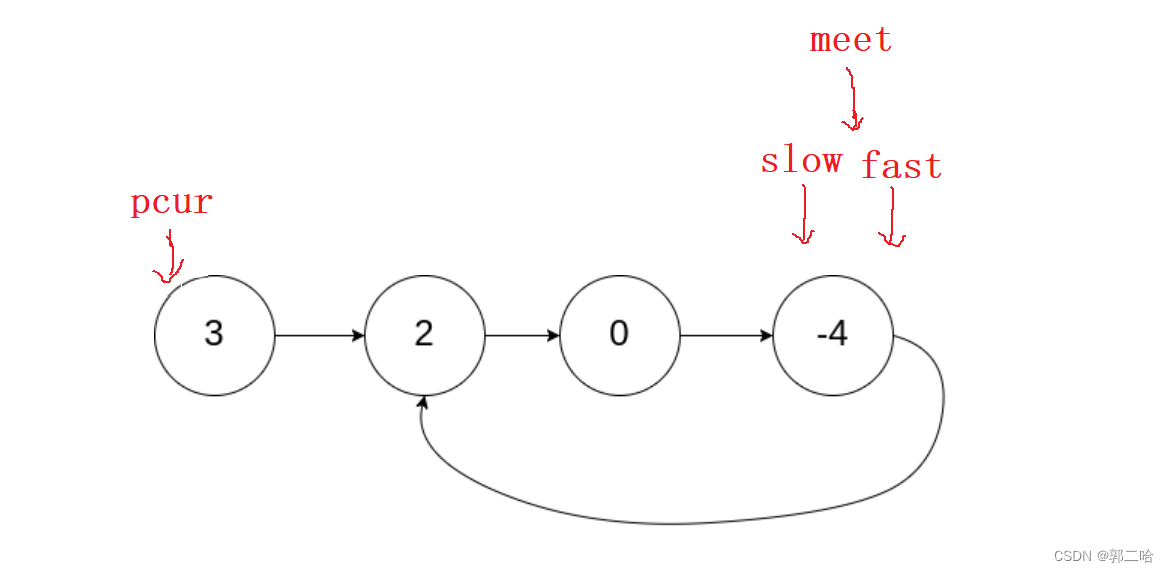
思路：先使用快慢遍历链表，用meet指针指向它们相遇的结点，然后用pcur指针指向链表的头结点
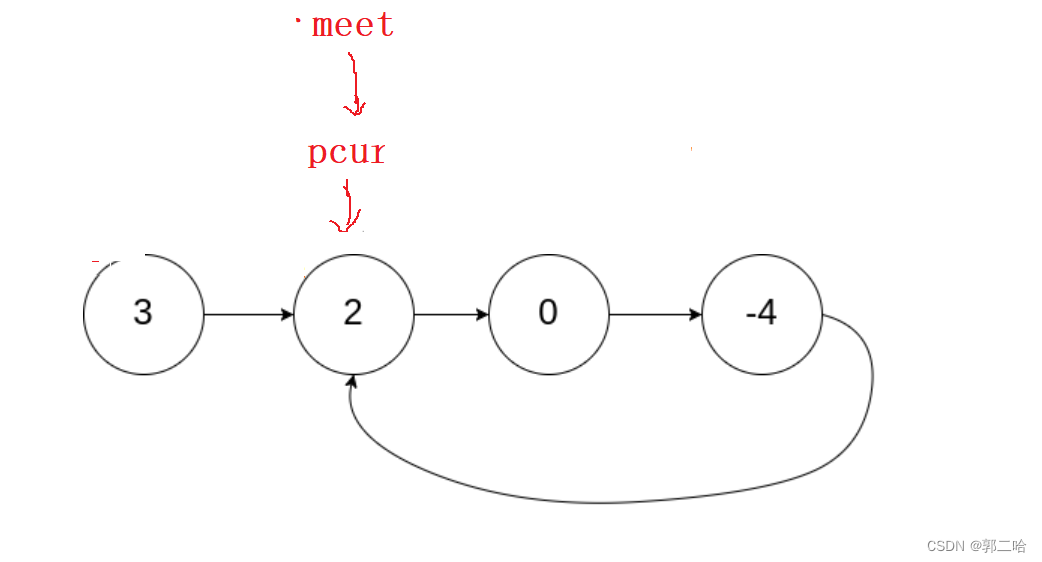
最后让pcur和meet指针同时移动，每次移动一步，最终它们会在环的头结点相遇

struct ListNode *detectCycle(struct ListNode *head)
{
    if(head == NULL)
    {
        return head;
    }
    struct ListNode* fast = head;
    struct ListNode* slow = head;
    while(fast && fast->next)
    {
        fast = fast->next->next;
        slow = slow->next;
        if(fast == slow)
        {
            struct ListNode* meet = slow;
            struct ListNode* pcur = head;
            while(meet != pcur)
            {
                meet = meet->next;
                pcur = pcur->next;
            }
            return meet;
        }
    }
    return NULL;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26

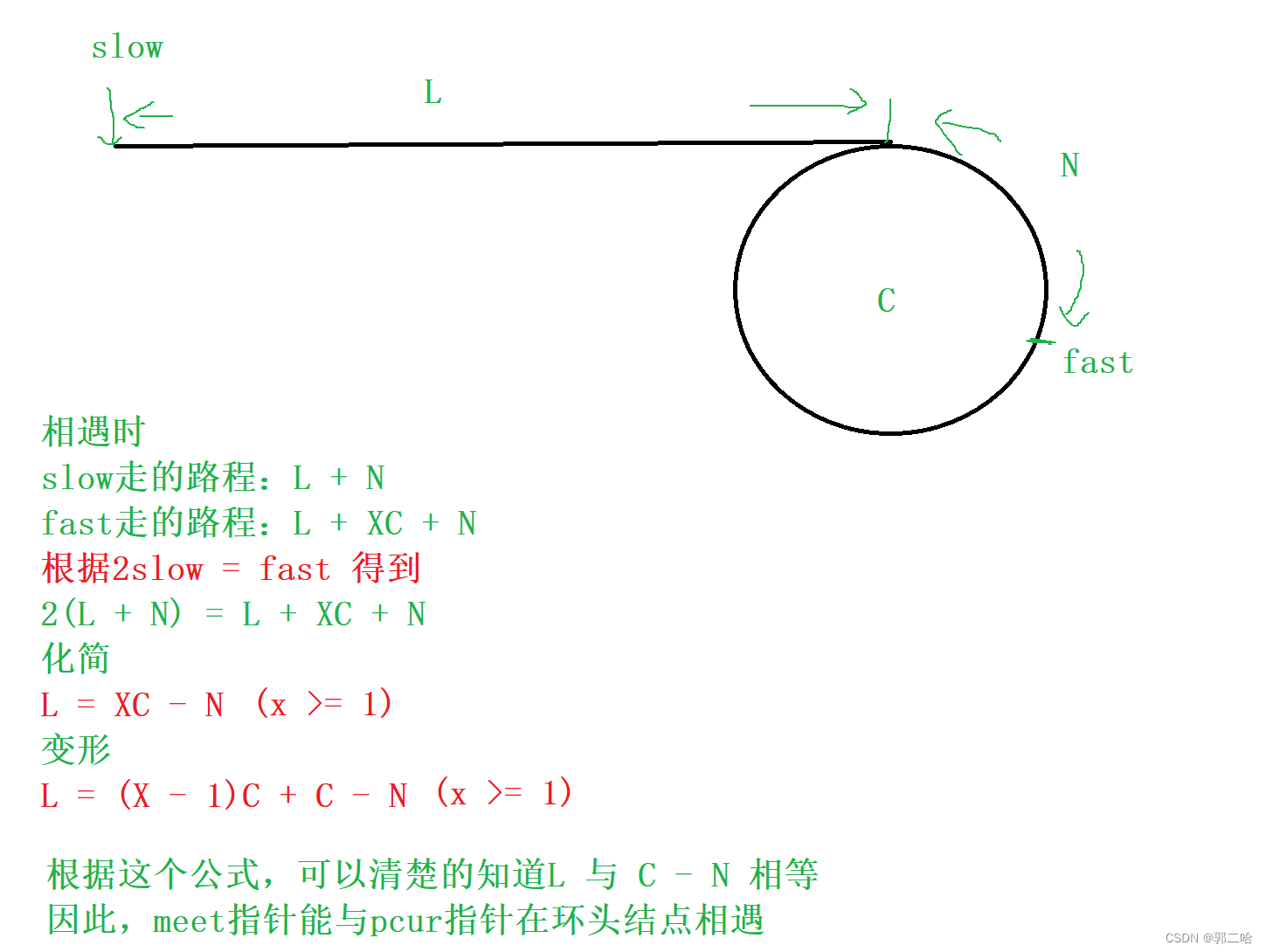
证明：为什么meet指针一定与pcur指针在环头结点相遇？

假设在slow进环前，走过的距离是L,环的长度为C，fast在环内走过的距离为XC,
在slow位于链表的头结点时，fast与环的头结点之间的距离为N

三、随机链表的复制

原题链接：随机链表的复制

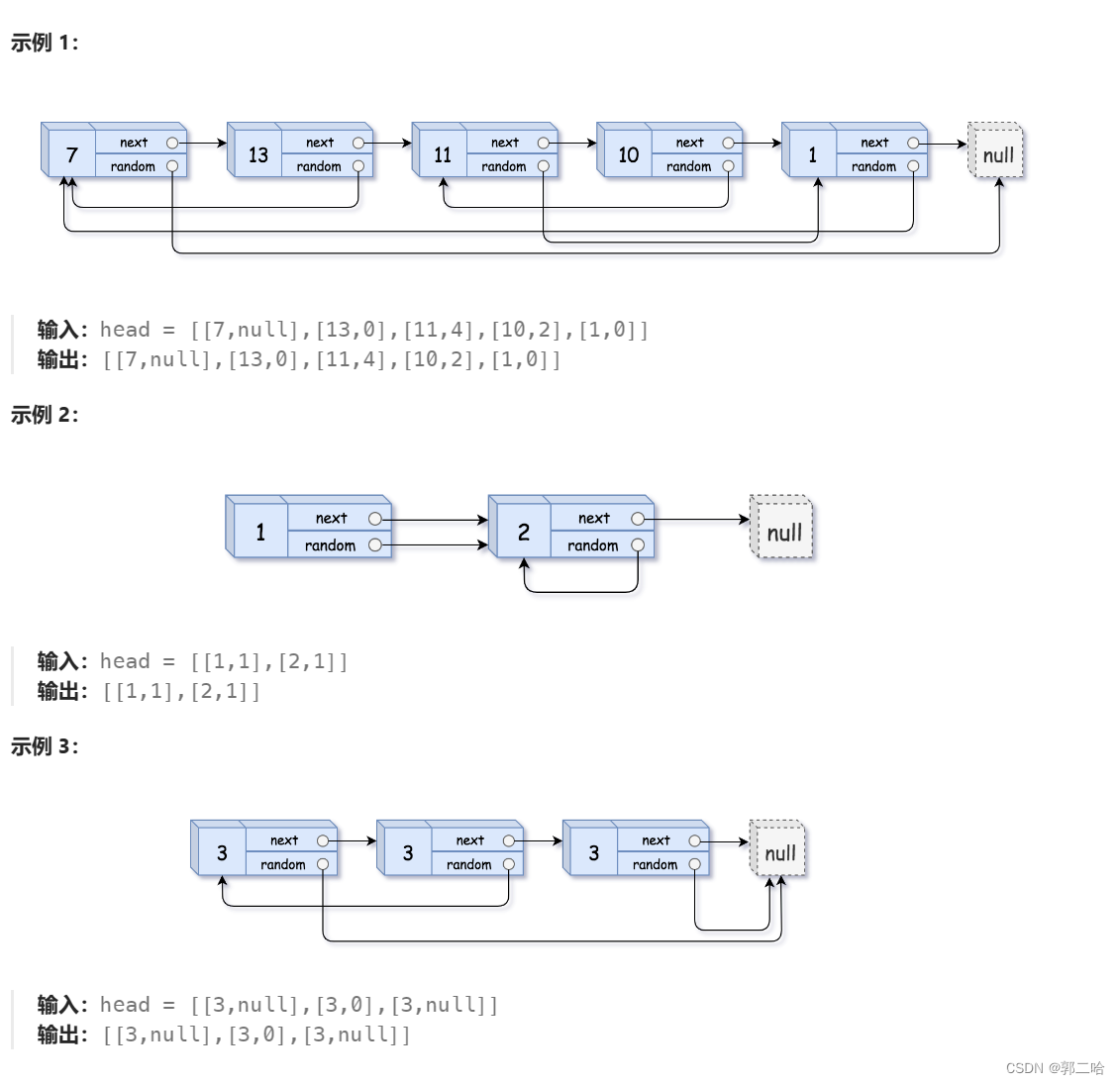
思路：
在原链表的基础上，在每个结点后面创建一个新结点，这个新结点保存着前面结点的数据
然后将新结点的random指针指向对应的位置
最后将新的结点从原链表上面脱离（此过程中可以选择恢复原链表），形成新的链表

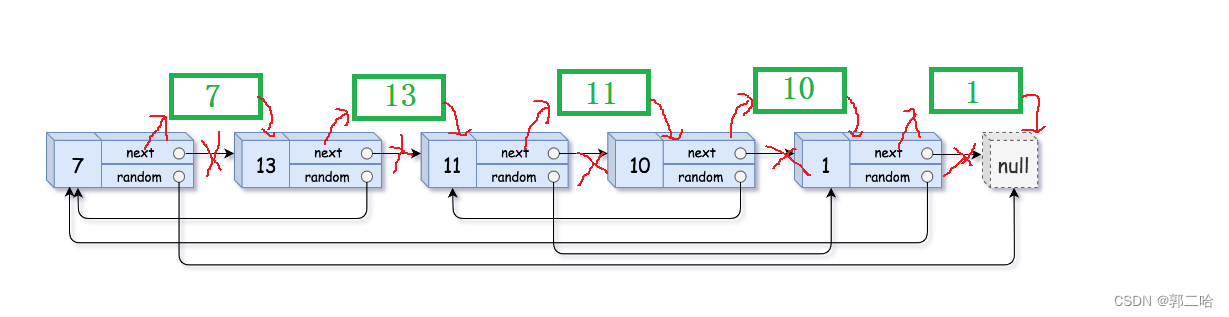
struct Node* copyRandomList(struct Node* head)
{
    //拷贝原结点
	struct Node* pcur = head;
    while(pcur)
    {
        struct Node* copy = (struct Node*)malloc(sizeof(struct Node));
        if(copy == NULL)
        {
            exit(1);
        }
        copy->val = pcur->val;
        copy->next = pcur->next;
        pcur->next = copy;
        pcur = copy->next;
    }
    //拷贝random指针
    pcur = head;
    while(pcur)
    {
        struct Node* copy = pcur->next;
        if(pcur->random == NULL)
        {
            copy->random = NULL;
        }
        else
        {
            copy->random = pcur->random->next;
        }
        pcur = copy->next;
    }
    //脱离原链表
    pcur = head;
    struct Node* phead = NULL;
    struct Node* ptail = NULL;
    while(pcur)
    {
        struct Node* copy = pcur->next;
        struct Node* next = copy->next;
        if(phead == NULL)
        {
            phead = ptail = copy;
        }
        else
        {
            ptail->next = copy;
            ptail = ptail->next;
        }
        //恢复原链表
        pcur->next = next;
        pcur = next;
    }
    return phead;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54