devbox
Monodyee
这个屌丝很懒，什么也没留下！
关注作者
热门标签
热门文章
当前位置:   article > 正文

AI生成中Transformer模型_位置前馈网络

作者：Monodyee | 2024-06-09 10:35:00

赞

踩

位置前馈网络

介绍

在深度学习中，有很多需要处理时序数据的任务，比如语音识别、文本理解、机器翻译、音乐生成等。

Transformer模型由Vaswani等人在2017年的论文《Attention Is All You Need》中首次提出，它在自然语言处理领域引起了巨大变革。该模型摒弃了传统的循环网络结构，转而使用自注意力机制，允许模型同时处理输入序列的各个部分，从而更有效地捕捉复杂的语言模式。Transformer架构包含编码器和解码器两部分，每部分由多个包含多头自注意力和位置感知前馈网络的相同层组成。

https://arxiv.org/pdf/1706.03762.pdf

应用于许多领域

  • 机器翻译：Transformer在提供快速、准确翻译方面表现出色。
  • 文本生成：如GPT系列模型，在自动内容创作、对话生成等方面具有显著效果。
  • 文本理解：如BERT模型，用于情感分析、文本分类、问答系统等。
  • 语音处理：Transformer被用于语音识别和语音合成。
  • 图像处理：虽然最初是为NLP设计的，但Transformer也已被适配用于图像分类和生成任务。
  • 生物信息学：用于蛋白质结构预测等复杂任务。
  • 视频处理：用于视频理解和视频生成任务。

历史

Transformer模型作为继多层感知器（MLP）、卷积神经网络（CNN）和递归神经网络（RNN）之后的第四种主要深度学习架构，代表了自然语言处理技术的重大进步。

MLP是早期的神经网络模型，主要用于简单模式识别。

随后，CNN的出现改进了图像处理和计算机视觉领域。

RNN和LSTM在处理时序数据和语言模型方面取得了显著成果。
然而，RNN在处理长序列时存在梯度消失问题。Transformer通过自注意力机制，有效地解决了长距离依赖问题，极大提高了模型处理序列数据的能力，尤其是在NLP领域。

CNN 和 Transformer 区别

CNN（卷积神经网络）擅长处理具有空间关系的数据，如图像，因其能有效提取和学习空间特征。

相比之下，Transformer模型通过自注意力机制，更擅长处理序列数据，如文本，因其能有效捕捉长距离依赖关系。

CNN在图像识别、物体检测等领域表现突出，而Transformer则在自然语言处理和序列到序列的任务（如机器翻译）中表现卓越。

两者各有专长，应用于不同类型的问题和数据。

数学公式

CNN（卷积神经网络）的核心数学公式涉及卷积操作。在卷积层中，输入图像 ( I ) 与卷积核 ( K ) 通过卷积操作生成特征图 ( F )。卷积操作可以表示为：

F ( i , j ) = ∑ m ∑ n I ( i − m , j − n ) K ( m , n ) F(i, j) = \sum_m \sum_n I(i - m, j - n) K(m, n) F(i,j)=m∑​n∑​I(i−m,j−n)K(m,n)

其中，( m ) 和 ( n ) 是卷积核的尺寸，( i ) 和 ( j ) 是输出特征图的位置。此外，CNN还经常使用池化层和激活函数，如 ReLU ( ReLU ( x ) = max ⁡ ( 0 , x ) ) ( \text{ReLU}(x) = \max(0, x) ) (ReLU(x)=max(0,x))，来进一步处理特征图。

RNN 和 LSTM 解决序列问题

RNN

https://ieeexplore.ieee.org/document/6795228

RNN（递归神经网络）是专门用于处理序列数据的架构。其优点包括能够处理任意长度的序列、适用于时序数据分析（如语音识别、语言建模）。

RNN的主要缺点是梯度消失或爆炸问题，这使得训练长序列变得困难。

此外，RNN不能并行处理序列的各个部分，导致计算效率较低。尽管LSTM和GRU等变体有所改进，但它们仍受限于处理长距离依赖的能力。

CNN 需要固定长度的输入、输出，RNN 的输入和输出可以是不定长且不等长的
CNN 只有 one-to-one 一种结构，而 RNN 有多种结构，如下图：
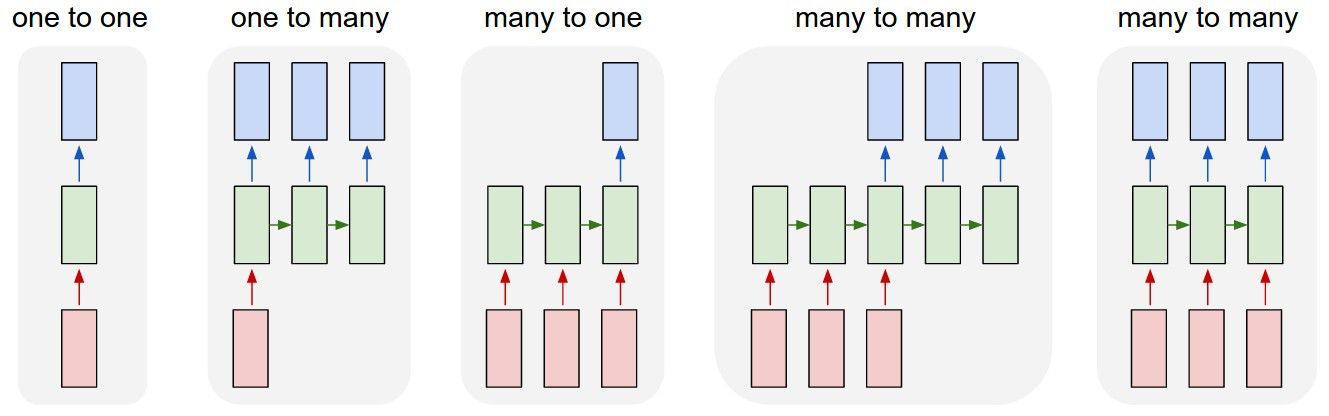
https://www.jiqizhixin.com/articles/2018-12-14-4

RNN 数学公式

在RNN（递归神经网络）中，最基础的数学公式是用来计算隐状态的。对于时间步 ( t )，RNN的隐状态 ( h t ) ( h_t ) (ht​) 通常通过以下公式计算：

h t = f ( W ⋅ h t − 1 + U ⋅ x t + b ) h_t = f(W \cdot h_{t-1} + U \cdot x_t + b) ht​=f(W⋅ht−1​+U⋅xt​+b)

这里，h_{t-1} 是前一时间步的隐状态，( x_t ) 是当前时间步的输入，( W ) 和 ( U ) 是权重矩阵，( b ) 是偏置项，而 ( f ) 是激活函数，常用的是tanh或ReLU。每个时间步都会更新隐状态，隐状态在序列中传递信息。

LSTM

http://colah.github.io/posts/2015-08-Understanding-LSTMs/

  • LSTM是一种特殊的RNN,可以学习长期依赖关系。其关键创新点是cell
    state,它可以跨时间步传递信息,避免了普通RNN中的梯度消失和爆炸问题。

  • LSTM由一个循环模块组成,每个模块包含输入门、遗忘门、输出门以及一个候选cell状态。门控结构可以控制信息的流动。

  • 输入门控制新信息进入cell state的程度。遗忘门控制旧信息被遗忘的程度。输出门控制输出的内容。候选cell状态生成新的候选状态值。

  • 经过这四个门的处理,LSTM可以遗忘不重要的旧信息,只保留重要的信息,同时避免不相关的新信息进入cell
    state,有效地建模长期依赖关系。

  • LSTM有多种变体,如添加peephole连接、使用耦合的输入遗忘门、GRU等,但基本思想都是使用门控结构来控制cell state。

  • LSTM已在NLP、语音识别、机器翻译等任务上取得了非常好的效果。可以说LSTM是使RNN实现长期依赖成为可能的关键创新点。

Transformer vs LSTM

Transformer和LSTM都用于自然语言处理，但各有所长。Transformer以自注意力机制著称，擅长并行处理和处理长距离依赖，适合用于翻译和文本生成等任务。

LSTM作为一种RNN，擅长捕捉序列信息和上下文，适用于时间序列分析和语音识别。

然而，它在处理长序列时会遇到梯度消失问题，这是Transformer所解决的问题。

在多种自然语言处理任务中，Transformer的性能已经大大超过了LSTM。

Encoder-Decoder 架构

在这里插入图片描述

Encoder-Decoder架构是一种在深度学习中常用的模型结构，特别是在处理如机器翻译、文本摘要等序列到序列（seq2seq）的任务时。

这种架构包括两部分：编码器（Encoder）和解码器（Decoder）。

编码器处理输入数据（如文本序列），将其转换为一个固定大小的内部表示（context vector），这个表示捕捉了输入数据的关键信息。

解码器使用这个内部表示来生成输出数据（如另一种语言的文本）。这种架构允许模型有效地处理输入和输出序列之间的复杂关系，尤其适用于输入和输出长度不匹配的情况。

注意力机制

注意力机制(Attention Mechanism)是机器学习中比较重要的一个突破,主要用来改善神经网络对长序列进行建模的能力。

  • 2014年,Bahdanau等人在机器翻译任务中首次引入注意力机制,可以自动搜索源句子中对当前翻译目标词相关的源词,实现可解释的神经机器翻译,大幅提高了翻译质量。

  • 2015年,Rush等人将注意力机制引入自然语言处理中的问答任务中,可以关注与问题及答案相关的词语,提高了问答的准确率。

  • 2016年,Vaswani等人在Transformer模型中只使用注意力机制而完全抛弃RNN/CNN,取得了当时最好的机器翻译结果。这表明仅用注意力就能达到非常强大的建模能力。

  • 2017年,Veličković等人提出图注意力网络(GAT),将注意力机制引入到图神经网络中,达到了当时最好的节点分类效果。

  • 2018年,Devlin等人提出BERT模型,通过双向Masked语言模型及下一句预测任务 pretrain
    得到通用语言表示,然后可用于下游NLP任务,取得了当时最优的结果。

当前,注意力机制与Transformer等结合,已成为NLP领域的标准组件和主流方法。它也广泛应用在计算机视觉、语音识别等领域。

解决问题

注意力机制可以解决Encoder-Decoder架构的某些限制，特别是与长序列相关的问题。在标准的Encoder-Decoder模型中，编码器必须将所有输入信息压缩成一个固定大小的上下文向量，这可能导致信息丢失。

注意力机制允许解码器在生成每个输出元素时“关注”输入序列中的不同部分，从而有效地解决信息压缩的问题。

这样，解码器可以直接访问整个输入序列，从而更准确地生成输出。注意力机制的引入显著提高了诸如机器翻译、文本摘要等任务的性能。

数学公式

在注意力机制中，核心数学公式定义了输入和输出之间的注意力权重。对于一个给定的查询 ( Q )，键 ( K )，和值 ( V )，注意力权重通过下面的softmax函数计算得到：

Attention ( Q , K , V ) = softmax ( Q K T d k ) V \text{Attention}(Q, K, V) = \text{softmax}\left(\frac{QK^T}{\sqrt{d_k}}\right)V Attention(Q,K,V)=softmax(dk​ ​QKT​)V

这里， ( d k ) ( d_k ) (dk​) 是键的维度，这个缩放因子有助于训练稳定性。在多头注意力中，输入会被分割到多个头上，每个头计算它们自己的注意力分数，并行地进行，然后将这些头的输出拼接起来，最后通过一个线性层进行输出。这允许模型在不同的子空间中捕捉信息。

Transformer 的整体方案

https://arxiv.org/pdf/1706.03762.pdf

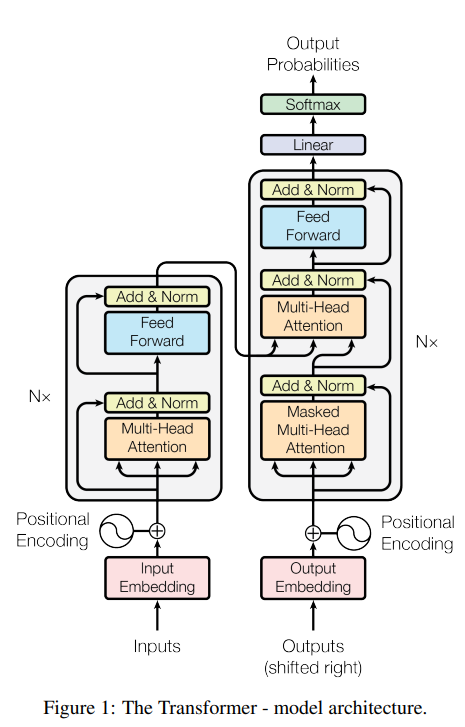
在这里插入图片描述
这张图展示的是Transformer模型的架构。

在这个架构中，输入首先经过嵌入层，并添加位置编码，以保持序列中的位置信息。

然后输入通过N个相同的编码层，每层都包含两个主要部分：多头注意力机制和前向传播网络。

多头注意力层帮助模型在编码时关注输入序列中的不同部分，而前向传播网络则进行非线性变换。

每个编码层的输出都会传递到下一个层。

在解码器侧，除了这两个组件外，还有一个额外的遮蔽多头注意力层，防止在预测下一个词时看到未来的信息。

最后，解码器的输出通过一个线性层和Softmax层来预测输出序列中每个元素的概率分布。

点乘注意力机制

在这里插入图片描述
展示了点乘注意力机制（Scaled Dot-Product Attention）的流程。

首先，查询（Q）、键（K）和值（V）通过矩阵乘法（MatMul）操作进行点积，然后通过缩放操作来调整大小。

接下来，可选择性地应用掩码操作，通常用于遮蔽序列中未来的信息以防止信息泄露。

然后通过SoftMax函数将其转换为注意力权重，最后这些权重应用到值（V）上，通过另一次矩阵乘法得到加权的输出，这个输出反映了模型对输入的不同部分的关注程度。

多头自注意力

多头自注意力（Multi-Head Self-Attention）是Transformer架构中的一种关键机制，它允许模型在处理序列数据时，同时关注序列中多个位置的信息。其数学表达通常包括以下几个步骤：

  1. 线性投影：输入序列的每个元素被映射到多组查询（Q）、键（K）和值（V）向量。

  2. 计算注意力分数：每个查询与所有键的点积被计算出来，以表示它们之间的关联强度。

  3. 缩放和归一化：点积通常被除以一个缩放因子（如 ( d k ) ( \sqrt{d_k} ) (dk​ ​)，其中 ( d k ) ( d_k ) (dk​) 是键向量的维度），然后应用softmax函数进行归一化，得到注意力权重。

  4. 应用注意力权重：得到的注意力权重被用于加权值（V）向量的聚合。

  5. 输出拼接：多头上的输出被拼接起来，并通过一个线性层进行整合。

其数学公式如下：

MultiHead ( Q , K , V ) = Concat ( head 1 , … , head h ) W O \text{MultiHead}(Q, K, V) = \text{Concat}(\text{head}_1, \ldots, \text{head}_h)W^O MultiHead(Q,K,V)=Concat(head1​,…,headh​)WO

其中每个头部 ( head i ) ( \text{head}_i ) (headi​) 计算为：

head i = Attention ( Q W i Q , K W i K , V W i V ) \text{head}_i = \text{Attention}(QW_i^Q, KW_i^K, VW_i^V) headi​=Attention(QWiQ​,KWiK​,VWiV​)

而Attention函数定义为：

Attention ( Q , K , V ) = softmax ( Q K T d k ) V \text{Attention}(Q, K, V) = \text{softmax}\left(\frac{QK^T}{\sqrt{d_k}}\right)V Attention(Q,K,V)=softmax(dk​ ​QKT​)V

在这里， ( W i Q ) ( W_i^Q ) (WiQ​), ( W i K ) ( W_i^K ) (WiK​), 和 ( W i V ) ( W_i^V ) (WiV​)
是投影矩阵， ( W O ) ( W^O ) (WO) 是用于拼接后的输出的线性层的权重矩阵。这个机制允许模型在不同的表示子空间中学习信息，并在整个序列中捕获复杂的依赖关系。

架构

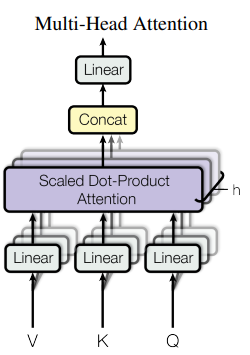
在这里插入图片描述

这个图展示的是多头自注意力（Multi-Head Attention）的组件部分。

输入的Q（查询），K（键）和V（值）首先经过线性变换，为每个头生成不同的表示。

然后，每个头进行缩放点积注意力操作，这个过程包括计算Q和K的点积，应用缩放因子，然后进行softmax归一化得到权重，最后这个权重应用于V。

所有头的输出被拼接在一起，再通过另一个线性变换生成最终的输出。这样，模型可以在不同的表示子空间中并行捕获信息。

位置前馈网络

Position-wise Feed Forward Networks（位置前馈网络）是Transformer架构中的一个重要组成部分。

在每个编码器和解码器层中，经过多头注意力机制处理的数据将被送入两层线性变换和一个激活函数的网络中。

这个网络在序列的每个位置独立地应用相同的操作，因此被称为“逐位置”。

通常，激活函数是ReLU或GELU。这种设计使得网络能够在保持序列信息的同时增加非线性，从而捕捉更复杂的数据特征。

位置前馈网络的数学公式涉及到两个线性变换和一个非线性激活函数。对于给定的输入 ( X )，逐位置前馈网络的计算可以表示为：

FFN ( X ) = max ⁡ ( 0 , X W 1 + b 1 ) W 2 + b 2 \text{FFN}(X) = \max(0, XW_1 + b_1)W_2 + b_2 FFN(X)=max(0,XW1​+b1​)W2​+b2​

这里， ( W 1 ) ( W_1 ) (W1​) 和 ( W 2 ) ( W_2 ) (W2​) 是权重矩阵， ( b 1 ) ( b_1 ) (b1​) 和 ( b 2 ) ( b_2 ) (b2​) 是偏置项，ReLU函数 ( max ⁡ ( 0 , ⋅ ) ) ( \max(0, \cdot) ) (max(0,⋅)) 用作激活函数。这个操作对输入 ( X ) ( X ) (X)的每个位置独立应用。

位置编码

在Transformer架构中,Positional Encoding(位置编码)的作用是为序列中的词汇添加位置信息。

由于Transformer中Self-Attention是并行计算的,没有顺序信息,因此需要通过Positional Encoding提供单词在序列中的位置和顺序信息。

Positional Encoding为每个词汇对应的嵌入表示添加一个编码向量,这个编码向量用来编码该词汇在序列中的相对位置或绝对位置。这样在Attention计算时,就可以利用词汇的顺序信息。

常用的Positional Encoding有:

固定正弦波编码:使用不同频率的正弦、余弦函数来编码位置。

学习得到的编码:将位置编码作为模型可学习的参数,在训练中自动学习位置信息的编码。

绝对位置与相对位置结合编码:同时考虑单词绝对位置和相对距离。

添加了Positional Encoding后,在Self-Attention的计算中,词汇的表示就包含了其在序列中位置的信息,这样就引入了顺序,网络能够利用词汇之间的距离关系,从而学到序列内的语法结构。

这是Transformer模型区别于CNN和RNN序列建模的一个关键创新点。Positional Encoding为序列提供顺序信息,是Transformer工作的基础。

数学公式

假设输入序列的词汇索引为i,embedding维度为d,则该词汇的位置编码PE(pos,i)可以表示为:
P E ( p o s , i ) = [ s i n ( p o s / 1000 0 2 i / d ) , c o s ( p o s / 1000 0 2 i / d ) ] PE(pos,i) = [sin(pos/10000^{2i/d}), cos(pos/10000^{2i/d})] PE(pos,i)=[sin(pos/100002i/d),cos(pos/100002i/d)]

这里pos是词汇在序列中的位置,从1开始编号。分别使用sin和cos对不同频率进行编码,能够产生不同频率下的震荡形式,以代表位置信息。

那么词汇i的嵌入表示E可以表示为:

E ( i ) = X ( i ) + P E ( p o s , i ) E(i) = X(i) + PE(pos,i) E(i)=X(i)+PE(pos,i)

这里X(i)是词汇i的嵌入向量。将其与位置编码向量相加即得到最后的词汇表示。

在Transformer的self-attention计算中,就将E作为输入,既包含了词汇本身的语义信息,也包含该词汇在序列中的位置信息。

这样,pos就引入了序列顺序,self-attention可以根据词汇位置关系进行分析。

这是Positional Encoding在Transformer架构中赋予序列顺序信息的计算过程。

Masked Self-Attention

在Transformer的解码器(Decoder)中,使用了Masked Self-Attention来保证自注意力(Self-Attention)只聚焦在已生成的词上,避免参照还未生成的词。

具体来说,在解码器的Self-Attention中,对输入序列进行Mask操作,使得一个词汇只能参照该词之前的词的信息,对后面的词进行Mask,注意力权重置为 sehr klein。

举例来说,对输入序列“It is a dog”,在计算第三个词a的Self-Attention时,进行Mask如下:

It is a dog

It is a dog

可以看到,第三个词a只能关注前两个词It is,对后面的词a dog进行Mask。

这样,每个词编码的时候就只能使用前面词的信息,实现了自动回归的顺序生成。

这避免了在编码-解码模型中未来词信息泄露的问题。

相比RNN类模型使用过去状态控制未来信息流动,Mask机制更直接有效。这也使得Transformer可以高效并行计算。

总之,Masked Self-Attention通过对未生成词位置的Mask,实现了顺序生成,是Transformer具有auto-regressive解码能力的关键。

数学公式

设输入序列为X = (x1, x2, …, xn),目标位置为i,则

  1. 密钥(Key)和值(Value)矩阵为:

K = W k X K = WkX K=WkX

V = W v X V = WvX V=WvX

  1. 对i位置进行Mask操作,得到Mask矩阵M:
    M i j = 0 Mij = 0 Mij=0 如果j > i (屏蔽未来信息)
    M i j = − ∞ Mij = -∞ Mij=−∞ 如果j <= i (保留过去信息)

  2. 计算注意力分数:

A t t e n t i o n ( Q i , K , V ) = S o f t m a x ( Q i K T / s q r t ( d k ) ) V Attention(Qi, K, V) = Softmax(QiKT / sqrt(dk))V Attention(Qi,K,V)=Softmax(QiKT/sqrt(dk))V

这里:

Q i = W i X Qi = WiX Qi=WiX 是i位置的查询向量

d k dk dk 是查询向量维度大小

  1. 加入Mask矩阵,得到Masked Attention分数:

M a s k e d A t t e n t i o n ( Q i , K , V ) = S o f t m a x ( ( Q i K T + M ) / s q r t ( d k ) ) V Masked_Attention(Qi, K, V) = Softmax( (QiKT + M) / sqrt(dk) ) V MaskedA​ttention(Qi,K,V)=Softmax((QiKT+M)/sqrt(dk))V

  1. 输出Masked Attention的值作为i位置的表示

这就是Transformer解码器中Masked Self-Attention的计算,它通过屏蔽未来信息来实现顺序生成。

Layer Normalization

Transformer架构中使用了Layer Normalization(层规范化)来提高模型的训练稳定性和收敛速度。

Layer Normalization的计算公式如下:

L N ( x ) = ( x − μ ) / σ LN(x) = (x - μ) / σ LN(x)=(x−μ)/σ

其中,μ和σ分别是x在该层特征上的均值和标准差。

LN的优点是:

  1. 可以加速网络的训练,使得损失更快收敛。

  2. 减少了参数的调节难度,模型对参数变化更鲁棒。

  3. 缓解了梯度消失/爆炸问题。

  4. 标准化操作使得每层输入分布保持一致,有利于训练。

具体到Transformer中,LN的使用带来以下好处:

  1. Self-Attention后使用LN,可以确保序列不同位置均匀分布,利于学习位置表示。

  2. Feed Forward后使用LN,也可以保证输出均匀分布,加速中间表示的学习。

  3. 避免了递归网络中顺序依赖和梯度流动的问题,便于并行计算。

  4. 减少了位置编码对后面层的影响。

总之,Layer Normalization在Transformer结构中使用广泛,是保证模型稳定高效训练的重要组件之一。

它简化了训练过程,也让模型对参数变化更为鲁棒。

代码实现

编码器

import torch
import torch.nn as nn
import math

# 位置编码函数
def get_positional_encoding(max_seq_len, embed_dim):
    # 初始化一个位置编码矩阵
    pos_encoding = torch.zeros(max_seq_len, embed_dim)
    # 计算位置编码值
    for pos in range(max_seq_len):
        for i in range(embed_dim):
            if i % 2 == 0:
                pos_encoding[pos, i] = math.sin(pos / 10000**(2*i/embed_dim)) 
            else:
                pos_encoding[pos, i] = math.cos(pos / 10000**(2*i/embed_dim))
    return pos_encoding

# 自注意力模块
class SelfAttention(nn.Module):
    def __init__(self, embed_dim, heads):
        super(SelfAttention, self).__init__()
        self.embed_dim = embed_dim
        self.heads = heads
        self.head_dim = embed_dim // heads

        # 定义线性变换矩阵
        self.query = nn.Linear(embed_dim, embed_dim)
        self.key = nn.Linear(embed_dim, embed_dim)
        self.value = nn.Linear(embed_dim, embed_dim)
        
        # 定义最后的线性变换
        self.fc_out = nn.Linear(embed_dim, embed_dim)
        
    def forward(self, x):
        # 分头,进行自注意力计算 
        batch_size = x.size(0)
        query = self.query(x).view(batch_size, -1, self.heads, self.head_dim).transpose(1,2)
        key = self.key(x).view(batch_size, -1, self.heads, self.head_dim).transpose(1,2) 
        value = self.value(x).view(batch_size, -1, self.heads, self.head_dim).transpose(1,2)
        
        # 得到注意力分数
        attention = torch.matmul(query, key.transpose(2,3)) / math.sqrt(self.head_dim)
        # 对分数做softmax归一化
        attention = torch.softmax(attention, dim=-1)
        # 和value做矩阵乘法得到 transformer后的张量
        x = torch.matmul(attention, value).transpose(1,2).contiguous()
        x = x.view(batch_size, -1, self.heads * self.head_dim)
        
        # 最后的线性层
        return self.fc_out(x)
        
# 前馈全连接模块        
class FeedForward(nn.Module):
    def __init__(self, embed_dim, feedforward_dim):
        super(FeedForward, self).__init__()
        self.net = nn.Sequential(
            nn.Linear(embed_dim, feedforward_dim),
            nn.ReLU(),
            nn.Linear(feedforward_dim, embed_dim)
        )
    def forward(self, x):
        return self.net(x)

# Transformer编码器       
class Encoder(nn.Module):
    def __init__(self, embed_dim, heads, layers, forward_expansion):
        super(Encoder, self).__init__()
        # 位置编码
        self.positional_encoding = get_positional_encoding(1000, embed_dim)
        
        # 堆叠的编码块
        encoder_layers = nn.TransformerEncoderLayer(embed_dim, heads, forward_expansion, dropout=0.2)
        self.transformer = nn.TransformerEncoder(encoder_layers, layers)
        
    def forward(self, x):
        # 位置编码
        out = self.positional_encoding[:x.size(1)]
        # 通过 transformer 层
        out = self.transformer(x + out)
        return out

  • 1
  • 2
  • 3
  • 4
  • 5
  • 6
  • 7
  • 8
  • 9
  • 10
  • 11
  • 12
  • 13
  • 14
  • 15
  • 16
  • 17
  • 18
  • 19
  • 20
  • 21
  • 22
  • 23
  • 24
  • 25
  • 26
  • 27
  • 28
  • 29
  • 30
  • 31
  • 32
  • 33
  • 34
  • 35
  • 36
  • 37
  • 38
  • 39
  • 40
  • 41
  • 42
  • 43
  • 44
  • 45
  • 46
  • 47
  • 48
  • 49
  • 50
  • 51
  • 52
  • 53
  • 54
  • 55
  • 56
  • 57
  • 58
  • 59
  • 60
  • 61
  • 62
  • 63
  • 64
  • 65
  • 66
  • 67
  • 68
  • 69
  • 70
  • 71
  • 72
  • 73
  • 74
  • 75
  • 76
  • 77
  • 78
  • 79
  • 80

解码器

# 导入模块
import torch
import torch.nn as nn
import math

# 位置编码函数  
def get_positional_encoding(max_seq_len, embed_dim):
    # 初始化位置编码矩阵 
    pos_encoding = torch.zeros(max_seq_len, embed_dim)
    # 计算位置编码  
    for pos in range(max_seq_len):
        for i in range(embed_dim):
            if i % 2 == 0:
                pos_encoding[pos, i] = math.sin(pos / 10000**(2*i/embed_dim))
            else:  
                pos_encoding[pos, i] = math.cos(pos / 10000**(2*i/embed_dim))
    return pos_encoding

# 自注意力模块
class SelfAttention(nn.Module):
    def __init__(self, embed_dim, heads):
        super(SelfAttention, self).__init__()
        self.embed_dim = embed_dim
        self.heads = heads
        self.head_dim = embed_dim // heads
        # 定义线性层
        self.query = nn.Linear(embed_dim, embed_dim)
        self.key = nn.Linear(embed_dim, embed_dim)
        self.value = nn.Linear(embed_dim, embed_dim)
        self.fc_out = nn.Linear(embed_dim, embed_dim)
        
    def forward(self, x):
        batch_size = x.size(0)
        # 分头处理
        query = self.query(x).view(batch_size, -1, self.heads, self.head_dim).transpose(1,2)
        key = self.key(x).view(batch_size, -1, self.heads, self.head_dim).transpose(1,2)
        value = self.value(x).view(batch_size, -1, self.heads, self.head_dim).transpose(1,2)   
        # 得到注意力得分  
        attention = torch.matmul(query, key.transpose(2,3)) / math.sqrt(self.head_dim)
        attention = torch.softmax(attention, dim=-1) 
        # 计算Transformer输出
        x = torch.matmul(attention, value).transpose(1,2).contiguous()
        x = x.view(batch_size, -1, self.heads * self.head_dim) 
        return self.fc_out(x)
        
# 前馈全连接模块
class FeedForward(nn.Module):
    def __init__(self, embed_dim, feedforward_dim):
        super(FeedForward, self).__init__()
        self.net = nn.Sequential(
            nn.Linear(embed_dim, feedforward_dim),
            nn.ReLU(),
            nn.Linear(feedforward_dim, embed_dim)
        )
    def forward(self, x):
        return self.net(x)
        
# Transformer解码器       
class Decoder(nn.Module):
    def __init__(self, embed_dim, heads, layers, forward_expansion):
        super(Decoder, self).__init__()
        self.positional_encoding = get_positional_encoding(1000, embed_dim)
        # 使用 Masked Self-Attention
        decoder_layer = nn.TransformerDecoderLayer(embed_dim, heads, forward_expansion, dropout=0.2)
        self.transformer = nn.TransformerDecoder(decoder_layer, layers)
        
    def forward(self, x, encoder_out):
        out = self.positional_encoding[:x.size(1)]
        out = self.transformer(x + out, encoder_out)
        return out

  • 1
  • 2
  • 3
  • 4
  • 5
  • 6
  • 7
  • 8
  • 9
  • 10
  • 11
  • 12
  • 13
  • 14
  • 15
  • 16
  • 17
  • 18
  • 19
  • 20
  • 21
  • 22
  • 23
  • 24
  • 25
  • 26
  • 27
  • 28
  • 29
  • 30
  • 31
  • 32
  • 33
  • 34
  • 35
  • 36
  • 37
  • 38
  • 39
  • 40
  • 41
  • 42
  • 43
  • 44
  • 45
  • 46
  • 47
  • 48
  • 49
  • 50
  • 51
  • 52
  • 53
  • 54
  • 55
  • 56
  • 57
  • 58
  • 59
  • 60
  • 61
  • 62
  • 63
  • 64
  • 65
  • 66
  • 67
  • 68
  • 69
  • 70
声明：本文内容由网友自发贡献，版权归原作者所有，本站不承担相应法律责任。如您发现有侵权的内容，请联系我们。转载请注明出处：【wpsshop博客】
推荐阅读
相关标签

Copyright © 2003-2013 www.wpsshop.cn 版权所有，并保留所有权利。

  

闽ICP备14008679号