【CV】膨胀卷积详解以及时间卷积网络TCN论文笔记和源码实现_temporal convolutional networks for action segment

这篇博文分为两部分。第一部分详细讲解了TCN模型（Temporal Convolutional Network）中涉及的1D卷积，因果卷积，膨胀卷积中设计的计算，非常值得一看，有醍醐灌顶的作用。第二部分是TCN的论文。

---

论文名称：Temporal Convolutional Networks for Action Segmentation and Detection
论文下载：https://arxiv.org/abs/1611.05267
论文年份：2016
论文被引：738（2022/04/11）
论文代码：https://github.com/colincsl/TemporalConvolutionalNetworks

---

TCN Explanation

1D Convolutional Network

一维卷积网络将 3 维张量作为输入，并输出 3 维张量。我们 TCN 实现的输入张量具有形状 (batch_size, input_length, input_channels)，输出张量具有形状 (batch_size, input_length, output_channels)。由于 TCN 中的每一层都具有相同的输入和输出长度，因此只有输入和输出张量的第三维不同。在单变量情况下，input_channels 和 output_channels 都将等于 1。在更一般的多变量情况下，input_channels 和 output_channels 可能不同，因为我们可能不想预测输入序列的每个分量。

要了解单个层如何将其输入转换为输出，让我们看一下批处理中的一个元素（批处理中的每个元素都会发生相同的过程）。让我们从最简单的情况开始，其中 input_channels 和 output_channels 都等于 1。下图显示了如何计算输出张量的一个元素。

我们可以看到，为了计算输出的一个元素，我们查看输入的长度为 kernel_size 的一系列连续元素。在上面的示例中，kernel_size = 3。为了获得输出，我们将输入的子序列与相同长度的学习权重的核向量进行点积。为了获得输出的下一个元素，应用相同的过程，但是输入序列的 kernel_size 大小的窗口向右移动一个元素（对于这个预测模型，步幅始终设置为 1）。注意，同一组卷积核权重将用于计算一个卷积层的每个输出。下图显示了两个连续的输出元素及其各自的输入子序列。

为了使可视化更简单，不再显示具有卷积核向量的点积，而是针对具有相同卷积核权重的每个输出元素。为了确保输出序列与输入序列具有相同的长度，应用了一些零填充。这意味着将额外的零值添加到输入张量的开头或结尾，以确保输出具有所需的长度。

现在看看有多个输入通道的情况，即 input_channels > 1。在这种情况下，对每个输入通道重复上述过程，但每次使用不同的卷积核。该过程将会有 input_channels 个中间输出向量，以及 kernel_size * input_channels 个卷积核权重。然后，将所有的中间输出向量相加得到最终的输出向量。从某种意义上说，这相当于一个二维卷积，其输入张量为 (input_size, input_channels)，卷积核为 (kernel_size, input_channels)，如下图所示。它仍然是 1D，因为窗口仅沿单个轴移动，但我们在每一步都有一个 2D 卷积，因为我们使用的是 2 维卷积核矩阵。

上例中，input_channels = 2。其过程是一个长为 kernel_size，宽为 input_channels 的卷积核矩阵沿 一个长为 input_length，宽为 input_channels 的序列滑动，而不是在 1 维输入序列上滑动。

如果 input_channels 和 output_channels 都大于 1，则只需对具有不同卷积核矩阵的每个输出通道重复上述过程。然后将输出向量堆叠在一起，形成形状为 (input_length, output_channels) 的输出张量。在这种情况下，卷积核权重的数量等于 kernel_size * input_channels * output_channels。

两个变量 input_channels 和 output_channels 取决于层在网络中的位置。第一层的 input_channels = input_size，最后一层的 output_channels = output_size。所有其他层将使用 num_filters 给出的中间通道数量。

Causal Convolution

对于因果关系的卷积层，对于 $0,...,inpu{t}_{l}ength-1$ 中的每个 $i$，输出序列的第 $i$ 个元素可能仅取决于索引为 { 0 , . . . , i } \{0, ..., i\} {0,...,i} 的输入序列的元素。换句话说，输出序列中的一个元素只能依赖于输入序列中它之前的元素。如前所述，为了确保输出张量与输入张量具有相同的长度，需要零填充。如果只在输入张量的左侧应用零填充，那么将确保因果卷积。要理解这一点，请考虑最右边的输出元素。鉴于输入序列的右侧没有填充，它依赖的最后一个元素是输入的最后一个元素。现在考虑输出序列的倒数第二个输出元素。与最后一个输出元素相比，它的卷积核窗口向左移动了一个，这意味着它在输入序列中最右边的依赖关系是输入序列的倒数第二个元素。通过归纳可知，对于输出序列中的每个元素，其在输入序列中的最新依赖项具有与其自身相同的索引。下图显示了 input_length = 4 且 kernel_size = 3 的示例。

由上图可知，通过 2 个元素的左侧零填充，可以在遵守因果关系规则的同时实现相同的输出长度。在没有膨胀的情况下，维持输入长度所需的零填充元素的数量始终等于 kernel_size – 1。

Dilation Convolution

预测模型的一个理想质量是输出中特定元素的值取决于输入中的所有先前元素，即索引小于或等于自身的所有元素。当感受野（即影响输出的特定元素的原始输入的元素集）为 input_length 时，可以实现这一点。我们也称其为 完整的历史覆盖 (full history coverage)。正如我们之前所见，一个传统的卷积层在输出中生成一个元素，该元素取决于输入的 kernel_size 元素，其索引小于或等于其自身。例如，如果 kernel_size = 3，则输出中的第 5 个元素将取决于输入的第 3、4、5 个元素。当将多层堆叠在一起时，这种范围就会扩大。在下图中，通过堆叠两层 kernel_size = 3 的层，得到了大小为 5 的感受野。使用卷积网络而不是循环网络可以提高性能，因为它允许并行计算输出。

更一般地，具有 $n$ 层和 kernel_size = $k$ 的一维卷积网络的感受野 $r$ 的计算公式为：

$$r=1+n\ast (k-1)$$

要知道全覆盖需要多少层，我们可以将感受野大小设置为 input_length = $l$ 并求解层数 $n$（如果是非整数值，需要四舍五入）：

$$n=\lceil (l-1)(k-1)\rceil$$

这意味着，给定一个固定的 kernel_size，完整历史覆盖所需的层数与输入张量的长度呈线性关系，这将导致网络变得非常深非常快，从而导致模型具有非常大量的参数需要更长的时间来训练。此外，大量层已被证明会导致与损失函数梯度相关的退化问题。在保持层数相对较小的同时增加感受野大小的一种方法是将膨胀引入卷积网络。

卷积层上下文中的膨胀（Dilation）是指输入序列元素之间的距离，这些元素用于计算输出序列的一个元素。因此，传统的卷积层可以看作是 1-dilated 层，因为 1 个输出值的输入元素是相邻的。

下图显示了一个 2-dilated 层的示例，其中 input_length = 4，kernel_size = 3。

与 1-dilated 的情况相比，该层的感受野大小为 5 而不是 3。更一般地，卷积核大小为 $k$ 的 $d$-dilated 层的感受野大小为 $1+d\ast (k-1)$。如果 d 是固定的，这仍然需要一个与输入张量长度呈线性关系的数字来实现完全的感受野覆盖（我们只是减小了常数）。

这个问题可以通过随着向上移动层而以指数方式增加 d 的值来解决。为此，我们选择一个常数 dilation_base 整数 b，它将让我们计算特定层的膨胀大小 $d$ 作为其下方层数 $i$ 的函数，如 $d=b^i$。下图显示了一个 input_length = 10、kernel_size = 3 和 dilation_base = 2 的网络，它产生了 3 个膨胀卷积层以实现全覆盖。

WaveNet论文中的说明，可以帮助理解感受野：

这里只展示了影响最后一个输出值的输入的情形。同样，仅显示最后一个输出值所需的零填充元素。显然，最后一个输出值取决于整个输入覆盖范围。一般来说，每个额外的层都会在当前感受野宽度上增加一个 $d\ast (k-1)$ 的值，其中 $d$ 计算为 $d=b^i$，$i$ 表示新层之下的层数。因此，具有基数 $b$ 的指数膨胀、卷积核大小 $k$ 和层数 $n$ 的 TCN 的感受野的宽度 $w$ 由下式给出：

$$w=1+\sum _{i=0}^{n-1}(k-1)\cdot b^i=1+(k+1)\cdot \frac{b^n-1}{b-1}$$

然而，根据 b 和 k 的值，这个感受野可能有“空洞”。考虑以下 dilation_base = 3 和卷积核大小为 2 的网络：

感受野确实覆盖了大于输入大小的范围。然而，感受野中有空洞。也就是说，输入序列中存在输出值不依赖的元素（如上图红色所示）。为了解决这个问题，我们需要将卷积核大小增加到 3，或者将膨胀系数减少到 2。一般来说，对于没有空洞的感受野，卷积核大小 k 必须至少与膨胀系数 d 一样大。

考虑到这些观察，我们可以计算出网络需要多少层才能覆盖完整的历史记录。给定卷积核大小 $k$、膨胀系数 $b$，其中 $k\ge b$，输入长度为 $l$，对于完整的历史覆盖，必须满足以下不等式：

$$1+(k-1)\cdot \frac{b^n-1}{b-1}\ge l$$

我们可以求解 $n$ 并获得所需的最小层数为：

$$n=\lceil lo{g}_b(\frac{(l-1)(b-1)}{(k-1)}+1)\rceil$$

我们可以看到，层数现在在输入长度上是对数的，而不是线性的。这是一个显着的改进，可以在不牺牲感受野覆盖范围的情况下实现。

现在唯一需要指定的是每层所需的零填充元素的数量。给定一个给定卷积核大小 $k$、膨胀系数 $b$和当前层以下的 $i$ 层数，则当前层所需的零填充元素数 $p$ 计算如下：

$$p=b^i\cdot (k-1)$$

Basic TCN Overview

给定 input_length、kernel_size、dilation_base 和完整历史覆盖所需的最小层数，基本的 TCN 网络看起来像这样：

Forecasting

到目前为止，我们只讨论了输入序列和输出序列，而没有讨论它们之间的关系。在预测的上下文中，我们希望预测未来时间序列的下一个元素。为了训练 TCN 网络进行预测，训练集将由（输入序列、目标序列）对给定时间序列的大小相等的子序列组成。目标系列将是相对于其各自的输入系列向前移动一定数量的输出长度的序列。这意味着长度为 input_length 的目标序列包含其各自输入序列的最后一个 (input_length - output_length) 元素作为第一个元素，并且在输入序列的最后一个元素之后的 output_length 元素作为其最终元素。在预测的上下文中，这意味着可以使用这种模型预测的最大预测范围等于 output_length。使用滑动窗口方法，可以从一个时间序列中创建许多重叠的输入和目标序列对。

Improvements to the Model

S. Bai et al. 建议对基本 TCN 架构进行一些改进以提高性能，这将在本节中讨论，即残差连接、正则化和激活函数。

Residual Blocks

我们对之前介绍的基本模型所做的最大修改是将模型的基本构建块从简单的一维因果卷积层更改为由具有相同膨胀因子和残差连接的 2 层组成的残差块。让我们考虑一个来自基本模型的膨胀因子 d = 2 和卷积核大小 k = 3 的层，看看它如何转化为改进模型的残差块。

变为

两个卷积层的输出将被添加到残差块的输入中，以产生下一个块的输入。对于网络的所有内部块，即除了第一个和最后一个之外的所有块，输入和输出通道宽度相同，即 num_filters 数量相同。由于第一个残差块的第一个卷积层和最后一个残差块的第二个卷积层可能具有不同的输入和输出通道宽度，因此可能需要调整残差张量的宽度，这是使用 1×1 卷积完成的。（注意：1x1 卷积的作用之一就是调整通道宽度）

此更改会影响完全覆盖所需的最小层数的计算。现在我们必须考虑需要多少残差块才能实现完整的感受野覆盖。向 TCN 添加残差块会比添加基本因果层增加两倍的感受野宽度，因为它包括 2 个这样的层。因此，具有膨胀系数 b 的 TCN 的感受野 r 的总大小、k ≥ b 的卷积核大小 k 和残差块的数量 n 可以计算为：

$$r=1+\sum _{i=0}^{n-1}2\cdot (k-1)\cdot b^i=1+2\cdot (k-1)\cdot \frac{b^n-1}{b-1}$$

这导致最小数量的残差块 n 用于 input_length = l 的完整历史覆盖

$$n=\lceil lo{g}_b(\frac{(l-1)(b-1)}{(k-1)\cdot 2}+1)\rceil$$

Activation, Normalization, Regularization

为了使 TCN 不仅仅是一个过于复杂的线性回归模型，需要在卷积层之上添加激活函数以引入非线性。 ReLU 激活被添加到两个卷积层之后的残差块中。

为了对隐藏层的输入进行归一化（这可以抵消梯度爆炸等问题），将权重归一化应用于每个卷积层。

为了防止过拟合，在每个残差块的每个卷积层之后通过 dropout 引入正则化。下图显示了最终的残差块。

第二个 ReLU 单元中的星号表示它存在于除最后一层之外的每一层，因为我们希望最终输出也能够采用负值（这与论文中概述的架构不同）。

Final Model

下图显示了最终的 TCN 模型，其中 l 等于 input_length，k 等于 kernel_size，b 等于 dilation_base，k ≥ b ，并且具有完整历史覆盖 n 的最小残差块数，其中 n 可以从其他值计算，如上所述。

Example

看一个示例，说明如何使用 TCN 架构，使用 Darts 库来预测时间序列。

首先，需要一个时间序列来训练和评估模型。为此，使用了一个 Kaggle 数据集，其中包含来自西班牙的每小时能源生产数据。更具体地说，我们选择预测径流水力发电。此外，为了减少问题的计算密集度，平均每天的能量产生以获得每日时间序列。

from darts import TimeSeries
from darts.dataprocessing.transformers import 
MissingValuesFiller
import pandas as pd

df = pd.read_csv('energy_dataset.csv', delimiter=",")
df['time'] = pd.to_datetime(df['time'], utc=True)
df['time']= df.time.dt.tz_localize(None)

df_day_avg = 
df.groupby(df['time'].astype(str).str.split(" ").str[0]).mean().reset_index()

value_filler = MissingValuesFiller()
series = 
value_filler.transform(TimeSeries.from_dataframe(df_day_avg, 'time', ['generation hydro run-of-river and poundage']))

series.plot()
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17

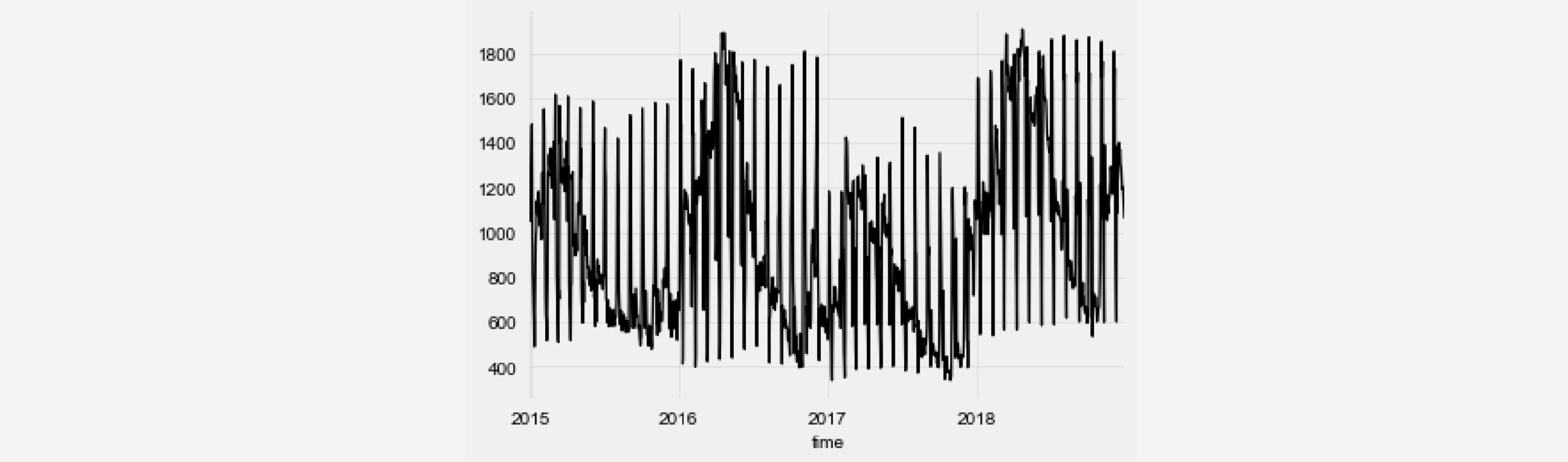
可以看到，除了每年的季节性变化之外，能源生产中还会出现每月定期出现的“峰值”。由于 TCN 模型支持多个输入通道，我们可以在当前时间序列中添加额外的时间序列组件，以编码当前日期。这可以帮助 TCN 模型更快地收敛。

series = series.add_datetime_attribute('day', one_hot=True)
1

现在将数据拆分为训练和验证组件并执行标准化。

from darts.dataprocessing.transformers import Scaler

train, val = 
series.split_after(pd.Timestamp('20170901'))

scaler = Scaler()
train_transformed = scaler.fit_transform(train)
val_transformed = scaler.transform(val)
series_transformed = scaler.transform(series)
1
2
3
4
5
6
7
8
9

现在是时候创建和训练 TCN 模型了。请注意，上述架构描述中出现的所有粗体变量名称都可以用作 Darts TCN 实现的构造函数的参数。 output_length 参数设置为 7，因为我们要执行每周预测。在训练模型时，我们仅将训练序列的第一个组件指定为 target_series，因为我们不想预测我们之前添加的辅助时间序列。我们尝试了几种不同的超参数组合，但大多数值都是随意选择的。

from darts.models import TCNModel

model = TCNModel(
    input_size=train.width,
    n_epochs=20, 
    input_length=365,
    output_length=7, 
    dropout=0, 
    dilation_base=2, 
    weight_norm=True,
    kernel_size=7,
    num_filters=4,
    random_state=0
)

model.fit(
    training_series=train_transformed,
    target_series=train_transformed['0'],
    val_training_series=val_transformed,
    val_target_series=val_transformed['0'], 
verbose=True
)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22

为了评估模型，我们希望在验证集中的许多不同时间点上使用 7 天的预测范围来测试其性能。为此，我们使用了 Darts 的历史回测功能。请注意，模型为每个预测提供了新的输入数据，但它从未被重新训练。为了节省时间，我们将步幅设置为 5。

pred_series = model.backtest(
    series_transformed,
    target_series=series_transformed['0'],
    start=pd.Timestamp('20170901'), 
    forecast_horizon=7,
    stride=5,
    retrain=False,
    verbose=True,
    use_full_output_length=True
)
1
2
3
4
5
6
7
8
9
10

将 TCN 模型的历史预测值与真实数据点可视化并计算 R2 分数。

from darts.metrics import r2_score
import matplotlib.pyplot as plt

series_transformed[900:]['0'].plot(label='actual')
pred_series.plot(label=('historic 7 day forecasts'))
r2_score_value = r2_score(series_transformed['0'], pred_series)

plt.title('R2:' + str(r2_score_value))
plt.legend()
1
2
3
4
5
6
7
8
9

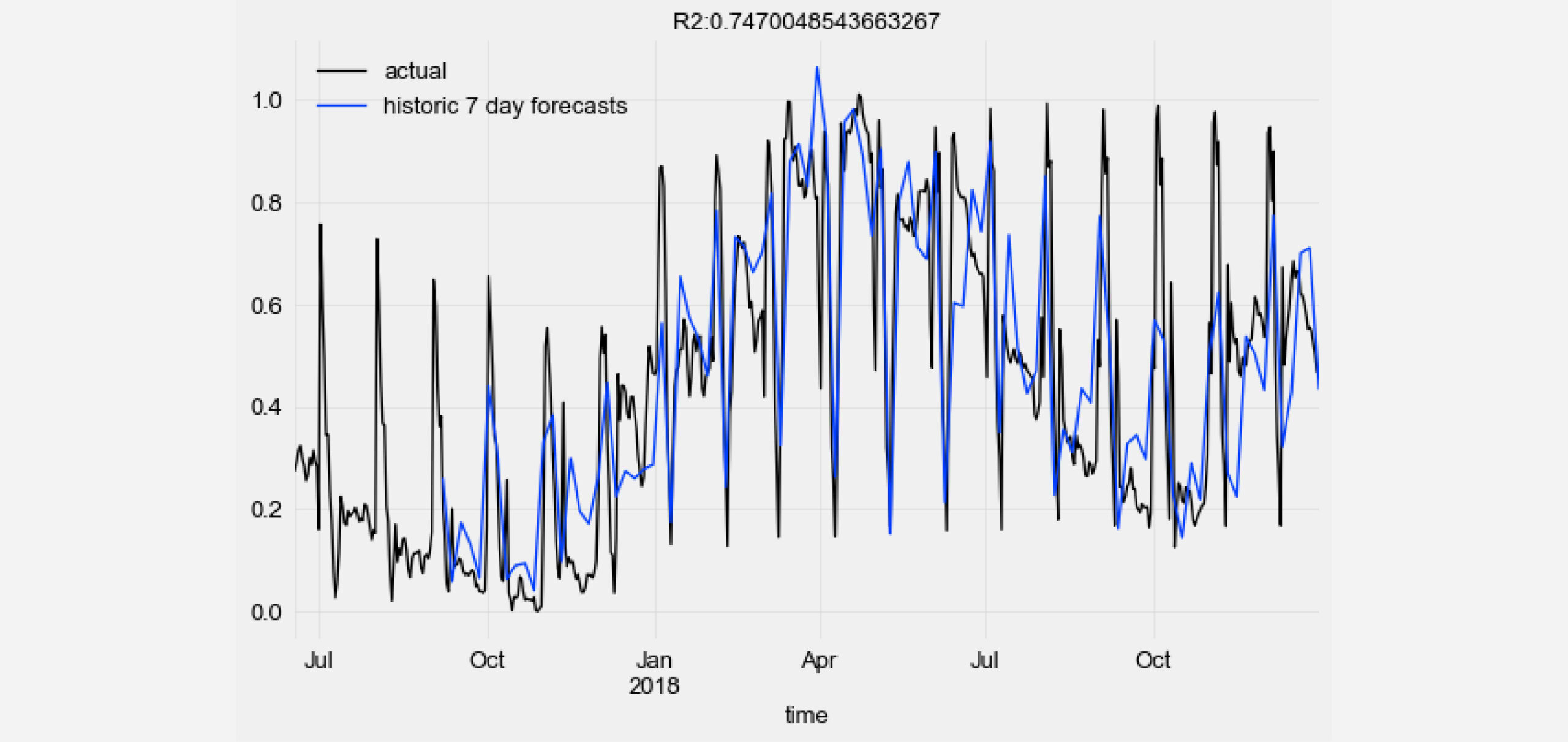
有关更多详细信息和其他示例，请查看 GitHub 上的 TCN 示例笔记本。

在大多数情况下，序列建模中的深度学习仍然与循环神经网络架构广泛相关。但研究表明，在预测性能和效率方面，TCN 在许多任务中都可以胜过这些类型的模型。在本文中，我们探讨了如何根据简单的构建块（例如 1D 卷积层、膨胀和残差连接）来理解这个有前途的模型，以及它们如何组合在一起。此外，我们成功地应用了 TCN 架构的当前 Darts 实现来预测真实世界的时间序列。

TCN Keras Source Code

# from https://github.com/philipperemy/keras-tcn


import keras.backend as K
import keras.layers
from keras import optimizers
from keras.engine.topology import Layer
from keras.layers import Activation, Lambda
from keras.layers import Conv1D, SpatialDropout1D
from keras.layers import Convolution1D, Dense
from keras.models import Input, Model
from typing import List, Tuple


def channel_normalization(x):
    # type: (Layer) -> Layer
    """ Normalize a layer to the maximum activation
    This keeps a layers values between zero and one.
    It helps with relu's unbounded activation
    Args:
        x: The layer to normalize
    Returns:
        A maximal normalized layer
    """
    max_values = K.max(K.abs(x), 2, keepdims=True) + 1e-5
    out = x / max_values
    return out


def wave_net_activation(x):
    # type: (Layer) -> Layer
    """This method defines the activation used for WaveNet
    described in https://deepmind.com/blog/wavenet-generative-model-raw-audio/
    Args:
        x: The layer we want to apply the activation to
    Returns:
        A new layer with the wavenet activation applied
    """
    tanh_out = Activation('tanh')(x)
    sigm_out = Activation('sigmoid')(x)
    return keras.layers.multiply([tanh_out, sigm_out])


def residual_block(x, s, i, activation, nb_filters, kernel_size, padding, dropout_rate=0, name=''):
    # type: (Layer, int, int, str, int, int, float, str) -> Tuple[Layer, Layer]
    """Defines the residual block for the WaveNet TCN
    Args:
        x: The previous layer in the model
        s: The stack index i.e. which stack in the overall TCN
        i: The dilation power of 2 we are using for this residual block
        activation: The name of the type of activation to use
        nb_filters: The number of convolutional filters to use in this block
        kernel_size: The size of the convolutional kernel
        padding: The padding used in the convolutional layers, 'same' or 'causal'.
        dropout_rate: Float between 0 and 1. Fraction of the input units to drop.
        name: Name of the model. Useful when having multiple TCN.
    Returns:
        A tuple where the first element is the residual model layer, and the second
        is the skip connection.
    """

    original_x = x
    conv = Conv1D(filters=nb_filters, kernel_size=kernel_size,
                  dilation_rate=i, padding=padding,
                  name=name + '_dilated_conv_%d_tanh_s%d' % (i, s))(x)
    if activation == 'norm_relu':
        x = Activation('relu')(conv)
        x = Lambda(channel_normalization)(x)
    elif activation == 'wavenet':
        x = wave_net_activation(conv)
    else:
        x = Activation(activation)(conv)

    x = SpatialDropout1D(dropout_rate, name=name + '_spatial_dropout1d_%d_s%d_%f' % (i, s, dropout_rate))(x)

    # 1x1 conv.
    x = Convolution1D(nb_filters, 1, padding='same')(x)
    res_x = keras.layers.add([original_x, x])
    return res_x, x


def process_dilations(dilations):
    def is_power_of_two(num):
        return num != 0 and ((num & (num - 1)) == 0)

    if all([is_power_of_two(i) for i in dilations]):
        return dilations

    else:
        new_dilations = [2 ** i for i in dilations]
        # print(f'Updated dilations from {dilations} to {new_dilations} because of backwards compatibility.')
        return new_dilations


class TCN:
    """Creates a TCN layer.
        Args:
            input_layer: A tensor of shape (batch_size, timesteps, input_dim).
            nb_filters: The number of filters to use in the convolutional layers.
            kernel_size: The size of the kernel to use in each convolutional layer.
            dilations: The list of the dilations. Example is: [1, 2, 4, 8, 16, 32, 64].
            nb_stacks : The number of stacks of residual blocks to use.
            activation: The activations to use (norm_relu, wavenet, relu...).
            padding: The padding to use in the convolutional layers, 'causal' or 'same'.
            use_skip_connections: Boolean. If we want to add skip connections from input to each residual block.
            return_sequences: Boolean. Whether to return the last output in the output sequence, or the full sequence.
            dropout_rate: Float between 0 and 1. Fraction of the input units to drop.
            name: Name of the model. Useful when having multiple TCN.
        Returns:
            A TCN layer.
        """

    def __init__(self,
                 nb_filters=64,
                 kernel_size=2,
                 nb_stacks=1,
                 dilations=None,
                 activation='norm_relu',
                 padding='causal',
                 use_skip_connections=True,
                 dropout_rate=0.0,
                 return_sequences=True,
                 name='tcn'):
        self.name = name
        self.return_sequences = return_sequences
        self.dropout_rate = dropout_rate
        self.use_skip_connections = use_skip_connections
        self.activation = activation
        self.dilations = dilations
        self.nb_stacks = nb_stacks
        self.kernel_size = kernel_size
        self.nb_filters = nb_filters
        self.padding = padding

        # backwards incompatibility warning.
        # o = tcn.TCN(i, return_sequences=False) =>
        # o = tcn.TCN(return_sequences=False)(i)

        if padding != 'causal' and padding != 'same':
            raise ValueError("Only 'causal' or 'same' paddings are compatible for this layer.")

        if not isinstance(nb_filters, int):
            print('An interface change occurred after the version 2.1.2.')
            print('Before: tcn.TCN(i, return_sequences=False, ...)')
            print('Now should be: tcn.TCN(return_sequences=False, ...)(i)')
            print('Second solution is to pip install keras-tcn==2.1.2 to downgrade.')
            raise Exception()

    def __call__(self, inputs):
        if self.dilations is None:
            self.dilations = [1, 2, 4, 8, 16, 32]
        x = inputs
        x = Convolution1D(self.nb_filters, 1, padding=self.padding, name=self.name + '_initial_conv')(x)
        skip_connections = []
        for s in range(self.nb_stacks):
            for i in self.dilations:
                x, skip_out = residual_block(x, s, i, self.activation, self.nb_filters,
                                             self.kernel_size, self.padding, self.dropout_rate, name=self.name)
                skip_connections.append(skip_out)
        if self.use_skip_connections:
            x = keras.layers.add(skip_connections)
        x = Activation('relu')(x)

        if not self.return_sequences:
            output_slice_index = -1
            x = Lambda(lambda tt: tt[:, output_slice_index, :])(x)
        return x


def model_tcn(embedding_matrix):
    
    inp = Input(shape=(maxlen,))
    x = Embedding(max_features, embed_size, weights=[embedding_matrix], trainable=False)(inp)
    x = SpatialDropout1D(0.1)(x)
    x = TCN(128,dilations = [1, 2, 4], return_sequences=True, activation = 'wavenet',name = 'tnc1')(x)
    x = TCN(64,dilations = [1, 2, 4], return_sequences=True, activation = 'wavenet',name = 'tnc2')(x)
    avg_pool = GlobalAveragePooling1D()(x)
    max_pool = GlobalMaxPooling1D()(x)
    
    conc = concatenate([avg_pool, max_pool])
    conc = Dense(16, activation="relu")(conc)
    conc = Dropout(0.1)(conc)
    outp = Dense(1, activation="sigmoid")(conc)    

    model = Model(inputs=inp, outputs=outp)
    model.compile(loss='binary_crossentropy', optimizer='adam', metrics=[f1])
    
    return model
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188

References

https://unit8.com/resources/temporal-convolutional-networks-and-forecasting/
https://www.kaggle.com/code/christofhenkel/temporal-convolutional-network/notebook

---

Temporal Convolutional Networks for Action Segmentation and Detection

Abstract

The ability to identify and temporally segment finegrained human actions throughout a video is crucial for robotics, surveillance, education, and beyond. Typical approaches decouple this problem by first extracting local spatiotemporal features from video frames and then feeding them into a temporal classifier that captures high-level temporal patterns. We introduce a new class of temporal models, which we call Temporal Convolutional Networks (TCNs), that use a hierarchy of temporal convolutions to perform fine-grained action segmentation or detection. Our Encoder-Decoder TCN uses pooling and upsampling to efficiently capture long-range temporal patterns whereas our Dilated TCN uses dilated convolutions. We show that TCNs are capable of capturing action compositions, segment durations, and long-range dependencies, and are over a magnitude faster to train than competing LSTM-based Recurrent Neural Networks. We apply these models to three challenging fine-grained datasets and show large improvements over the state of the art.

识别和在时间上分割整个视频中细粒度的人类行为的能力对于机器人、监控、教育等领域至关重要。典型的方法首先从视频帧中提取局部时空特征，然后将它们输入到捕获高级时间模式的时间分类器中，从而解耦（decouple）这个问题。我们引入了一类新的时间模型，我们称之为时间卷积网络 (Temporal Convolutional Networks，TCN)，它使用时间卷积的层次结构来执行细粒度的动作分割或检测。我们的编码器-解码器 TCN 使用池化和上采样来有效地捕获长期时间模式，而我们的膨胀 TCN 使用膨胀卷积（dilated convolutions）。我们表明，TCN 能够捕获动作组合、片段持续时间和长期依赖关系，并且比竞争的基于 LSTM 的循环神经网络的训练速度快一个数量级。我们将这些模型应用于三个具有挑战性的细粒度数据集，并展示了对现有技术的巨大改进。

1. Introduction

**动作分割（Action segmentation）**对于从协作机器人到日常生活活动分析的应用至关重要。给定一个视频，目标是在时间上同时分割每个动作，并对每个组成片段进行分类。在文献中，这项任务通过动作分割或检测来完成。我们专注于模拟情境活动——如在厨房或监控系统中——这些活动由几十个动作在几分钟内组成。这些动作，比如切西红柿和剥黄瓜，彼此之间往往只有细微的区别。

当前的方法将此任务解耦为提取低级时空特征（spatiotemporal features）和应用高级时间分类器（temporal classifiers）。虽然对前者进行了广泛的工作，但最近的时间模型仅限于滑动窗口动作检测器（sliding window action detectors） [25、27、20]，它们通常不能捕获长期时间模式（long-range temporal patterns）；分割模型（segmental model） [24, 15, 23]，捕获分段（segment）内属性但假设条件独立，从而忽略长期潜在依赖关系；循环模型（recurrent model） [27, 9]，可以捕捉潜在的时间模式但难以解释，根据经验发现其注意力跨度有限 [27]，并且难以正确训练 [21]。

在本文中，我们讨论了一类时间序列模型，我们称之为时间卷积网络 (Temporal Convolutional Networks，TCNs)，它通过使用时间卷积滤波器的层次结构捕获长期模式来克服前面的缺点。我们提出了两种类型的 TCN：首先，我们的 Encoder-Decoder TCN (ED-TCN) 仅使用时间卷积、池化和上采样的层次结构，但可以有效地捕获长期时间模式。 ED-TCN 的层数相对较少（例如，编码器中的 3 个），但每一层都包含一组长卷积滤波器。其次，Dilated TCN 使用膨胀卷积而不是池化和上采样，并在层之间添加跳跃连接。这是对最近的 WaveNet [33] 模型的改进，它与我们的 ED-TCN 有相似之处，但它是为语音处理任务而开发的。 Dilated TCN 有更多层，但每个层都使用仅在少量时间步上运行的膨胀滤波器。根据经验，我们发现两个 TCN 都能够捕获分割模型的特征，例如动作持续时间和分段之间的成对转换，以及类似于循环模型的长期时间模式。这些模型往往优于我们的双向 LSTM (Bi-LSTM) [5] 基线，并且训练速度快一个数量级。特别是 ED-TCN 产生的过度分割错误比其他模型少得多。

在文献中，我们的任务被称为动作分割（action segmentation） [7, 8, 6, 14, 28, 15, 9] 或动作检测（action detection） [27, 19, 20, 24]。尽管实际上是相同的问题，但分割论文中的时间方法往往与检测论文不同，评估它们的指标也是如此。在本文中，我们评估了针对这两个任务的数据集，并提出了分段 F1 分数（segmental F1 score），我们定性地发现它比常见指标更适用于分割和检测的现实问题。我们使用为动作检测而设计的MERL Shopping，为动作分割而设计的Georgia Tech Egocentric Activities，以及已用于两者的50 Salads。

2. Related Work

动作分割方法预测视频中每一帧发生的动作，检测方法输出一个稀疏集合的动作片段，其中一个片段由开始时间、结束时间和类标签定义。通过简单地添加或删除空/背景段，可以在给定的分割和一组检测之间进行转换。

动作检测：许多细粒度检测论文对空间或时空特征使用基于滑动窗口的检测方法。[25] 在 MPII Cooking 数据集上使用 Dense Trajectories [36] 和人体姿势特征。在每一帧，他们为许多候选片段长度评估滑动 SVM，并执行非最大抑制以找到一小组动作预测。[20] 使用以对象为中心的特征表示，迭代地解析对象位置和空间配置，并将其应用于 MPII Cooking 和 ICPR 2012 Kitchen 数据集。他们的方法使用密集轨迹特征作为滑动窗口检测方法的输入，分段间隔为 30、60 和 90 帧。

[27] 通过将每帧 CNN 特征输入 LSTM 模型并将类似于非最大抑制的方法应用于 LSTM 输出来对此进行了改进。我们使用 Singh 提出的数据集 MERL 购物，并证明我们的方法优于他们基于 LSTM 的检测模型。最近， [24]引入了一种分段方法，该方法结合了一种语言模型，该模型捕获了分段之间的成对转换，以及一个持续时间模型，该模型确保了分段具有适当的长度。在实验中，我们表明我们的模型能够捕获这两个部分。

其中一些数据集，包括 MPII Cooking，已用于分类（例如，[3, 38]），但是，此任务假设每个片段的边界是已知的。

动作分割：分割论文倾向于使用捕获高级模式的时间模型，例如 RNN 或条件随机场 (Conditional Random Fields，CRF)。[8, 7, 6] 使用了一个分段模型，该模型在每个动作的开始和结束时捕获对象状态（例如，面包在涂抹果酱之前和之后的外观）。他们将他们的工作应用于我们在实验中使用的佐治亚理工学院以自我为中心的活动 (GTEA) 数据集。[28] 使用一组 CNN 在 GTEA 数据集上提取以自我为中心的特定特征，但没有使用高级时间模型。[15] 介绍了一个带有约束分段模型的时空 CNN，他们将其应用于 50 份沙拉。他们的模型通过限制候选片段的最大数量来减少动作过度分割错误的数量。我们展示了我们的 TCN 产生的过度分割错误更少。 [13, 14] 在密集轨迹特征上使用隐马尔可夫模型对动作进行建模，他们将高级语法应用于 50 份沙拉。其他工作着眼于动作分割的半监督方法[9]，减少了所需标注的数量并在与基于 RNN 的模型一起使用时提高了性能。他们的方法有可能与 TCN 一起使用以提高性能。

大规模识别：在用于大规模视频分类和检测的时空模型方面已经开展了大量工作 [30、10、11、26、32、22、18]。这些专注于从短序列图像中捕获对象和场景级信息，因此被认为与我们的工作正交，后者专注于捕获更远距离的时间信息。我们模型的输入可以是时空 CNN 的输出。

其他相关模型：TCN 与最近的语义分割工作有相似之处，后者使用全卷积 CNN 来计算给定图像的每像素对象标记。 Encoder-Decoder TCN 与 SegNet [2] 最相似，而 Dilated TCN 与 Multi-Scale Context 模型 [37] 最相似。 TCNs 也与时延神经网络 (TDNNs) 有关，这是由 [35] 在 1990 年代初期引入的。TDNN 在输入中应用时间卷积层次结构，但不使用池化、跳过连接、更新的激活（例如，整流线性单元）或我们 TCN 的其他功能。

3. Temporal Convolutional Networks

在本节中，我们定义了两个 TCN，每个都具有以下属性：（1）计算是逐层执行的，这意味着每个时间步同时更新，而不是每帧顺序更新（2）卷积是跨时间计算的，(3) 每帧的预测是固定长度时间段的函数，该时间段称为感受野（receptive field）。我们的 ED-TCN 使用具有时间卷积的编码器-解码器架构，而从 WaveNet 模型改编的膨胀 TCN 使用一系列深度膨胀卷积。

对于给定视频的每一帧，TCN 的输入将是一组视频特征，例如来自空间或时空 CNN 的输出。令 Xt ∈ RF0 为时间步长为 F0 的输入特征向量，时间步长为 1 ≤ t ≤ T。请注意，每个视频序列的时间步长 T 可能会有所不同。每帧的动作标签由向量 Y t ∈ { 0 , 1 } C Y_t ∈ \{0, 1\}^C Yt​∈{0,1}C 给出，其中 C 是类的数量，使得真正的类为 1，其他所有类为 0。

3.1. Encoder-Decoder TCN

我们的编码器-解码器框架如图 1 所示。编码器由 L 层组成，由 E(l) ∈ RFl×Tl 表示，其中 Fl 是第 l 层中卷积滤波器的数量，Tl 是相应时间步长的数量。每层由时间卷积、非线性激活函数和跨时间的最大池化组成。

我们将每一层中的滤波器集合定义为 W = { W ( i ) } i = 1 F l W = \{W^{(i)}\}^{F_l}_{i=1} W={W(i)}i=1Fl​​ 对于 $W^{(i)}\in {\mathbb{R}}^{d\times F_{l-1}}$ 和相应的偏置向量 $b\in R^{F_l}$。给定来自前一层的信号 $E^{(l-1)}$，我们计算激活 $E^{(l)}$

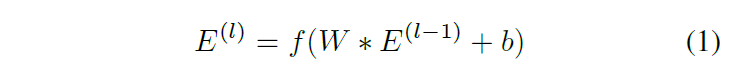
其中 $f(\cdot )$ 是激活函数，$\ast$ 是卷积算子。我们比较了第 4.4 节中的激活函数，发现归一化的整流线性单元（ReLU）表现最好。在每个激活函数之后，我们在时间上应用宽度为 2 的最大池化，使得 $T_l=1/2T_{l-1}$。池化使我们能够有效地计算长时间窗口上的激活。

我们的解码器与编码器类似，不同之处在于使用上采样而不是池化，并且操作的顺序现在是上采样、卷积和应用激活函数。通过简单地重复每个条目两次来执行上采样。解码器中的卷积滤波器将激活从中间的压缩层分配到顶部的动作预测。实验中，这些卷积大大提高了性能，并且似乎捕获了动作之间的成对转换。每个解码器层用 D(l) ∈ RFl×Tl 表示，其中 l ∈ {L, . . . , 1}。请注意，与编码器相比，它们的索引顺序相反，因此第一个编码器层中的滤波器计数与最后一个解码器层中的滤波器计数相同。

帧 t 对应于 C 个动作中的每个类别的概率由向量 ${\hat{Y}}_t\in [0,1{]}^C$ 使用权重矩阵 $U\in R^{C\times F_1}$ 和偏置 $c\in {\mathbb{R}}^C$ 给出，使得

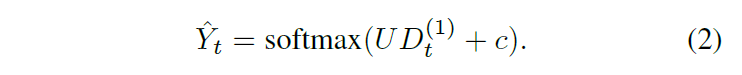
我们探索了其他机制，例如层之间的跳过连接、不同的卷积模式和其他归一化方案，但是，所提出的模型优于这些替代方案，并且可以说更简单。实施细节在第 3.3 节中描述。

感受野（Receptive Field）：每帧的预测是固定长度时间段的函数，由 $L$ 层和持续时间 $d$ 的公式 $r(d,L)=d(2^L-1)+1$ 给出。

3.2. Dilated TCN

我们将专为语音合成设计的 WaveNet [33] 模型应用于动作分割任务。在他们的工作中，预测输出 Yt 表示在给定第 1 帧到第 t 帧的音频的情况下，接下来应该出现哪个音频样本。在我们的例子中，Yt 是给定视频特征到 t 的当前动作。

如图 2 所示，我们定义了一系列块，每个块包含一系列 L 个卷积层。第 l 层和第 j 个块中的激活由 S(j,l) ∈ RFw×T 给出。请注意，每一层都有相同数量的滤波器 Fw。这使我们能够在以后组合来自不同层的激活。每层由一组具有速率参数 s 的膨胀卷积、一个非线性激活 f(·) 和一个残差连接组成，该连接将层的输入和卷积信号组合在一起。卷积只应用于两个时间步长，t 和 t - s，所以我们写出完整的方程是具体的。滤波器由 W = {W (1), W (2)} 参数化，其中 W (i) ∈ RFw×Fw 和偏置向量 b ∈ RFw。设 ^S(j,l) t 是时间 t 的膨胀卷积的结果，S(j,l) t 是添加残差连接后的结果，使得

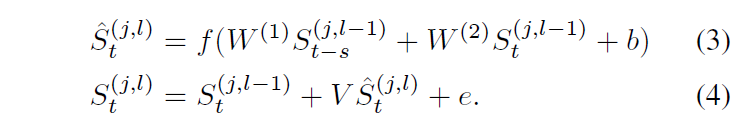
设 V ∈ RFw×Fw 和 e ∈ RFw 是残差的一组权重和偏差。请注意，参数 {W, b, V, e} 对于每一层都是独立的。

块内连续层的膨胀率增加，使得 $s_l=2^l$。这使我们能够在不大幅增加参数数量的情况下大幅增加感受野。

感受野：每个 Dilated TCN 层中的滤波器都小于 ED-TCN 中的滤波器，因此为了获得相同大小的感受野，它需要更多的层或块。对于块数 $B$ 和每个块的层数 $L$，其感受野的表达式为 $r(B,L)=B\ast 2^L$。

3.3. Implementation details

使用随机梯度下降和 ADAM [12] 步骤更新的分类交叉熵损失来学习两个 TCN 的参数。在全卷积滤波器 [31] 上使用 dropout，而不是单独的权重，可以提高性能并产生更平滑的权重。对于 ED-TCN，L 层中的每一层都有 $F_l=96+32\ast l$ 个滤波器。对于 Dilated TCN，我们发现性能在很大程度上取决于每个卷积层的滤波器数量，因此我们设置 Fw = 128。我们在实验中对不同的层数和滤波器持续时间进行消融分析。所有模型均使用 Keras [4] 和 TensorFlow [1] 实现。

3.4. Causal versus Acausal

我们进行因果和非因果实验。因果意味着时间 t 的预测只是时间 1 到 t 数据的函数，这对于机器人技术的应用很重要。非因果意味着预测可能是序列中任何时间步长的数据的函数。对于 ED-TCN 中的因果情况，对于每个时间步 t 和滤波器长度 d，我们从 Xt−d 卷积到 Xt。在非因果情况下，我们从 Xt- d/2 卷积到 Xt+ d/2 。

对于非因果膨胀 TCN，我们修改 Eqn 3，使得每一层现在都在前一个步骤、当前步骤和一个未来步骤上运行：

4. Evaluation & Discussion

我们首先进行合成实验，突出我们的 TCN 捕获高级时间模式的能力。然后，我们对三个具有挑战性的数据集和消融分析进行定量实验，以测量超参数的影响，例如过滤持续时间。

4.1. Metrics

处理动作分割的 apers 倾向于使用与动作检测不同的指标。我们使用来自两个社区的指标进行评估，并引入适用于这两个任务的分段 F1 分数。

分割指标：动作分割论文倾向于使用逐帧指标，例如准确率、精度和召回率 [29, 13]。一些关于 50 Salads 的工作还使用分段度量 [15, 16]，以分段编辑距离的形式，这很有用，因为它会惩罚无序和过度分段错误的预测。我们使用逐帧精度评估所有方法。

逐帧度量的一个缺点是，达到相似精度的模型可能会有很大的定性差异，正如稍后可视化的那样。例如，一个模型可以实现高精度，但会产生大量的过度分割错误。避免这些错误对于人机交互和视频摘要很重要。

检测指标：动作检测论文倾向于使用分段指标，例如具有中点命中标准 (midpoint hit criterion，mAP@mid) [25, 27] 的平均精度（mAP） 或 具有联合交叉 (IoU) 重叠标准 (mAP@k) 的 mAP [ 24]。 mAP@k 是通过比较每个段的重叠分数与同一类的真实动作标签来计算的。如果 IoU 分数高于阈值 τ = k/100，则视为真阳性，否则为假阳性。计算每个类的平均精度，并对结果进行平均。 mAP@mid 类似，除了真阳性的标准是中点（平均时间）是否在相应正确动作的开始和停止时间内。

mAP 是视频搜索等信息检索任务的有用指标，但是对于许多细粒度的动作检测应用程序，例如机器人或视频监控，我们发现结果并不代表真实世界的性能。关键问题是mAP对分配给每个段预测的置信度分数非常敏感。这些置信度通常只是对应于预测片段的帧内的平均或最大类别分数。通过以微妙不同的方式计算这些置信度，您可以获得截然不同的结果。在 MERL 购物中，Singh 等人 [27] 的 mAP@mid 得分，使用区间内的平均预测分数从 50.9 跃升至使用同一区间内的最高分数的 69.8。

F1@k：我们提出了一个分段 F1 分数，它适用于分割和检测任务，具有以下特性：（1）它惩罚过度分割错误，（2）它不惩罚预测之间的微小时间变化和真实标签，这可能是由注释器的可变性引起的，以及 (3) 分数取决于动作的数量，而不是每个动作实例的持续时间。该指标类似于具有 IoU 阈值的 mAP，只是它不需要每个预测的置信度。定性地，我们发现这些数字更能表明给定分割的口径。

我们通过使用阈值 τ 将其 IoU 与相应的基本事实进行比较来计算每个预测的动作片段是真还是假阳性。与 mAP 检测分数一样，如果在单个真实动作的跨度内有多个正确检测，则只有一个被标记为真阳性，所有其他都是假阳性。我们计算所有类别的真阳性、假阳性和假阴性的精度和召回率，并计算 F1 = 2 (prec∗recall) / (prec+recall)。

4.2. Synthetic Experiments

我们声称 TCN 能够捕获复杂的时间模式，例如动作组合、动作持续时间和长期时间依赖性。我们通过两个综合实验展示了这些能力。对于每一个，我们为 50 个训练序列和 10 个长度为 T = 150 的测试序列生成玩具特征 X 和相应的标签 Y。给定类的每个动作的持续时间是固定的，并且动作片段是随机采样的。图 3 显示了组合实验的一个示例。两个 TCN 都是非因果的，并且具有长度为 16 的感受野。

动作组合（Action Compositions）：根据定义，一个活动由一系列动作组成。通常，连续动作之间存在依赖关系（例如，动作 B 可能在 A 之后）。 CRF 使用类标签上的成对转换模型捕获这一点，而 RNN 使用 LSTM 跨潜在状态捕获它。我们表明，TCN 可以捕获动作组合，尽管没有在该层中的先前时间步上明确调节时间 t 的激活。

在本实验中，我们使用带有三个高级动作 A、B 和 C 以及子动作 A1、A2 和 A3 的马尔可夫模型生成序列，如图 3 所示。A 始终由子动作 A1（深蓝色）、A2 组成（浅蓝色），然后是 A3（绿色），然后过渡到 B 或 C。为简单起见，Xt ∈ R3 对应于高级动作 Yt，使得真实类别为 +1，其他类别为 -1。

对应于子动作 A1-A3 的特征向量都是相同的，因此一个简单的基于帧的分类器将无法区分它们。鉴于 TCN 的长接收域，它们可以完美地分割动作。这表明我们的 TCN 能够捕获动作组合。回想一下，每个动作类都有不同的片段持续时间，我们正确标记了所有帧，这表明 TCN 可以捕获每个类的持续时间属性。

长期时间依赖性（Long-range temporal dependencies）：对于许多操作，重要的是要考虑过去几秒钟甚至几分钟的信息。例如，在烹饪场景中，当用户切番茄时，他们往往用手遮挡番茄，这使得很难识别正在切的是哪个物体。在用户开始切割动作之前识别出番茄在砧板上是有利的。在这个实验中，我们展示了 TCN 能够通过向特征添加相位延迟来学习这些长程时间模式。具体来说，对于训练和测试特征，我们将 ˆX 定义为所有 t 的 ˆXt = Xt−s。因此，标签和相应的特征之间存在 s 帧的延迟。

使用 F1@10 的结果如 4.2 所示。为了比较，我们展示了 TCN 和 Bi-LSTM。正如预期的那样，所有模型都没有延迟（s = 0），实现了完美的预测。对于短延迟（s = 5），TCN 可以正确检测除序列的第一个和最后一个之外的所有动作。随着延迟的增加，ED-TCN 和 Dilated TCN 的表现非常好，最多可达感受野长度的一半。 Bi-LSTM 的结果以更快的速度下降。

4.3. Datasets

University of Dundee 50 Salads [29]：包含 50 个用户制作沙拉的序列，并已用于动作分割和检测。虽然这是一个多模式数据集，但我们仅使用视频数据进行评估。每个视频时长 5-10 分钟，包含大约 30 个动作实例，例如切番茄或剥黄瓜。我们在更高级别的动作粒度上执行了 5 次拆分的交叉验证，其中包括 9 个动作类，例如添加调味品、添加油、切割、混合成分、剥皮和放置，以及一个背景类。在 [29] 中，这被称为“评估”。我们还评估了具有 17 个动作类的中级动作粒度。中级标签区分了切番茄和切黄瓜之类的动作，而更高级别的标签将它们组合成一个类，cut。

我们使用 Lea 等人 [15] 的空间 CNN 特征作为我们模型的输入。这是一个简化的 VGG 风格模型，仅在 50 Salads上进行训练。数据被下采样到大约 1 帧/秒。

MERL Shopping [27]：是一个动作检测数据集，由 106 个监控式视频组成，用户在这些视频中与商店货架上的物品进行交互。摄像机视点是固定的，每个视频中只有一个用户。有五个动作加上一个背景类：到达货架，从货架上收回手，把手放在货架上，检查产品，检查货架。动作通常持续几秒钟。

我们使用 Singh 等人 [27] 的特征作为输入。 Singh 的模型由四个 VGG 风格的空间 CNN 组成：一个用于 RGB，一个用于光流，一个用于 RGB 和光流的裁剪版本。我们为每一帧堆叠四种特征类型，并使用具有 50 个分量的主成分分析来降低维度。训练、验证和测试拆分与 [27] 中描述的相同。数据以 2.5 帧/秒的速度采样。

Georgia Tech Egocentric Activities (GTEA) [8]：包含 28 个视频，包含 7 种厨房活动，例如制作三明治和煮咖啡。四名受试者每项活动执行一次。摄像头安装在用户的头上并指向他们的手。平均而言，每个视频大约有 19 个（非背景）动作，视频时长约为一分钟。我们使用 [6] 中定义的 11 个动作类，并使用留下一个用户进行评估。如 [28] 所做的那样，对用户 1-3 执行交叉验证。我们使用每秒 3 帧的帧速率。

我们无法从 [28] 中获得最先进的特征，因此我们使用 [15] 中的代码从头开始训练空间 CNN，该代码最初应用于 50 份沙拉。这是一个简化的 VGG 风格的网络，其中每一帧的输入是一对 RGB 和运动图像。由于该数据集中的大量视频压缩，光流非常嘈杂，因此我们简单地使用差异图像，这样对于第 t 帧的图像 It，运动图像是 [It−d − It, It+d − It , It−2d − It, It+2d − It] 延迟 d = 0.5 秒。这些差异图像可以看作是一种简单的注意力机制。我们比较了这个空间 CNN、[15] 的时空 CNN、EgoNet [28] 和我们的 TCN 的结果。

4.4. Experimental Results

为了使基线更具竞争力，我们将双向 LSTM (Bi-LSTM) [5] 应用于 50 Salads 和 GTEA。我们在每个 LSTM 方向使用 64 个潜在状态，具有与前面描述的相同的损失和学习方法。该模型的输入与 TCN 相同。请注意，MERL Shopping 已经有了这个基线。

50 Salads：两种操作粒度的结果都包含在表 4.4 中。所有方法都以非因果模式进行评估。 ED-TCN 在粒度和所有指标上都优于所有其他模型。我们还与 Richard 等人进行了比较。 [24] 在中级进行评估并使用 IoU mAP 检测指标进行了报告。他们的方法达到了 37.9 mAP@10 和 22.9 mAP@50。 ED-TCN 达到 64.9 mAP@10 和 42.3 mAP@50，膨胀 TCN 达到 53.3 mAP@10 和 29.2 mAP@50。

请注意，ED-TCN、Dilated TCN 和 ST-CNN 都实现了相似的逐帧精度，但 F1@k 和编辑分数却大不相同。与竞争方法相比，ED-TCN 倾向于产生更少的过度分割。图 5 显示了这些模型的中级预测。包括每个预测的准确性和 F1 以进行比较。

该数据集上的许多错误是由于动作之间的极端相似性和对象外观的细微差异造成的。例如，我们的模型使用外观相似的醋瓶和橄榄油瓶来混淆动作。同样，我们混淆了一些切割动作（例如，切黄瓜与切番茄）和放置动作（例如，放置奶酪与放置生菜）。

MERL Shopping：我们使用 Singh 等人的两组预测进行比较。 [27]，如表 4.4 所示。第一个，如他们的论文中所报道的，是一组稀疏的动作检测，称为 MSN Det。第二个是从作者那里获得的，是一组密集的（每帧）动作分割。检测使用来自密集分段的激活和非最大抑制检测算法来输出一组稀疏分段。他们的因果版本在密集激活上使用 LSTM，而他们的非因果版本使用双向 LSTM。

虽然 Singh 的检测实现了非常高的中点 mAP，但相同的预测在其他指标上的表现非常差。如图 5（右）所示，动作非常短且稀疏。这在优化中点 mAP 时是有利的，因为性能仅取决于给定操作的中点，但是，如果您需要活动的开始和停止时间，则它无效。有趣的是，这种方法在 F1 中表现最差，即使对于低重叠也是如此。

正如预期的那样，非因果 TCN 的表现要好于因果变体。这验证了使用未来信息对于实现最佳性能很重要。在因果和非因果结果中，Dilated TCN 在中点 mAP 中的表现优于 ED-TCN，但是，ED-TCN 的 F1 分数更好。这表明膨胀 TCN 的置信度比 ED-TCN 更可靠。

Georgia Tech Egocentric Activities：ED-TCN 的性能与 Singh 等人的集成方法相当。 [28]，它将 EgoNet 特征与 TDD [17] 相结合。回想一下，Singh 的方法不包含时间模型，因此我们希望将它们的特征与我们的 ED-TCN 结合起来可以提高性能。与 EgoNet 和 TDD 不同，我们的方法使用可以实时计算的更简单的空间 CNN 特征。

总体而言，在我们的实验中，Encoder-Decoder TCN 优于所有其他模型，包括大多数数据集的最先进方法以及我们对最近 WaveNet 模型的适应。这些模型之间最重要的区别是 ED-TCN 使用更少的层但具有更长的卷积滤波器，而 Dilated TCN 具有更多的层但具有更短的滤波器。 ED-TCN 中的长滤波器对 F1 性能有很大的积极影响，特别是因为它们可以防止过度分割问题。 Dilated TCN 在准确度等指标上表现良好，但对过度分割的鲁棒性较差。这可能是由于每层中的滤波器长度较短。

4.4.1 Ablative Experiments

对 50 Salads（中级）进行了消融实验。请注意，这些是使用不同的超参数完成的，因此可能与以前的结果不匹配。

激活函数：我们使用表 4.4.1 中显示的激活函数来评估性能。门控 PixelCNN (GPC) 激活 [34]，f(x) = tanh(x) ○ sigmoid(x) 用于 WaveNet，并且在我们的任务中也实现了高性能。我们定义了归一化 ReLU：

感受野（Receptive fields）：我们将性能与不同的感受野超参数进行比较。图 4（左）中的线显示了 ED-TCN 上 L 从 1 到 5 和滤波器尺寸 d 从 1 到 40 的 F1@25。图 4（右）中的线对应于膨胀 TCN 的块计数 B，层数 L 从 1 到 6。请注意，我们的 GPU 在 (L = 4,d = 25) 和 Dilated TCN (B = 4,L = 5) 之后的 ED-TCN 上内存不足。 ED-TCN 在 44 帧 (L = 2,d = 15) 的感受野中表现最佳，对应于 52 秒。 Dilated TCN 在 128 帧 (B = 4,L = 5) 时表现最佳，在 96 帧 (B = 3,L = 5) 时表现相似。

训练时间：训练 TCN 比 Bi-LSTM 花费的时间要少得多。虽然确切的时间因 TCN 层数和滤波器长度而异，但对于 50 个沙拉的分割 - 使用 Nvidia Titan X 进行 200 个 epoch - 训练 ED-TCN 大约需要一分钟，而训练 Bi 大约需要 30 分钟-LSTM。这种加速源于每个 TCN 层内的激活都是独立的，因此它们可以在 GPU 上批量执行。中间 RNN 层中的激活取决于该层中先前的激活，因此必须按顺序应用操作。

5. Conclusion

我们介绍了时间卷积网络，它使用卷积层次来捕获远程时间模式。我们在合成数据上表明，TCN 能够捕获复杂的模式，例如成分、动作持续时间，并且对时间延迟具有鲁棒性。我们的模型优于强大的基线，包括双向 LSTM，并在具有挑战性的数据集上实现了最先进的性能。我们相信 TCN 是 RNN 的强大替代品，值得进一步探索。