热门标签
热门文章
- 1deepin安装bochs2.6.2_2.kafka安装与使用
- 2GitHub上的项目受美国出口管制吗？
- 3Codeforces Round #700 (Div. 2)A-D2题解_怪物的初始生命值为 m,每次攻击对怪物以 均等的 1/(m + 1) 的概率
- 4OpenCV-Python 图像平滑处理2：blur函数及滤波案例
- 5执行sudo apt-get upgrade时报错 dpkg: error processing package xxxxxx_package libsensors5:amd64 is not configured yet
- 6使用OpenFeign实现服务远程调用_openfeign远程调用案例
- 7codeforces的polygon平台使用指北_codeforces polygon
- 8Python多进程多线程测试_with threadpoolexecutor(max_workers=4) as executor
- 9使用flask将Yolov5部署到前端页面实现视频检测（保姆级）_yolov5(pytorch)目标检测实战:flask web部署
- 10Tim Yang：后端技术这一年_timyang filter
当前位置: article > 正文
直方图均衡化—C++代码实现_自适应直方图均衡化代码实现
作者：Monodyee | 2024-02-12 22:26:28
赞
踩
自适应直方图均衡化代码实现
在医疗图像检测领域，为了能够使得采集到效果较好的X光或超声图像，会经常需要进行图像增强，如下图所示。图像增强的方法有很多，本文主要针对直方图均衡化相关的方法进行C++实现。共分为以下几个部分：
- 1 直方图均衡化（HE）
- 2 自适应直方图均衡化（AHE）
- 3 限制对比度的自适应直方图均衡化
- 4 局部直方图统计量
直方图均衡化（HE）
直方图均衡化（histogram equlization）的主要思想是将一副图像的直方图分布变成近似均匀分布，从而增强图像的对比度。直方图均衡化虽然只是数字图像处理(Digital Image Processing)里面的基本方法，但是其作用很强大，是一种很经典的算法。
关于直方图均衡化原理介绍可以看这篇文章
代码如下：
//HE(直方图均衡化) bool HE_MY(Mat gray, Mat result) { //统计0~255像素值的个数 map<int, int>mp; for (int i = 0; i < gray.rows; i++) { uchar* ptr = gray.data + i * gray.cols; for (int j = 0; j < gray.cols; j++) { int value = ptr[j]; mp[value]++; } } //统计0~255像素值的频率，并计算累计频率 map<int, double> valuePro; int sum = gray.cols * gray.rows; double sumPro = 0; for (int i = 0; i < 256; i++) { sumPro += 1.0 * mp[i] / sum; valuePro[i] = sumPro; } //根据累计频率进行转换 for (int i = 0; i < gray.rows; i++) { uchar* ptr1 = gray.data + i * gray.cols; for (int j = 0; j < gray.cols; j++) { int value = ptr1[j]; double p = valuePro[value]; result.at<uchar>(i, j) = p * 255; } } return true; }
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
自适应直方图均衡化（AHE）
自适应直方图均衡化（adaptive histogram equalization）其实是将图像切分为许多不同的区域, 对每个区域分别进行直方图均衡化，即局部直方图均衡化。通常会产生块状的效果，需要对其进行插值运算，使得块状区域之间过度较为自然。常用的插值算法有：最邻近插值、线性插值、双线性插值、双三次插值，opencv中的 resize() 函数就是使用的双线性插值的方法。具体介绍可以参考这篇文章：图像处理之-----插值算法
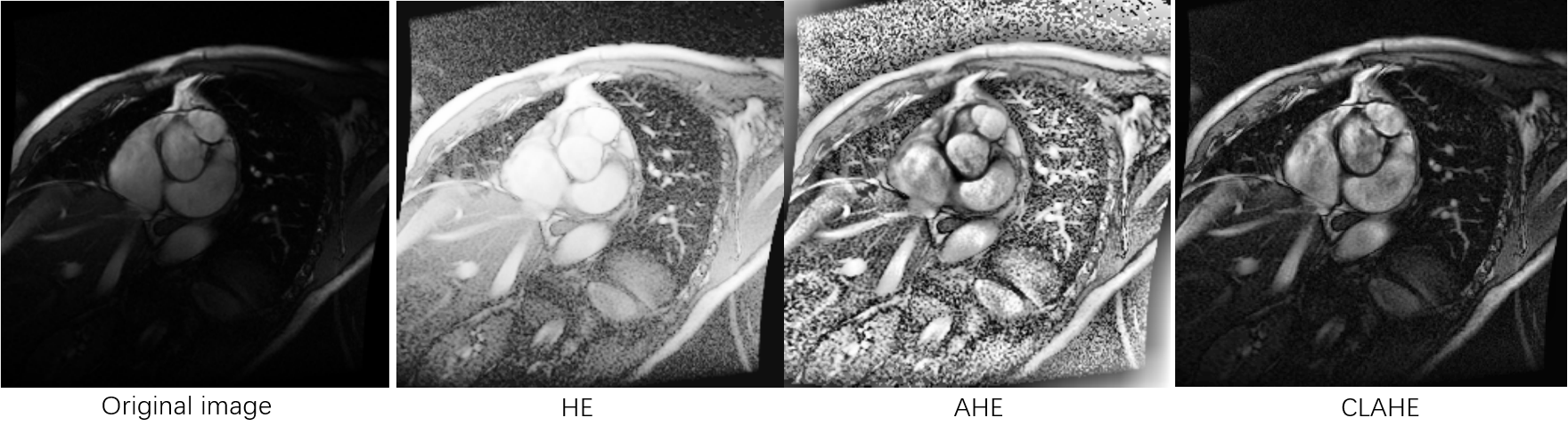
几种对比度拉伸算法的效果对比如下图所示。原图的阴影区域中存在一些对比度不明显的字符，使用全局拉伸的直方图均衡化后，阴影区域中的字符对比度拉伸强度较小，而且白色区域的一些噪声被放大了。使用AHE拉伸后，阴影区域的字符对比度明显，但对比度拉伸范围过大，使得阴影区域的亮度提高了很多，且放大了很多噪声点。使用CLAHE算法则能够得到较好的效果，将在下面进行介绍。
AHE（插值）算法代码如下：
Mat AHE(Mat originImage, int blockNumber = 16) { Mat src = originImage.clone(); Mat src1 = originImage.clone(); Mat dst; //const int blockNumber = 8;//把图像分成block数量 int width = src.cols; int height = src.rows; int singleBlockWidth = src.cols / blockNumber;//每个block大小 int singleBlockHeight = src.rows / blockNumber; int (*pixelNumber)[256] = new int[blockNumber * blockNumber][256]{ 0 };//存储不同block中各个不同灰度像素数量 float (*total)[256] = new float[blockNumber * blockNumber][256]{ 0.0 };//累积分布函数 for (int i = 0; i < blockNumber; i++) { for (int j = 0; j < blockNumber; j++) { int startPixelW = (i)*singleBlockWidth; int endPixelW = (i + 1) * singleBlockWidth; int startPixelH = (j)*singleBlockHeight; int endPixelH = (j + 1) * singleBlockHeight; int number = i + blockNumber * j;//统计运算到哪一个block了 int singleBlockPixelNumber = singleBlockWidth * singleBlockHeight; for (int x = startPixelW; x < endPixelW; x++)//统计不同block中各个不同灰度像素数量 for (int y = startPixelH; y < endPixelH; y++) { int pixelValue = src.at<uchar>(y, x); pixelNumber[number][pixelValue]++; } for (int k = 0; k < 256; k++)//计算累积分布函数 { if (k == 0) total[number][k] = 1.0 * pixelNumber[number][k] / singleBlockPixelNumber; else total[number][k] = total[number][k - 1] + 1.0 * pixelNumber[number][k] / singleBlockPixelNumber; } } } //利用累积分布函数对于原像素灰度在各自block中进行映射 for (int i = 0; i < blockNumber; i++) { for (int j = 0; j < blockNumber; j++) { int startPixelW = (i)*singleBlockWidth; int endPixelW = (i + 1) * singleBlockWidth; int startPixelH = (j)*singleBlockHeight; int endPixelH = (j + 1) * singleBlockHeight; int number = i + blockNumber * j; int singleBlockPixelNumber = singleBlockWidth * singleBlockHeight; for (int x = startPixelW; x < endPixelW; x++) for (int y = startPixelH; y < endPixelH; y++) { int pixelValue = src1.at<uchar>(y, x); src1.at<uchar>(y, x) = total[number][pixelValue] * 255; } } } //插值 for (int i = 0; i < width; i++) { for (int j = 0; j < height; j++) { //four coners if (i <= singleBlockWidth / 2 && j <= singleBlockHeight / 2) { int num = 0; src.at<uchar>(j, i) = (int)(total[num][src.at<uchar>(j, i)] * 255); } else if (i <= singleBlockWidth / 2 && (j >= ((blockNumber - 1) * singleBlockHeight + singleBlockHeight / 2))) { int num = blockNumber * (blockNumber - 1); src.at<uchar>(j, i) = (int)(total[num][src.at<uchar>(j, i)] * 255); } else if (i >= ((blockNumber - 1) * singleBlockWidth + singleBlockWidth / 2) && j <= singleBlockHeight / 2) { int num = blockNumber - 1; src.at<uchar>(j, i) = (int)(total[num][src.at<uchar>(j, i)] * 255); } else if (i >= ((blockNumber - 1) * singleBlockWidth + singleBlockWidth / 2) && j >= ((blockNumber - 1) * singleBlockHeight + singleBlockHeight / 2)) { int num = blockNumber * blockNumber - 1; src.at<uchar>(j, i) = (int)(total[num][src.at<uchar>(j, i)] * 255); } //four edges except coners else if (i <= singleBlockWidth / 2){ //线性插值 int num_i = 0; int num_j = (j - singleBlockHeight / 2) / singleBlockHeight; int num1 = num_j * blockNumber + num_i; int num2 = num1 + blockNumber; float p = (j - (num_j * singleBlockHeight + singleBlockHeight / 2)) / (1.0f * singleBlockHeight); float q = 1 - p; src.at<uchar>(j, i) = (int)((q * total[num1][src.at<uchar>(j, i)] + p * total[num2][src.at<uchar>(j, i)]) * 255); } else if (i >= ((blockNumber - 1) * singleBlockWidth + singleBlockWidth / 2)) { //线性插值 int num_i = blockNumber - 1; int num_j = (j - singleBlockHeight / 2) / singleBlockHeight; int num1 = num_j * blockNumber + num_i; int num2 = num1 + blockNumber; float p = (j - (num_j * singleBlockHeight + singleBlockHeight / 2)) / (1.0f * singleBlockHeight); float q = 1 - p; src.at<uchar>(j, i) = (int)((q * total[num1][src.at<uchar>(j, i)] + p * total[num2][src.at<uchar>(j, i)]) * 255); } else if (j <= singleBlockHeight / 2) { //线性插值 int num_i = (i - singleBlockWidth / 2) / singleBlockWidth; int num_j = 0; int num1 = num_j * blockNumber + num_i; int num2 = num1 + 1; float p = (i - (num_i * singleBlockWidth + singleBlockWidth / 2)) / (1.0f * singleBlockWidth); float q = 1 - p; src.at<uchar>(j, i) = (int)((q * total[num1][src.at<uchar>(j, i)] + p * total[num2][src.at<uchar>(j, i)]) * 255); } else if (j >= ((blockNumber - 1) * singleBlockHeight + singleBlockHeight / 2)) { //线性插值 int num_i = (i - singleBlockWidth / 2) / singleBlockWidth; int num_j = blockNumber - 1; int num1 = num_j * blockNumber + num_i; int num2 = num1 + 1; float p = (i - (num_i * singleBlockWidth + singleBlockWidth / 2)) / (1.0f * singleBlockWidth); float q = 1 - p; src.at<uchar>(j, i) = (int)((q * total[num1][src.at<uchar>(j, i)] + p * total[num2][src.at<uchar>(j, i)]) * 255); } //双线性插值 else { int num_i = (i - singleBlockWidth / 2) / singleBlockWidth; int num_j = (j - singleBlockHeight / 2) / singleBlockHeight; int num1 = num_j * blockNumber + num_i; int num2 = num1 + 1; int num3 = num1 + blockNumber; int num4 = num2 + blockNumber; float u = (i - (num_i * singleBlockWidth + singleBlockWidth / 2)) / (1.0f * singleBlockWidth); float v = (j - (num_j * singleBlockHeight + singleBlockHeight / 2)) / (1.0f * singleBlockHeight); src.at<uchar>(j, i) = (int)((u * v * total[num4][src.at<uchar>(j, i)] + (1 - v) * (1 - u) * total[num1][src.at<uchar>(j, i)] + u * (1 - v) * total[num2][src.at<uchar>(j, i)] + v * (1 - u) * total[num3][src.at<uchar>(j, i)]) * 255); } } } return src; }
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
- 43
- 44
- 45
- 46
- 47
- 48
- 49
- 50
- 51
- 52
- 53
- 54
- 55
- 56
- 57
- 58
- 59
- 60
- 61
- 62
- 63
- 64
- 65
- 66
- 67
- 68
- 69
- 70
- 71
- 72
- 73
- 74
- 75
- 76
- 77
- 78
- 79
- 80
- 81
- 82
- 83
- 84
- 85
- 86
- 87
- 88
- 89
- 90
- 91
- 92
- 93
- 94
- 95
- 96
- 97
- 98
- 99
- 100
- 101
- 102
- 103
- 104
- 105
- 106
- 107
- 108
- 109
- 110
- 111
- 112
- 113
- 114
- 115
- 116
- 117
- 118
- 119
- 120
- 121
- 122
- 123
- 124
- 125
- 126
- 127
- 128
- 129
- 130
- 131
- 132
- 133
- 134
- 135
- 136
- 137
- 138
- 139
- 140
- 141
- 142
- 143
- 144
- 145
- 146
限制对比度的自适应直方图均衡化（CLAHE）
CLAHE是1993年提出的方法，通过对局部直方图均衡化的对比度进行限制，从而避免所有局部区域的像素灰度值都映射到（0-255）的范围内，能够较好地保持原图的自然度，同时也能起到抑制噪声的作用。
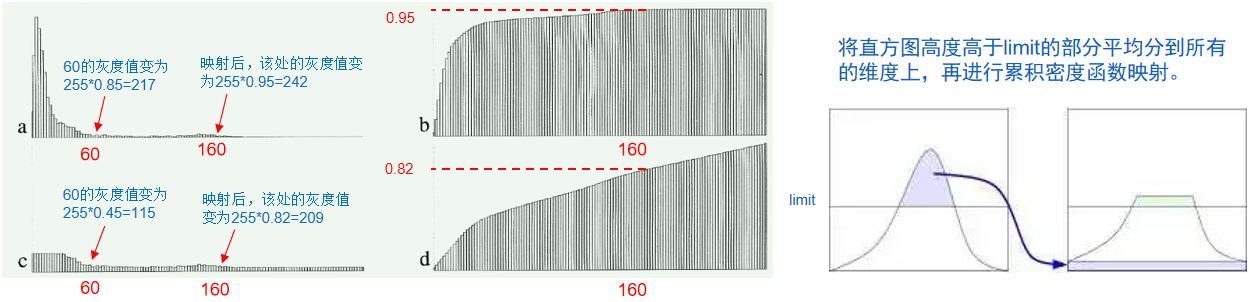
上图a代表原图的直方图，b是其累积概率密度函数；c和d则为进行对比度限制后的直方图和累积概率分布函数。对比度限制原理如上图右部分所示，通过设置一个阈值（通常情况下该值表示为图像像素个数的百分比），将像素数较多的区域切除掉，平均分配到所有其他的灰度值区域。未使用限制对比度时，原图中灰度值为60的像素映射后变为217，灰度值为160的像素映射后变为242，限制对比度后，则分别变为了115和209。可见能够起到限制对比度拉伸和抑制噪声的作用。
具体细节部分可以参考原论文：Contrast Limited Adaptive Histogram Equalization
作者为什么可以有这种灵感我们不得而知，但对于这种局部对比度限制的方法博主也在许多其他论文中看到过，我认为应该没有比较科学的解释，只是因为这种方法确实能够限制对比度的拉伸，且得到的效果也挺不错的。
几种不同的图像增强效果如下：
CLAHE代码如下：
//CLAHE Mat CLAHE_MY(Mat src, int block = 8, int limit = 4) { Mat CLAHE_GO = src.clone(); int width = src.cols; int height = src.rows; int width_block = width / block; //每个小格子的长和宽 int height_block = height / block; //存储各个直方图 int(*tmp2)[256] = new int[block * block][256]{ 0 }; float(*C2)[256] = new float[block * block][256]{ 0.0 }; //分块 int total = width_block * height_block; for (int i = 0; i < block; i++) { for (int j = 0; j < block; j++) { int start_x = i * width_block; int end_x = start_x + width_block; int start_y = j * height_block; int end_y = start_y + height_block; int num = i + block * j; //遍历小块,计算直方图 for (int ii = start_x; ii < end_x; ii++) { for (int jj = start_y; jj < end_y; jj++) { int index = src.at<uchar>(jj, ii); tmp2[num][index]++; } } //裁剪和增加操作 int LIMIT = limit * width_block * height_block / 255; int steal = 0; for (int k = 0; k < 256; k++) { if (tmp2[num][k] > LIMIT) { steal += tmp2[num][k] - LIMIT; tmp2[num][k] = LIMIT; } } int bonus = steal / 256; //hand out the steals averagely for (int k = 0; k < 256; k++) { tmp2[num][k] += bonus; } //计算累积分布直方图 for (int k = 0; k < 256; k++) { if (k == 0) C2[num][k] = 1.0f * tmp2[num][k] / total; else C2[num][k] = C2[num][k - 1] + 1.0f * tmp2[num][k] / total; } } } //计算变换后的像素值 //根据像素点的位置，选择不同的计算方法 for (int i = 0; i < width; i++) { for (int j = 0; j < height; j++) { //four coners if (i <= width_block / 2 && j <= height_block / 2) { int num = 0; CLAHE_GO.at<uchar>(j, i) = (int)(C2[num][CLAHE_GO.at<uchar>(j, i)] * 255); } else if (i <= width_block / 2 && j >= ((block - 1) * height_block + height_block / 2)) { int num = block * (block - 1); CLAHE_GO.at<uchar>(j, i) = (int)(C2[num][CLAHE_GO.at<uchar>(j, i)] * 255); } else if (i >= ((block - 1) * width_block + width_block / 2) && j <= height_block / 2) { int num = block - 1; CLAHE_GO.at<uchar>(j, i) = (int)(C2[num][CLAHE_GO.at<uchar>(j, i)] * 255); } else if (i >= ((block - 1) * width_block + width_block / 2) && j >= ((block - 1) * height_block + height_block / 2)) { int num = block * block - 1; CLAHE_GO.at<uchar>(j, i) = (int)(C2[num][CLAHE_GO.at<uchar>(j, i)] * 255); } //four edges except coners else if (i <= width_block / 2) { //线性插值 int num_i = 0; int num_j = (j - height_block / 2) / height_block; int num1 = num_j * block + num_i; int num2 = num1 + block; float p = (j - (num_j * height_block + height_block / 2)) / (1.0f * height_block); float q = 1 - p; CLAHE_GO.at<uchar>(j, i) = (int)((q * C2[num1][CLAHE_GO.at<uchar>(j, i)] + p * C2[num2][CLAHE_GO.at<uchar>(j, i)]) * 255); } else if (i >= ((block - 1) * width_block + width_block / 2)) { //线性插值 int num_i = block - 1; int num_j = (j - height_block / 2) / height_block; int num1 = num_j * block + num_i; int num2 = num1 + block; float p = (j - (num_j * height_block + height_block / 2)) / (1.0f * height_block); float q = 1 - p; CLAHE_GO.at<uchar>(j, i) = (int)((q * C2[num1][CLAHE_GO.at<uchar>(j, i)] + p * C2[num2][CLAHE_GO.at<uchar>(j, i)]) * 255); } else if (j <= height_block / 2) { //线性插值 int num_i = (i - width_block / 2) / width_block; int num_j = 0; int num1 = num_j * block + num_i; int num2 = num1 + 1; float p = (i - (num_i * width_block + width_block / 2)) / (1.0f * width_block); float q = 1 - p; CLAHE_GO.at<uchar>(j, i) = (int)((q * C2[num1][CLAHE_GO.at<uchar>(j, i)] + p * C2[num2][CLAHE_GO.at<uchar>(j, i)]) * 255); } else if (j >= ((block - 1) * height_block + height_block / 2)) { //线性插值 int num_i = (i - width_block / 2) / width_block; int num_j = block - 1; int num1 = num_j * block + num_i; int num2 = num1 + 1; float p = (i - (num_i * width_block + width_block / 2)) / (1.0f * width_block); float q = 1 - p; CLAHE_GO.at<uchar>(j, i) = (int)((q * C2[num1][CLAHE_GO.at<uchar>(j, i)] + p * C2[num2][CLAHE_GO.at<uchar>(j, i)]) * 255); } //双线性插值 else { int num_i = (i - width_block / 2) / width_block; int num_j = (j - height_block / 2) / height_block; int num1 = num_j * block + num_i; int num2 = num1 + 1; int num3 = num1 + block; int num4 = num2 + block; float u = (i - (num_i * width_block + width_block / 2)) / (1.0f * width_block); float v = (j - (num_j * height_block + height_block / 2)) / (1.0f * height_block); CLAHE_GO.at<uchar>(j, i) = (int)((u * v * C2[num4][src.at<uchar>(j, i)] + (1 - v) * (1 - u) * C2[num1][src.at<uchar>(j, i)] + u * (1 - v) * C2[num2][src.at<uchar>(j, i)] + v * (1 - u) * C2[num3][src.at<uchar>(j, i)]) * 255); } } } return CLAHE_GO; }
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
- 43
- 44
- 45
- 46
- 47
- 48
- 49
- 50
- 51
- 52
- 53
- 54
- 55
- 56
- 57
- 58
- 59
- 60
- 61
- 62
- 63
- 64
- 65
- 66
- 67
- 68
- 69
- 70
- 71
- 72
- 73
- 74
- 75
- 76
- 77
- 78
- 79
- 80
- 81
- 82
- 83
- 84
- 85
- 86
- 87
- 88
- 89
- 90
- 91
- 92
- 93
- 94
- 95
- 96
- 97
- 98
- 99
- 100
- 101
- 102
- 103
- 104
- 105
- 106
- 107
- 108
- 109
- 110
- 111
- 112
- 113
- 114
- 115
- 116
- 117
- 118
- 119
- 120
- 121
- 122
- 123
- 124
- 125
- 126
- 127
- 128
- 129
- 130
- 131
- 132
- 133
- 134
- 135
- 136
- 137
- 138
- 139
- 140
- 141
- 142
局部直方图统计量
局部直方图统计量的方法在冈萨雷斯的《数字图像处理》第四版中有介绍，比较简单好用，对于特定的场景往往能起到更好的效果。
代码如下：
//局部直方图统计量 /* 功能：对于图像中的每个像素点，截取其7*7的邻域框，计算邻域框的灰度均值mxy和方差deltaxy1，与整幅图像的邻域mean和方差delta1进行比较， if (mxy <= mean * k0 && deltaxy1 <= k2 * delta1 && deltaxy1 >= k1 * delta1){ 将该像素灰度值*10 }; */ double getMean(double* r_pdf) { double m = 0; for (int i = 0; i < 256; i++) m += i * r_pdf[i]; return m; } double getVariance(double* r_pdf, double m) { double delta = 0; for (int i = 0; i < 256; i++) if (r_pdf[i] != 0) delta += (pow((i - m), 2) * r_pdf[i]); return delta; } void init(double* r_pdf) { for (int i = 0; i < 256; i++) { r_pdf[i] = 0; } } int histStatistic(cv::Mat& src, int dim, float k0, float k1, float k2, float E) { if (dim % 2 == 0) { return -1; } int width = src.rows; int height = src.cols; int mn = width * height; double r_pdf[256] = {}; for (int row = 0; row < src.rows; row++) { for (int col = 0; col < src.cols; col++) { int g = src.at<uchar>(row, col); r_pdf[g] += 1.0 / mn; } } double mean = getMean(r_pdf); double delta = getVariance(r_pdf, mean); double delta1 = std::sqrt(delta); double mxy = 0; double deltaxy = 0; double local = dim * dim; for (int i = dim / 2; i < height - dim / 2 - 1; i++) { for (int j = dim / 2; j < width - dim / 2; j++) { init(r_pdf); //统计局部直方图 for (int p = j - dim / 2; p < j + dim / 2 + 1; p++) { for (int q = i - dim / 2; q < i + dim / 2 + 1; q++) { int g = src.at<uchar>(p, q); r_pdf[g] += 1.0 / local; } } mxy = getMean(r_pdf); deltaxy = getVariance(r_pdf, mxy); double deltaxy1 = sqrt(deltaxy); if (mxy <= mean * k0 && deltaxy1 <= k2 * delta1 && deltaxy1 >= k1 * delta1) { src.at<uchar>(j, i) = src.at<uchar>(j, i) * E; } } } }
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
- 43
- 44
- 45
- 46
- 47
- 48
- 49
- 50
- 51
- 52
- 53
- 54
- 55
- 56
- 57
- 58
- 59
- 60
- 61
- 62
- 63
- 64
- 65
- 66
- 67
- 68
- 69
声明：本文内容由网友自发贡献，不代表【wpsshop博客】立场，版权归原作者所有，本站不承担相应法律责任。如您发现有侵权的内容，请联系我们。转载请注明出处：https://www.wpsshop.cn/w/Monodyee/article/detail/78916
推荐阅读
相关标签
