从0开始搞懂Diffusion扩散模型_diffusion model

SD已经用了好几次了，每次都在网上下载模型时就迷糊了，为什么会有这么多配置文件，所以下决心写一篇从0开始搞懂SD的文章，包含原理、公式和代码。最后发现SD的内容太多了，所以这篇先搞懂Diffusion吧

SD是一类diffusion扩散模型，其基本原理是对于输入图像x0，在前向阶段对图像逐步施加噪声, 直至图像被破坏变成完全的高斯噪声, 然后在逆向阶段学习从高斯噪声还原为原始图像的过程.

对于一个扩散模型，在前向阶段会对输入图像x0逐步添加噪声，每步的x_{t}只和上一步的x_{t-1}有关，直至最后一步T的xT完全变成纯高斯噪声图像。

逆向阶段则是从高斯噪声图像逐步去噪，恢复原图的过程。这里引用大佬

珍妮的选择的图像，其对于DiffusionModel的博客写的非常好，这篇文章可以说就是学习他的博客的笔记。DiffusionModel其实有很多，但最基础的是DDPM（Denoising Diffusion Probabilistic Model），以此为基础衍生出后续的模型，当然DDPM也不是最早的，但在效果上取得了非常重大的突破。本文也是介绍DDPM为主，顺便介绍一些概率论基础内容为0基础的同学顺利理清逻辑。

扩散模型 (Diffusion Model) 简要介绍与源码分析_diffusion模型_珍妮的选择的博客-CSDN博客

 

所以对于一个训练完毕的扩散模型，只要输入一张高斯噪声图像，就可以恢复出原来的图像。

这里涉及到的概念有高斯噪声：在数学上，高斯噪声是一种通过向输入数据添加均值为零和标准差(σ)的正态分布随机值而产生的噪声。 正态分布，也称为高斯分布，是一种连续概率分布，由其概率密度函数 (PDF) 定义：

 pdf(x) = (1 / (σ * sqrt(2 * π))) * e^(- (x — μ)² / (2 * σ²))

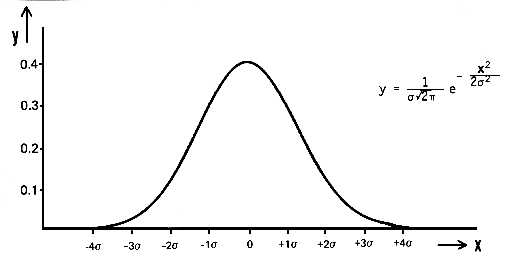
 其中 x 是随机变量，μ 是均值，σ 是标准差。

对图像添加高斯噪声的做法可以是将图像表示为像素值的二维矩阵，然后使用 numpy 库 np.random.randn(rows,cols) 生成具有正态分布的随机值， 并将它们添加到图像的像素值中。 这就会得到添加了高斯噪声的新图像。

深度学习中高斯噪声：为什么以及如何使用 - 知乎 (zhihu.com)

前向阶段：

由于前向过程中图像Xt只和上一时刻X(t-1)有关, 该过程可以视为马尔科夫过程, 满足:

 马尔可夫过程（以马尔科夫链Markov为例） - 知乎 (zhihu.com)

 这里不容易理解的是这个公式（2），里面的 βt ∈ ( 0 , 1 ) 是高斯分布的方差，而方差开根号即为标准差，N是高斯分布的公式，若如果一个随机变量X服从μ 是均值，σ 是标准差这一分布，则记作，σ^2即为方差。所以公式2的意思应该是q(Xt|X(t-1))的计算公式是xt满足均值为sqrt(1-βt)X(t-1)，方差为βtI，而且βt是越来越大的，在实际操作中可以将其定义为是由0.0001 到0.02线性插值（插值数由T决定）

PS:本科的时候没有好好学概率论，现在看真的太痛苦了，高斯分布就一头雾水，再次感谢大佬们的参考文章

那么公式2是怎么来的呢？为什么Xt和X(t-1)就满足这个过程呢？其实是作者建模来的，作者这样子建模也是有理由的，在后续推导过程中就会发现这样子建模的优势就是不管有多少步都满足高斯分布，即能够稳定保证Xt最后收敛到方差为1的标准高斯分布。这一步为什么可以建模呢？因为这是将原图一步步加噪的过程，是自由的！所以我们可以理解β这个参数是噪声的权值，α则是为了满足每一步都是方差为1的高斯分布人为设定的α=1-β，对于这两个参数的理解非常重要！

生成扩散模型漫谈（一）：DDPM = 拆楼 + 建楼 - 科学空间|Scientific Spaces (kexue.fm)

重要概念1：重参数（reparameterization trick） 

重参数技巧在很多工作（gumbel softmax, VAE）中有所引用。

为什么？：如果我们要从某个分布中随机采样(高斯分布)一个样本，这个过程是无法反传梯度的。

怎么做？：把随机性通过一个独立的随机变量(  )引导过去。

例子：如果要从高斯分布 采样一个z，我们可以写成:

上式的z依旧是有随机性的， 且满足均值方差的高斯分布。这里的均值和方差可以是由参数θ的神经网络推断得到的。整个“采样”过程依旧梯度可导，随机性被转嫁到了ε上。

前向过程通过公式可以获得一个重要特性，就是任意时刻的 Xt可以由X0 和 β 表示，这里引用大佬由浅入深了解Diffusion Model - 知乎 (zhihu.com)

的推导过程，这个公式还是很容易看懂的，最开始的Xt就是高斯分布的求值，在这里可以清楚地看到为什么均值项要乘以sqrt(1-β) ，该均值系数能够稳定保证Xt最后收敛到方差为1的标准高斯分布

 逆向阶段：

逆向过程的关键就是给出噪声然后还原为原图像，那么原理是什么呢？

结论1：如果我们能够逐步得到逆转后的分布 q(X(t-1)|Xt) ，就可以从完全的标准高斯分布 Xt∼N(0,1) 还原出原图分布 X0

结论2：如果 q(Xt|X(t−1)) 满足高斯分布且方差β足够小，则q(X(t−1)|Xt)仍然是一个高斯分布。

结论3：使用深度学习模型（参数为 θ，目前主流是U-Net+attention的结构）去预测这样的一个逆向的分布 pθ ：

 这个公式给我看懵了，具体而言就是q(X(t-1)|Xt)不好直接推断，所以用神经网络拟了个计算公式pθ去计算q，其参数是θ，所以要看懂这个公式，我们得知道q(X(t-1)|Xt)具体是什么。

先引入一下贝叶斯公式

 q(X(t-1)|Xt)可以通过x0，和贝叶斯公式推导如下，这里相信概率论和数学和我一样不好的同学是完全看不懂这个式子怎么来的，

首先是为什么q(X(t-1)|Xt)变成了q(X(t-1)|Xt，X0)，这是因为光靠Xt是反推不了这个公式的，所以得把知道X0也当作条件，引入这个公式，来和Xt一起反推X(t-1)。

第二个问题是后面这个式子是怎么得到的？

简单来说就是套贝叶斯公式，B是X(t-1)，P(B)就是q(X(t-1)|X0)，A是Xt，P(A|B)就是q(Xt|X(t-1)，X0)，下面其实就是P(A)，那就说q(Xt|X0)，鄙人是这么理解的，但是鄙人概率论实在学得不好，这里很难理解，如果有错误欢迎指出，后续也会抓紧学习得

 

而这里式中得q(X(t-1)|X0)和q(Xt|X0)是根据之前得推导是已知得高斯分布，所以逻辑上应该是为了方便反推，所以像前文一样构造计算。这里参考大佬的计算过程生成式扩散模型公式推导：贝叶斯角度 - 知乎 (zhihu.com)

 最后的结果计算如下

 而根据之前的结论2，q(X(t-1)|Xt，X0)也是一个高斯分布

 所以就可以将参数对应，

 最终参数对应的式子如下，并且X0可以转换为Xt

 带入公式9，公式10中的x0是根据公式3反推的，公式3是用x0表示xt，公式10就是用xt表示x0。

 可以进一步简化均值，注意此处为真实分布的计算值

 其中式中εt就是神经网络预测的值，Xt则是模型的输入，而计算得到了q（X(t-1)|Xt）就可以一步步往前推了，最终得到X0。

而在DDPM（denoising diffusion probabilistic models）中，此处带上θ为神经网络预测值

OK!前面推导了这么多，我们再次复习重参数技巧，写出Xt计算X(t-1)的公式吧，目前已知

 重参数技巧的核心是通过噪音来引导随机性

 所以我们可以得到X(t-1)=μθ（Xt,t）+*，

 我们现在对于Diffusion的过程应该是理解了，接下来就是损失函数了，毕竟要优化网络模型，Diffusion的损失函数究竟计算了什么呢？

再一次明确Diffusion的目标是为了得到靠谱的以一步步推导出靠谱的原图X0，

具体做法是通过对真实数据分布下，最大化模型预测分布的对数似然，即优化在 x0∼q(x0) 下的 pθ(x0) 交叉熵：

这个式子是怎么来的？

换个思路理解，目前有两个分布，一个是真实的q(x(t-1)|xt)，一个是深度学习模型（Unet）拟合的pθ(x(t-1)|xt)，最终的目标就是让这两个分布趋于一致，而在DDPM中，

 所以两个分布的差别由均值决定，这里涉及到一个计算概念叫做KL散度（这玩意本科概率论应该没学吧，我毫无印象。。。）

Kullback-Leibler(KL)散度介绍 - 知乎 (zhihu.com)

如果是连续变量的，公式如下： 

 

 而在这里，

  

 高斯分布的KL散度_HEGSNS的博客-CSDN博客

 简而言之，用KL散度来表示两个分布的近似程度，然后高斯分布的KL散度计算公式出来以后就是上面的结果，那么就是要优化，这里的Eq(xt|x0)是指整个式子的数学期望，而式中的Xt、X0是 按照q分布的

以gan中的损失函数为例， 

 

这式子的意思如下

 回到L这个式子，里面的均值根据之前的推导和ε（噪音）有关

代入之后获得最后的损失函数 

 最后再梳理一遍整个算法的流程，这里大佬的流程总结非常好

 扩散模型 (Diffusion Model) 简要介绍与源码分析_diffusion模型_珍妮的选择的博客-CSDN博客

 

最后是代码介绍，我这里介绍的是SD模型中的DDPM代码，重点是理解实现逻辑和公式的代码实现。

对于模型推理我们还是先看forward部分，forward部分即前向推理的过程，输入是原图像，可见非常简单，首先是torch.randint生成了一个x.shape[0]大小的时间步t，然后要计算x和t的p_losses，t即公式中的时间步t

    def forward(self, x, *args, **kwargs):
        # b, c, h, w, device, img_size, = *x.shape, x.device, self.image_size
        # assert h == img_size and w == img_size, f'height and width of image must be {img_size}'
        t = torch.randint(0, self.num_timesteps, (x.shape[0],), device=self.device).long()
        return self.p_losses(x, t, *args, **kwargs)

 在p_losses里首先定义了一个正太分布的noise，大小和输入的x_start一致也就是x0，然后是一个q_sample函数，q_sample计算公式如下，Zt即为noise，然后self.model就是Unet推理预估的噪声，Unet的输入是加了噪声之后的Xt和时间步t，输出为预估的噪声

接着是重参数步骤，默认是eps，即target是noise，然后计算损失函数self.get_loss(model_out,target) ，并且要取损失函数的平均值

    def extract_into_tensor(a, t, x_shape):
        b, *_ = t.shape
        out = a.gather(-1, t)//所以t的作用是随机采样，也就是公式中的时间步t
        return out.reshape(b, *((1,) * (len(x_shape) - 1)))
 
    def q_sample(self, x_start, t, noise=None):
        noise = default(noise, lambda: torch.randn_like(x_start))
        return (extract_into_tensor(self.sqrt_alphas_cumprod, t, x_start.shape) * x_start +
                extract_into_tensor(self.sqrt_one_minus_alphas_cumprod, t, x_start.shape) * noise)
 
    
    def p_losses(self, x_start, t, noise=None):
        noise = default(noise, lambda: torch.randn_like(x_start))
        x_noisy = self.q_sample(x_start=x_start, t=t, noise=noise)
        model_out = self.model(x_noisy, t)
 
        loss_dict = {}
        if self.parameterization == "eps":
            target = noise
        elif self.parameterization == "x0":
            target = x_start
        elif self.parameterization == "v":
            target = self.get_v(x_start, noise, t)
        else:
            raise NotImplementedError(f"Parameterization {self.parameterization} not yet supported")
 
        loss = self.get_loss(model_out, target, mean=False).mean(dim=[1, 2, 3])
 
        log_prefix = 'train' if self.training else 'val'
 
        loss_dict.update({f'{log_prefix}/loss_simple': loss.mean()})
        loss_simple = loss.mean() * self.l_simple_weight
 
        loss_vlb = (self.lvlb_weights[t] * loss).mean()
        loss_dict.update({f'{log_prefix}/loss_vlb': loss_vlb})
 
        loss = loss_simple + self.original_elbo_weight * loss_vlb
 
        loss_dict.update({f'{log_prefix}/loss': loss})
 
        return loss, loss_dict

loss_type默认l2，所以是计算二者的mse_loss， 和公式中相同，后续几步中self.l_simple_weight是1，相当于对损失函数进行赋权值，但实际上这里默认都是1或者0，所以最后结果就是mse_loss

所以可见其逻辑就是通过计算两个噪声之间的差异，优化Unet计算噪声的能力，从而在反向过程中，同样输入Xt和时间步t，其可以预估出需要的噪声，从而一步步从高斯噪声图像重建出原图像。 

    def get_loss(self, pred, target, mean=True):
        if self.loss_type == 'l1':
            loss = (target - pred).abs()
            if mean:
                loss = loss.mean()
        elif self.loss_type == 'l2':
            if mean:
                loss = torch.nn.functional.mse_loss(target, pred)
            else:
                loss = torch.nn.functional.mse_loss(target, pred, reduction='none')
        else:
            raise NotImplementedError("unknown loss type '{loss_type}'")
 
        return loss

训练阶段还有一个问题就是self.sqrt_alphas_cumprod也就是公式中的是如何计算得到的，其计算代码如下，可见其是从β计算而来的，那么再看β

    def register_schedule(self, given_betas=None, beta_schedule="linear", timesteps=1000,
                          linear_start=1e-4, linear_end=2e-2, cosine_s=8e-3):
        if exists(given_betas):
            betas = given_betas
        else:
            betas = make_beta_schedule(beta_schedule, timesteps, linear_start=linear_start, linear_end=linear_end,
                                       cosine_s=cosine_s)
        alphas = 1. - betas
        alphas_cumprod = np.cumprod(alphas, axis=0)

beta_schedule一般默认是linear， 所以beta实际上的计算公式就是

betas = (
        torch.linspace(linear_start ** 0.5, linear_end ** 0.5, n_timestep, dtype=torch.float64) ** 2
)

np.cumprod的作用是将alphas进行累乘 

这里回顾一下diffusion的原理 ，可见我的上一篇从0开始搞懂Diffusion扩散模型_fisherisfish的博客-CSDN博客

里面的 βt ∈ ( 0 , 1 ) 是高斯分布的方差，而方差开根号即为标准差，N是高斯分布的公式，若如果一个随机变量X服从μ 是均值，σ 是标准差这一分布，则记作，σ^2即为方差。所以公式2的意思应该是q(Xt|X(t-1))的计算公式是xt满足均值为sqrt(1-βt)X(t-1)，方差为βtI，而且βt是越来越大的，在实际操作中可以将其定义为是由0.0001 到0.02线性插值（插值数由T决定）

def make_beta_schedule(schedule, n_timestep, linear_start=1e-4, linear_end=2e-2, cosine_s=8e-3):
    if schedule == "linear":
        betas = (
                torch.linspace(linear_start ** 0.5, linear_end ** 0.5, n_timestep, dtype=torch.float64) ** 2
        )
 
    elif schedule == "cosine":
        timesteps = (
                torch.arange(n_timestep + 1, dtype=torch.float64) / n_timestep + cosine_s
        )
        alphas = timesteps / (1 + cosine_s) * np.pi / 2
        alphas = torch.cos(alphas).pow(2)
        alphas = alphas / alphas[0]
        betas = 1 - alphas[1:] / alphas[:-1]
        betas = np.clip(betas, a_min=0, a_max=0.999)
 
    elif schedule == "squaredcos_cap_v2":  # used for karlo prior
        # return early
        return betas_for_alpha_bar(
            n_timestep,
            lambda t: math.cos((t + 0.008) / 1.008 * math.pi / 2) ** 2,
        )
 
    elif schedule == "sqrt_linear":
        betas = torch.linspace(linear_start, linear_end, n_timestep, dtype=torch.float64)
    elif schedule == "sqrt":
        betas = torch.linspace(linear_start, linear_end, n_timestep, dtype=torch.float64) ** 0.5
    else:
        raise ValueError(f"schedule '{schedule}' unknown.")
    return betas.numpy()

 训练阶段中还有一个小知识就是对于βα等参数使用了self.register_buffer，回顾模型保存：torch.save(model.state_dict())，model.state_dict()是一个字典，里边存着我们模型各个部分的参数。在model中，我们需要更新其中的参数，训练结束将参数保存下来。但在某些时候，我们可能希望模型中的某些参数参数不更新（从开始到结束均保持不变），但又希望参数保存下来（model.state_dict() ），这是我们就会用到 register_buffer() 。
Pytorch中的register_buffer()_程序员_Iverson的博客-CSDN博客

至此训练过程就已经完全理清了，接着是逆向阶段，又叫采样阶段，采样阶段的入口是DDPM中的sample函数

和forward函数一样简单，函数输入简单来说就是B，C，H，W即图像维度的大小，然后进入p_sample_loop函数

    @torch.no_grad()
    def sample(self, batch_size=16, return_intermediates=False):
        image_size = self.image_size
        channels = self.channels
        return self.p_sample_loop((batch_size, channels, image_size, image_size),
                                  return_intermediates=return_intermediates)

 这里核心的代码就是中间的for循环，首先是生成随机高斯噪音img即论文中的Xt，然后这里的for循环就是将其一步步返回到X0，我们直接进入p_sample这个函数来看

    @torch.no_grad()
    def p_sample_loop(self, shape, return_intermediates=False):
        device = self.betas.device
        b = shape[0]
        img = torch.randn(shape, device=device)
        intermediates = [img]
        for i in tqdm(reversed(range(0, self.num_timesteps)), desc='Sampling t', total=self.num_timesteps):
            img = self.p_sample(img, torch.full((b,), i, device=device, dtype=torch.long),
                                clip_denoised=self.clip_denoised)
            if i % self.log_every_t == 0 or i == self.num_timesteps - 1:
                intermediates.append(img)
        if return_intermediates:
            return img, intermediates
        return img

p_sample这里使用的是论文中的重参数技巧，即输入的是Xt，返回X(t-1)，这里回顾一下基于重参数技巧得到的计算公式

 可见我们要计算平均值和方差，而p_mean_variance函数就是干这件事情。

    @torch.no_grad()
    def p_sample(self, x, t, clip_denoised=True, repeat_noise=False):
        b, *_, device = *x.shape, x.device
        model_mean, _, model_log_variance = self.p_mean_variance(x=x, t=t, clip_denoised=clip_denoised)
        noise = noise_like(x.shape, device, repeat_noise)
        # no noise when t == 0
        nonzero_mask = (1 - (t == 0).float()).reshape(b, *((1,) * (len(x.shape) - 1)))
        return model_mean + nonzero_mask * (0.5 * model_log_variance).exp() * noise

 我们再回顾一下这个均值和方差是怎么来的，值得注意的是在代码中重参数选择eps和x0时结果是不一样的，如果是eps，那么首先都是通过x和t来预估噪音，接着在predict_start_from_noise函数里会计算一下公式

再获得X0之后再根据

 计算均值和方差，这两个计算公式的代码实现我都贴在下面了，比较疑惑的是还多了一步posterior_log_variance_clipped = extract_into_tensor(self.posterior_log_variance_clipped, t, x_t.shape)

而实际在DDPM中

 作者其实给出了解释，因为方差在最开始的时候是0，所以做了处理并转到了log

                # calculations for posterior q(x_{t-1} | x_t, x_0)
        posterior_variance = (1 - self.v_posterior) * betas * (1. - alphas_cumprod_prev) / (
                1. - alphas_cumprod) + self.v_posterior * betas
                 //v_posterior=0.,  # weight for choosing posterior variance as sigma = (1-v) * beta_tilde + v * beta
 
 
        self.register_buffer('posterior_mean_coef1', to_torch(
            betas * np.sqrt(alphas_cumprod_prev) / (1. - alphas_cumprod)))
        self.register_buffer('posterior_mean_coef2', to_torch(
            (1. - alphas_cumprod_prev) * np.sqrt(alphas) / (1. - alphas_cumprod)))
 
 
        # below: log calculation clipped because the posterior variance is 0 at the beginning of the diffusion chain
        self.register_buffer('posterior_log_variance_clipped', to_torch(np.log(np.maximum(posterior_variance, 1e-20))))

    def predict_start_from_noise(self, x_t, t, noise):
        return (
                extract_into_tensor(self.sqrt_recip_alphas_cumprod, t, x_t.shape) * x_t -
                extract_into_tensor(self.sqrt_recipm1_alphas_cumprod, t, x_t.shape) * noise
        )
 
    def p_mean_variance(self, x, t, clip_denoised: bool):
        model_out = self.model(x, t)
        if self.parameterization == "eps":
            x_recon = self.predict_start_from_noise(x, t=t, noise=model_out)
        elif self.parameterization == "x0":
            x_recon = model_out
        if clip_denoised:
            x_recon.clamp_(-1., 1.)
 
        model_mean, posterior_variance, posterior_log_variance = self.q_posterior(x_start=x_recon, x_t=x, t=t)
        return model_mean, posterior_variance, posterior_log_variance
 
 
    def q_posterior(self, x_start, x_t, t):
        posterior_mean = (
                extract_into_tensor(self.posterior_mean_coef1, t, x_t.shape) * x_start +
                extract_into_tensor(self.posterior_mean_coef2, t, x_t.shape) * x_t
        )
        posterior_variance = extract_into_tensor(self.posterior_variance, t, x_t.shape)
        posterior_log_variance_clipped = extract_into_tensor(self.posterior_log_variance_clipped, t, x_t.shape)
        return posterior_mean, posterior_variance, posterior_log_variance_clipped

 获得了均值和方差之后接着往后看

值得一提的是此处的噪声是直接随机生成的高斯噪音，和前面预测的高斯噪音是不同的，最终结果就是基于Xt和重参数技巧计算的X(t-1)，随后便是不断地循环，最终导出最后的图像。

        noise = noise_like(x.shape, device, repeat_noise)
        # no noise when t == 0
        nonzero_mask = (1 - (t == 0).float()).reshape(b, *((1,) * (len(x.shape) - 1)))
        return model_mean + nonzero_mask * (0.5 * model_log_variance).exp() * noise
 
 
def noise_like(shape, device, repeat=False):
    repeat_noise = lambda: torch.randn((1, *shape[1:]), device=device).repeat(shape[0], *((1,) * (len(shape) - 1)))
    noise = lambda: torch.randn(shape, device=device)
    return repeat_noise() if repeat else noise()

最后再提一嘴，在此过程中的Unet模型，我们可以看到在整个前向逆向过程中，调用了两次self.model，在前向过程中，输入的是加了噪声之后的Xt和时间步t，输出为预估的噪声，在采样过程中，则是直接输入此时X和时间步t，然后预估噪声，由此我们其实可以知道，模型预估的是X(t-1)至Xt这一步的噪声，基于此我们来看此模型的实现，在DDPM中模型基于以下代码实现，unet_config来自于config，conditioning_key默认是None

self.model = DiffusionWrapper(unet_config, conditioning_key)
 
//v1_inference.yaml中的unet_config
    unet_config:
      target: ldm.modules.diffusionmodules.openaimodel.UNetModel
      params:
        image_size: 32 # unused
        in_channels: 4
        out_channels: 4
        model_channels: 320
        attention_resolutions: [ 4, 2, 1 ]
        num_res_blocks: 2
        channel_mult: [ 1, 2, 4, 4 ]
        num_heads: 8
        use_spatial_transformer: True
        transformer_depth: 1
        context_dim: 768
        use_checkpoint: True
        legacy: False

接着我们来看一眼DiffusionWrapper，从这我们可以看出conditioning_key是决定有没有额外条件输入的，如果没有的话就是简单的 self.diffusion_model(x, t)，如果有其他的额外条件，则需要另做处理，如果单独看diffusion_model其实就是一个比较简单的Unet，由于此处无法单独debug，所以对于该模型会在后面的SD模型代码讲解时再细讲！

class DiffusionWrapper(pl.LightningModule):
    def __init__(self, diff_model_config, conditioning_key):
        super().__init__()
        self.sequential_cross_attn = diff_model_config.pop("sequential_crossattn", False)
        self.diffusion_model = instantiate_from_config(diff_model_config)
        self.conditioning_key = conditioning_key
        assert self.conditioning_key in [None, 'concat', 'crossattn', 'hybrid', 'adm', 'hybrid-adm', 'crossattn-adm']
 
    def forward(self, x, t, c_concat: list = None, c_crossattn: list = None, c_adm=None):
        if self.conditioning_key is None:
            out = self.diffusion_model(x, t)
        elif self.conditioning_key == 'concat':
            xc = torch.cat([x] + c_concat, dim=1)
            out = self.diffusion_model(xc, t)
        elif self.conditioning_key == 'crossattn':
            if not self.sequential_cross_attn:
                cc = torch.cat(c_crossattn, 1)
            else:
                cc = c_crossattn
            if hasattr(self, "scripted_diffusion_model"):
                # TorchScript changes names of the arguments
                # with argument cc defined as context=cc scripted model will produce
                # an error: RuntimeError: forward() is missing value for argument 'argument_3'.
                out = self.scripted_diffusion_model(x, t, cc)
            else:
                out = self.diffusion_model(x, t, context=cc)
        elif self.conditioning_key == 'hybrid':
            xc = torch.cat([x] + c_concat, dim=1)
            cc = torch.cat(c_crossattn, 1)
            out = self.diffusion_model(xc, t, context=cc)
        elif self.conditioning_key == 'hybrid-adm':
            assert c_adm is not None
            xc = torch.cat([x] + c_concat, dim=1)
            cc = torch.cat(c_crossattn, 1)
            out = self.diffusion_model(xc, t, context=cc, y=c_adm)
        elif self.conditioning_key == 'crossattn-adm':
            assert c_adm is not None
            cc = torch.cat(c_crossattn, 1)
            out = self.diffusion_model(x, t, context=cc, y=c_adm)
        elif self.conditioning_key == 'adm':
            cc = c_crossattn[0]
            out = self.diffusion_model(x, t, y=cc)
        else:
            raise NotImplementedError()
 
        return out

 总结：中间因为其他工作，这篇文章拖了很久，但也总算是写完了，主要介绍了DDPM的原理，包括前向和逆向两个阶段，在前向阶段对原图加高斯噪声，并用Unet训练，Unet的输入是Xt和t，输出是预估的噪声，并与加的高斯噪声计算MSE损失函数，而其原理是计算两个前向过程和逆向过程两个分布的KL散度，此处前向过程是人为设定的高斯分布q(Xt|X(t-1))，其均值和方差平方和等于1，基于此其可以直接从X0推导到Xt，逆向过程则直接给出高斯噪声图像Xt，然后用贝叶斯公式反向推导p(X(t-1)|Xt,X0)，经过训练阶段的Unet可以有效预估让两个分布近似的噪声，然后基于此噪声和Xt逆向推导X(t-1)，再循环此过程，得到最后的输出，也就是生成的图像！