红黑树——C/C++_c++的红黑树是二叉排序树

红黑树

由于红黑树本质上就是一棵二叉查找树，所以在了解红黑树之前，咱们先来看下二叉查找树。

1. 二叉查找树

二叉查找树（Binary Search Tree），是指一棵空树或者具有下列性质的二叉树：

1. 若任意节点的左子树不空，则左子树上所有节点的值均小于它的根节点的值
2. 若任意节点的右子树不空，则右子树上所有节点的值均大于它的根节点的值
3. 任意节点的左、右子树也分别为二叉查找树
4. 没有键值相等的节点（no duplicate nodes）

2. 红黑树

R-B Tree，全称是Red-Black Tree，又称为“红黑树”，它一种特殊的二叉查找树。红黑树的每个节点上都有存储位表示节点的颜色，可以是红(Red)或黑(Black)。

根节点必黑，只能黑连黑，不能红连红； 新增默认是红色，父叔通红就变色，父红叔黑就旋转，哪边黑往哪边转。

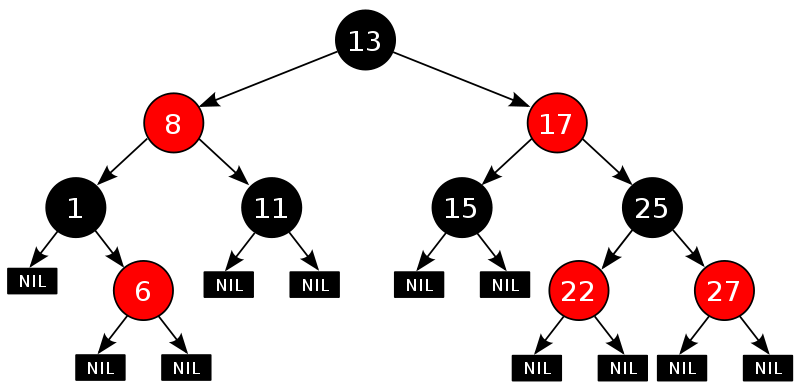
红黑树的特性

1. 每个节点要么是红的，要么是黑的
2. 根节点是黑色
3. 每个叶子节点是黑色
4. 如果一个节点是红色的，则它的子节点必须是黑色的
5. 从任一节点到其每个叶子的所有简单路径都包含相同数目的黑色节点

注意

• 特性(3)中的叶子节点，是指为空(NIL或null)的节点。
• 特性(4)从每个叶子到根的所有路径上不能有两个连续的红色节点

3. 操作

 因为每一个红黑树也是一个特化的二叉查找树，因此红黑树上的只读操作与普通二叉查找树上的只读操作相同。

 在红黑树上进行插入操作和删除操作会导致不再符合红黑树的性质。恢复红黑树的性质需要少量 $\text{O}(\log n)$ 的颜色变更（实际是非常快速的）和不超过三次树旋转（对于插入操作是两次）。虽然插入和删除很复杂，但操作时间仍可以保持为 $\text{O}(\log n)$ 次。

3.0 基础操作

（1）结构体

enum color_t {
    BLACK,
    RED
};

typedef struct _Red_Black_Tree_Node {
    int                          key;
    enum color_t                 color;
    struct _Red_Black_Tree_Node* parent;
    struct _Red_Black_Tree_Node* left;
    struct _Red_Black_Tree_Node* right;
} RBTNode;

RBTNode* NIL = NewNode(0, BLACK, NULL, NULL, NULL);
1
2
3
4
5
6
7
8
9
10
11
12
13
14

（2）获取各种节点

RBTNode* GetParent(RBTNode* n) {
    // Note that parent is set to NULL for the root .
    return n == NULL ? NULL : n->parent;
}

RBTNode* GetGrandParent(RBTNode* n) {
    // Note that it will return NULL if this is root or child of root
    return GetParent(GetParent(n));
}

RBTNode* GetSibling(RBTNode* n) {
    RBTNode* p = GetParent(n);

    // No parent means no sibling.
    if (p == NULL) {
        return NULL;
    }

    if (n == p->left) {
        return p->right;
    } else {
        return p->left;
    }
}

RBTNode* GetUncle(RBTNode* n) {
    RBTNode* p = GetParent(n);

    // No parent means no uncle
    return GetSibling(p);
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31

（3）旋转

 红黑树是基于二叉查找树，当我们在对红黑树进行插入和删除等操作时，对树做了修改，那么可能会违背红黑树的性质。为了继续保持红黑树的性质，我们可以通过对结点进行重新着色，以及对树进行相关的旋转操作，即修改树中某些结点的颜色及指针结构，来达到对红黑树进行插入或删除结点等操作后，继续保持它的性质。

 旋转操作不会导致叶节点顺序的改变（可以理解为旋转操作前后，树的中序遍历结果是一致的），旋转过程中也始终受二叉搜索树的主要性质约束：右子节点比父节点大、左子节点比父节点小。

 尤其需要注意的是，进行右旋转时，旋转前根的左节点的右节点（例如上图中以 B 为根的 $\beta$ 节点）会变成根的左节点，根本身则在旋转后会变成新的根的右节点，而在这一过程中，整棵树一直遵守着前面提到的几个约束。相反的左旋转操作亦然。

注意：这些都有父节点，旋转后新的根节点连接到原来根节点的父节点。

左旋

void RotateLeft(RBTNode* n) {
    RBTNode* nnew = n->right;
    RBTNode* p    = GetParent(n);
    // Since the leaves of a red-black tree are empty,
    // they cannot become internal nodes.
    assert(nnew != NULL);

    n->right   = nnew->left;
    nnew->left = n;
    n->parent  = nnew;
    // Handle other child/parent pointers.
    if (n->right != NIL) {
        n->right->parent = n;
    }

    // Initially n could be the root.
    if (p != NIL) {
        if (n == p->left) {
            p->left = nnew;
        } else if (n == p->right) {
            p->right = nnew;
        }
    }
    nnew->parent = p;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25

右旋

void RotateRight(RBTNode* n) {
    RBTNode* nnew = n->left;
    RBTNode* p    = GetParent(n);
    // Since the leaves of a red-black tree are empty,
    // they cannot become internal nodes.
    assert(nnew != NULL);

    n->left     = nnew->right;
    nnew->right = n;
    n->parent   = nnew;

    // Handle other child/parent pointers.
    if (n->left != NIL) {
        n->left->parent = n;
    }

    // Initially n could be the root.
    if (p != NULL) {
        if (n == p->left) {
            p->left = nnew;
        } else if (n == p->right) {
            p->right = nnew;
        }
    }
    nnew->parent = p;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26

3.1 插入

在下面的示意图中，将要插入的节点标为N(node)，N的父节点标为P(parent)，N的祖父节点标为G(grandfather)，N的叔父节点标为U(uncle)

（1）插入步骤

先构想一下插入步骤

1. 通过二叉查找树的递归方法找到插入位置并将新节点插入
2. 插入后可能不符合性质，需要调整插入结点周围的位置或颜色
3. 最后返回根节点

插入首先以与标准二叉搜索树插入非常相似的方式添加节点，并将其着色为红色。最大的区别在于，在二叉搜索树中，一个新节点被添加为一个叶，而叶在红黑树中不包含任何信息，因此新节点替换了一个现有的叶子，然后添加了两个自己的黑叶子。

RBTNode* Insert(RBTNode* root, RBTNode* n) {
    // Insert new RBTNode into the current tree.
    InsertRecurse(root, n);

    // Repair the tree in case any of the red-black properties have been violated.
    InsertRepairTree(n);

    // Find the new root to return.
    root = n;
    while (GetParent(root) != NULL) {
        root = GetParent(root);
    }
    return root;
}

void InsertRecurse(RBTNode* root, RBTNode* n) {
    // Recursively descend the tree until a leaf is found.
    if (root != NULL) {
        if (n->key < root->key) {
            if (root->left != NIL) {
                InsertRecurse(root->left, n);
                return;
            } else {
                root->left = n;
            }
        } else { // n->key >= root->key
            if (root->right != NIL) {
                InsertRecurse(root->right, n);
                return;
            } else {
                root->right = n;
            }
        }
    }

    // Insert new RBTNode n.
    n->parent = root;
    n->left   = NIL;
    n->right  = NIL;
    n->color  = RED;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41

（2）插入修复

 我们首先以二叉查找树的方法增加节点并标记它为红色。（如果设为黑色，就会导致根到叶子的路径上有一条路上，多一个额外的黑节点，这个是很难调整的。但是设为红色节点后，可能会导致出现两个连续红色节点的冲突，那么可以通过颜色调换（color flips）和树旋转来调整。）下面要进行什么操作取决于其他临近节点的颜色。

有几种红黑树插入需要处理:

1. N为根节点，即红黑树的第一个节点
2. N的父母（P）是黑色
3. P是红色的（所以它不可能是树根），N的叔叔（U）是红色的
4. P是红色的，U是黑色的

void InsertRepairTree(RBTNode* n) {
    if (GetParent(n) == NULL) {
        InsertCase1(n);
    } else if (GetParent(n)->color == BLACK) {
        InsertCase2(n);
    } else if (GetUncle(n) != NIL && GetUncle(n)->color == RED) {
        InsertCase3(n);
    } else {
        InsertCase4(n);
    }
}
1
2
3
4
5
6
7
8
9
10
11

注意：

• 属性1（每个节点都是红色或黑色）和属性3（所有叶子都是黑色）始终有效。
• 属性2（根为黑色）但插入为红色需检查并更正为情形1。
• 属性4（红色节点只有黑色子节点）仅通过添加红色节点、将节点从黑色重新绘制为红色或旋转来受到威胁。
• 属性5（从任何给定节点到其叶的所有路径都具有相同数量的黑色节点）仅通过添加黑色节点、重新绘制节点或旋转来受到威胁。

情形1: 新节点N位于树的根上，没有父节点。在这种情形下，我们把它重绘为黑色以满足性质2。因为它在每个路径上对黑节点数目增加一，性质5符合。

void InsertCase1(RBTNode* n) {
    n->color = BLACK;
}
1
2
3

情形2: 新节点的父节点P是黑色，所以性质4没有失效（新节点是红色的）。在这种情形下，树仍是有效的。性质5也未受到威胁，尽管新节点N有两个黑色叶子子节点；但由于新节点N是红色，通过它的每个子节点的路径就都有同通过它所取代的黑色的叶子的路径同样数目的黑色节点，所以依然满足这个性质。

void InsertCase2(RBTNode* n) {
    // Do nothing since tree is still valid.
    return;
}
1
2
3
4

注意：在下面的情况下，可以假设N有一个祖父母节点G，因为它的父节点P是红色的，如果它是根节点，它将是黑色的。因此，N也具有叔叔节点U，尽管在情况4中它可以是叶。
注意：在其余的情况下，图中显示了父节点P是其父节点的左子节点，即使P可能位于任意一侧。代码示例已经涵盖了这两种可能性。

情况3：如果父节点P和父节点U都是红色的，那么它们都可以重新绘制为黑色，而祖父母G则变为红色以保持属性5（从节点到叶子的所有路径都包含相同数量的黑色节点）。由于通过父节点或父节点的任何路径都必须经过祖父母节点，所以这些路径上的黑色节点数没有改变。但是，如果祖父母G是根，那么它现在可能会违反属性2（根是黑色的），如果它有一个红色的父节点，则它可能违反属性4（每个红色节点的两个子节点都是黑色的）。为了解决这个问题，树的红黑修复过程在G上重新运行。

void InsertCase3(RBTNode* n) {
    GetParent(n)->color      = BLACK;
    GetUncle(n)->color       = BLACK;
    GetGrandParent(n)->color = RED;
    InsertRepairTree(GetGrandParent(n));
}
1
2
3
4
5
6

注意：在余下的情形下，我们假定父节点P是其祖父G的左子节点。如果它是右子节点，情形4和情形4_2中的左和右应当对调。

情况4: 步骤1：父元素P是红色的，但是U叔叔是黑色的（这意味着P的左或右子元素必须是黑色的）。最终目标是将新节点N旋转到祖父位置，但如果N位于G下子树的“内部”（即，如果N是G的右子节点的左子节点或G的左子节点的右子节点），则这将不起作用。在这个例子中，我们通过一个标记为“P”的子树的旋转（在这个例子中，我们通过一个标记为“P”的子树的旋转来增加它的子路径）。但是P和N都是红色的，所以属性5（从一个节点到它的叶子的所有路径包含相同数量的黑色节点）被保留。属性4（每个红色节点的两个子节点都是黑色的）在步骤2中被恢复。

void InsertCase4(RBTNode* n) {
    RBTNode* p = GetParent(n);
    RBTNode* g = GetGrandParent(n);

    if (n == p->right && p == g->left) {
        RotateLeft(p);
        n = n->left;
    } else if (n == p->left && p == g->right) {
        RotateRight(p);
        n = n->right;
    }

    InsertCase4Step2(n);
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14

情况4: 步骤2：新节点N现在确定位于祖父母G下子树的“外部”（左边的子节点或右边的子节点的右边）。在G上做一个右旋转，用P代替G，使P成为N和G的父对象。G是黑色的，它的前一个子P是红色的，因为违反了属性4。切换P和G的颜色。生成的树满足属性4（红色节点有黑色子节点）。从G到N的所有路径都满足了，因为P穿过了所有的路径。

void InsertCase4Step2(RBTNode* n) {
    RBTNode* p = GetParent(n);
    RBTNode* g = GetGrandParent(n);

    if (n == p->left) {
        RotateRight(g);
    } else {
        RotateLeft(g);
    }
    p->color = BLACK;
    g->color = RED;
}
1
2
3
4
5
6
7
8
9
10
11
12

 在上面的算法中，所有的情况只被调用一次，除了在情况3中，它可以递归回使用祖父母节点的情况1，这是唯一一个迭代实现将有效循环的情况。因为在这种情况下，修复问题每次都会升级两个级别（修复祖父节点），所以修复树（其中h是树的高度）最多需要h⁄2次迭代。因为升级的概率随着每次迭代而呈指数级降低，所以平均插入成本实际上是恒定的。

3.2 删除

在下面的示意图中，将要插入的节点标为N(node)，N的父节点标为P(parent)，N的祖父节点标为G(grandfather)，N的叔父节点标为U(uncle)，N的兄弟为 S(sibling)，$S_L$ 称呼S的左儿子，$S_R$ 称呼S的右儿子。

（1）删除步骤

如果需要删除的节点有两个儿子，那么问题可以被转化成删除另一个只有一个儿子的节点的问题（为了表述方便，这里所指的儿子，为非叶子节点的儿子）。对于二叉查找树，在删除带有两个非叶子儿子的节点的时候，我们要么找到它左子树中的最大元素、要么找到它右子树中的最小元素，并把它的值转移到要删除的节点中。我们接着删除我们从中复制出值的那个节点，它必定有少于两个非叶子的儿子。因为只是复制了一个值（没有复制颜色），不违反任何性质，这就把问题简化为如何删除最多有一个儿子的节点的问题。

在本文余下的部分中，我们只需要讨论删除只有一个儿子的节点（如果它两个儿子都为空，即均为叶子，我们任意将其中一个看作它的儿子）:

1. 如果我们删除一个红色节点（此时该节点的儿子将都为叶子节点），它的父亲和儿子一定是黑色的。所以我们可以简单的用它的黑色儿子替换它，并不会破坏性质3和性质4。通过被删除节点的所有路径只是少了一个红色节点，这样可以继续保证性质5。

2. 另一种简单情况是在被删除节点是黑色而它的儿子是红色的时候。如果只是去除这个黑色节点，用它的红色儿子顶替上来的话，会破坏性质5，但是如果我们重绘它的儿子为黑色，则曾经通过它的所有路径将通过它的黑色儿子，这样可以继续保持性质5。

3. 需要进一步讨论的是在要删除的节点和它的儿子二者都是黑色的时候。这是一种复杂的情况（这种情况下该结点的两个儿子都是叶子结点，否则若其中一个儿子是黑色非叶子结点，另一个儿子是叶子结点，那么从该结点通过非叶子结点儿子的路径上的黑色结点数最小为2，而从该结点到另一个叶子结点儿子的路径上的黑色结点数为1，违反了性质5）。我们首先把要删除的节点替换为它的儿子。出于方便，称呼这个儿子为 N（在新的位置上），称呼它的兄弟（它父亲的另一个儿子）为 S。在下面的示意图中，我们还是使用 P 称呼 N 的父亲，$S_L$ 称呼S的左儿子，$S_R$ 称呼S的右儿子。

我们可以使用以下代码执行上面概述的步骤，其中函数 ReplaceNode 将 child 替换为树中 n 的位置。

RBTNode* getSmallestChild(RBTNode* n) {
    if (n->right == NIL) {
        return n;
    }
    return getSmallestChild(n->right);
}

bool DeleteNode(RBTNode* root, int key) {
    if (key < root->key) {
        if (root->left == NIL) {
            return false;
        }
        return DeleteNode(root->left, key);
    } else if (key > root->key) {
        if (root->right == NIL) {
            return false;
        }
        return DeleteNode(root->right, key);
    } else if (key == root->key) {
        if (root->right == NIL) {
            DeleteOneChild(root);
            return true;
        }
        RBTNode* smallest = getSmallestChild(root->left);
        root->key         = smallest->key;
        DeleteOneChild(smallest);
        return true;
    } else {
        return false;
    }
}

void ReplaceNode(RBTNode* n, RBTNode* child) {
    child->parent = n->parent;
    if (n == n->parent->left) {
        n->parent->left = child;
    } else {
        n->parent->right = child;
    }
}

void DeleteOneChild(RBTNode* n) {
    // Precondition: n has at most one non-leaf child.
    RBTNode* child = (n->right == NIL) ? n->left : n->right;
    assert(child);

    // 儿子直接替换
    ReplaceNode(n, child);
    /**
     * 1. 红色
     *      - 替换了，直接释放删除即可
     * 2. 黑色
     *      - 儿子红色，儿子改黑色
     *      - 儿子黑色，依次讨论
     */
    if (n->color == BLACK) {
        if (child->color == RED) {
            child->color = BLACK;
        } else {
            DeleteCase1(child);
        }
    }
    free(n);
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64

（2）删除修复

如果N和它初始的父亲是黑色，则删除它的父亲导致通过N的路径都比不通过它的路径少了一个黑色节点。因为这违反了性质5，树需要被重新平衡。有几种情形需要考虑：

情形1: N是新的根。我们从每个路径中删除了一个黑色节点，新的根是黑色的，因此属性被保留。

void DeleteCase1(RBTNode* n) {
    if (n->parent != NULL) {
        DeleteCase2(n);
    }
}
1
2
3
4
5

注意：在案例2、5和6中，我们假设 N 是其父 P 的左儿子，如果是右儿子，则在这三种情况下，左、右应该颠倒

情形二：S是红色的。在本例中，我们反转P和S的颜色，然后在P处向左旋转，将S变成N的祖父母。注意P必须是黑色的，因为它有一个红色的孩子。结果子树的路径短于一个黑色节点，因此我们还没有完成。现在N有一个黑色的兄弟姐妹和一个红色的父对象，所以我们可以继续执行步骤4、5或6。（它的新兄弟是黑色的，因为它曾经是红色S的子代）在以后的情况下，我们将重新标记N的新兄弟姐妹为S。

void DeleteCase2(RBTNode* n) {
    RBTNode* s = GetSibling(n);

    if (s->color == RED) {
        n->parent->color = RED;
        s->color         = BLACK;
        if (n == n->parent->left) {
            RotateLeft(n->parent);
        } else {
            RotateRight(n->parent);
        }
    }
    DeleteCase3(n);
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14

情形三：P，S，S的孩子都是黑色。在这种情形下，我们简单的重绘S为红色。结果是通过S的所有路径，它们就是以前不通过N的那些路径，都少了一个黑色节点。因为删除N的初始的父亲使通过N的所有路径少了一个黑色节点，这使事情都平衡了起来。但是，通过P的所有路径现在比不通过P的路径少了一个黑色节点，所以仍然违反性质5。要修正这个问题，我们要从情形1开始，在P上做重新平衡处理。

void DeleteCase3(RBTNode* n) {
    RBTNode* s = GetSibling(n);

    if ((n->parent->color == BLACK) && (s->color == BLACK) &&
        (s->left->color == BLACK) && (s->right->color == BLACK)) {
        s->color = RED;
        DeleteCase1(n->parent);
    } else {
        DeleteCase4(n);
    }
}
1
2
3
4
5
6
7
8
9
10
11

情形四：S 和 S的孩子 是黑色，而 P 是红色。在这种情况下，我们只需交换 S 和 P 的颜色。这不会影响经过S的路径上的黑色节点的数量，但它确实会在经过N的路径上的黑色节点的数量上增加一个，以弥补这些路径上删除的黑色节点。

void DeleteCase4(RBTNode* n) {
    RBTNode* s = GetSibling(n);

    if ((n->parent->color == RED) && (s->color == BLACK) &&
        (s->left->color == BLACK) && (s->right->color == BLACK)) {
        s->color         = RED;
        n->parent->color = BLACK;
    } else {
        DeleteCase5(n);
    }
}
1
2
3
4
5
6
7
8
9
10
11

情形5: S是黑色，S的左子项是红色，S的右子项是黑色，N是其父项的左子项。在本例中，我们在S处向右旋转，这样S的左子元素成为S的父元素，而N的新同级元素。然后我们交换S和它的新父对象的颜色。所有的路径仍然有相同数量的黑色节点，但是现在N有一个黑色的同级节点，它的右边的子节点是红色的，所以我们进入到情形6中。N及其父级都不受此转换的影响。（同样，对于案例6，我们将N的新兄弟标记为S）

void DeleteCase5(RBTNode* n) {
    RBTNode* s = GetSibling(n);

    // This if statement is trivial, due to case 2 (even though case 2 changed
    // the sibling to a sibling's child, the sibling's child can't be red, since
    // no red parent can have a red child).
    if (s->color == BLACK) {
        // The following statements just force the red to be on the left of the
        // left of the parent, or right of the right, so case six will rotate
        // correctly.
        if ((n == n->parent->left) && (s->right->color == BLACK) &&
            (s->left->color == RED)) {
            // This last test is trivial too due to cases 2-4.
            s->color       = RED;
            s->left->color = BLACK;
            RotateRight(s);
        } else if ((n == n->parent->right) && (s->left->color == BLACK) &&
                   (s->right->color == RED)) {
            // This last test is trivial too due to cases 2-4.
            s->color        = RED;
            s->right->color = BLACK;
            RotateLeft(s);
        }
    }
    DeleteCase6(n);
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26

情形6： S是黑色，S的右儿子是红色，而N是它父亲的左儿子。在这种情形下我们在N的父亲上做左旋转，这样S成为N的父亲（P）和S的右儿子的父亲。我们接着交换N的父亲和S的颜色，并使S的右儿子为黑色。子树在它的根上的仍是同样的颜色，所以性质3没有被违反。但是，N现在增加了一个黑色祖先：要么N的父亲变成黑色，要么它是黑色而S被增加为一个黑色祖父。所以，通过N的路径都增加了一个黑色节点。

此时，如果一个路径不通过N，则有两种可能性：

• 它通过N的新兄弟。那么它以前和现在都必定通过S和N的父亲，而它们只是交换了颜色。所以路径保持了同样数目的黑色节点。
• 它通过N的新叔父，S的右儿子。那么它以前通过S、S的父亲和S的右儿子，但是现在只通过S，它被假定为它以前的父亲的颜色，和S的右儿子，它被从红色改变为黑色。合成效果是这个路径通过了同样数目的黑色节点。

在任何情况下，在这些路径上的黑色节点数目都没有改变。所以我们恢复了性质4。在示意图中的白色节点可以是红色或黑色，但是在变换前后都必须指定相同的颜色。

void DeleteCase6(RBTNode* n) {
    RBTNode* s = GetSibling(n);

    s->color         = n->parent->color;
    n->parent->color = BLACK;

    if (n == n->parent->left) {
        s->right->color = BLACK;
        RotateLeft(n->parent);
    } else {
        s->left->color = BLACK;
        RotateRight(n->parent);
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14

4. 总结

（1）红黑树的应用

红黑树的时间复杂度为: O(lgn)

1. Java 集合中的 TreeSet、TreeMap
2. C++ STL 中的 set、map
3. Linux 虚拟内存的管理

（2）说明

我们在打印生成树时，一般省略 空节点（NIL）,但是红黑树需要利用底层空节点，所以默认赋了值。

（3）动态演示

Red/Black Tree

（4）全部代码

August-in Github: 红黑树

5. 参考资料

(1) 浅析红黑树（RBTree）原理及实现

(2) 红黑树(一)之 原理和算法详细介绍

(3) 教你透彻了解红黑树

(4) 维基百科：中文版C++ 红黑树、英文版C Red–black tree