全网最通俗易懂的 Self-Attention自注意力机制 讲解_self attention机制

目录

前言

非常非常基础的知识

键值对（Key-Value）注意力

Q K V矩阵

​的意义

结语

---

前言

因工作需要，不得不再次将Transformer从尘封的记忆中取出。

半年前学Transformer的时候只觉得模型好复杂，步骤好复杂，论文读完，想了好几天，感觉还是没有完全搞明白，仅仅是记住了一些专有名词，除了用于吹牛逼其余一无是处，因为内部的机理完全不明白，所以这些名词啊、公式啊转眼就忘。

Self-attention是Transformer最核心的思想，这两天重新阅读了论文，有了一些新的感想，便急忙将其记下，与朋友们共勉。

博主刚开始接触self-attention时，最不理解的地方就是Q K V这三个矩阵以及我们常提起的query查询向量，现在想来，应该是被纷繁复杂的高维矩阵运算难住了，没有真正理解矩阵运算的核心意义。因此，在本文之前，我总结了一点非常非常基础的知识，文中会重新提及这些知识蕴含的思想是如何体现在模型中的。大道至简，我会尽可能将整个Self-attention讲得通俗易懂些。

非常非常基础的知识

1. 向量的内积是什么，如何计算，最重要的，其几何意义是什么？
2. 一个矩阵W与其自身的转置相乘，得到的结果有什么意义？

键值对（Key-Value）注意力

这一节我们首先分析Transformer最核心的部分，我们从公式开始，把每一步都绘制成图，方便读者理解。

键值对Attention最核心的公式如下图。其实这一个公司中蕴含了很多个点，我们一个一个来讲，请各位跟随我的思路，从最核心的部分入手，细枝末节的部分就会豁然开朗。

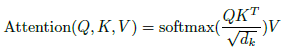
上图是大名鼎鼎的Attention Function，第一眼看过去，哦，两个向量相乘除以一个像是normalization的向量的平方根，然后做一个softmax处理，最后再乘以一个向量。我相信大家第一眼看到这个公式是非常懵逼的，假如你懵逼了，那么下面的这个公式各位是否知道其意义呢？

我们先抛开Q K V三个矩阵不谈，self-attention最原始的形态其实长上面这样。那么这个公式到底什么意思呢？

首先，，一个矩阵乘以它的转置，会得到什么结果，有什么意义呢？

我们知道，矩阵可以看作由一些向量组成，一个矩阵乘以它自己转置的运算，其实可以看成这些向量分别与其他向量计算内积。（此时脑海里想起矩阵乘法的口诀，第一行乘以第一列、第一行乘以第二列......嗯哼，矩阵转置以后第一行不就是第一列吗？这是在计算第一个行向量与自己的内积，第一行乘以第二列是计算第一个行向量与第二个行向量的内积第一行乘以第三列是计算第一个行向量与第三个行向量的内积.....）

回想我们文章开头提出的问题，向量的内积，其几何意义是什么？

答：表征两个向量的夹角，表征一个向量在另一个向量上的投影

记住这个知识点，我们进入一个超级详细的实例：

我们假设 ，其中为一个二维矩阵，为一个行向量（很多教材默认是列向量，但为了方便读者理解，我还是写成行向量）。对应下面的图，对应“早”字embedding之后的结果，以此类推。

下面的运算模拟了一个过程，即。我们来看看其结果究竟有什么意义。

 首先，行向量分别与自己和其他两个行向量做内积（“早”分别与“上”“好”计算内积），得到了一个新的向量。我们回想前文提到的向量的内积表征两个向量的夹角，表征一个向量在另一个向量上的投影。那么新的向量有什么意义呢？是行向量在自己和其他两个行向量上的投影。投影值大和小又有什么意义呢？

投影值大，意味两个向量相关度高。

我们考虑，如果两个向量夹角是90°，那么这两个向量线性无关，完全没有相关性。

更进一步，这两个向量是词向量，是词在高维空间的数值映射。词向量之间相关度高表示什么？是不是在一定程度上（不是完全）表示，在关注词A的时候，应给予词B更多的关注？

上图展示了一个行向量运算的结果，那么矩阵的意义是什么呢？

矩阵是一个方阵，我们以行向量的角度理解，里面保存了每个向量和自己与其他向量进行内积运算的结果。

至此，我们理解了公式中，的意义。我们进一步，Softmax的意义何在呢？请看下图：

 大家都知道softmax的意义就是归一化。

 我们结合上图的理解，softmax之后，这些数字的和为1了，那么attention的核心机制是什么？那不就是加权求和么？那么权重怎么来的呢？就是这些归一化之后的数字。当我们关注“早”这个字的时候，我们应该分配0.4的注意力（attention）给它本身，剩下0.4的注意力给“上”，最后的0.2的注意力给“好”。当然具体到我们的Transformer，就是对应向量的运算了，这是后话。

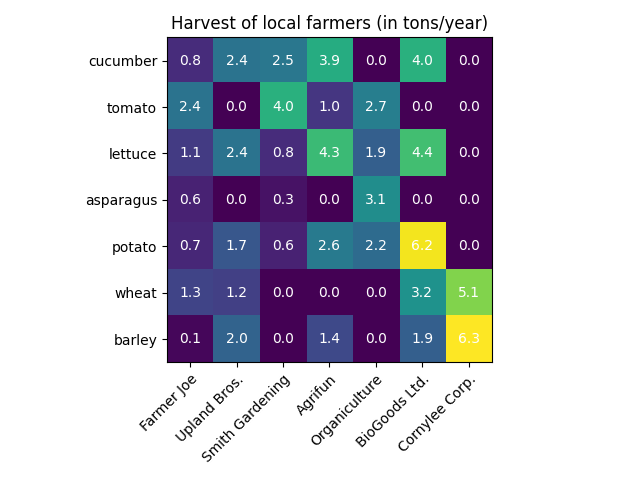
行文至此，我们对这个东西是不是有点熟悉？Python中的热力图Heatmap，其中的矩阵是不是也保存了相似度的结果？

 但，对于，我们仅仅理解了一半，最后一个有什么意义呢？完整的公式究竟表示什么呢？我们继续之前的计算。请看下图。

 我们取的一个行向量举例。这个行向量与的一个列向量相乘，表示什么？

观察上图，行向量与的第一个列向量相乘，得到一个新的行向量，且这个行向量与的维度相同。

在新的向量中，每一个维度的数值都是由三个词向量在这一维度的数值加权求和得来的，这个新的行向量就是"早"字词向量经过注意力机制加权求和之后的表示。

一张更形象的图是这样的，图中右半部分的颜色深浅，其实就是我们上图中黄色向量中数值的大小，意义就是单词之间的相关度（回想之前的内容，相关度其本质是由向量的内积度量的）！

 

 如果你坚持阅读到了这儿，相信你对公式有了更深刻的理解。

接下来就讲一下self-attention公式中的一些细枝末节的问题

Q K V矩阵

 在我们之前的例子中并没有出现Q K V的字眼，因为其并不是公式中最本质的内容。

 

 其实，许多文章里所谓的Q K V矩阵、查询向量之类的字眼，其来源都是与矩阵的乘积，本质上都是的线性变换。那么为什么不直接使用而要对其进行线性变换呢？

当然是为了提升模型的拟合能力，矩阵都是可以训练的，起到一个缓冲的效果。

如果你真正读懂了前文的内容，读懂了这个矩阵的意义，那么你也就理解了所谓查询向量这一类的字眼的含义。

的意义

 假设  都服从均值为0，方差为1的标准高斯分布，那么中元素的均值为0，方差为d。当d变得很大时，中的元素的方差也会变得很大，如果中的元素方差很大，那么的分布会趋于陡峭（分布方差大，分布集中在绝对值大的区域）。总结一下就是的分布会和d有关。因此中每个元素除以后，方差又变为了1。这使得的分布的陡峭程度和d成功解耦，从而使得Transformer在训练过程中的梯度值保持稳定。

怎么样，各位看官听懂没？没听懂的也请不懂装懂。

结语

最后再补充一点，对self-attention来说，它跟每一个input vector都做attention，所以没有考虑到input sequence的顺序。更通俗来讲，大家可以发现我们前文的计算每一个词向量都与其他词向量计算内积，得到的结果丢失了我们原来文本的顺序信息。对比来说，LSTM是对于文本顺序信息的解释是输出词向量的先后顺序，而我们上文的计算对sequence的顺序这一部分则完全没有提及，你打乱词向量的顺序，得到的结果仍然是相同的。

这就牵扯到Transformer的位置编码了，我们按住不表。

后续我将再写一篇关于Transformer的原理讲解，这次坚决不鸽。