期末复习数据结构与算法练习题_假设循环队列中只设 rear 和 quelen 来分别指示队尾元素的位置和队中元素的个数试

第一章 求算法复杂度与频率

设n为正整数，试确定下列各程序中前置以记号@的语句的频度和算法复杂度。
(1) i=1; k=0;
while( i <= n-1)
{ k+=10*i; @ n-1
i++;
}
分析：T(n)=O(n)

(2) i=1; k=0;
do
{ k+=10*i; @ n-1
i++;
}while((i<=n-1);
分析：T(n)=O(n)

(3) i=1; k=0;
while(i<=n-1)
{ i++;
k+=10*i; @ n-1
}
分析：T(n)=O(n)

(4) k=0;
for(i=1; i<=n; i++){
for(j=i; j<=n; j++)
k++; @ n(n+1)/2
}
分析：$T(n)=O(n^2)$

(5) for(i=1; i<=n; i++)
{
for(j=1;j<=i; j++)
{
for(k=1; k<=j; k++)
X += delta; @ n(n+1)(n+2)/6
}
}
分析：$T(n)=O(n^3)$

(6) i=1; j=0;
while( i+j <= n)
{
if(i>j) @ n
j++;
else
i++;
}
分析：
　　通过分析以上程序段，可将i+j看成一个控制循环次数的变量，且每执行一次循环，i+j的值加1。该程序段的主要时间消耗是while循环，而while循环共做了n次，所以该程序段的执行时间为：T(n)=O(n)

第二章 线性表

2.2 填空题。

(1) 在顺序表中插入或删除一个元素，需要平均移动 元素，具体移动的元素个数与 有关。
(2) 顺序表中逻辑上相邻的元素的物理位置 紧邻。单链表中逻辑上相邻的元素的物理位置 紧邻。
(3) 在单链表中，除了首元结点外，任一结点的存储位置由 指示。
(4) 在单链表中设置头结点的作用是 。

1、在顺序表中插入或删除一个元素，需要平均移动（表中一半）元素，具体移动的元素个数与（表长和该元素在表中的位置）有关。
2、顺序表中逻辑上相邻的元素的物理位置（必定）相邻。单链表中逻辑上相邻的元素的物理位置（不一定）相邻。
3、在单链表中，除了首元结点外，任一结点的存储位置由（其直接前驱结点的链域的值）指示。
4、在单链表中设置头结点的作用是（插入和删除元素不必进行特殊处理）。

2.3何时选用顺序表、何时选用链表作为线性表的存储结构为宜?

答：在实际应用中，应根据具体问题的要求和性质来选择顺序表或链表作为线性表的存储结构，通常有以下几方面的考虑：
　1.基于空间的考虑。当要求存储的线性表长度变化不大，易于事先确定其大小时，为了节约存储空间，宜采用顺序表；反之，当线性表长度变化大，难以估计其存储规模时，采用动态链表作为存储结构为好。
　2.基于时间的考虑。若线性表的操作主要是进行查找，很少做插入和删除操作时，采用顺序表做存储结构为宜；反之， 若需要对线性表进行频繁地插入或删除等的操作时，宜采用链表做存储结构。并且，若链表的插入和删除主要发生在表的首尾两端，则采用尾指针表示的单循环链表为宜。

2.7 已知L是带表头结点的非空单链表，且P结点既不是首元结点，也不是尾元结点，试从下列提供的答案中选择合适的语句序列。

a. 删除P结点的直接后继结点的语句序列是____________________。
b. 删除P结点的直接前驱结点的语句序列是____________________。
c. 删除P结点的语句序列是____________________。
d. 删除首元结点的语句序列是____________________。
1
2
3
4

e. 删除尾元结点的语句序列是____________________。
(1) P=P->next;
(2) P->next=P;
(3) P->next=P->next->next;
(4) P=P->next->next;
(5) while(P!=NULL) P=P->next;
(6) while(Q->next!=NULL) { P=Q; Q=Q->next; }
(7) while(P->next!=Q) P=P->next;
(8) while(P->next->next!=Q) P=P->next;
(9) while(P->next->next!=NULL) P=P->next;
(10) Q=P;
(11) Q=P->next;
(12) P=L;
(13) L=L->next;
(14) free(Q);

解：a. (11) (3) (14)
b. (10) (12) (8) (3) (14)
c. (10) (12) (7) (3) (14)
d. (12) (11) (3) (14)
e. (9) (11) (3) (14)

2.8 已知P结点是某双向链表的中间结点，试从下列提供的答案中选择合适的语句序列。

a. 在P结点后插入S结点的语句序列是_______________________。
b. 在P结点前插入S结点的语句序列是_______________________。
c. 删除P结点的直接后继结点的语句序列是_______________________。
d. 删除P结点的直接前驱结点的语句序列是_______________________。
e. 删除P结点的语句序列是_______________________。
(1) P->next=P->next->next;
(2) P->priou=P->priou->priou;
(3) P->next=S;
(4) P->priou=S;
(5) S->next=P;
(6) S->priou=P;
(7) S->next=P->next;
(8) S->priou=P->priou;
(9) P->priou->next=P->next;
(10) P->priou->next=P;
(11) P->next->priou=P;
(12) P->next->priou=S;
(13) P->priou->next=S;
(14) P->next->priou=P->priou;
(15) Q=P->next;
(16) Q=P->priou;
(17) free§;
(18) free(Q);
解：a. (7) (6) (12)(3) （12和3的位置不能反，反了就错了）
b. (8) (5) (13)(4)
c. (15) (1) (11) (18)
d. (16) (2) (10) (18)
e. (14) (9) (17)

2.11 设顺序表va中的数据元素递增有序。试写一算法，将x插入到顺序表的适当位置上，以保持该表的有序性。

解：

Status InsertOrderList(SqList &va,ElemType x)
{
	//在非递减的顺序表va中插入元素x并使其仍成为顺序表的算法
	int i;
	if(va.length==va.listsize)return(OVERFLOW);
	for(i=va.length;i>0,x<va.elem[i-1];i--)
		va.elem[i]=va.elem[i-1];
	va.elem[i]=x;
	va.length++;
	return OK;
}
1
2
3
4
5
6
7
8
9
10
11

其他写法：
答：因已知顺序表L是递增有序表，所以只要从顺序表终端结点（设为i位置元素）开始向前寻找到第一个小于或等于x的元素位置i后插入该位置即可。
　　在寻找过程中，由于大于x的元素都应放在x之后，所以可边寻找，边后移元素，当找到第一个小于或等于x的元素位置i时，该位置也空出来了。
　　算法如下：

//顺序表存储结构如题2.7
　　　　void InsertIncreaseList( Seqlist *L , Datatype x )
　　　　　{ 
　　　　　　int i;
　　　　　　if ( L->length>=ListSize)
　　　　　　　Error(“overflow");
　　　　　　for ( i=L -> length ; i>0 && L->data[ i-1 ] > x ; i--)
　　　　　　　L->data[ i ]=L->data[ i-1 ] ; // 比较并移动元素
　　　　　　L->data[ i ] =x;
　　　　　　L -> length++;
　　　　　}
1
2
3
4
5
6
7
8
9
10
11

2.21 试写一算法，实现顺序表的就地逆置，即利用原表的存储空间将线性表 逆置为 。

解：

// 顺序表的逆置
Status ListOppose_Sq(SqList &L)
{
	int i;
	ElemType x;
	for(i=0;i<L.length/2;i++){
		x=L.elem[i];
		L.elem[i]=L.elem[L.length-1-i];
		L.elem[L.length-1-i]=x;
	}
	return OK;
}
1
2
3
4
5
6
7
8
9
10
11
12

其他写法：
答：
　　要将该表逆置，可以将表中的开始结点与终端结点互换，第二个结点与倒数第二个结点互换，如此反复，就可将整个表逆置了。算法如下：

// 顺序表结构定义同上题

　void ReverseList( Seqlist *L)
　　{
　　　DataType temp ; //设置临时空间用于存放data
　　　int i;
　　　for (i=0;i<L->length/2;i++)//L->length/2为整除运算
　　　　{ temp = L->data[i]; //交换数据
　　　　　L -> data[ i ] = L -> data[ L -> length-1-i];
　　　　　L -> data[ L -> length - 1 - i ] = temp;
　　　　}
　　}
1
2
3
4
5
6
7
8
9
10
11
12

2.24 假设有两个按元素值递增有序排列的线性表A和B，均以单链表作存储结构，请编写算法将A表和B表归并成一个按元素值递减有序（即非递增有序，允许表中含有值相同的元素）排列的线性表C，并要求利用原表（即A表和B表）的结点空间构造C表。

解：

// 将合并逆置后的结果放在C表中，并删除B表
Status ListMergeOppose_L(LinkList &A,LinkList &B,LinkList &C)
{
	LinkList pa,pb,qa,qb;
	pa=A;
	pb=B;
	qa=pa;	// 保存pa的前驱指针
	qb=pb;	// 保存pb的前驱指针
	pa=pa->next;
	pb=pb->next;
	A->next=NULL;
	C=A;
	while(pa&&pb){
		if(pa->data<pb->data){
			qa=pa;
			pa=pa->next;
			qa->next=A->next;	//将当前最小结点插入A表表头
			A->next=qa;
		}
		else{
			qb=pb;
			pb=pb->next;
			qb->next=A->next;	//将当前最小结点插入A表表头
			A->next=qb;
		}
	}
	while(pa){
		qa=pa;
		pa=pa->next;
		qa->next=A->next;
		A->next=qa;
	}
	while(pb){
		qb=pb;
		pb=pb->next;
		qb->next=A->next;
		A->next=qb;
	}
	pb=B;
	free(pb);
	return OK;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42

其他写法：
解：

void reverse_merge(LinkList &A,LinkList &B,LinkList &C)//把元素递增排列的链表A和B合并为C,且C中元素递减排列,使用原空间
{
  pa=A->next;pb=B->next;pre=NULL; //pa和pb分别指向A,B的当前元素
  while(pa||pb)
  {
    if(pa->data<pb->data||!pb)
    {
      pc=pa;q=pa->next;pa->next=pre;pa=q; //将A的元素插入新表
    }
    else
    {
      pc=pb;q=pb->next;pb->next=pre;pb=q; //将B的元素插入新表
    }
    pre=pc;
  }
  C=A;A->next=pc; //构造新表头
}//reverse_merge
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17

分析:本算法的思想是,按从小到大的顺序依次把A和B的元素插入新表的头部pc处,最后处理A或B的剩余元素.

2.31 假设某个单向循环链表的长度大于1，且表中既无头结点也无头指针。已知s为指向链表中某个结点的指针，试编写算法在链表中删除指针s所指结点的前驱结点。

解：

// 在单循环链表S中删除S的前驱结点
Status ListDelete_CL(LinkList &S)
{
	LinkList p,q;
	if(S==S->next)return ERROR;
	q=S;
	p=S->next;
	while(p->next!=S){
		q=p;
		p=p->next;
	}
	q->next=p->next;
	free(p);
	return OK;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15

其他写法：
解：
　　已知指向这个结点的指针是s，那么要删除这个结点的直接前趋结点，就只要找到一个结点，它的指针域是指向s的直接前趋，然后用后删结点法，将结点*s的直接前趋结点删除即可。

算法如下：

　void DeleteNode( ListNode *s)
　　　　{//删除单循环链表中指定结点的直接前趋结点
　　　　　　ListNode *p, *q;
　　　　　　p=s;
　　　　　　while( p->next->next!=s) 
　　　　　　　p=p->next;
　　　　　　//删除结点
　　　　　　q=p->next;
　　　　　　p->next=q->next;
　　　　　　free(p); //释放空间
　　　　}
1
2
3
4
5
6
7
8
9
10
11

注意：
　　若单循环链表的长度等于1，则只要把表删空即可。

2.32 已知有一个单向循环链表，其每个结点中含三个域：pre，data和next，其中data为数据域，next为指向后继结点的指针域，prior也为指针域，但它的值为空(NULL)，试编写算法将此单向循环链表改为双向循环链表，即使prior成为指向前驱结点的指针域。

解：

// 建立一个空的循环链表
Status InitList_DL(DuLinkList &L)
{
	L=(DuLinkList)malloc(sizeof(DuLNode));
	if(!L) exit(OVERFLOW);
	L->pre=NULL;
	L->next=L;
	return OK;
}
	// 向循环链表中插入一个结点
Status ListInsert_DL(DuLinkList &L,ElemType e)
{
	DuLinkList p;
	p=(DuLinkList)malloc(sizeof(DuLNode));
	if(!p) return ERROR;
	p->data=e;
	p->next=L->next;
	L->next=p;
	return OK;
}
	// 将单循环链表改成双向链表
Status ListCirToDu(DuLinkList &L)
{
	DuLinkList p,q;
	q=L;
	p=L->next;
	while(p!=L){
		p->pre=q;
		q=p;
		p=p->next;
	}
	if(p==L) p->pre=q;
	return OK;
}
其他写法：
Status DuLNode_Pre(DuLinkList &L)//完成双向循环链表结点的pre域
{
  for(p=L;!p->next->pre;p=p->next) p->next->pre=p;
  return OK;
}//DuLNode_Pre 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40

第3章 栈和队列

3.2 简述栈和线性表的差别。

解：线性表是具有相同特性的数据元素的一个有限序列。栈是限定仅在表尾进行插入或删除操作的线性表。

3.3 写出下列程序段的输出结果（栈的元素类型SElemType为char）。

void main()
	{
		Stack S;
		char x,y;
		InitStack(S);
		x= ‘c’; y= ‘k’;
		Push(S,x);	Push(S, ‘a’);	Push(S,y);
		Pop(S,x);	Push(S, ‘t’);	Push(S,x);
		Pop(S,x);	Push(S, ‘s’);
		while(!StackEmpty(S)) { Pop(S,y); printf(y); }
		printf(x);
	}
1
2
3
4
5
6
7
8
9
10
11
12

解：stack
void main( ){
Stack S;
Char x,y;
InitStack(S);
x=’c’;y=’k’; //x=‘c’, y=‘k’
Push(S,x); //x=‘c’,y=‘k’,S=“c”
Push(S,’a’); //x=‘c’,y=‘k’,S=“ac”
Push(S,y); //x=‘c’, y=‘k’, S=“kac”
Pop(S,x); //x=‘k’,y=‘k’,S=“ac”
Push(S,’t’); //x=‘k’,y=‘k’,S=“tac”
Push(S,x); //x=‘k’,y=‘k’,S=“ktac”
Pop(S,x); //x=‘k’,y=‘k’ S=“tac”
Push(S,’s’); //x=‘k’,y=‘k’ S=“stac”
while(!StackEmpty(S))
{
Pop(S,y); //依次为y=‘s’,y=‘t’,y=‘a’,y=‘c’
printf(y); //打印依次为s,t,a,c
}
Printf(x);//x=‘k’
}
所以最后应该是stack

3.12 写出以下程序段的输出结果（队列中的元素类型QElemType为char）。

void main()
	{
		Queue Q;
		InitQueue(Q);
		char x= ‘e’, y= ‘c’;
		EnQueue(Q, ‘h’);
		EnQueue(Q, ‘r’);
		EnQueue(Q, y);
		DeQueue(Q, x);
		EnQueue(Q, x);
		DeQueue(Q, x);
		EnQueue(Q, ‘a’);
		While(!QueueEmpty(Q))
		{
			DeQueue(Q,y);
			cout<<y;
		}
		cout<<x;
	}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19

解：char

3.28 假设以带头结点的循环链表表示队列，并且只设一个指针指向队尾元素结点（注意不设头指针），试编写相应的队列初始化、入队列和出队列的算法。

解：

typedef int ElemType;
typedef struct NodeType{
	ElemType data;
	NodeType *next;
}QNode,*QPtr;
typedef struct{
	QPtr rear;
	int size;
}Queue;
Status InitQueue(Queue& q)
{
	q.rear=NULL;
	q.size=0;
	return OK;
}
Status EnQueue(Queue& q,ElemType e)
{
	QPtr p;
	p=new QNode;
	if(!p) return FALSE;
	p->data=e;
	if(!q.rear){
		q.rear=p;
		p->next=q.rear;
	}
	else{
		p->next=q.rear->next;
		q.rear->next=p;
		q.rear=p;
	}
	q.size++;
	return OK;
}
Status DeQueue(Queue& q,ElemType& e)
{
	QPtr p;
	if(q.size==0)return FALSE;
	if(q.size==1){
		p=q.rear;
		e=p->data;
		q.rear=NULL;
		delete p;
	}
	else{
		p=q.rear->next;
		e=p->data;
		q.rear->next=p->next;
		delete p;
	}
	q.size--;
	return OK;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52

其他解法：

3.13 假设以带头结点的循环链表表示队列，并且只设一个指针指向队尾元素站点(注意不设头指针) ，试编写相应的置空队、判队空 、入队和出队等算法。

解：算法如下：

//先定义链队结构:
　typedef struct queuenode{
　　　Datatype data;
　　　struct queuenode *next;
　　}QueueNode; //以上是结点类型的定义
　typedef struct{
　　　queuenode *rear;
　　}LinkQueue; //只设一个指向队尾元素的指针
1
2
3
4
5
6
7
8

(1)置空队

void InitQueue( LinkQueue *Q)
　　　{ //置空队：就是使头结点成为队尾元素
　　　　QueueNode *s;
　　　　Q->rear = Q->rear->next;//将队尾指针指向头结点
　　　　while (Q->rear!=Q->rear->next)//当队列非空，将队中元素逐个出队
　　　　　{s=Q->rear->next;
　　　　　　Q->rear->next=s->next;
　　　　　　free(s);
　　　　　}//回收结点空间
　　　}
1
2
3
4
5
6
7
8
9
10

(2)判队空

int EmptyQueue( LinkQueue *Q)
　　　{ //判队空
　　　　//当头结点的next指针指向自己时为空队
　　　　return Q->rear->next->next==Q->rear->next;
　　　}

(3)入队

void EnQueue( LinkQueue *Q, Datatype x)
　　　{ //入队
　　　　//也就是在尾结点处插入元素
　　　　QueueNode *p=(QueueNode *) malloc (sizeof(QueueNode));//申请新结点
　　　　p->data=x; p->next=Q->rear->next;//初始化新结点并链入
　　　　Q-rear->next=p; 
　　　　Q->rear=p;//将尾指针移至新结点
　　　}
1
2
3
4
5
6
7
8

(4)出队

Datatype DeQueue( LinkQueue *Q)
　　　{//出队,把头结点之后的元素摘下
　　　　Datatype t;
　　　　QueueNode *p;
　　　　if(EmptyQueue( Q ))
　　　　　　Error("Queue underflow");
　　　　p=Q->rear->next->next; //p指向将要摘下的结点
　　　　x=p->data; //保存结点中数据
　　　　if (p==Q->rear)
　　　　　{//当队列中只有一个结点时，p结点出队后，要将队尾指针指向头结点
　　　　　　Q->rear = Q->rear->next; Q->rear->next=p->next;}
　　　　else 
　　　　　　Q->rear->next->next=p->next;//摘下结点p
　　　　free(p);//释放被删结点
　　　　return x;
　　　}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16

3.30 假设将循环队列定义为:以域变量rear和length分别指示循环队列中队尾元素的位置和内含元素的个数。试给出此循环队列的队满条件，并写出相应的入队列和出队列的算法（在出队列的算法中要返回队头元素）。

解：

#define MaxQSize	4
typedef int ElemType;
typedef struct{
	ElemType *base;
	int rear;
	int length;
}Queue;
Status InitQueue(Queue& q)
{
	q.base=new ElemType[MaxQSize];
	if(!q.base) return FALSE;
	q.rear=0;
	q.length=0;
	return OK;
}
Status EnQueue(Queue& q,ElemType e)
{
	if((q.rear+1)%MaxQSize==(q.rear+MaxQSize-q.length)%MaxQSize)
		return FALSE;
	else{
		q.base[q.rear]=e;
		q.rear=(q.rear+1)%MaxQSize;
		q.length++;
	}
	return OK;
}
Status DeQueue(Queue& q,ElemType& e)
{
	if((q.rear+MaxQSize-q.length)%MaxQSize==q.rear)
		return FALSE;
	else{
		e=q.base[(q.rear+MaxQSize-q.length)%MaxQSize];
		q.length--;
	}
	return OK;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36

其他写法：

3.15 假设循环队列中只设rear和quelen 来分别指示队尾元素的位置和队中元素的个数，试给出判别此循环队列的队满条件，并写出相应的入队和出队算法，要求出队时需返回队头元素。

解：根据题意，可定义该循环队列的存储结构：

　#define QueueSize 100 
　typedef char Datatype ; //设元素的类型为char型
　typedef struct {
　　　int quelen;
　　　int rear;
　　　Datatype Data[QueueSize];
　　}CirQueue; 
　CirQueue *Q;
1
2
3
4
5
6
7
8

循环队列的队满条件是：Q->quelen== QueueSize
　　知道了尾指针和元素个数，当然就能计算出队头元素的位置。算法如下：
　(1)判断队满

int FullQueue( CirQueue *Q)
　　　　{//判队满,队中元素个数等于空间大小
　　　　　　return Q->quelen== QueueSize;
　　　　}
1
2
3
4

(2)入队

void EnQueue( CirQueue *Q, Datatype x)
　　　　{// 入队
　　　　　if(FullQueue( Q))
　　　　　　Error("队已满，无法入队");
　　　　　Q->Data[Q->rear]=x;
　　　　　Q->rear=(Q->rear+1)%QueueSize;//在循环意义上的加1
　　　　　Q->quelen++;
　　　　}
1
2
3
4
5
6
7
8

(3)出队

Datatype DeQueue( CirQueue *Q)
　　　　{//出队
　　　　　if(Q->quelen==0)
　　　　　　Error("队已空，无元素可出队");
　　　　　int tmpfront; //设一个临时队头指针
　　　　　tmpfront=(QueueSize+Q->rear - Q->quelen+1)%QueueSize;//计算头指针位置
　　　　　Q->quelen--;
　　　　　return Q->Data[tmpfront];
　　　　}
1
2
3
4
5
6
7
8
9

第六章树和二叉树

6.3 试分别画出具有3个结点的树和3个结点的二叉树的所有不同形态。

解：含三个结点的树只有两种:(1)和(2)；而含3个结点的二叉树可能有下列3种形态:(一)，(二)，(三)，(四)，(五)。

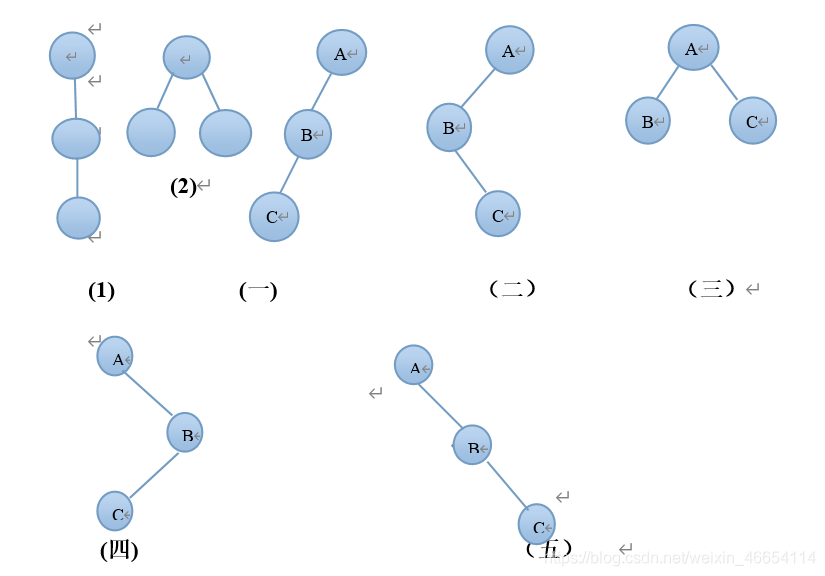
注意，(2)和(三)是完全不同的结构。

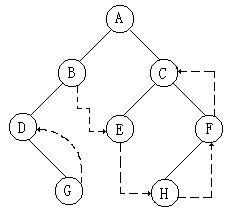
6.15 请对右图所示二叉树进行后序线索化，为每个空指计建立相应的前驱或后继线索

解：

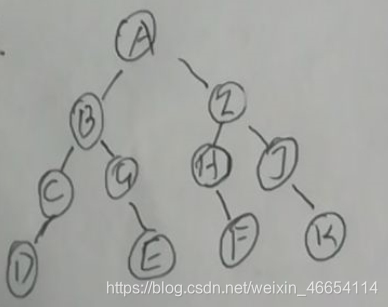
6.27假设一棵二叉树的先序序列为EBADCFHGIKJ和中序序列为ABCDEFGHIJK。请画出该树。

解：

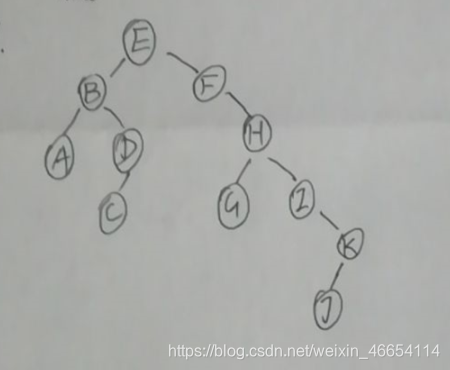
6.28假设一棵二叉树的中序序为DCBGEAHFIJK和后序序列为DCEGBFHKJIA.请画出该树。

解：