- 1利用python画热力图_python 热力图
- 2【JavaEE 初阶(一)】初识线程
- 3H3C—S5560X 交换机mac地址绑定与解绑_华三交换机mac地址绑定命令
- 4crossover 24.0.0 for mac安装win软件方法【2024详解】_crossover24.0
- 5【项目篇1】一个在线OJ系统
- 6ChatGPT之父撰文:《万物摩尔定律》出现,这场革命将创造惊人的财富
- 7Github在开启2FA(双重身份验证)的时候Country- code 没有中国区+86的解决办法,未解决_github不支持+86
- 8动态链表数据结构(头插法和尾插法)
- 9Dockerfile构建redis镜像
- 10数据可视化之通过pyecharts建立可视化用户登录时间热力图_利用pyecharts绘制某门户网站模块访问的热力图,具体访问量数据自拟
FIR滤波器与IIR滤波器的区别与特点
赞
踩
目录
FIR滤波器与IIR滤波器的区别与特点
FIR是有限冲击响应;IIR是无限冲击响应。
FIR和IIR滤波器的一个主要区别:FIR是线性相位,IIR为非线性相位(双线性变换法)。
对于非线性相位会造成的影响,可以这样考虑:对于输入的不同频率分量,造成的相位差与频率不成正比,则输出时不同频率分量的叠加的相位情况和输入时有变化,得到的通带信号产生失真。

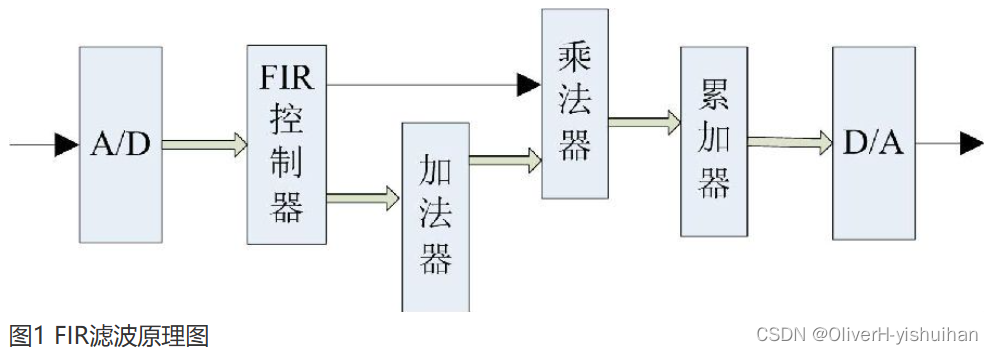
FIR滤波器定义:
FIR滤波器是有限长单位冲激响应滤波器,又称为非递归型滤波器,是数字信号处理系统中最基本的元件,它可以在保证任意幅频特性的同时具有严格的线性相频特性,同时其单位抽样响应是有限长的,因而滤波器是稳定的系统。
特点:
- FIR滤波器的最主要的特点是没有反馈回路,稳定性强,故不存在不稳定的问题;
- FIR具有严格的线性相位,幅度特性随意设置的同时,保证精确的线性相位;
- FIR设计方式是线性的,硬件容易实现;
- FIR相对IIR滤波器而言,相同性能指标时,阶次较高,对CPU的性能要去较高。
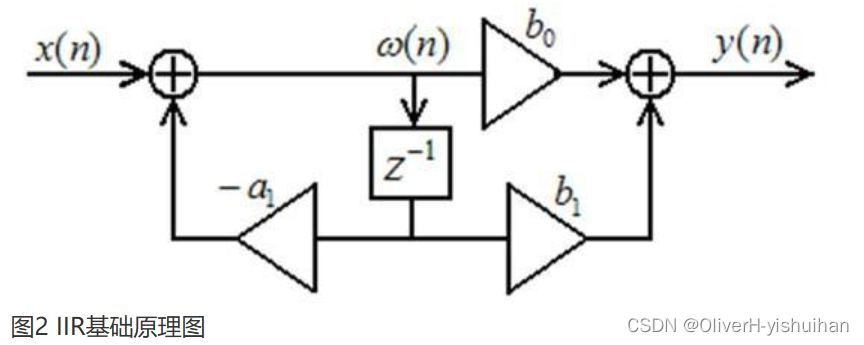
IIR滤波器定义:
IIR滤波器是无限脉冲响应滤波器,又称递归型滤波器,即结构上带有反馈环路。
特点:
- IIR数字滤波器的系统函数可以写成封闭函数的形式,具有反馈回路;
- IIR数字滤波器的相位非线性,相位特性不好控制,随截止频率变化而变化,对相位要求较高时,需加相位校准网络;
- IIR滤波器有历史的输出参与反馈,同FIR相比在相同阶数时取得更好的滤波效果;
- IIR数字滤波器采用递归型结构,由于运算中的舍入处理,使误差不断累积,有时会产生微弱的寄生振荡。
区别:
- 稳定性:由于FIR滤波器没有反馈回路,稳定性要强于IIR;
- 相位特性:FIR 为线性相位延迟,IIR 为非线性相位延迟。
- IIR滤波器存在非线性相位延迟,校正时需要双向滤波进行校正,复杂不易控制;FIR滤波器为线性延迟,可通过左右平移的方式直接校正,误差小。
- 信号处理速度:FIR的滤波输出取决于当前输入数据和历史输入数据,IIR的滤波输出取决于当前输入数据、历史输入数据和历史输出数据。
以基于 FPGA硬件的数字滤波器为例,FIR在处理信号时不需等待前一个信号的滤波输出,只需要考虑输入数据便可实时滤波;IIR需要等待上一个信号的滤波输出,存在一定的时间延迟,所以处理速度上没有FIR快。
IIR与FIR滤波器各有所长,所以在实际应用时应该从多方面考虑来加以选择。从使用要求上来看,在对相位要求不敏感的场合,如语言通信等,选用IIR较为合适,这样可以充分发挥其经济高效的特点;对于图像信号处理,数据传输等以波形携带信息的系统,则对线性相位要求较高,采用FIR滤波器较好。当然,在实际应用中可能还要考虑更多方面的因素。
不论IIR和FIR,阶数越高,信号延迟越大;同时在IIR滤波器中,阶数越高,系数的精度要求越高,否则很容易造成有限字长的误差使极点移到单位园外。因此在阶数选择上是综合考虑的。

IIR滤波器有以下几个特点:
1、IIR数字滤波器的系统函数可以写成封闭函数的形式。
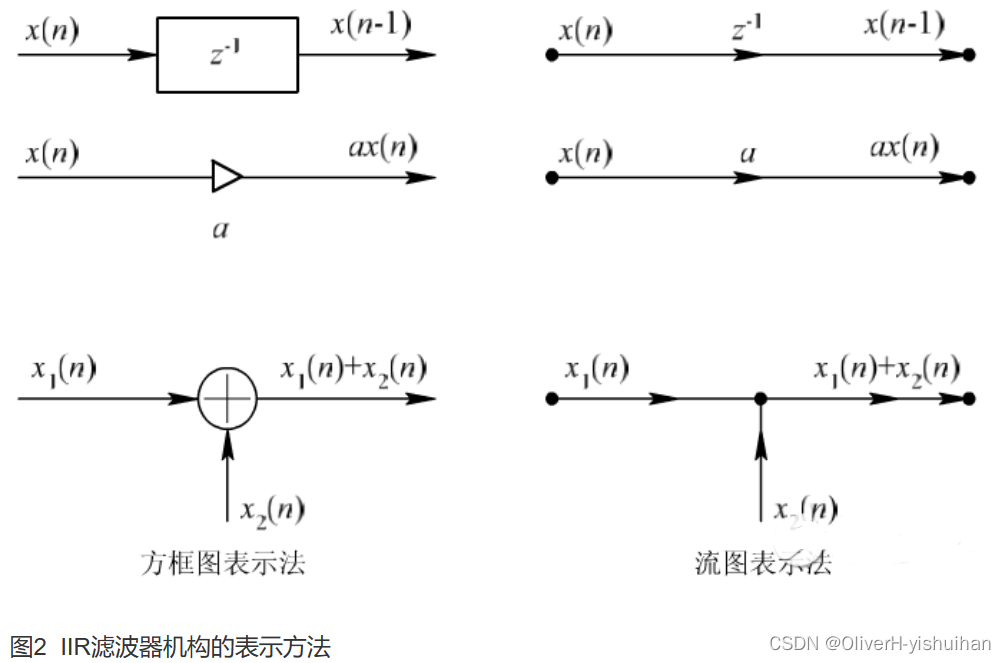
2、IIR数字滤波器采用递归型结构,即结构上带有反馈环路。IIR滤波器运算结构通常由延时、乘以系数和相加等基本运算组成,可以组合成直接型、正准型、级联型、并联型四种结构形式,都具有反馈回路。由于运算中的舍入处理,使误差不断累积,有时会产生微弱的寄生振荡。
3、IIR数字滤波器可以借助成熟的模拟滤波器的成果,如巴特沃斯、契比雪夫和椭圆滤波器等,有现成的设计数据或图表可查,其设计工作量比较小,对计算工具的要求不高。在设计一个IIR数字滤波器时,我们根据指标先写出模拟滤波器的公式,然后通过一定的变换,将模拟滤波器的公式转换成数字滤波器的公式。
4、IIR数字滤波器的相位特性不好控制,对相位要求较高时,需加相位校准网络。
在 matlab下设计 IIR滤波器可使用 buttterworth函数设计出巴特沃斯滤波器,使用 cheby1函数设计出契比雪夫i型滤波器,使用 cheby2设计出契比雪夫II型滤波器,使用 ellipord函数设计出椭圆滤波器。
与FIR滤波器的设计不同,IIR滤波器设计时的阶数不是由设计者指定,而是根据设计者输入的各个滤波器参数(截止频率、通带滤纹、阻带衰减等),由软件设计出满足这些参数的最低滤波器阶数。在matlab下设计不同类型IIR滤波器均有与之对应的函数用于阶数的选择。
IIR单位响应为无限脉冲序列,FIR单位响应为有限的。
IIR幅频特性精度很高,不是线性相位的,可以应用于对相位信息不敏感的音频信号上;FIR幅频特性精度较之于IIR低,但是线性相位,就是不同频率分量的信号经过FIR滤波器后他们的时间差不变。这是很好的性质。
另外有限的单位响应也有利于对数字信号的处理,便于编程,用于计算的时延也小,这对实时的信号处理很重要。

IIR与FIR数字滤波器的比较:
1、从性能上比较
从性能上来说,IIR滤波器传输函数的极点可位于单位圆内的任何地方,因此可用较低的阶数获得高的选择性,所用的存贮单元少,所以经济而效率高。但是这个高效率是以相位的非线性为代价的。选择性越好,则相位非线性越严重。相反,FIR滤波器却可以得到严格的线性相位,然而由于FIR滤波器传输函数的极点固定在原点(输出只与有限项输入有关,所以传递函数分母为1,极点在零点),所以只能用较高的阶数达到高的选择性;对于同样的滤波器设计指标,FIR滤波器所要求的阶数可以比IIR滤波器高5~10倍,结果,成本较高,信号延时也较大;如果按相同的选择性和相同的线性要求来说,则IIR滤波器就必须加全通网络进行相位较正,同样要大增加滤波器的节数和复杂性。
2、从结构上比较
IIR滤波器必须采用递归结构,极点位置必须在单位圆内,否则系统将不稳定。另外,在这种结构中,由于运算过程中对序列的舍入处理,这种有限字长效应有时会引入寄生振荡。相反,FIR滤波器主要采用非递归结构,不论在理论上还是在实际的有限精度运算中都不存在稳定性问题,运算误差也较小。此外,FIR滤波器可以采用快速傅里叶变换算法,在相同阶数的条件下,运算速度可以快得多。


