深度学习推荐系统中各类流行的Embedding方法（下）_embedding工具项目推荐

• 我的个人微信公众号： Microstrong
• 微信公众号ID： MicrostrongAI
• 微信公众号介绍： Microstrong(小强)同学主要研究机器学习、深度学习、推荐系统、自然语言处理、计算机视觉相关内容，分享自己在学习过程中的读书笔记！期待您的关注，欢迎一起学习交流进步！
• 我的知乎主页： https://www.zhihu.com/people/MicrostrongAI/activities
• Github： https://github.com/Microstrong0305
• 个人博客： https://blog.csdn.net/program_developer
• 本文首发在我的微信公众号里，地址：https://mp.weixin.qq.com/s/N76XuNJ7yGzdP6NHk2Rs-w，如有公式和图片不清楚，可以在我的微信公众号里阅读。

Embedding技术概览：

对其它Embedding技术不熟悉，可以看我的上一篇文章：

深度学习推荐系统中各类流行的Embedding方法（上）地址：https://mp.weixin.qq.com/s/D57jP5EwIx4Y1n4mteGOjQ

1. Graph Embedding简介

Word2Vec和其衍生出的Item2Vec类模型是Embedding技术的基础性方法，二者都是建立在“序列”样本（比如句子、用户行为序列）的基础上的。在互联网场景下，数据对象之间更多呈现的是图结构，所以Item2Vec在处理大量的网络化数据时往往显得捉襟见肘，在这样的背景下，Graph Embedding成了新的研究方向，并逐渐在深度学习推荐系统领域流行起来。

Graph Embedding也是一种特征表示学习方式，借鉴了Word2Vec的思路。在Graph中随机游走生成顶点序列，构成训练集，然后采用Skip-gram算法，训练出低维稠密向量来表示顶点。之后再用学习出的向量解决下游问题，比如分类，或者连接预测问题等。可以看做是两阶段的学习任务，第一阶段先做无监督训练生成表示向量，第二阶段再做有监督学习，解决下游问题。

总之，Graph Embedding是一种对图结构中的节点进行Embedding编码的方法。最终生成的节点Embedding向量一般包含图的结构信息及附近节点的局部相似性信息。不同Graph Embedding方法的原理不尽相同，对于图信息的保留方式也有所区别，下面就介绍几种主流的Graph Embedding方法和它们之间的区别与联系。

2. DeepWalk-Graph Embedding早期技术

早期，影响力较大的Graph Embedding方法是于2014年提出的DeepWalk，它的主要思想是在由物品组成的图结构上进行随机游走，产生大量物品序列，然后将这些物品序列作为训练样本输入Word2Vec进行训练，得到物品的Embedding。因此，DeepWalk可以被看作连接序列Embedding和Graph Embedding的过渡方法。

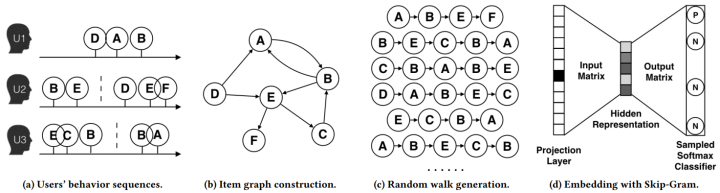
论文《Billion-scale Commodity Embedding for E-commerce Recommendation in Alibaba》用上图所示的方法展现了DeepWalk的算法流程。DeepWalk算法的具体步骤如下：

• 图（a）是原始的用户行为序列。
• 图（b）基于这些用户行为序列构建了物品关系图。可以看出，物品A和B之间的边产生的原因是用户U1先后购买了物品A和物品B。如果后续产生了多条相同的有向边，则有向边的权重被加强。在将所有用户行为序列都转换成物品关系图中的边之后，全局的物品关系图就建立起来了。
• 图（c）采用随机游走的方式随机选择起始点，重新产生物品序列。
• 将这些物品序列输入图（d）所示的Word2Vec模型中，生成最终的物品Embedding向量。

在上述DeepWalk的算法流程中，唯一需要形式化定义的是随机游走的跳转概率，也就是到达结点 $v_i$ 后，下一步遍历 $v_i$ 的邻接点 $v_j$ 的概率。如果物品关系图是有向有权图，那么从节点 $v_i$ 跳转到节点 $v_j$ 的概率定义如下式所示。
P ( v j ∣ v i ) = { M i j ∑ j ∈ N + ( v i ) M i j , v j ∈ N + ( v i ) 0 , e i j ∉ ε P(v_{j}|v_{i}) =\left\{

$$\begin{aligned} \frac{M_{ij}}{\sum_{j\in N_{+}(v_{i})}^{}{M_{ij}}} &, v_{j}\in N_{+}(v_{i}) \\ 0 &, e_{ij} \notin \varepsilon \\ \end{aligned}$$ \right. P(vj​∣vi​)=⎩⎪⎨⎪⎧​∑j∈N+​(vi​)​Mij​Mij​​0​,vj​∈N+​(vi​),eij​∈/​ε​

其中 $\epsilon$ 是物品关系图中所有边的集合， $N_{+}(v_i)$ 是节点 $v_i$ 所有的出边集合， $M_{ij}$ 是节点 $v_i$ 到节点 $v_j$ 边的权重，即DeepWalk的跳转概率就是跳转边的权重占所有相关出边权重之和的比例。

如果物品关系图是无向无权图，那么跳转概率将是上式的一个特例，即权重 $M_{ij}$ 将为常数$1$，且 $N_{+}(v_i)$ 应是节点 $v_i$ 所有“边”的集合，而不是所有“出边”的集合。

注意： 在DeepWalk论文中，作者只提出DeepWalk用于无向无权图。DeepWalk用于有向有权图的内容是阿里巴巴论文《Billion-scale Commodity Embedding for E-commerce Recommendation in Alibaba》中提出的Base Graph Embedding（BGE）模型，其实该模型就是对DeepWalk模型的实践，本文后边部分会讲解该模型。

DeepWalk相关论文：

【1】Perozzi B, Alrfou R, Skiena S, et al. DeepWalk: online learning of social representations[C]. knowledge discovery and data mining, 2014: 701-710.

【2】Wang J, Huang P, Zhao H, et al. Billion-scale Commodity Embedding for E-commerce Recommendation in Alibaba[C]. knowledge discovery and data mining, 2018: 839-848.

3. LINE-DeepWalk的改进

DeepWalk使用DFS（Deep First Search，深度优先搜索）随机游走在图中进行节点采样，使用Word2Vec在采样的序列上学习图中节点的向量表示。LINE（Large-scale Information Network Embedding）也是一种基于邻域相似假设的方法，只不过与DeepWalk使用DFS构造邻域不同的是，LINE可以看作是一种使用BFS（Breath First Search，广度优先搜索）构造邻域的算法。

在Graph Embedding各个方法中，一个主要区别是对图中顶点之间的相似度的定义不同，所以先看一下LINE对于相似度的定义。

3.1 LINE定义图中节点之间的相似度

现实世界的网络中，相连接的节点之间存在一定的联系，通常表现为比较相似或者在向量空间中距离接近。对于带权网络来说，节点之间的权越大，相似度会越高或者距离越接近，这种关系称为一阶近邻。一阶近邻关系用于描述图中相邻顶点之间的局部相似度， 形式化描述为若顶点$u$、$v$之间存在直连边，则边权$w_{uv}$即为两个顶点的相似度，若不存在直连边，则一阶相似度为$0$。 如下图所示，$6$和$7$之间存在直连边，且边权较大（表现为图中顶点之间连线较粗），则认为两者相似且一阶相似度较高，而$5$和$6$之间不存在直连边，则两者间一阶相似度为$0$。

但是，网络中的边往往比较稀疏，仅仅依靠一阶近邻关系，难以描述整个网络的结构。论文中定义了另外一种关系叫做二阶近邻。例如下图中的网络，节点$5$和节点$1,2,3,4$相连，节点$6$也和节点$1,2,3,4$相连，虽然节点$5$和$6$之间没有直接联系，但是节点$5$和$6$之间很可能存在某种相似性。举个例子，在社交网络中，如果两个人的朋友圈重叠度很高，或许两个人之间具有相同的兴趣并有可能成为朋友；在NLP中，如果不同的词经常出现在同一个语境中，那么两个词很可能意思相近。

LINE通过捕捉网络中的一阶近邻关系和二阶近邻关系，更加完整地描述网络。并且LINE适用于有向图、无向图、有权图、无权图。

3.2 LINE算法模型

（1）一阶近邻关系模型

一阶近邻关系模型中定义了两个概率，一个是联合概率，如下公式所示：
$$p_1(v_i,v_j)=1+exp(-{\vec{u}}_i^T\cdot u$$