大模型高效微调-LoRA原理详解和训练过程深入分析

博客首发于我的知乎，详见：https://zhuanlan.zhihu.com/p/702629428

一、LoRA原理

LoRA(Low-Rank Adaptation of LLMs)，即LLMs的低秩适应，是参数高效微调最常用的方法。

LoRA的本质就是用更少的训练参数来近似LLM全参数微调所得的增量参数，从而达到使用更少显存占用的高效微调。

1.1 问题定义

LoRA与训练目标是解耦的，但本文设定就是语言模型建模。

以下将给出语言建模(可自然推广到序列建模)的基本符号定义，即最大化给定提示的条件概率(本质是极大似然估计)。

The maximization of conditional probabilities given a task-specific prompt

给定一个参数为$\mathbf{\Phi}$预训练的自回归语言模型$ P_{\Phi}(y|x)$。

$x$为输入，$y$为输出

note: 为与原文符号一致，下文$\mathbf{\Phi}$、$\mathbf{\Theta}$、$\mathbf{W}$均表示模型参数

全参数微调

每次full fine-tuning训练，学一个 $\Delta \mathbf{\Phi}$，$|\Delta \mathbf{\Phi}|$ 参数量大hold不住

语言模型的条件概率分布建模目标

高效微调

$ \Delta \mathbf{\Phi}$ 是特定于下游任务的增量参数

LoRA将 $ \Delta \mathbf{\Phi}=\Delta \mathbf{\Phi}(\Theta)$ ，用参数量更少的$ \mathbf{\Theta}$来编码(低秩降维表示来近似), $|\mathbf{\Phi}| << | \mathbf{\Theta}|$

LoRA训练目标

Transformer架构参数

Transformer层的输入和输出维度大小 $d_{model}$

$\mathbf{W_q}$、$\mathbf{W_k}$、$\mathbf{W_v}$,和$\mathbf{W_o}$分别代表自注意力的query、key、value和output投影矩阵

$\mathbf{W}$或$\mathbf{W}_0$代表预训练的权重矩阵

$∆\mathbf{W}$是微调后得到的增量参数矩阵(训练后，优化算法在参数上的累计更新量)

$r$代表LoRA模块的秩

1.2 LoRA简介

LoRA的核心思想是，在冻结预训练模型权重后，将可训练的低秩分解矩阵注入到的Transformer架构的每一层中，从而大大减少了在下游任务上的可训练参数量。

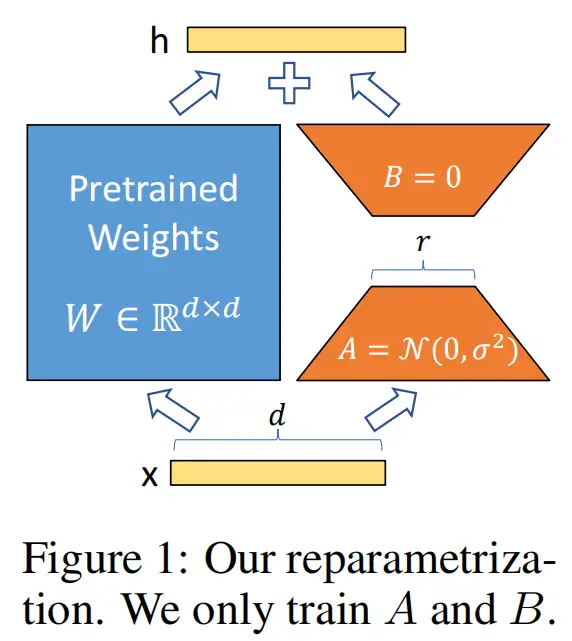
LoRA结构

We propose Low-Rank Adaptation(LoRA), which freezes the pre trained model weights and injects trainable rank decomposition matrices into each layer of the Transformer architecture, greatly reducing the number of trainable parameters for downstream tasks.

在推理时，对于使用LoRA的模型来说，可直接将原预训练模型权重与训练好的LoRA权重合并，因此在推理时不存在额外开销。

1.3 为什么要LoRA

背景

通常，冻结预训练模型权重，再额外插入可训练的权重是常规做法，例如Adapter。可训练的权重学习的就是微调数据的知识。

但它们的问题在于，不仅额外增加了参数，而且还改变了模型结构。

这会导致模型训练、推理的计算成本和内存占用急剧增加，尤其在模型参数需在多GPU上分布式推理时(这越来越常见)。

推理性能比较

动机

深度网络由大量Dense层构成，这些参数矩阵通常是满秩的。

相关工作表明，When adapting to a specific task, 训练学到的过度参数化的模型实际上存在于一个较低的内在维度上(高维数据实际是在低维子空间中)

We take inspiration from Li et al. (2018a); Aghajanyan et al. (2020) which show that the learned over-parametrized models in fact reside on a low intrinsic dimension.

低秩矩阵

LoRA就假设LLM在下游任务上微调得到的增量参数矩阵$\Delta \mathbf{W}$是低秩的(肯定不是满秩)，即存在冗余参数或高度相关的参数矩阵，但实际有效参数是更低维度的。

We hypothesize that the change in weights during model adaptation also has a low “intrinsic rank”, leading to our proposed Low-Rank Adaptation (LoRA) approach.

LoRA遂设想，对全参数微调的增量参数矩阵$\Delta \mathbf{W}$进行低秩分解近似表示(即对参数做降维)。

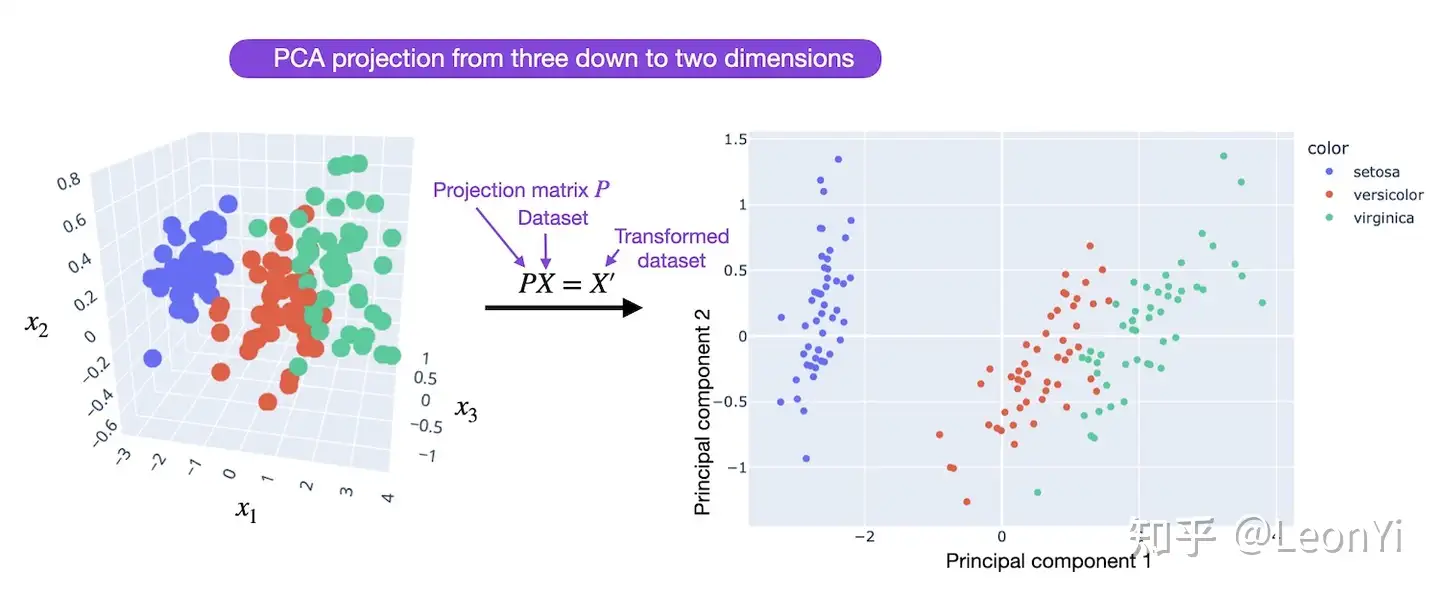
PCA降维示意图，源于https://lightning.ai/pages/community/tutorial/lora-llm/

这样训练$\Delta \mathbf{W}$的低秩分解近似参数矩阵，效果上相比其他PEFT方法不会打什么折扣，而且还能在推理时不增加额外开销。

LoRA allows us to train some dense layers in a neural network indirectly by optimizing rank decomposition matrices of the dense layers’ change during adaptation instead, while keeping the pre-trained weights frozen

LoRA的大体思路就是这样，具体的矩阵分解也是靠微调过程学习的。

接下来，介绍LoRA的具体方案。

1.4 LoRA实现

LoRA就是低秩矩阵适应，在冻结原有LLM参数时，用参数量更小的矩阵进行低秩近似训练。

LoRA原理

对于预训练权重矩阵$\mathbf{W}_{0} \in \mathbb{R}^{d \times d}$，LoRa限制了其更新方式，即将全参微调的增量参数矩阵$\Delta \mathbf{W}$表示为两个参数量更小的矩阵$\mathbf{B} $和$\mathbf{A}$的低秩近似：

$$\mathbf{W}_{0} + \Delta \mathbf{W} = \mathbf{W}_{0}+ \mathbf{B}\mathbf{A}$$

其中，$\mathbf{B}\in \mathbb{R}^{d \times r}$和$\mathbf{A}\in \mathbb{R}^{r \times d}$为LoRA低秩适应的权重矩阵，秩$r$远小于$d$。

此时，微调的参数量从原来$\Delta \mathbf{W}$的$d*d$，变成了$\mathbf{B}$ 和 $\mathbf{A}$的$2*r*d$。可知，$2*r*d << d*d$(有$2r << d$)

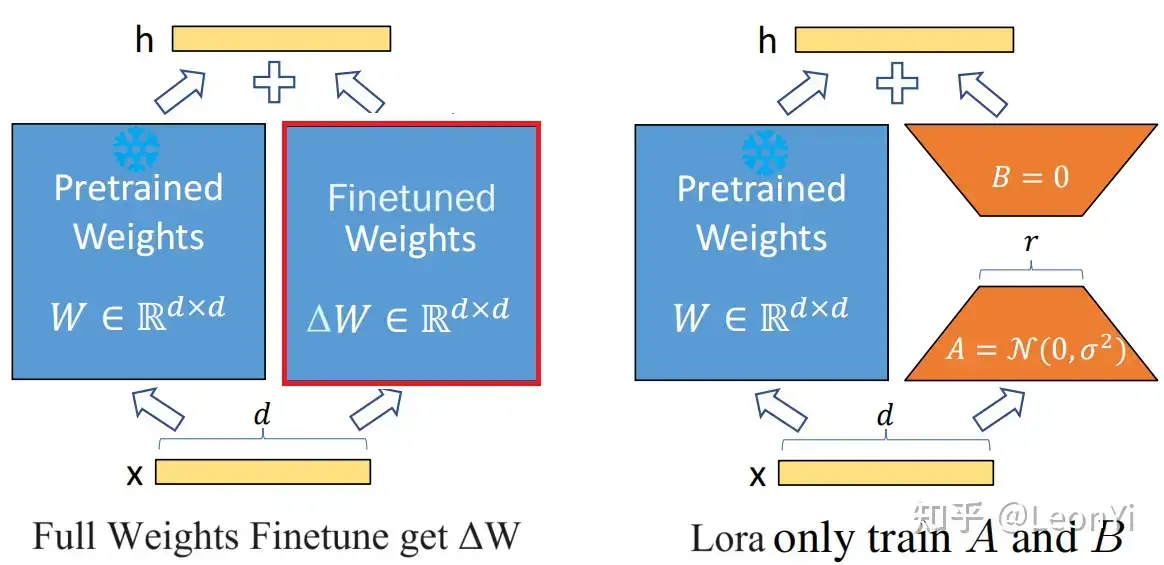
给定输入$\mathbf{x} \in \mathbb{R}^{d}$，添加LoRA后的输出$\mathbf{h} \in \mathbb{R}^{d}$：

$$\mathbf{h} = (\mathbf{W}_{0} + \Delta \mathbf{W} ) \mathbf{x} = \mathbf{W}_{0}\mathbf{x} + \mathbf{B}\mathbf{A} \mathbf{x}$$

这里，将$\Delta \mathbf{h}=\mathbf{B}\mathbf{A} \mathbf{x}$，便于后续求导计算。

在训练时，原始参数$\mathbf{W}_{0}$被冻结，意味着$\mathbf{W}_{0}$虽然会参与前向传播和反向传播，但是不会计算其对应梯度$\frac{\partial L}{\partial \mathbf{W}_0}$，更不会更新其参数。

在推理时，直接按上面的式子将$\mathbf{B}\mathbf{A}$合并到$\mathbf{W}_{0}$中，因此相比原始LLM不存在推理延时。

1.5 LoRA参数初始化

在开始训练时：

• 矩阵 $\mathbf{B}$ 通过高斯函数初始化，$b_i \sim N(0, {\sigma_b}^2)$

• 矩阵 $\mathbf{A}$ 为全零初始化，$a_i = 0$

这使得训练开始前，LoRA的旁路$\mathbf{B}\mathbf{A}=0$，那么微调就能从预训练权重$\mathbf{W}_{0}$开始。

这样就能和全参数微调时一样，能有相同的开始。

这个策略要求，至少$\mathbf{B}$ 和 $\mathbf{A}$中有一个被初始化为全0项。

但如果，全被初始化为0，$\mathbf{B}$ 和 $\mathbf{A}$就训不动了。因为，$\mathbf{B}$ 和 $\mathbf{A}$全0时，处于鞍点，两个权重的梯度也全为0声明：本文内容由网友自发贡献，不代表【wpsshop博客】立场，版权归原作者所有，本站不承担相应法律责任。如您发现有侵权的内容，请联系我们。转载请注明出处：https://www.wpsshop.cn/w/一键难忘520/article/detail/945345