代码随想录-动态规划

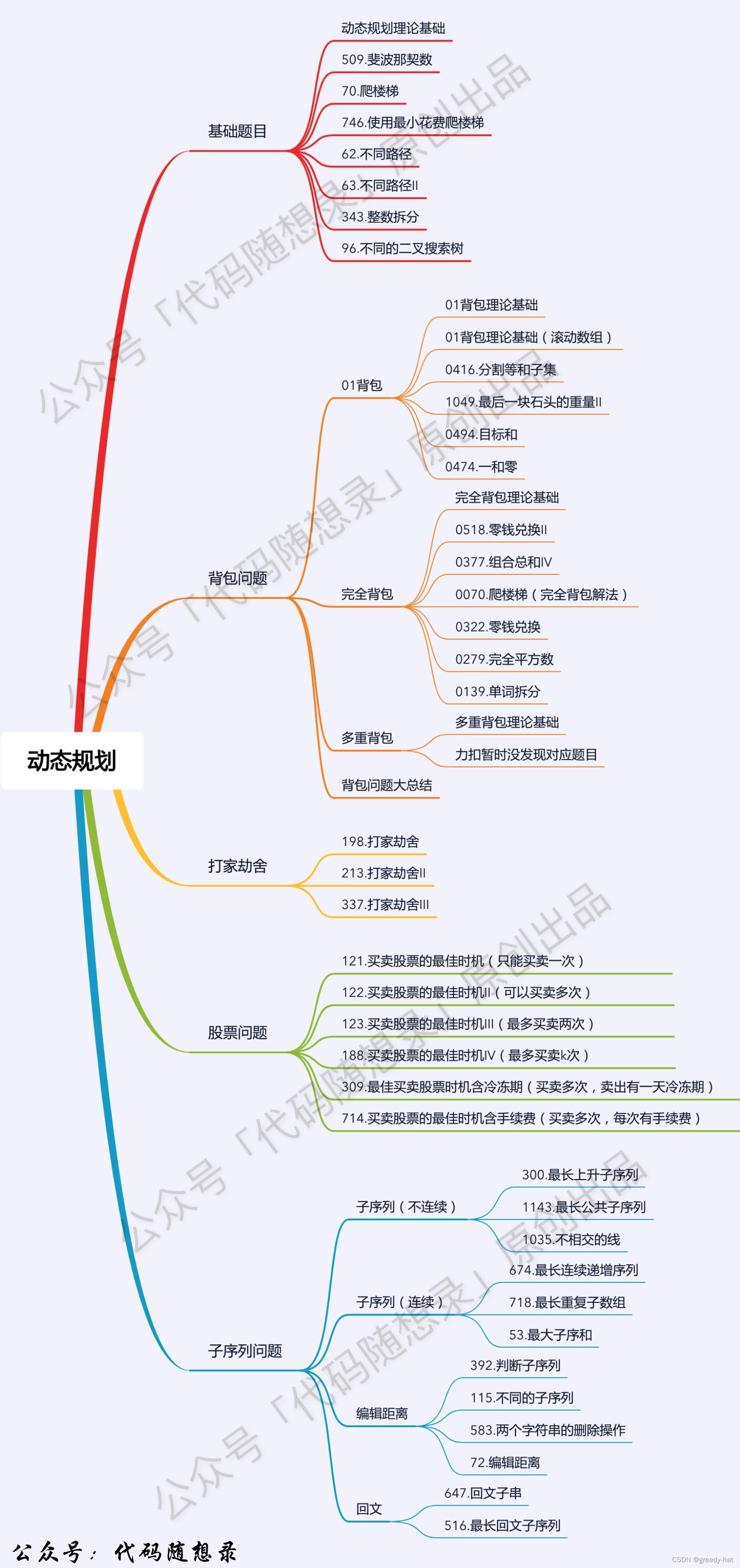
70. 爬楼梯

class Solution {
    public int climbStairs(int n) {
        int[] dp = new int[n+1];
        dp[0] = 1;
        dp[1] = 1;
        for(int i = 2;i <= n; i++){
            dp[i] = dp[i-1] + dp[i-2];
        }
        return dp[n];
    }
}
1
2
3
4
5
6
7
8
9
10
11

746.使用最小花费爬楼梯

class Solution {
    public int minCostClimbingStairs(int[] cost) {
        int len = cost.length;
        int[] dp = new int[len + 1];

        dp[0] = 0;
        dp[1] = 0;
        for (int i = 2; i <= len; i++) {
            dp[i] = Math.min((dp[i - 1] + cost[i - 1]), (dp[i - 2] + cost[i - 2]));
        }
        return dp[len];
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13

01背包

public class BagProblem {
    public static void main(String[] args) {
        int[] weight = {1,3,4};
        int[] value = {15,20,30};
        int bagSize = 4;
        testWeightBagProblem(weight,value,bagSize);
    }

    /**
     * 动态规划获得结果
     * @param weight  物品的重量
     * @param value   物品的价值
     * @param bagSize 背包的容量
     */
    public static void testWeightBagProblem(int[] weight, int[] value, int bagSize){

        // 创建dp数组
        int goods = weight.length;  // 获取物品的数量
        int[][] dp = new int[goods][bagSize + 1];

        // 初始化dp数组
        // 创建数组后，其中默认的值就是0
        for (int j = weight[0]; j <= bagSize; j++) {
            dp[0][j] = value[0];
        }

        // 填充dp数组
        for (int i = 1; i < weight.length; i++) {
            for (int j = 1; j <= bagSize; j++) {
                if (j < weight[i]) {
                    /**
                     * 当前背包的容量都没有当前物品i大的时候，是不放物品i的
                     * 那么前i-1个物品能放下的最大价值就是当前情况的最大价值
                     */
                    dp[i][j] = dp[i-1][j];
                } else {
                    /**
                     * 当前背包的容量可以放下物品i
                     * 那么此时分两种情况：
                     *    1、不放物品i
                     *    2、放物品i
                     * 比较这两种情况下，哪种背包中物品的最大价值最大
                     */
                    dp[i][j] = Math.max(dp[i-1][j] , dp[i-1][j-weight[i]] + value[i]);
                }
            }
        }

        // 打印dp数组
        for (int i = 0; i < goods; i++) {
            for (int j = 0; j <= bagSize; j++) {
                System.out.print(dp[i][j] + "\t");
            }
            System.out.println("\n");
        }
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57

01背包-滚动数组

public static void main(String[] args) {
    int[] weight = {1, 3, 4};
    int[] value = {15, 20, 30};
    int bagWight = 4;
    testWeightBagProblem(weight, value, bagWight);
}

public static void testWeightBagProblem(int[] weight, int[] value, int bagWeight){
    int wLen = weight.length;
    //定义dp数组：dp[j]表示背包容量为j时，能获得的最大价值
    int[] dp = new int[bagWeight + 1];
    //遍历顺序：先遍历物品，再遍历背包容量
    for (int i = 0; i < wLen; i++){
        for (int j = bagWeight; j >= weight[i]; j--){
            dp[j] = Math.max(dp[j], dp[j - weight[i]] + value[i]);
        }
    }
    //打印dp数组
    for (int j = 0; j <= bagWeight; j++){
        System.out.print(dp[j] + " ");
    }
 }
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22

416. 分割等和子集

class Solution {
    public boolean canPartition(int[] nums) {
        if (nums == null || nums.length == 0) {
            return false;
        }
        int len = nums.length;
        int sum = 0;
        for (int num : nums) {
            sum += num;
        }
        if (sum % 2 != 0)
            return false;
        int target = sum / 2;
        int[] dp = new int[target + 1];
        for (int i = 0; i < len; i++) {
            for (int j = target; j >= nums[i]; j--) {
                dp[j] = Math.max(dp[j], dp[j - nums[i]] + nums[i]);
            }

            if (dp[target] == target) {
                return true;
            }
        }
        return dp[target] == target;
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26

1049. 最后一块石头的重量 II

class Solution {
    public int lastStoneWeightII(int[] stones) {
        int len = stones.length;
        int sum = 0;
        for (int stone : stones) {
            sum += stone;
        }
        int target = sum / 2;
        int[] dp = new int[target + 1];
        for (int i = 0; i < len; i++) {
            for (int j = target; j >= stones[i]; j--) {
                dp[j] = Math.max(dp[j], dp[j - stones[i]] + stones[i]);
            }
        }
        return sum - dp[target] - dp[target];
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17

494. 目标和

class Solution {
    public int findTargetSumWays(int[] nums, int target) {
        int sum = 0;
        for (int num : nums) {
            sum += num;
        }
        int diff = sum - target;
        if (diff < 0 || diff % 2 != 0) {
            return 0;
        }
        int neg = diff / 2;
        int[] dp = new int[neg + 1];
        dp[0] = 1;
        for (int num : nums) {
            for (int j = neg; j >= num; j--) {
                dp[j] += dp[j - num];
            }
        }
        return dp[neg];
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21

322. 零钱兑换

class Solution {
    public int coinChange(int[] coins, int amount) {
        int[] dp = new int[amount + 1];
        Arrays.fill(dp, amount + 1);
        dp[0] = 0;
        for (int i = 1; i <= amount; i++) {
            for (int coin : coins) {
                if (i < coin) {
                    continue;
                }
                dp[i] = Math.min(dp[i], dp[i - coin]);
            }
            dp[i] += 1;
        }
        return dp[amount] > amount ? -1 : dp[amount];
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17

class Solution {
    public int coinChange(int[] coins, int amount) {
        int[] dp = new int[amount + 1];
        Arrays.fill(dp, amount + 1);
        dp[0] = 0;
        for (int i = 1; i <= amount; i++) {
            for (int coin : coins) {
                if (i < coin) {
                    continue;
                }
                dp[i] = Math.min(dp[i], dp[i - coin] + 1);
            }
        }
        return (dp[amount] == amount + 1) ? -1 : dp[amount];
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16

279. 完全平方数

class Solution {
    public int numSquares(int n) {
        int[] dp = new int[n + 1];
        for(int i = 1; i <= n;i++) {
            int minn = Integer.MAX_VALUE;
            for(int j = 1; j * j <= i; j++){
                minn = Math.min(minn, dp[i - j * j]);
            }
            dp[i] = minn + 1;
        }
        return dp[n];
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13

748. 打家劫舍

class Solution {
    public int rob(int[] nums) {
        if (nums.length == 0) {
            return 0;
        }

        int len = nums.length;
        int[] dp = new int[len+1];
        dp[0] = 0;
        dp[1] = nums[0];
        for(int i = 2; i <= len; i++){
            dp[i] = Math.max(dp[i-1], dp[i-2] + nums[i-1]);
        }
        return dp[len];
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16