- 1Android应用程序和其设计思想--转载----做记录_安卓app系统设计思想
- 2【chrome】 谷歌小技巧 谷歌浏览器 自带 滚动截图 chrome滚动截屏(全屏截图)
- 3【服务器】安卓手机使用Termux搭建web服务_termux无法安装apache2-dev
- 4基于Python的餐厅点餐系统-订餐食堂预约Python爬虫安装数据分析与可视化计算机毕业设计_预约爬虫
- 5如何使用Edge Copilot
- 6PostgreSQL(三)pgpool管理PostgreSQL集群下主机宕机后的主从切换_pg 启动后 status down
- 7python 多线程与线程池_python的线程池和 thread有什么区别
- 8openwrt信号弱掉线_openwrt路由器宽带频繁掉线解决方案
- 92023年10款超好用的Mac软件推荐(一)
- 10常用 FFmpeg 命令_ffmpeg命令大全
2023年亚太杯APMCM数学建模大赛ABC题辅导及组队
赞
踩
2023年亚太杯APMCM数学建模大赛
ABC题
一元线性回归分析类
回归分析(Regression Analysis)是确定两种或两种以上变量间相互依赖的定量关系的一种统计分析方法。
– 按涉及变量个数划分
• 一元回归分析
• 多元回归分析
– 按自变量和因变量之间关系划分
• 线性回归分析
• 非线性回归分析
回归分析主要解决两个问题
➢ 一是确定几个变量之间是否存在相关关系,如果存在,找出它们之间适当的数学表达式。
➢ 二是根据一个或几个变量的值,预测或控制另一个或几个变量的值。
变量间的关系
– 确定性关系
确定性关系是指当一些变量的值确定以后另一些变量的值也随之完全确定的关系,这些变量间的关系完全是已知的,变量之间的关系可以用函数关系来表示。
• 圆的面积与半径之间的关系 。
• 如:价格不变时,某商品的销售收入与销售量的关系。
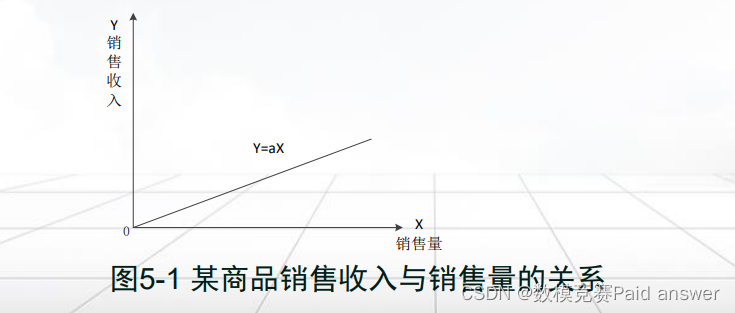
变量间的关系
– 非确定性关系
非确定性关系是指变量之间有一定的依赖关系,变量之间虽然相互影响和相互制约,但由于受到无法预计和控制的因素的影响,使得变量间的关系呈现不确定性,当一些变量的值确定以后,另一些变量值虽然随之变化,却不能完全确定,这时变量间的关系就不可以精确地用函数来表示,即不能由一个或若干变量的值精确地确定另一变量的值。
• 子女的身高与父亲及母亲的身高之间的关系。
• 农田粮食的产量与施肥量之间的关系。
• 商品的销售量与广告费之间的关系。
回归分析的步骤
• 确定变量。寻找与预测目标的相关影响因素,即自变量,并从中选出主要的影响因素。
• 建立预测模型。依据自变量和因变量的历史统计资料进行计算,在此基础上建立回归分析预测模型。
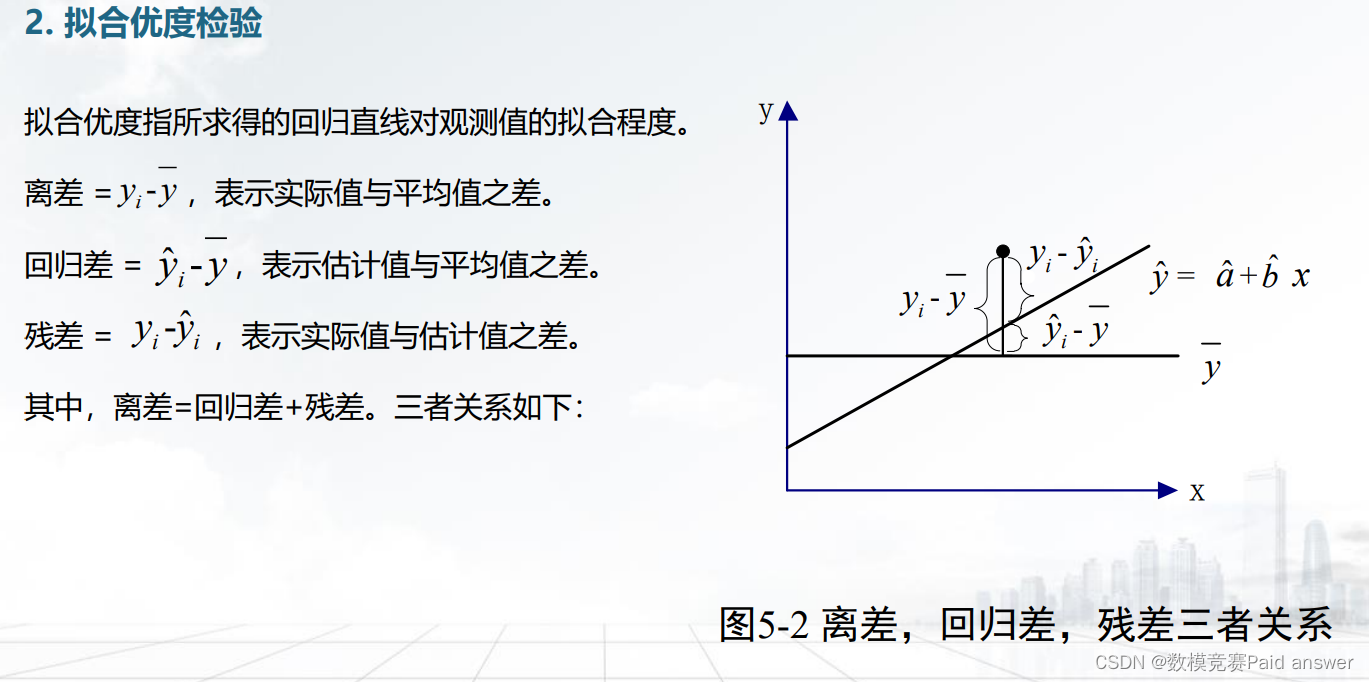
• 进行相关分析。作为自变量的因素与作为因变量的预测对象是否有关,相关程度如何,以及判断这种相关程度的把握性多大,就成为进行回归分析必须要解决的问题。进行相关分析,一般要求出相关关系,以相关系数的大小来判断自变量和因变量的相关程度。
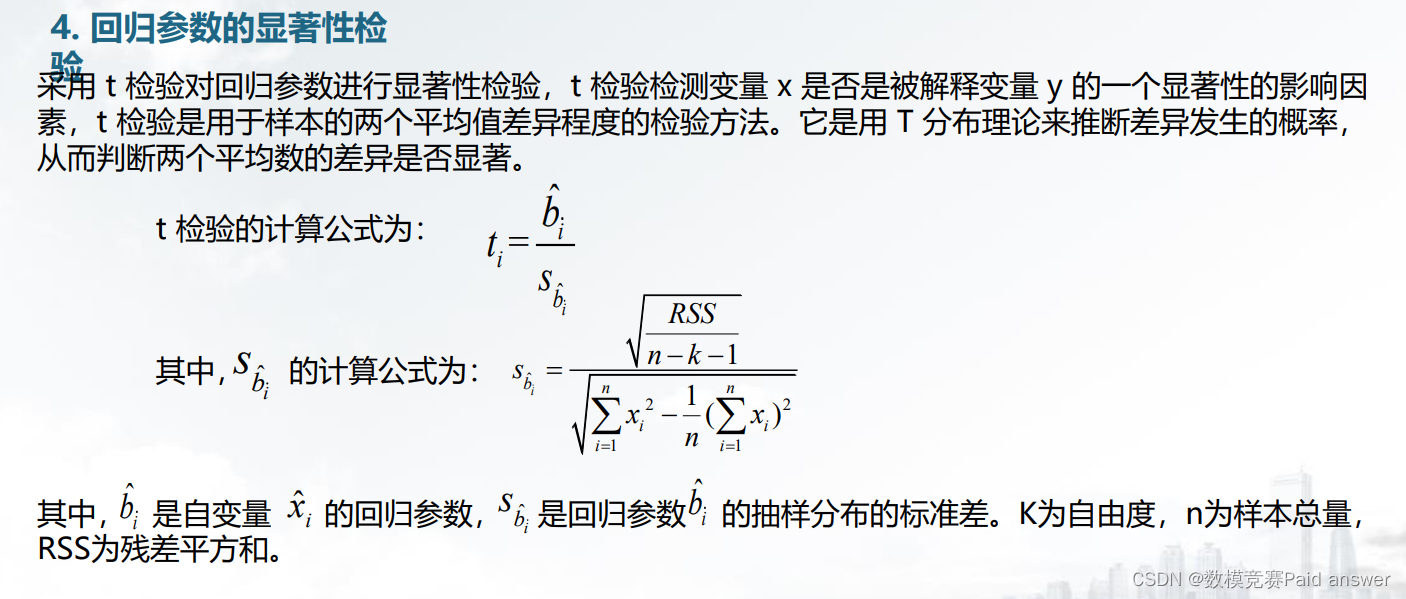
• 计算预测误差。回归预测模型是否可用于实际预测,取决于对回归预测模型的检验和对预测误差的计算。
• 确定预测值。利用回归预测模型计算预测值,并对预测值进行综合分析,确定最后的预测值。




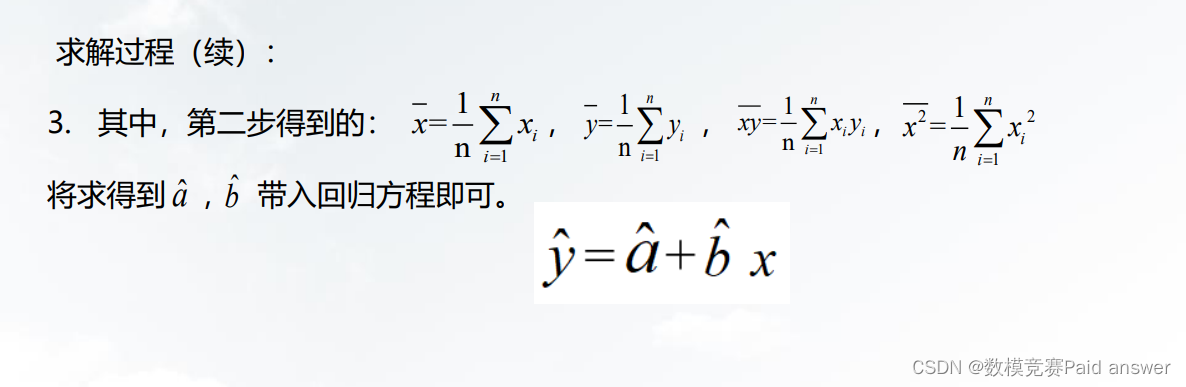



想组队的请见下方“ 只会建模 QQ名片” 点击QQ名片即可
序号 x1 年份 水路货运量y
1 1991 1659
2 1992 1989
3 1993 2195
4 1994 2255
5 1995 2329
6 1996 2375
7 1997 2364
8 1998 2354
9 1999 2418
10 2000 2534
11 2001 2568
12 2002 2835
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
import matplotlib.pyplot as plt from sklearn.linear_model import LinearRegression # 设置中文字体 plt.rcParams['font.sans-serif'] = ['SimHei'] # 读取Excel文件 data = pd.read_excel('E:\\File\\class\\数据挖掘\\test1.xlsx') x = data[['年份']] y = data['水路货运量y'] # 训练模型 model = LinearRegression() model.fit(x, y) # 预测值 x_new = [[2004]] y_pred = model.predict(x_new) print("预测值为:", y_pred[0]) # 绘制图像 plt.scatter(x, y) plt.plot(x, model.predict(x), color='r') plt.xlabel('年份') plt.ylabel('水路货运量y') plt.title('一元线性回归预测模型案例') plt.show()
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22




