蓝桥杯C_C++/Java程序设计常用算法&技巧总结_蓝桥杯算法训练java

精度处理

例如：我们想要程序判别 0.1+0.2 == 0.3

1.比较法

取等式差值的绝对值小于某一个特别小的数，若差值小于特别小的数则条件成立，反之。

if( fabs(0.2 + 0.1 -0.3) <= 1E-10 ) //一般1的负10次方够用了
        cout<<"true"<<endl;     
    else 
        cout<<"false"<<endl;
1
2
3
4

2.整型比较

由于计算机对于整形的运算绝对精准，所以把浮点运算化整形运算的做法是我们常用的。
将等式两边分别乘以10

if(1 + 2 == 3)
        cout<<"true"<<endl;     
    else 
        cout<<"false"<<endl;
1
2
3
4

最大公约数&最小公倍数

最大公约数

1.短除法

/**短除法*/
int enum_max_common_divisor(int a,int b)//大的值为b，枚举法 
{
    for(int i=a;i>=1;i--)   //当两个数互质时，则最大公约数为I 
        if(a%i==0 && b%i==0)        
            return i;   
} 
1
2
3
4
5
6
7

2.辗转除法

/**辗转除法*/ 
int max_common_divisor(int a,int b)//递归辗转除法,优点：a,b可以任意值输入 
{ 
    if(a==0) return b;
     return max_common_divisor(b%a,a);
}
1
2
3
4
5
6

最小公倍数

最小公倍数 = a*b /最大公约数

/*最小公倍数= a*b /最大公约数 
  a= ka*i  b= kb*i    a*b = ka*kb*i*i    */ 
int min_common_multiple(int a,int b)
{
    return a*b/max_common_divisor(a,b);
}  
1
2
3
4
5
6

递归

递归的特点：

1）递归就是方法里调用自身。

2）在使用递增归策略时，必须有一个明确的递归结束条件，称为递归出口。

3）递归算法解题通常显得很简洁，但递归算法解题的运行效率较低。所以一般不提倡用递归算法设计程序。

4）在递归调用的过程当中系统为每一层的返回点、局部量等开辟了栈来存储。递归次数过多容易造成栈溢出等，所以一般不提倡用递归算法设计程序。

构造递归主要是构造出口（output）和移动变量(moveParameter)。

例子

1.斐波纳契数列（Fibonacci Sequence）

在数学上，斐波纳契数列以如下被以递归的方法定义：F1=1,F2=1,Fn=F（n-1）+F（n-2）（n>2,n∈N*））

int fib(int index)
{
       if(index==1||index==2)//出口
   {  
          return 1;  
    }
    else
    {  
          return fib(index-1)+fib(index-2);  
    }
}
1
2
3
4
5
6
7
8
9
10
11
12

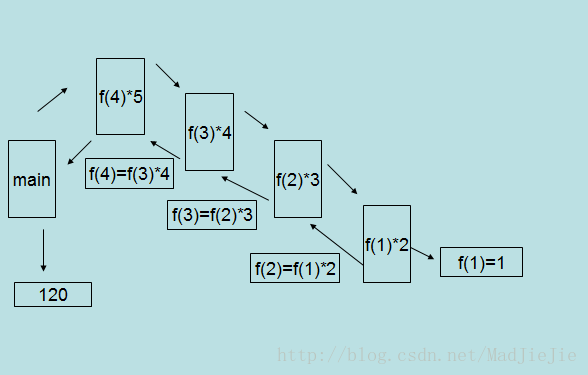
2.N的阶层

int factorial(int index)
{
    if(index==1)
    {  
            return 1;  
    }
    else
    {  
            return factorial(index-1)*index;  
    } 
}
1
2
3
4
5
6
7
8
9
10
11

递归算法转换成为非递归算法

将递归算法转换为非递归算法有两种方法，一种是直接求值，不需要回溯；另一种是不能直接求值，需要回溯。前者使用一些变量保存中间结果，称为直接转换法；后者使用栈保存中间结果，称为间接转换法，下面分别讨论这两种方法。

1. 直接转换法
   　　直接转换法通常用来消除尾递归和单向递归，将递归结构用循环结构来替代。尾递归是指在递归算法中，递归调用语句只有一个，而且是处在算法的最后。例如求阶乘的递归算法：

　  long fact(int n)
　　{
    　　if (n==0) 
        　　return 1;
    　　else 
        　　return n*fact(n-1);
　　}
1
2
3
4
5
6
7

　　当递归调用返回时，是返回到上一层递归调用的下一条语句，而这个返回位置正好是算法的结束处，所以
，不必利用栈来保存返回信息。对于尾递归形式的递归算法，可以利用循环结构来替代。例如求阶乘的递归算法
可以写成如下循环结构的非递归算法：

    long fact(int n)
　　{
    　　int s=1;
    　　for (int i=1; i<n;i++)
        　　s=s*i; //用s保存中间结果
    　　return s;
　　}
1
2
3
4
5
6
7

　　单向递归是指递归算法中虽然有多处递归调用语句，但各递归调用语句的参数之间没有关系，并且这些递归
调用语句都处在递归算法的最后。显然，尾递归是单向递归的特例。例如求斐波那契数列的递归算法如下：

    int f(int n)
　　{
    　　if (n= =1 | | n= =0) 
    　　return 1;
    　　else 
    　　return f(n-1)+f(n-2);
　　}
1
2
3
4
5
6
7

　　对于单向递归，可以设置一些变量保存中间结构，将递归结构用循环结构来替代。例如求斐波那契数列的算
法中用s1和s2保存中间的计算结果，非递归函数如下：

    int f(int n)
    {
    　　int a[n+2];
        a[1]=1,a[2]=1;
    　　for(i=3;i<=n;i++)
        {
            a[i] = a[i-1] + a[i-2]; 
        }
    　　return a[n];
    }
1
2
3
4
5
6
7
8
9
10

递归经典竞赛应用

李白打酒

话说大诗人李白，一生好饮。幸好他从不开车。

一天，他提着酒壶，从家里出来，酒壶中有酒2斗。他边走边唱：

逢店加一倍，遇花喝一斗。

这一路上，他一共遇到店5次，遇到花10次，已知最后一次遇到的是花，他正好把酒喝光了。

请你计算李白遇到店和花的次序，可以把遇店记为a，遇花记为b。

int total=0;  
int a(int s,int f,int d)
{  
    if(s>0) //当店大于0，就行搜索   
        a(s-1,f,d*2); //return a(s-1,f,d*2); 

    if(f>1) //花大于1，进行搜索   
        a(s,f-1,d-1);  

    if(s==0 && f==1 && d==1) //保证最后一次遇见的是花 此时还剩下1斗酒   
        total++;  

    return total;  
}  
int main()
{  
    printf("%d",a(5,10,2)); //初始化为最初有 5个店 10个花 2斗酒   
    return 0;  
}  
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19

第39级台阶

#include <iostream>
using namespace std;
#include <cstdio>
#include <cstdlib>
#include <cmath>
#include <algorithm> 

#define LEFT false
#define RIGHT true

static int total;
void f(int step,bool flag)
{
    if(step>39)//出口
        return ;

    if(flag==RIGHT && step==39)//判断条件是否符合
    {
        total ++;
        return;
    }
    f(step+1,!flag);//遍历迈一步的方式
    f(step+2,!flag);//遍历迈两步的方式
}

int main()
{
    f(1,LEFT); //第一步迈一步 
    f(2,LEFT);//第一步迈两步 
    cout<<total;
    return 0;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32

返回累加性解法

#define LEFT false
 #define RIGHT true

static int total;

long f(int step,bool flag)
{
     if(step == 1)//判断第一步左脚是一步
     {  
         if(flag == RIGHT)  
            return 1;  
         else 
            return 0;  
     }  
     else if(step == 2)//判断第一步左脚是两步，必定最后一步为右脚
     {  
        return 1;  
     }  

    if(flag==RIGHT && step==0)
    {
        return 1;
    }
    else if(step<=0)
    {
        return 0;
    }

    return f2(step-1,!flag)+f2(step-2,!flag);
}

int main()
{
    cout<<f(39,LEFT)<<endl;
    cout<<total;

    return 0;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38

DFS

回溯型DFS

字符串全排列

DFS构建步骤

1.设定step出口变量，在出口处拦截适宜的数据；

2.构造原数据数组old && 移动数据数组a[]；

3.for循环处对数据进行排列置换

4.for循环步骤 ：判断使用标志位i下标的数据为未被使用，条件成立->置该数组下标使用标志->置换数据a[step] = old[i]，注意前者是出口移动变量，后者是i变量->递归dfs(step+1),使函数步移->回溯，置该标志位数组下标未使用标志

#define ARRAY_LENGTH 4
#define NOT_USED 0
#define USED 1

char old[ARRAY_LENGTH] = {'a','b','c','d'};
char a[ARRAY_LENGTH];
int useFlag[ARRAY_LENGTH];
void dfs(int step)
{
    if(step >= ARRAY_LENGTH)    //出口，过滤数据找出结果 
    {
        for(int i=0;i<ARRAY_LENGTH;i++)
        {
            cout<<a[i]<<" ";
        }
        cout<<endl;
        return ;
    }

    for(int i=0;i<ARRAY_LENGTH;i++)
    {
        if( useFlag[i] == NOT_USED) //判断该下标的标志位是否被使用 
        {
            useFlag[i] = USED;      //置使用标志 
            a[step] = old[i];       //置换数据，排列数组 
            dfs(step+1);            //递归    
            useFlag[i] = NOT_USED; //回溯 
        }
    }

}

int main(void)
{   
    memset(useFlag,NOT_USED,sizeof(useFlag));
    dfs(0);     
    return 0;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38

从for循环角度理解不回溯型DFS

小明与其他3人玩牌。
一副扑克牌（去掉大小王牌，共52张），均匀发给4个人，每个人13张。
这时，小明脑子里突然冒出一个问题：
如果不考虑花色，只考虑点数，也不考虑自己得到的牌的先后顺序，自己手里能拿到的初始牌型组合一共有多少种呢？

int main()
{
    int sum =0;
    int total=0;
    int a[14];
    for( a[1]=0;a[1]<=4;a[1]++)     //1 
        for( a[2]=0;a[2]<=4;a[2]++) //2 
            for( a[3]=0;a[3]<=4;a[3]++) //3 
                for( a[4]=0;a[4]<=4;a[4]++) //4 
                    for( a[5]=0;a[5]<=4;a[5]++) //5 
                        for( a[6]=0;a[6]<=4;a[6]++) //6 
                            for( a[7]=0;a[7]<=4;a[7]++) //7 
                                for( a[8]=0;a[8]<=4;a[8]++) //8 
                                    for( a[9]=0;a[9]<=4;a[9]++) //9 
                                        for( a[10]=0;a[10]<=4;a[10]++)  //10 
                                            for( a[11]=0;a[11]<=4;a[11]++)  //11 
                                                for( a[12]=0;a[12]<=4;a[12]++)  //12 
                                                    for( a[13]=0;a[13]<=4;a[13]++)      //13
            {
                for(int i=1;i<=13;i++)
                {
                    sum += a[i];
                }
                if(sum == 13)
                {
                    total++;
                }
                sum=0;
            }   

    cout<<total;                                     

    return 0;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34

/**
parameter： n:步移 ； cartNum:手上的牌数量 ； 这两个变量为控制出口变量。  
*/ 
void dfs(int n,int cartNum)  
{

    if(n>14)        //出口1：抽牌的次数(13次)越界 相当于for循环阶数:13阶 
    {
        return;
    }

    if(cartNum>=13)     //出口2：牌数量越界 
    {
        if(cartNum==13) //截取条件成立的结果 
            sum++;
        return;
    } 
    else            //相当于for循环中的条件int a=0~a<=4; 
    {
        dfs(n+1,cartNum);       //没有该类的牌 
        dfs(n+1,cartNum+1);     //有一张该类的牌  
        dfs(n+1,cartNum+2);     //有两张该类的牌 
        dfs(n+1,cartNum+3);     //有三张该类的牌 
        dfs(n+1,cartNum+4);     //有四张该类的牌 
    }

} 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27

竞赛应用

带分数

100 可以表示为带分数的形式：100 = 3 + 69258 / 714

还可以表示为：100 = 82 + 3546 / 197

注意特征：带分数中，数字1~9分别出现且只出现一次（不包含0）。

类似这样的带分数，100 有 11 种表示法。
1
2
3
4
5
6
7

题目要求：
从标准输入读入一个正整数N (N<1000*1000)
程序输出该数字用数码1~9不重复不遗漏地组成带分数表示的全部种数。
注意：不要求输出每个表示，只统计有多少表示法！

例如：
用户输入：
100
程序输出：
11

再例如：
用户输入：
105
程序输出：
6

资源约定：
峰值内存消耗 < 64M
CPU消耗 < 3000ms

请严格按要求输出，不要画蛇添足地打印类似：“请您输入…” 的多余内容。

所有代码放在同一个源文件中，调试通过后，拷贝提交该源码。

注意: main函数需要返回0
注意: 只使用ANSI C/ANSI C++ 标准，不要调用依赖于编译环境或操作系统的特殊函数。
注意: 所有依赖的函数必须明确地在源文件中 #include ， 不能通过工程设置而省略常用头文件。

提交时，注意选择所期望的编译器类型。

解法一

dfs N=A+B/C⇨B=(N-A)*C。根据公式，只需要求A和C就可以进行判断了。A的范围是1~N，但是这些数中有很多是无用的（如：11，101……）。我们只选有用的数，用vis数组标记1~9中已经用过的数字，避免做不必要的搜索。

#include <iostream>
using namespace std;
#include<algorithm>
#include <cstdio>
#include <cstdlib> 
#include <cstring>


int ans = 0;        //
bool vis[10];
int n; int A = 0, C = 0;
int lenN; int ALEN = 0, CLEN = 0;
bool judge() {
    bool vistemp[10];
    memcpy(vistemp, vis, sizeof(vis));
    int t = (n - A)*C; int BLEN = 0;
    while (t) {
        if (vistemp[t % 10]) return false;
        vistemp[t % 10] = 1;
        BLEN++;
        t /= 10;
    }
    return BLEN+ALEN+CLEN==9;
}

void dfs(int flag) 
{
    if (flag == 2)
    {
        if (judge()) ans++;
        return;
    }
    for (int i = 1; i <= 9; i++) 
    {
        if (vis[i]) continue;
        vis[i] = 1;
        if (flag == 1) 
        {
            A *= 10; A += i; ALEN += 1;
            if (A<=n) 
            {
                dfs(1);
                dfs(3);
                ALEN -= 1; A /= 10;
            }
            else if (A > n) 
            {
                ALEN -= 1; A /= 10;
                vis[i] = 0;
                break;
            }
        }
        else if (flag == 3) {
            if (CLEN < (9 - ALEN) / 2) 
            {
                C *= 10; C += i; CLEN++;
                dfs(2);
                dfs(3);
                C /= 10; CLEN--;
            }
            else { vis[i] = 0; break; }
        }
        vis[i] = 0;
    }
}
int main() {
    cin >> n;
    int temp = n;
    lenN = 0;
    while (temp) { lenN++; temp /= 10; }
    memset(vis, 0, sizeof(vis));
    vis[0] = 1;
    dfs(1);
    cout << ans << endl;
    return 0;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77

地宫取宝

X 国王有一个地宫宝库。是 n x m 个格子的矩阵。每个格子放一件宝贝。每个宝贝贴着价值标签。

地宫的入口在左上角，出口在右下角。

小明被带到地宫的入口，国王要求他只能向右或向下行走。

走过某个格子时，如果那个格子中的宝贝价值比小明手中任意宝贝价值都大，小明就可以拿起它（当然，也可以不拿）。

当小明走到出口时，如果他手中的宝贝恰好是k件，则这些宝贝就可以送给小明。

请你帮小明算一算，在给定的局面下，他有多少种不同的行动方案能获得这k件宝贝。
1
2
3
4
5
6
7
8
9
10
11

【数据格式】

输入一行3个整数，用空格分开：n m k (1<=n,m<=50, 1<=k<=12)

接下来有 n 行数据，每行有 m 个整数 Ci (0<=Ci<=12)代表这个格子上的宝物的价值

要求输出一个整数，表示正好取k个宝贝的行动方案数。
该数字可能很大，输出它对 1000000007 取模的结果。
1
2
3
4
5
6

例如，输入：
2 2 2
1 2
2 1
程序应该输出：
2

再例如，输入：
2 3 2
1 2 3
2 1 5
程序应该输出：
14

资源约定：
峰值内存消耗 < 256M
CPU消耗 < 1000ms

请严格按要求输出，不要画蛇添足地打印类似：“请您输入…” 的多余内容。

所有代码放在同一个源文件中，调试通过后，拷贝提交该源码。

注意: main函数需要返回0
注意: 只使用ANSI C/ANSI C++ 标准，不要调用依赖于编译环境或操作系统的特殊函数。
注意: 所有依赖的函数必须明确地在源文件中 #include ， 不能通过工程设置而省略常用头文件。

提交时，注意选择所期望的编译器类型。

解法一

4维的记忆化DFS,题目要求只能下或右走，从左上角走到右下角，记录下每个坐标下的数量和最大宝贝价值下的走的情况

#include<stdio.h>
#include<string.h>
#include<string>
#include<algorithm>
#include<math.h>
#include<iostream>
#include<time.h>

#define mod  1000000007
using namespace std;

int n,m,k;
int c[55][55];
int dp[55][55][101][15];
int dfs(int x,int y,int mun,int v)  //x,y表示坐标，mun表示手中宝贝的数量，V表示手中的最大宝贝的价值
{
    if(dp[x][y][mun][v]!=-1)//记录了经过 此坐标此数量此价值下的所有走法，
        return dp[x][y][mun][v];//所以直接返回，后面的无需走了

    if(x==n-1&&y==m-1)
    {
        if(mun==k||(mun==k-1&&c[x][y]>v))//符合要求的算一种
            return dp[x][y][mun][v]=1;
        else
        {
          return dp[x][y][mun][v]=0;//不符合       
        }
    }

    int t=0;

    if(y+1<m))//x<n-1
    {
        if(c[x][y]>v)//选择拿起宝贝
        {
            t=(t+dfs(x,y+1,mun+1,c[x][y]))%mod;     
        }

        t=(t+dfs(x,y+1,mun,v))%mod;//选择不拿 
    }

    if(x+1<n)//x<n-1
    {
        if(c[x][y]>v)
        {
            t=(t+dfs(x+1,y,mun+1,c[x][y]))%mod;     
        }

        t=(t+dfs(x+1,y,mun,v))%mod;
    }

    return dp[x][y][mun][v]=t%mod;//由右和下返回的值记录于此坐标下，下次路过此时 
    //不再递归 
}
int main()
{
    memset(dp,-1,sizeof(dp));   //标志 
    scanf("%d%d%d",&n,&m,&k);

    for(int i=0;i<n;i++)
        for(int j=0;j<m;j++)
        {
            scanf("%d",&c[i][j]);
            c[i][j]++;//为什么加1,因为有的宝贝价值问0，会出现比较错误
        }

    printf("%d\n",dfs(0,0,0,0));
    return 0;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70

贪心

动态规划

常用函数

C常用头文件

标准输入输出

#include < cstdio >

scanf()

printf()

标准库

#include < cstdlib >

qsort()

数学库

#include < cmath>

字符串库

#include < cstring >

memset(array_first_address, NUM, sizeof(array));

C常用头文件

标准输入输出

#include < iostream >

using namespace std;

cin>>

cout<<

算法库

#include < algorithm >

next_permutation(array_first_address , array_first_address+length);

sort(array_first_address , array_first_address+length);

其他技巧

康托展开式公式:

X=an*(n-1)!+an-1*(n-2)!+…+ai*(i-1)!+…+a2*1!+a1*0!

这个式子是由1到n这n个数组成的全排列，共n!个，按每个全排列组成的数从小到大进行排列，并对每个序列进行编号（从0开始）,并记为X。

比如说1到4组成的全排列中，长度为4，1234对应编号0，1243对应编号1

那a1,a2,a3,a4是什么意思呢？==>>

对1到4的全排列中，我们来考察3214，则

a4={3在集合(3,2,1,4)中是第几大的元素}=2

a3={2在集合(2,1,4)中是第几大的元素}=1

a2={1在集合(1,4)中是第几大的元素}=0

a1=0（最后只剩下一项）

则X=2*3!+1*2!+0*1!+0*0!=14，即3214对应的编号为14。

因此，此题用康托展开式就可以出来了，将abcd…写成1，2，3，4…就行了。

long long a[ 17 ];

long long fun(long long n)  //求阶乘
{
    long long s = 1;
    for(int i = 1;i<=n;i++)
        s*=i;
    return s;
}


int main()
{
        long long t;
        int f[] = {2,3,11,6,17,12,1,10,8,5,13,7,9,15,4,14,16};
        long long sum = 0;

        a[0] = 1;
        for(int i=1;i<17;i++)
        {
            a[i] = a[i-1]*i;
        }       

        for(int i = 0;i<16;i++)
        {
            t = 0;
            for(int j = i+1;j<17;j++)
            {
                if(f[j]<f[i])
                {
                    t++;
                }
            }
           sum += (t)*a[17-1-i];        //康托展开式公式  
        }

        printf("%lld",sum);

        return 0;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40