深入理解Transformer，兼谈MHSA（多头自注意力）、Cross-Attention（交叉注意力）、LayerNorm、FFN、位置编码_mhsa注意力机制

Attention Is All You Need——集中一下注意力

• Transformer其实不是完全的Self-Attention（SA，自注意力）结构，还带有Cross-Attention（CA，交叉注意力）、残差连接、LayerNorm、类似1维卷积的Position-wise Feed-Forward Networks（FFN）、MLP和Positional Encoding（位置编码）等
• 本文涵盖Transformer所采用的MHSA（多头自注意力）、LayerNorm、FFN、位置编码
• 对1维卷积的详解请参考深入理解TDNN（Time Delay Neural Network）——兼谈x-vector网络结构
• 对SA的Q、K、V运算的详解请参考深入理解Self-attention（自注意力机制）

Transformer的训练和推理

• 序列任务有三种：
  • 序列转录：输入序列长度为N，输出序列长度为M，例如机器翻译
  • 序列标注：输入序列长度为N，输出序列长度也为N，例如词性标注
  • 序列总结：输入序列长度为N，输出为分类结果，例如声纹识别
• 前两个序列任务，常用Transformer进行统一建模，Transformer是一种Encoder-Decoder结构。在Transformer中：
• 推理时
  • Encoder负责将输入$(x_1,x_2,...,x_n)$，编码成隐藏单元（Hidden Unit）$(z_1,z_2,...,z_n)$，Decoder根据隐藏单元和过去时刻的输出$(y_1,y_2,...,y_{t-1})$，$y_0$为起始符号"s"或者$y_0=0$（很少见），解码出当前时刻的输出$y_t$，Decoder全部的输出表示为$(y_1,y_2,...,y_m)$
  • 由于当前时刻的输出只依赖输入和过去时刻的输出（不包含未来信息），因此这种输出的生成方式是自回归式的，也叫因果推断（Causal Inference）
• 训练时
  • Encoder行为不变，Decoder根据隐藏单元和过去时刻的label$({\hat{y}}_1,{\hat{y}}_2,...,{\hat{y}}_{t-1})$，解码出当前时刻的输出$y_t$，由于需要对每个$y_t$计算损失，而系统必须是因果的，因此每次解码时，需要Mask掉未来的信息，也就是全部置为$-\infty$（从而Softmax运算后接近0），当label为“s I am a student”，则Decoder每一时刻的输入，如下图
    
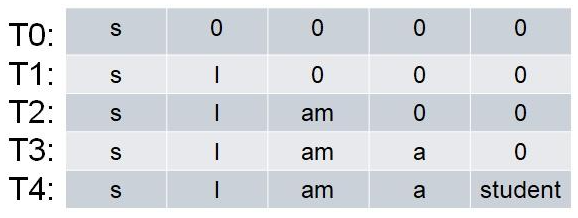
  • 这种将label作为Decoder的输入的训练方式叫做Teacher Forcing，类似上述推理时将输出作为Decoder的输入的训练方式叫做Free Running。Teacher Forcing允许并行计算出每个时刻的输出，因此是最常用的

Transformer的Encoder和Decoder

• Transformer的Encoder行为与上述一致，设Encoder的输入特征图形状为$(n,d_{model})$，即长度为n的序列，序列的每个元素是$d_{model}$维的向量，Encoder Layer（如下图左边重复N次的结构）是不改变输入特征图形状的，并且Encoder Layer内部的Sub-layer也是不改变输入特征图形状的，从而Encoder的输出特征图形状也为$(n,d_{model})$
• 这样设计的原因是：每个Encoder Layer都有两次残差连接（如下图中的Add运算），残差连接要求输入输出特征图形状不变，为了减少超参数，所以这样设计
  

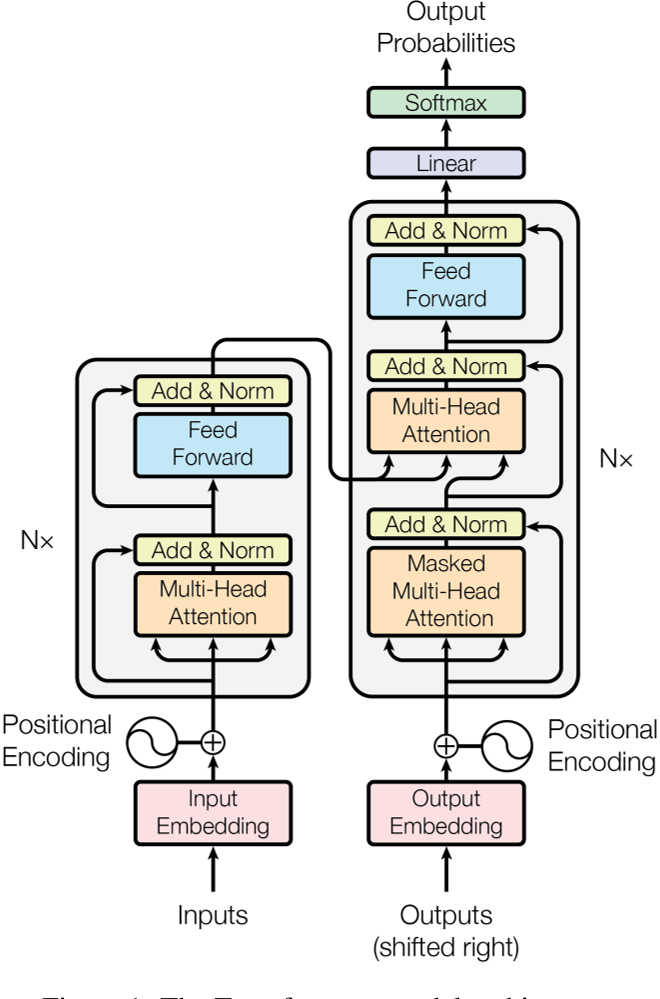
LayerNorm

• LayerNorm（如上图中的Norm运算）常用在可变长度序列任务里，接下来通过对比BatchNorm和LayerNorm，认识LayerNorm
  
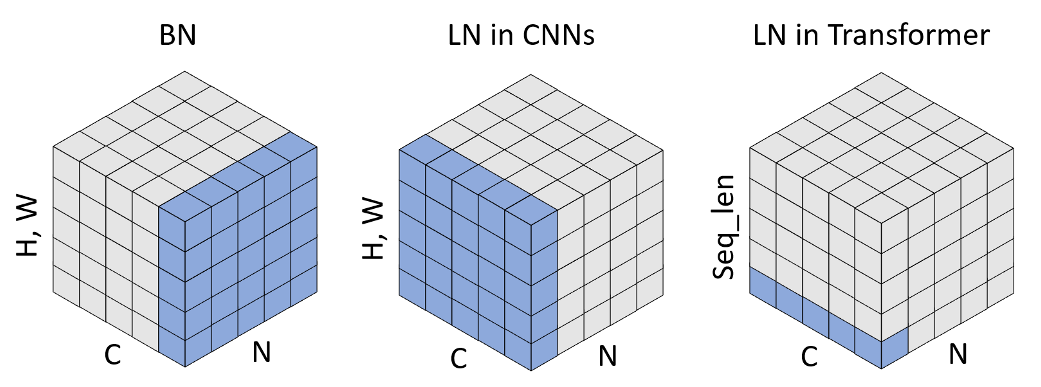
• 左图为BN，C为单个样本的特征维度（即特征图的Channels，表示特征的数量），H、W为特征的形状，因为特征可以是矩阵也可以是向量，因此统称特征形状。BN希望将每个特征变成0均值1方差，再变换成新的均值和方差，因此需要在一个Batch中，找寻每个样本的该特征，然后计算该特征的统计量，由于每个特征的统计量需要单独维护，因此构造BN需要传入特征的数量，也就是C。同时，BN的可学习参数$weight+bias=2\ast C$
• 中图为LN，LN希望不依赖Batch，将单个样本的所有特征变成0均值1方差，再变换成新的均值和方差，因此需要指定样本形状，告诉LN如何计算统计量，由于样本中的每个值，都进行均值和方差的变换，因此构造LN需要传入样本的形状，也就是C、H、W。同时，LN的可学习参数$weight+bias=2\ast C\ast H\ast W$
• 示例：

>>> input=torch.rand([1, 3, 2, 2])
>>> input
tensor([[[[0.1181, 0.6704],
          [0.7010, 0.8031]],

         [[0.0630, 0.2088],
          [0.2150, 0.6469]],

         [[0.5746, 0.4949],
          [0.3656, 0.7391]]]])

>>> layer_norm=torch.nn.LayerNorm((3, 2, 2), eps=1e-05)
>>> output=layer_norm(input)
>>> output
tensor([[[[-1.3912,  0.8131],
          [ 0.9349,  1.3424]],

         [[-1.6113, -1.0293],
          [-1.0047,  0.7191]],

         [[ 0.4308,  0.1126],
          [-0.4035,  1.0872]]]], grad_fn=<NativeLayerNormBackward0>)
>>> output[0].mean()
tensor(-1.7385e-07, grad_fn=<MeanBackward0>)
>>> output[0].std()
tensor(1.0445, grad_fn=<StdBackward0>)
>>> layer_norm.weight.shape
torch.Size([3, 2, 2])
>>> layer_norm.bias.shape
torch.Size([3, 2, 2])

# 等价于
>>> mean=input.mean(dim=(-1, -2, -3), keepdim=True)
>>> var=input.var(dim=(-1, -2, -3), keepdim=True, unbiased=False)
>>> (input-mean)/torch.sqrt(var+1e-05)
tensor([[[[-1.3912,  0.8131],
          [ 0.9349,  1.3424]],

         [[-1.6113, -1.0293],
          [-1.0047,  0.7191]],

         [[ 0.4308,  0.1126],
          [-0.4035,  1.0872]]]])
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43

• 上述两种情况为计算机视觉中的BN和LN，可以看出，BN训练时需要更新统计量，从而推理时使用统计量进行Norm，而LN训练和推理时的行为是一致的
• 在序列任务中，特征形状为1，多出来一个序列长度Seq_len，其他不变，1维的BN（BatchNorm1d）在N*Seq_len个帧中，计算每个特征的统计量，从而序列任务中的帧形状是C，因此LN要传入的帧形状是C，并且Input的形状中，C这个维度要放在最后
• 1维的BN常用于声纹识别，但是Transformer风格的模型基本都采用LN，并且LN是适用于任何特征形状的，BN则根据特征形状不同，衍生出BatchNorm1d、BatchNorm2d等
• 示例

>>> input=torch.rand([1, 200, 80])
>>> layer_norm=torch.nn.LayerNorm(80)
>>> layer_norm(input)[0][0].mean()
tensor(8.3447e-08, grad_fn=<MeanBackward0>)
>>> layer_norm(input)[0][1].mean()
tensor(-8.0466e-08, grad_fn=<MeanBackward0>)

>>> layer_norm(input)[0][0].std()
tensor(1.0063, grad_fn=<StdBackward0>)
>>> layer_norm(input)[0][1].std()
tensor(1.0063, grad_fn=<StdBackward0>)
1
2
3
4
5
6
7
8
9
10
11

• 在序列任务中采用LN而不是BN的原因
  • 序列任务的样本很多时候是不等长的，很多时候要补0帧，当batch-size较小时，BN的统计量波动较大，而LN是对每一帧进行Norm的，不受补0帧的影响
  • 训练时要构造一个Batch，因此序列长度只能固定，但是推理时序列长度是可变的，采用BN容易过拟合序列长度，LN则不容易过拟合序列长度

SA（自注意力）与CA（交叉注意力）

• 对于一个输入序列$(\text{seq-len},d_{model})$，SA通过Q、K、V计算矩阵，计算得到对应长度的Q、K、V序列，这些序列构成Q、K、V矩阵
• 如果Q、K、V矩阵完全由同一个序列计算而来，则称为自注意力SA；如果V、K矩阵由同一个序列计算而来，Q矩阵由另一个序列计算而来，则称为交叉注意力CA
• 需要注意，Decoder Layer中的第二个MHSA（如下图），从左到右的输入，计算顺序是V、K、Q，其中V、K是根据输入的隐藏单元进行计算的，即$(z_1,z_2,...,z_n)$，得到的V、K矩阵形状分别为$(n,d_k)$、$(n,d_v)$，而Q是根据输出的隐藏单元进行计算的，即$({\hat{z}}_1,{\hat{z}}_2,...,{\hat{z}}_m)$，得到的Q矩阵形状为$(m,d_k)$，因此这是一种CA运算
  
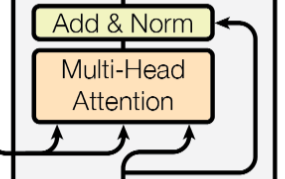
• SA和CA的后续运算是一致的，V、K、Q矩阵通过Attention函数计算Attention分数，然后对V矩阵进行加权求和，得到Attention的输出。Transformer用的Attention函数是Scaled Dot-Product Attention，公式如下：
  $$\text{Attention}(Q,K,V)=\text{softmax}(\frac{Q{K}^T}{\sqrt{d_k}})V$$
• 如果是Decoder的Attention函数则需要Mask掉softmax的输出，使得未来时刻对应的V接近0，如下图：
  
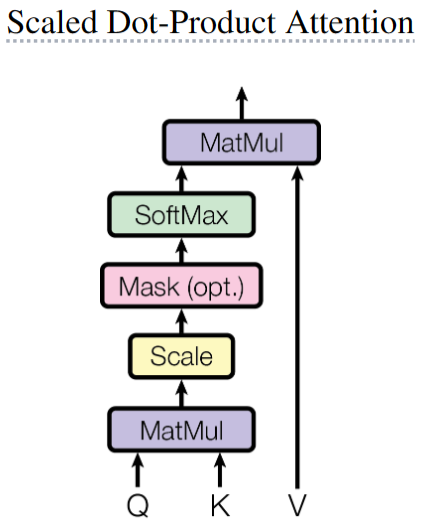
• 计算的细化过程如下图：
  
• $Q{K}^T$内积的含义是计算相似度，因此中间$(m,n)$矩阵的第m行，表示第m个query对所有key的相似度
• 之后除以$\sqrt{d_k}$进行Scale，并且Mask（具体操作为将未来时刻对应的点积结果置为$-\infty$，从而Softmax运算后接近0），然后对$(m,n)$矩阵的每一行进行Softmax
• 最后output矩阵的第m行，表示第m个权重对不同帧的value进行加权求和
• 需要注意的是
  • Attention最后的输出，序列长度由Q决定，向量维度由V决定
  • Q和K的向量维度一致，序列长度可以不同；K和V的序列长度一致，向量维度可以不同
  • Softmax是在计算第m个query对不同key的相似度的权重，求和为1
  • 除以$\sqrt{d_k}$的原因是因为后面需要进行Softmax运算，具有最大值主导效果。当$d_k$较小时，点积的结果差异不大，当$d_k$较大时，点积的结果波动较大（假设每个query和key都是0均值1方差的多维随机变量，则它们的点积$q\cdot k={\sum }_{i=1}^{d_k}{q}_i{k}_i$，为0均值$d_k$方差的多维随机变量），从而Softmax后，大量值接近0，这样会导致梯度变得很小，不利于收敛。因此除以一个值，会使得这些点积结果的值变小，从而Softmax运算的最大值主导效果不明显

MHSA

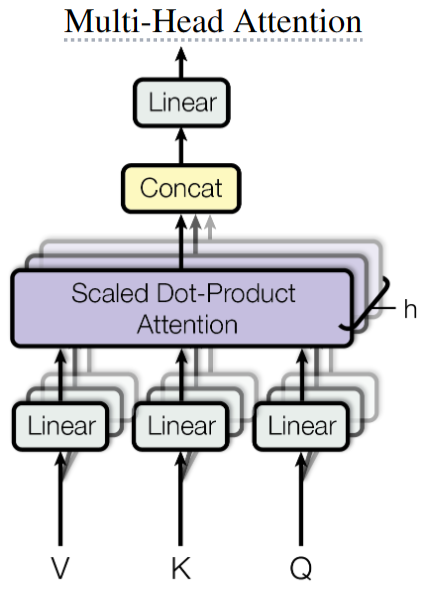
• 多头注意力的动机是：与其将输入投影到较高的维度，计算单个注意力，不如将输入投影到h个较低的维度，计算h个注意力，然后将h个注意力的输出在特征维度Concat起来，最后利用MLP进行多头特征聚合，得到MHSA的输出。MHSA的公式如下：
  $$\begin{array}{rl}\text{MultiHead}(Q,K,V)& =\text{Concat}(hea{d}_1,hea{d}_2,...,hea{d}_h)W^O\\ hea{d}_i& =\text{Attention}(Q_i,K_i,V_i)\end{array}$$
• 由于MHSA不能改变输入输出形状，所以每个SA的设计是：当$d_{model}=512$，$h=8$时，$d_k=d_v=d_{model}/h=64$
• 在实际运算时，可以通过一个大的矩阵运算，将输入投影到$(n,d_{model})$，然后在特征维度Split成h个矩阵，Q、K、V都可如此操作
• 因此一个MHSA的参数量：$4\ast d_{model}\ast d_{model}=4\ast d_{model}^2$，即Q、K、V加最后的MLP

FFN

• FFN的操作和MHSA中最后的MLP非常相似的，公式和图如下：
  $$\text{FFN}(x)=max(0,x{W}_1+b_1)W_2+b_2$$
  
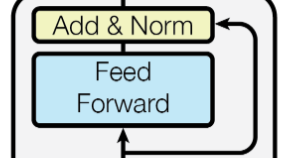
• 采用同一个MLP，对输入特征的每一帧进行维度变换（通常是增大为4倍），然后RELU，最后再采用另一个MLP，将输入特征的每一帧恢复回原来的维度
• 因此一个FFN的参数量：$d_{model}\ast 4\ast d_{model}+4\ast d_{model}\ast d_{model}=8\ast d_{model}^2$，即维度提升MLP加维度恢复MLP
• 综合，一个Encoder Layer的参数量为：$12\ast d_{model}^2$，一个Decoder Layer的参数量为：$16\ast d_{model}^2$
• 上述所有参数估计忽略LayerNorm的参数，因为其数量级较小

Embedding Layer和Softmax

• Encoder和Decoder的Embedding Layer，以及最后的Softmax输出前，都有一个MLP，在Transformer中，这三个MLP是共享参数的，形状都是$(\text{dict-len},d_{model})$，$\text{dict-len}$是字典大小
• 在Embedding Layer中，权重都被除以了$\sqrt{d_{model}}$，从而Embedding的输出范围在[-1, 1]附近，这是为了让Embedding的值范围靠近Positional Encoding，从而可以直接相加

Positional Encoding（位置编码）

• Attention的输出是不具有时序信息的，如果把输入打乱，那么也只会导致对应的输出打乱而已，不会有导致值变化，但序列任务往往关注时序信息，一件事先发生和后发生，意义是不一样的，因此需要对Attention的输入添加位置编码
• 位置编码的公式如下：
  $$\begin{array}{r}\text{PE}(pos,2i)=sin(pos/10000^{\frac{2i}{d_{model}}})\\ \text{PE}(pos,2i+1)=cos(pos/10000^{\frac{2i}{d_{model}}})\end{array}$$
• pos表示帧的位置，第二个参数表示特征的位置，奇偶交替，也就说：不同位置的同一特征，根据位置映射不同频率的正弦函数进行编码；同一位置的不同特征，根据奇偶分布映射不同频率的正弦函数进行编码
• 位置编码值的范围是[-1, 1]（Embedding的权重需要除以$\sqrt{d_{model}}$的原因），与Embedding对应元素相加，即可输入到Attention中