8方向连通域统计——two-pass算法（用于图像斑块数统计）_two pass算法

问题描述

现有一幅单通道灰度图像，图中像素共有0，1两种取值（取值代表类别代号，与算法无关）。现欲统计：每种取值的像素在图中构成的“斑块”的数目。斑块类似连通域的概念，这里我们定义像素数大于4的连通域才被算作一个斑块。

这个问题可以借助连通域标记算法解决。

连通域标记问题

连通域标记（Connected Component Labelling）问题， 主要有Two-Pass和Seed-Filling两种算法。本文介绍Two-Pass算法。

逐像素遍历图像，根据周围邻居像素的标签来给当前像素打标签。然后进行二次遍历，将同在一个斑块内的几种标签标记为一样（一个斑块内的几种标签，即等效标签，存储在并查集中）。

Two-Pass算法

只需要遍历两遍就可以完成标记。

First Pass

遍历每一个像素，如果像素p的值不为0，则考察它左上方的4个邻居的值。

• 如果邻居的值均为0，则给他打上标签（自增的，label_counter）。
• 如果邻居中存在不为0的值，取其中的最小值赋给p。随后利用并查集，把邻居的各种取值都建立联系（认定为同一个连通域）。

比如在下图中，像素p（红色块）的值不为0，考察其邻居的值，把2赋给p，同时把2和3标记为等价（在Union-Find set中，2和3有公共的根节点）。

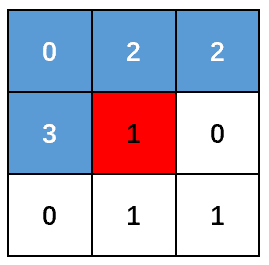
Second Pass

遍历每一个非0的像素，利用建好的并查集的find方法，把每一个像素的取值设为对应根节点的值。

Python实现

import numpy as np


class UnionFind:
    def __init__(self, n):
        """长度为n的并查集"""
        self.uf = [-1] * (n + 1)  # 列表0位置空出
        self.sets_count = n  # 判断并查集里共有几个集合, 初始化默认互相独立

    def find(self, p):
        """查找p的根结点(祖先)"""
        r = p  # 初始p
        while self.uf[p] > 0:
            p = self.uf[p]
        while r != p:  # 路径压缩, 把搜索下来的结点祖先全指向根结点
            self.uf[r], r = p, self.uf[r]
        return p

    def union(self, p, q):
        """连通p,q 让q指向p"""
        proot = self.find(p)
        qroot = self.find(q)
        if proot == qroot:
            return
        elif self.uf[proot] > self.uf[qroot]:  # 负数比较, 左边规模更小
            self.uf[qroot] += self.uf[proot]
            self.uf[proot] = qroot
        else:
            self.uf[proot] += self.uf[qroot]
            self.uf[qroot] = proot
        self.sets_count -= 1                   # 连通后集合总数减一

    def is_connected(self, p, q):
        """判断pq是否已经连通"""
        return self.find(p) == self.find(q)  # 即判断两个结点是否是属于同一个祖先


def im_binary(data: np.ndarray, target_value: int):
    return np.where(data == target_value, 1, 0)


def im_padding(data: np.ndarray):
    return np.pad(data, ((1, 1), (1, 1)), 'constant')


def first_pass(data, uf_set):
    offsets = [[-1, -1], [0, -1], [-1, 1], [-1,  0]]
    label_counter = 2
    for y in range(1, data.shape[0]-1):
        for x in range(1, data.shape[1]-1):
            if data[y, x] == 0:
                continue
            neighbor = []
            for offset in offsets:
                if data[y + offset[0], x + offset[1]] != 0:
                    neighbor.append(data[y + offset[0], x + offset[1]])
            neighbor = np.unique(neighbor)
            if len(neighbor) == 0:
                data[y, x] = label_counter
                label_counter += 1
            elif len(neighbor) == 1:
                data[y, x] = neighbor[0]
            else:
                # 邻居内有多重label, 这种情况要把最小值赋给data[y, x], 同时建立值之间的联系.
                data[y, x] = neighbor[0]
                for n in neighbor:
                    uf_set.union(int(neighbor[0]), int(n))


def second_pass(data, uf_set):
    for y in range(data.shape[0]):
        for x in range(data.shape[1]):
            if data[y, x] != 0:
                data[y, x] = uf_set.find(int(data[y, x]))
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74

• im_binary() 方法把一个图像中等于target_value的值置为1，其余的置为0，实现二值化。
• im_padding() 把图片周围补一圈0，这样才能用下面的算法。

例子

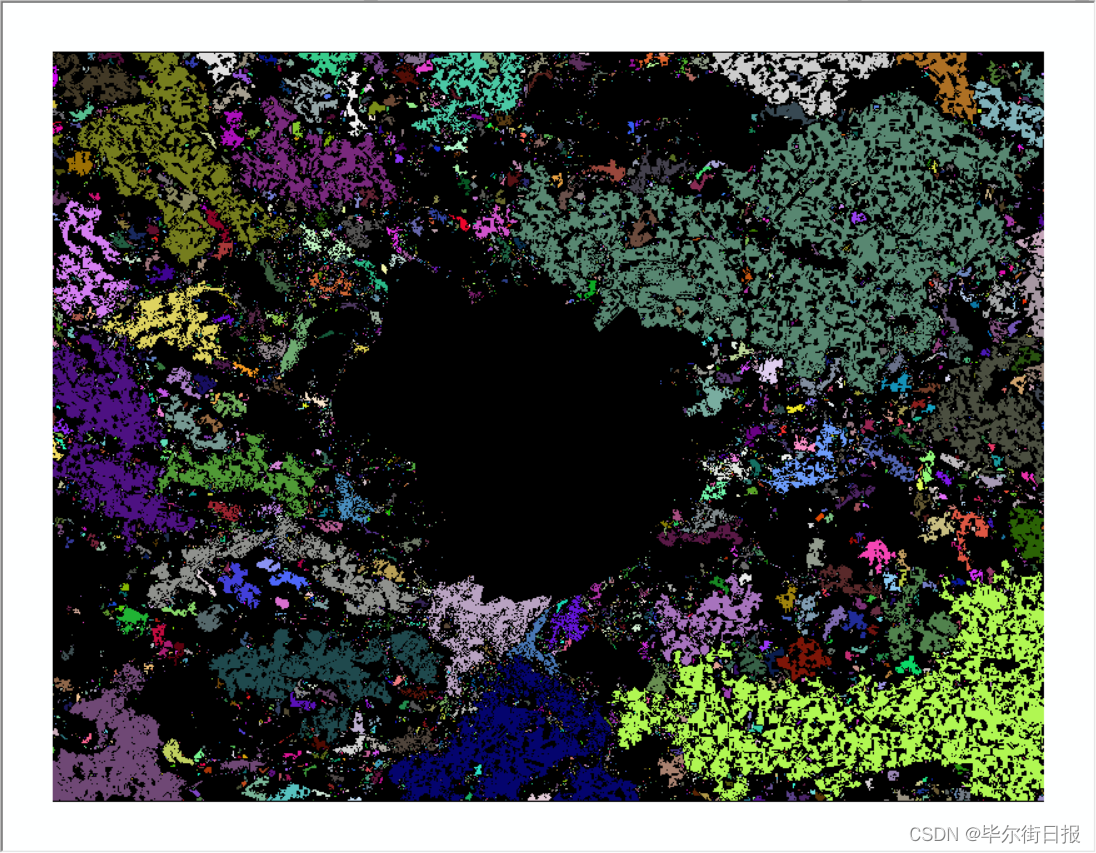
输入是一个植被指数（NDVI）单通道图像。希望把NDVI值大于0.1的部分设为1，小于的部分设为0，再计算1构成的连通域（图斑）的数量，并实现可视化。

def count_patch(data, get_img=False):
    # 统计某一种类别的图斑数. 返回各个图斑的像素数，和结果图.
    ufSet = UnionFind(1000000)
    first_pass(data, ufSet)
    second_pass(data, ufSet)

    count_dic = {}
    for y in range(1, data.shape[0] - 1):
        for x in range(1, data.shape[1] - 1):
            if data[y, x] in count_dic:
                count_dic[data[y, x]] += 1
            else:
                count_dic[data[y, x]] = 1

    count_dic.pop(0)

    if get_img:
        return list(count_dic.values()), data
    else:
        return list(count_dic.values())
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20

结果图如下（同一连通域被标记成一种颜色）：