企业生产过程能力分析(CPK)_cpk数据分析怎么做

系列文章目录

---

前言

计算Cp和Cpk前提：数据正态、过程稳定、数据独立、MSA合格。

一、Cpk的定义

Cpk是指工序在一定时间里，处于控制状态(稳定状态)下的实际加工能力；Cpk也叫制程能力指数/工序能力指数/过程能力指数；

二、Cp、Cpk、Pp、Ppk之间的关系

1. USL(Upper Specification Limit)：规格上限

2. LSL(Low Specification Limit)：规格下限

3. T(规格公差)：T=USL-LSL

4. C(标准值)：图纸定义的标准值

5. X平均值=（X1+X2+X3+·····+Xn）/n

6. Sigma(标准差)：Excel中的STDEV函数自动计算一组数据的标准差；
   

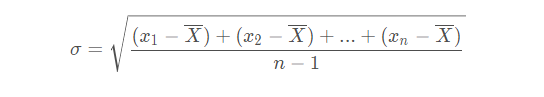
7. Cp(制程精密度)：衡量规格公差宽度/制程变异宽度
   双边规格：Cp=(USL-LSL)/6Sigma
   单边规格：
   Cpu=(USL-X平均值)/3Sigma
   Cpl =(X平均值-LSL)/3Sigma

8. Ca(制程准确度)：衡量实际平均值与规格中心值的一致性；
   双边规格：Ca=(X平均值-C)/(T/2)
   单边规格：不存在规格中心，因此不存在Ca；

9. Ca等级评定
   

10. Cpk的计算公式Cpk=Cp(1-|Ca|)

11. Cpk等级评定
    

1.能力指数Cp

Cp能力指数使用上下规格之间的差异来定义可用范围，并将其与以最小方差运行的过程所需的通用范围进行比较。所需的通用范围为6倍的组内标准差，即6Sigma(x)

能力指数Cp=(USL-LSL)/6Sigma(x)=可用范围/过程所需范围

因此，Cp是指数据的规格范围是波动的多少倍，值越高，说明数据波动幅度相对较小，过程能力强；然而，Cp没有考虑数据的居中性，有可能数据波动范围很小，却是在规格范围外波动；

2.中心能力指数Cpk

Cpk则在Cp的基础上考虑了数据波动的中心位置，从而可以用来衡量过程的中心能力

中心能力指数Cpk = Min{(USL- X平均值),(X平均值-LSL)}/3Sigma(X)=有效可用范围/过程所需范围

说明：下图说明Cp与Cpk的差异，当数据波动一致，数据中心偏移时，Cp不变，但Cpk变小了；

3.性能指数Pp

Pp性能指数使用上下规格之间的差异作为可用范围，并将其与过去过程实际表现的标准差做比较，在计算能力指数时，我们用的是组内标准差Sigma(X),而在计算性能指数时用的是样本标准差s;

性能指数Pp = (USL-LSL)/6s =可用范围/过程过去的波动范围

因此，性能指数Pp将可用于评价过去的过程表现，但是，它不考虑过程表现的中心位置;

4.中心性能指数Ppk

中心性能指数则通过定义过程的有效可用范围考虑了中心位置

中心性能指数Ppk = Min{(USL-X平均值),(X平均值-LSL)}/3s=有效可用范围/过程过去的波动范围

5.关联性

图上半部分的Cp与Cpk描述的是过程的潜在能力，下半部分Pp与Ppk描述的是过程过去所表现出来的性能；随着一个过程的运行越来越接近发挥其全部的潜力，Pp和Ppk将向上移动，接近上层的Cp和Cpk;

• 左侧两个指数假定了过程中心与规范中心重叠，而右侧考虑了二者之间的偏离程度。当过程中心接近规格的中心时，右边的值会向左边靠近；
• 当一个过程稳定的运行，顶层和底层的指数将具有相似的值，但左右两侧的值之间会存在一些差异，这种差异是过程中心偏移带来的影响；
• 当一个过程即稳定又无偏移地运行时，这四个指数将非常接近；
• Cp是最佳状态下的潜在过程能力值，而性能指数Ppk描述的是过去的过程性能，这二者的差距就是我们过程改善的机会；

示例分析：

1. 过程一：
   Cp=1.48、Cpk=0.95
   Pp=1.43、Ppk=0.92
   过程一的Cp与Pp,Cpk与Ppk均较接近，说明过程较为稳定；Cpk与Ppk又明显小于Cp与Pp，说明过程中心偏移，此时我们要做的是调整过程的中心位置；

2. 过程二：
   Cp=5.38、Cpk=2.00
   Pp=2.40、Ppk=0.90
   虽然这四个值中有三个数值是比较大，但是过程能力指数和性能指数之间的差异告诉我们，这个过程正在不稳定运行，Cpk与Cp以及Ppk与Pp的差异告诉我们这个过程没有在接近规格中心的地方运行，偏移了中心；Ppk和Cp之间的巨大差异表明工艺改进的机会很大；针对此类情况我们首先要稳定过程，消除组间的变差，然后将过程向中心修正；

三、Cpk、Ppk的区别

从定义上来说，Ppk反映的是过程的实际表现，Cpk反映的是过程的能力。比如：小明同学聪明、刻苦、学习认真，如果正常发挥可以考到班级前三，但有一次因为有些心事，心情不好没有考好，只考了班级第十；此时，考前三是小明的能力，即小明Cpk;而考了班级第十是小明的实际表现，即小明Ppk;所以，Cpk是制造过程能拿出的最佳表现，所以Cpk一定是大于等于Ppk的。

四、案例介绍

1.EXCEL批量计算Ppk

2.minitab计算并生成Cpk图

1. 收集数据&复制数据到minitab工作表；
   

2. 正态性检验

从上图可以看出，正态性检验P值大于0.05，即NUM3数据满足正态分布；
3. Cpk图
六合一：

单个图步骤一：


单个图步骤二：

---

总结

分享：
研究真理可以有三个目的：当我们探索时，就要发现到真理；当我们找到时，就要证明真理；当我们审查时，就要把它同谬误区别开来。