devbox
不正经
这个屌丝很懒，什么也没留下！
关注作者
热门标签
热门文章
当前位置:   article > 正文

【深度视觉】第九章：复现SOTA 模型：GoogLeNet

作者：不正经 | 2024-04-24 15:06:00

赞

踩

【深度视觉】第九章：复现SOTA 模型：GoogLeNet

十一、复现SOTA 模型：GoogLeNet

在深度学习领域，最前沿、最先进的架构被称为state-of-the-art models,SOTA model, 就是达到了SOTA level的水平。我们前面的模型只有VGG架构是达到了准SOTA Level的架构，因为它将加深深度的思路的简洁性发挥到了极致。但是VGG的致命缺点是参数量巨大，导致计算量过大，proper training变得非常困难。

1、GoogLeNet诞生的思路及框架解读
诞生于2015年的inceptionV1是googlenet的核心架构，是谷歌团队和其他高校联合研发的。发表的论文是《going deeper with convolutions》加深卷积网络。
谷歌引入了一种全新的网络架构：inception block, inception直译是'起始时间'，也果然是inception块的出现，成为了深度视觉发展史上的一个新起点。它采用了一种与传统CNN完全不同的构建思路。因为之前的架构从LeNet到VGG都是在串联卷积层、池化层和线性层，在这种串联方式下，参数量就是绕不开的死结，而googlenet的inception块中的并联架构，完美得避开了天量参数问题。

当GoogLeNet的架构摆到你面前时，你会发现它除了并联思路和辅助分类器外，其他各方面也并无特别之处。所以也别去纠结它背后的理论了。下面是inceptionV1的架构：

看到inceptionV1架构后，第一个想法就是谷歌团队是如何想到这样搭建inception块的？如何想到并联的？为什么是这样的并联？为啥不是其他的并联？其实这个inception块的具体架构不是人脑想出来的，是google团队开发一个网络架构构造算法，让这个算法向着使用稠密成分逼近稀疏架构的方向进行训练，让这个算法产生数个可能有效的密集架构，再选出一个学习能力最强的密集架构及其相关参数，上面的inception块就是算法选出的其中的一个最强的块儿，再把数个inception块串联起来就是googlenet。

由于这个构架是由算法构建的，所以我们也不能从"改变卷积核尺寸"、"改变步长和padding"等层面进行调参了，因此也不需要调超参数了。

  • googlenet的创新点和借鉴前人之处：

最大的创新就是：
（1）并联架构的inception块儿，这是前无古人后无来者的惊人之处。另外，在后来的InceptionV3中，在不改变感受野同时减少参数的情况下，采用1*n和n*1的卷积核并联来代替InceptionV1-V2中n*n的卷积核（发掘特征图的高的特征，以及特征图的宽的特征）。但这种方法在大维度的特征图上表现不好，在特征图12-20维度上表现较好。
（2）添加了两个辅助分类器帮助训练。当时的解释是：避免梯度消失，用于向前传导梯度，也有一定的正则化效果，防止过拟合。但是这两个辅助分类器后面被证实没什么用，V2V3都不用了。但借鉴意义仍存。

借鉴前人之处是：
（1）大量使用1x1的卷积核进行降通道处理，减少参数量。这是受NIN的启发，NIN是第一个使用1x1的卷积核的网络。
（2）丢弃全连接层，使用GAP平均池化层(大大的减少了模型的参数)。NIN也是第一个没有使用线性层的网络。另外鉴于VGG的线性层的巨量参数，googlenet放弃了全连接层。但是实际上googlenet在最后还是加了一个全连接层，但主要目的是为了方便以后如果分类的类别数目变了，大家可以通过微调finetune就可以迁移学习了，这个线性层并不承担传统意义上的全连接层的信息混合和特征间函数关系的学习，仅仅是充当的是一个分类的作用而已。也所以我们为什么说googlenet舍弃了全连接层。
（3）激活函数都使用的是RELU激活函数。这个就不用多说了，从Alexnet以后大家基本都用relu。

  • Inception技术演进：

V1（GoogLeNet）-> BN-Inception –> V2 –> V3 –> V4 –> Inception-ResNet –> Xception
随着架构的迭代更新，InceptionV3和V4已经是经典的SOTA模型了，可以在ImageNet数据集上达到3%的错误率。
Inception系列的参数少，精度高，计算效率高，使得在边缘设备上也可以使用。以下是2017年做的统计，左边的是各个网络的top1准确率，右边的是计算量及准确率的模型，可以看到inception系列真的是计算量少准确率又高。

3、inception块详细解读
VGG和alexnet都是从上往下串联卷积层，inception块却使用了多路卷积，然后堆叠，用密集模块去近似出局部最优稀疏结构。
下图是我到网上截的图，上面部分是原生inception块(naive version),下面部分是改进版inception块，我们现在讲的inceptionV1就是改进版的架构。

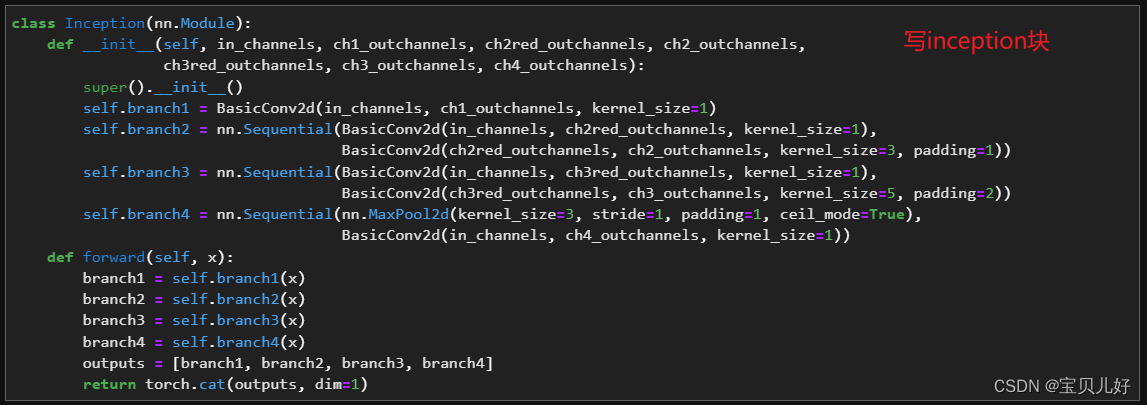
从上图可以看出一个inception块中有4条分支branch, 每个分支中包含的组件(卷积层和池化)都是不一样的。下面拿inception 3a为例：

第一个分支是1x1卷积。按照论文的说法就是，这支branch就是用来提取特征的，因为是逐点卷积，没有信息损失也没有相对位置信息损失。
第二个分支是先1x1卷积再串联一个3x3卷积。论文说这支branch中的1x1卷积是用来降低通道数。就是降低参数量的作用。3x3卷积是用来提取相对位置信息的。
第三个分支是先1x1卷积再串联一个5x5卷积。论文说这支branch中的1x1卷积也是用来降低通道数。5x5卷积是用来提取更大范围内的信息的。
第四个分支是先最大池化再串联一个1x1卷积。其中最大池化步长是1，而且输出尺度不变(padding_mode=same),所以它就是来提取最有用的信息的(值最大说明携带的信息量越大)。后面又串联的1x1卷积也是用来降低通道，将参数量的。

小结：
inception块中1x1卷积层的作用：有的是用来提取特征的(branch1)，有的却是用来降参的(branch2,branch3,branch4)。
整个googlenet架构中的最大池化层：不在inception块中的最大池化层是用来消减特征图尺寸的。在inception块中的最大池化层却是用来提取信息的！

由于上面的架构是网络架构构造算法构造出来的。所以：

（1）我们再也不用需要考虑使用什么尺寸的卷积核了，一个inception块就包含了各种尺寸的卷积核：
1*1小卷积核扫描可以最大程度的保留像素和像素之间的位置信息。
3*3和5*5大卷积核则更擅长提取相邻像素之间的联系，就是更能捕捉相邻像素之间的信息。
最大池化层又是用来提取局部中的最大信息的。
上面的小卷积核、大卷积核、池化层又都是并联的，并联就意味着原图中的信息可以分别以大核、小核、重叠池化等方式都提取一遍信息，这样原图中信息就会被充分提取了。以前的串联结构只能提取一次，然后在此基础上再提取一次。并联就可以同时提取，这样提取的特征就更可能会是更全面的特征了。用官方一点的话说就是：利用不同大小的卷积核实现不同尺度的感知，最后进行融合，可以得到图像更好的表征（即探索特征图上不同邻域内的“相关性”）。

（2）这个块里面的线路是并联的方式，并联就可以并行计算了，计算效率就大大提升了。并联就可以同时进行扫描计算，线路和线路之间的扫描计算互不干扰，所以在扫描计算时就可以多线程计算。

（3）每条线路上的特征图与特征图之间就是稠密链接，没有人为出现空隙。所以这个inception块的结构是稠密的，就可以利用GPU等硬件擅长处理相似结构的稠密数据的特点，提高计算效率。

（4）这里的1*1卷积核在这个块中是一个奇妙的存在，它一定程度上可以看作是降维、聚类、提升非线性表达能力的三大功能。
首先，1*1卷积核是把输入的数据(192*28*28)中28*28格子中的每个数字都是看到了的，所以它一个像素的信息都没有损失，但是它强行将192个通道压缩到96个通道，所以它实现了降维的操作，而降维就意味着降低参数量和加深网络深度(这之前我们讲1*1卷积核的作用时是有总结出来的)。 其次，有论文说：如果说在DNN中线性层上的神经元表示一个个特征，这些特征有的是可以聚类的，同理CNN中的特征图也就可以被看做是携带相似信息的密集神经元，当1*1卷积核把192个通道压缩到96个通道，整体上看就是把信息压缩了，所以好像是聚类了，其实是聚合信息了。再次，我们通常都会在卷积层后面跟一个激活层，1*1卷积层也不例外，而激活层是非线性变换的，所以它提升了非线性表达能力。

4、辅助分类器
除了上述主体架构以外，googlenet还使用了辅助分类器auxiliary classifier，用来提升模型性能，目前这种辅助分类器已经成为一个常规的操作，经常出现在架构里面。
googlenet V1的辅助分类器是串联在inception(4a)和inception(4d)后面的，所以有两个辅助分类器。下图是inception(4a)后面串联的辅助分类器的架构：

辅助分类器通俗的讲就是在主分类器数据流动的过程中添加额外的一个softmax分类器，这个辅助的分类器也可以当作一个块, 由特征图的数据输入这个块。 整个googlenet跑完会有三个softmax结果的，这三个结果的区别只是每个结果的网络深度不一样而已。

  • 那为什么要得出三个结果呢？

因为数据传递到inception4a时效果就已经非常不错了，传递到inception4d后效果就更不错了，所以我们就可以认为这几个节点输出的特征就已经是非常重要的特征了，所以我们是不是可以加重这些特征的使用，就是加重这些特征的使用权重，那么整个模型就应该可以有更好的效果，所以在这两个地方我们分别串联一个辅助分类器，让这些最有用的特征中途导出，所以最终就输出了三个softmax结果。

得到三个softmax结果后，根据结果构造损失函数，再对三个损失函数进行加权平均，求一个最终的平均损失函数，再基于这个最终的损失进行反向传播求这个最终损失函数的梯度进行迭代优化。这就是对中间的特征进行加重。这种方法有一点模型融合和模型集成的思想。因为加权平均就相当于投票，googlenet给中间的辅助分类器的权重是0.3，这有点像集成的思想，集成是可以提升模型效果的。所以一次训练生成三个网络，就是集成。现在好的算法都是集成算法。

除了模型融合和模型集成说外，还有人认为主要原因是为了防止避免梯度消失。因为反向传播时如果有一层求导为0，链式求导结果则为0，很容易梯度消失。

还有人认为主要作用是正则化作用（防止过拟合）。在后续的研究中，Google团队研究人员发现辅助分类器在训练早期并没有改善收敛：在两个模型达到高精度之前，两种网络的训练进度看起来几乎相同；接近训练结束，有辅助分支的网络才开始超越没有任何分支的网络的准确性，达到了更高的稳定水平，因此辅助分类器更多的还是起到了一个正则化的作用，就是防止过拟合的作用。

不管这两个辅助分类器到底有啥作用，但在后面的实证中被证实其实没啥用，所以后面的V2V3都不用了。

5、局部响应归一化local response normalization, LRN
LRN功能最初是在AlexNet的架构中被使用的，VGG中也有它的身影。但这两个模型都实证了，这个功能对模型效果提升没有太多作用，现在基本被BN替代，使用BN的inception被称为inceptionV2,所以我们现在都是在每个卷积层的后面加上BN层以确保更好的拟合效果。

6、数据增强
其实在ILSVRC-2014比赛中，google团队最后是训练了7个模型，并且把每张图片通过各种图片增强的技巧增加到144张，然后让每个模型都检测这144张图片后，得出的结果再集成，最后获得了ILSVRC-2014冠军。所以数据增强操作也是必不可少的一环。

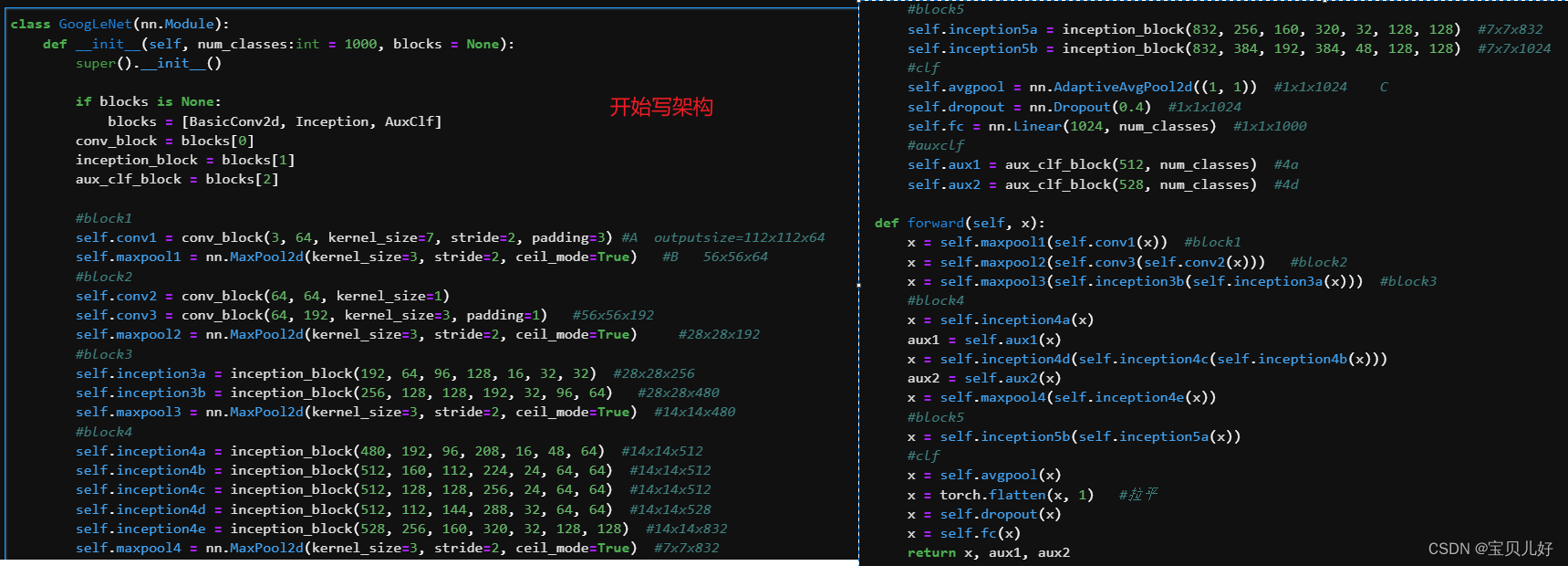
7、GoogLeNet的整体架构
（1）googlenet是数个inception块与传统卷积结构的串联，其中inception块内部是稠密部件的并联。
（2）googlenet是基于image数据集的，这个数据集的数据结构就是3x224x224。
（3）在inception块里面的pool是用来提取特征的，在好几个inception块串联后面又串联的pool是用来将特征图尺寸减半的。
（4）inception块出现在网络后面效果会更好一些，无理论支持是实验结果。
（5）googlenet网络里面是没有线性层的，网络最后的linear只是为了softmax1000个分类而存在的输出层而已，数据通过这个线性层没有像DNN中那样的有要学习的参数的那样的线性层。
（6）所有的卷积层都默认bias=False,并且都默认卷积层后面紧跟BN层，并且还默认BN层后紧跟ReLU操作。对于SOTA模型来说行业默认的就是卷积层后面紧跟bn层，除非特殊说明不需要跟BN层。

这里再给大家展示一下torchvision.models.GoogLeNet()的网络架构，和详细参数情况，方便后面代码复现这个架构：

我们看论文一般看到的架构参数都是上图的样子，很多同学不知道这些数都表示什么，下面我们一点点理一下上面的架构参数。
说明：所有卷积层都默认bias=False,并且都默认卷积层后面紧跟BN层，并且还默认BN层后紧跟ReLU操作。后面不再重复说明。
1：输入图像为224x224x3

2：本层卷积层是Conv2d(in_channels=3,out_channels=64,kernel_size=7,stride=2,padding=3)
输出特征图尺寸是(224-7+3x2)/2+1=112.5(向下取整)=112，输出数据结构是64x112x112。
本层卷积层的参数量是7*7*3*64=9408，本层BN层的参数量是2*64=128，本层参数总量是9408+128=9536。

3：本层MaxPool2d(kernel_size=3，stride=2，padding=0)
本层输出特征图尺寸是((112 -3)/2)+1=55.5(向上取整)=56，输出数据结构是64x56x56。本层无参数。

4-1：本层卷积层是Conv2d(in_channels=64,out_channels=64,kernel_size=1,stride=1,padding=0)
输出特征图特征图尺寸是64x56x56。本层的参数量是：64*64(卷积层的) + 2*64(BN层的)=4224。

4-2：本层卷积层是Conv2d(in_channels=64,out_channels=192,kernel_size=3,stride=1,padding=1)
本层输出特征图尺寸是(56-3+1x2)/1+1=56，输出数据结构192x56x56。本层的参数量是9*64*192 + 2*192=110976。

5：本层MaxPool2d(kernel_size=3，stride=2，padding=0)
本层输出特征图尺寸是((56 - 3)/2)+1=27.5(向上取整)=28，输出数据结构为192x28x28。本层无参数。

Inception 3a：
（1）Conv2d(in_channels=192,out_channels=64,kernel_size=1) ，输出64x28x28 ，参数量192*64+2*64=12416
（2）Conv2d(in_channels=192,out_channels=96,kernel_size=1)->Conv2d(in_channels=96,out_channels=128,kernel_size=3,stride=1,padding=1)
输出128x28x28 ，参数量192*96+2*96+9*96*128+2*128=129472
（3）Conv2d(in_channels=192,out_channels=16,kernel_size=1)->Conv2d(in_channels=16,out_channels=32,kernel_size=5,stride=1,padding=2)
输出32x28x28 ，参数量192*16+2*16+25*16*32+2*32=15968
（4）MaxPool2d(kernel_size=3，stride=1，padding_mode=same)->Conv2d(in_channels=192,out_channels=32,kernel_size=1) 输出32x28x28 ，参数量192*32+2*32=6208
总输出：(64+128+32+32=256*28*28) ,总参数量：12416+129472+15968+6208=164064

后面的模块同理，左侧的架构图和右侧的参数表相互对照着写。因为左侧架构图中有没有标出的层，比如AB两处没有标出最大池化层，C处没有标出dropout层！而右侧参数表又没有把1x1卷积层的参数单独写出来，看着非常迷惑，而且参数表里面也没有辅助分类器的参数情况。所以大家要先自己把每层都计算清楚，明白要使用什么参数才能输出表里的输出结果。

此外还要说明一点就是nn.Conv2d()的输出是默认的向下取整的，就是多余的像素直接抛弃了，而且这个默认做法是写死在底层代码中的，如果你不想抛弃边角像素，你就得用padding和padding_mode两个参数搭配处理了。但是nn.MaxPool2d和nn.AvgPool2d是有一个参数ceil_mode，默认ceil_mode=False就是向下取整，也就是默认也是抛弃边角像素，但是你可以通过调整参数ceil_mode=True来进行向上取整，就是自动给你加值为0的黑边，然后再取最大或者平均。这些细节你都非常清楚了，参数的填写就不成问题了。

8、代码复现GoogLeNet




下面是复现代码及测试结果：

  1. import torch
  2. import torch.nn as nn
  3. from torchinfo import summary
  4.  
  5. class Googlenet(nn.Module):
  6.     def __init__(self, num_classes:int = 1000):
  7.         super().__init__()
  8.         self.conv1 = nn.Sequential(nn.Conv2d(3,64,7,2,3,bias=False), nn.BatchNorm2d(64), nn.ReLU(inplace=True))#[1, 64, 112, 112]
  9.         self.pool1 = nn.MaxPool2d(kernel_size=3,stride=2,ceil_mode=True)  #[1, 64, 56, 56]
  10.         self.conv2 = nn.Sequential(nn.Conv2d(64,64,1,bias=False), nn.BatchNorm2d(64), nn.ReLU(inplace=True))  #[1, 64, 56, 56]
  11.         self.conv3 = nn.Sequential(nn.Conv2d(64,192,3,1,1,bias=False), nn.BatchNorm2d(192), nn.ReLU(inplace=True))#[1, 192, 56, 56]
  12.         self.pool2 = nn.MaxPool2d(kernel_size=3,stride=2,ceil_mode=True)  #[1, 192, 28, 28]
  13.         
  14.         #inception 3a 的输入：[1, 192, 28, 28]
  15.         self.inception3a1 = nn.Sequential(nn.Conv2d(192,64,1,bias=False), nn.BatchNorm2d(64), nn.ReLU(inplace=True)) #[1, 64, 28, 28]
  16.         self.inception3a2 = nn.Sequential(nn.Conv2d(192,96,1,bias=False), nn.BatchNorm2d(96), nn.ReLU(inplace=True),
  17.                                          nn.Conv2d(96,128,3,1,1,bias=False), nn.BatchNorm2d(128), nn.ReLU(inplace=True))#[1, 128, 28, 28]
  18.         self.inception3a3 = nn.Sequential(nn.Conv2d(192,16,1,bias=False), nn.BatchNorm2d(16), nn.ReLU(inplace=True),
  19.                                          nn.Conv2d(16,32,5,1,2,bias=False), nn.BatchNorm2d(32), nn.ReLU(inplace=True)) #[1, 32, 28, 28]
  20.         self.inception3a4 = nn.Sequential(nn.MaxPool2d(kernel_size=3,stride=1,padding=1,ceil_mode=True), 
  21.                                          nn.Conv2d(192,32,1,bias=False), nn.BatchNorm2d(32), nn.ReLU(inplace=True)) #[1, 32, 28, 28]
  22.         
  23.         #inception 3b的输入：[1, 256, 28, 28]
  24.         self.inception3b1 = nn.Sequential(nn.Conv2d(256,128,1,bias=False), nn.BatchNorm2d(128), nn.ReLU(inplace=True)) #[1, 128, 28, 28]
  25.         self.inception3b2 = nn.Sequential(nn.Conv2d(256,128,1,bias=False), nn.BatchNorm2d(128), nn.ReLU(inplace=True),
  26.                                          nn.Conv2d(128,192,3,1,1,bias=False), nn.BatchNorm2d(192), nn.ReLU(inplace=True))#[1, 192, 28, 28]
  27.         self.inception3b3 = nn.Sequential(nn.Conv2d(256,32,1,bias=False), nn.BatchNorm2d(32), nn.ReLU(inplace=True),
  28.                                          nn.Conv2d(32,96,5,1,2,bias=False), nn.BatchNorm2d(96), nn.ReLU(inplace=True)) #[1, 96, 28, 28]
  29.         self.inception3b4 = nn.Sequential(nn.MaxPool2d(kernel_size=3,stride=1,padding=1,ceil_mode=True), 
  30.                                          nn.Conv2d(256,64,1,bias=False), nn.BatchNorm2d(64), nn.ReLU(inplace=True)) #[1, 64, 28, 28]
  31.         
  32.         #maxpool的输入：[1, 480, 28, 28]   128+192+96+64=480   
  33.         self.pool3 = nn.MaxPool2d(kernel_size=3,stride=2,ceil_mode=True) #[1, 480, 14, 14]
  34.         
  35.         #inception 4a的输入：[1, 480, 14, 14]
  36.         self.inception4a1 = nn.Sequential(nn.Conv2d(480,192,1,bias=False), nn.BatchNorm2d(192), nn.ReLU(inplace=True)) #[1, 192, 14, 14]
  37.         self.inception4a2 = nn.Sequential(nn.Conv2d(480,96,1,bias=False), nn.BatchNorm2d(96), nn.ReLU(inplace=True),
  38.                                          nn.Conv2d(96,208,3,1,1,bias=False), nn.BatchNorm2d(208), nn.ReLU(inplace=True))#[1, 208, 14, 14]
  39.         self.inception4a3 = nn.Sequential(nn.Conv2d(480,16,1,bias=False), nn.BatchNorm2d(16), nn.ReLU(inplace=True),
  40.                                          nn.Conv2d(16,48,5,1,2,bias=False), nn.BatchNorm2d(48), nn.ReLU(inplace=True)) #[1, 48, 14, 14]
  41.         self.inception4a4 = nn.Sequential(nn.MaxPool2d(kernel_size=3,stride=1,padding=1,ceil_mode=True), 
  42.                                          nn.Conv2d(480,64,1,bias=False), nn.BatchNorm2d(64), nn.ReLU(inplace=True)) #[1, 64, 14, 14]
  43.         
  44.         #aux1的输入：：[1, 512, 14, 14]  192+208+48+64=512
  45.         self.aux1_f = nn.Sequential(nn.AvgPool2d(kernel_size=5, stride=3),   #[1, 512, 4, 4]
  46.                                  nn.Conv2d(512,128,1,bias=False), nn.BatchNorm2d(128), nn.ReLU(inplace=True)) #[1, 128, 4, 4]
  47.         self.aux1_c = nn.Sequential(nn.Linear(128*4*4, 1024), nn.ReLU(inplace=True), nn.Dropout(0.7), nn.Linear(1024, num_classes))
  48.  
  49.         #inception 4b的输入：[1, 512, 14, 14]  192+208+48+64=512
  50.         self.inception4b1 = nn.Sequential(nn.Conv2d(512,160,1,bias=False), nn.BatchNorm2d(160), nn.ReLU(inplace=True)) #[1, 160, 14, 14]
  51.         self.inception4b2 = nn.Sequential(nn.Conv2d(512,112,1,bias=False), nn.BatchNorm2d(112), nn.ReLU(inplace=True),
  52.                                          nn.Conv2d(112,224,3,1,1,bias=False), nn.BatchNorm2d(224), nn.ReLU(inplace=True))#[1, 224, 14, 14]
  53.         self.inception4b3 = nn.Sequential(nn.Conv2d(512,24,1,bias=False), nn.BatchNorm2d(24), nn.ReLU(inplace=True),
  54.                                          nn.Conv2d(24,64,5,1,2,bias=False), nn.BatchNorm2d(64), nn.ReLU(inplace=True)) #[1, 64, 14, 14]
  55.         self.inception4b4 = nn.Sequential(nn.MaxPool2d(kernel_size=3,stride=1,padding=1,ceil_mode=True), 
  56.                                          nn.Conv2d(512,64,1,bias=False), nn.BatchNorm2d(64), nn.ReLU(inplace=True)) #[1, 64, 14, 14]
  57.         
  58.         #inception 4c的输入：[1,512,14,14]      160+224+64+64=512
  59.         self.inception4c1 = nn.Sequential(nn.Conv2d(512,128,1,bias=False), nn.BatchNorm2d(128), nn.ReLU(inplace=True)) #[1, 128, 14, 14]
  60.         self.inception4c2 = nn.Sequential(nn.Conv2d(512,128,1,bias=False), nn.BatchNorm2d(128), nn.ReLU(inplace=True),
  61.                                          nn.Conv2d(128,256,3,1,1,bias=False), nn.BatchNorm2d(256), nn.ReLU(inplace=True))#[1, 256, 14, 14]
  62.         self.inception4c3 = nn.Sequential(nn.Conv2d(512,24,1,bias=False), nn.BatchNorm2d(24), nn.ReLU(inplace=True),
  63.                                          nn.Conv2d(24,64,5,1,2,bias=False), nn.BatchNorm2d(64), nn.ReLU(inplace=True)) #[1, 64, 14, 14]
  64.         self.inception4c4 = nn.Sequential(nn.MaxPool2d(kernel_size=3,stride=1,padding=1,ceil_mode=True), 
  65.                                          nn.Conv2d(512,64,1,bias=False), nn.BatchNorm2d(64), nn.ReLU(inplace=True)) #[1, 64, 14, 14]
  66.         
  67.         #inception 4d的输入：[1,512,14,14]   128+256+64+64=512
  68.         self.inception4d1 = nn.Sequential(nn.Conv2d(512,112,1,bias=False), nn.BatchNorm2d(112), nn.ReLU(inplace=True)) #[1, 112, 14, 14]
  69.         self.inception4d2 = nn.Sequential(nn.Conv2d(512,144,1,bias=False), nn.BatchNorm2d(144), nn.ReLU(inplace=True),
  70.                                          nn.Conv2d(144,288,3,1,1,bias=False), nn.BatchNorm2d(288), nn.ReLU(inplace=True))#[1, 288, 14, 14]
  71.         self.inception4d3 = nn.Sequential(nn.Conv2d(512,32,1,bias=False), nn.BatchNorm2d(32), nn.ReLU(inplace=True),
  72.                                          nn.Conv2d(32,64,5,1,2,bias=False), nn.BatchNorm2d(64), nn.ReLU(inplace=True)) #[1, 64, 14, 14]
  73.         self.inception4d4 = nn.Sequential(nn.MaxPool2d(kernel_size=3,stride=1,padding=1,ceil_mode=True), 
  74.                                          nn.Conv2d(512,64,1,bias=False), nn.BatchNorm2d(64), nn.ReLU(inplace=True)) #[1, 64, 14, 14]
  75.         
  76.         #aux2的输入：[1, 528, 14, 14]  112+288+64+64=528
  77.         self.aux2_f = nn.Sequential(nn.AvgPool2d(kernel_size=5, stride=3),   #[1, 528, 4, 4]
  78.                                  nn.Conv2d(528,128,1,bias=False), nn.BatchNorm2d(128), nn.ReLU(inplace=True)) #[1, 128, 4, 4]
  79.         self.aux2_c = nn.Sequential(nn.Linear(128*4*4, 1024), nn.ReLU(inplace=True), nn.Dropout(0.7), nn.Linear(1024, num_classes))
  80.         
  81.         #inception 4e的输入：[1, 528, 14, 14]  112+288+64+64=528
  82.         self.inception4e1 = nn.Sequential(nn.Conv2d(528,256,1,bias=False), nn.BatchNorm2d(256), nn.ReLU(inplace=True)) #[1, 256, 14, 14]
  83.         self.inception4e2 = nn.Sequential(nn.Conv2d(528,160,1,bias=False), nn.BatchNorm2d(160), nn.ReLU(inplace=True),
  84.                                          nn.Conv2d(160,320,3,1,1,bias=False), nn.BatchNorm2d(320), nn.ReLU(inplace=True))#[1, 320, 14, 14]
  85.         self.inception4e3 = nn.Sequential(nn.Conv2d(528,32,1,bias=False), nn.BatchNorm2d(32), nn.ReLU(inplace=True),
  86.                                          nn.Conv2d(32,128,5,1,2,bias=False), nn.BatchNorm2d(128), nn.ReLU(inplace=True)) #[1, 128, 14, 14]
  87.         self.inception4e4 = nn.Sequential(nn.MaxPool2d(kernel_size=3,stride=1,padding=1,ceil_mode=True), 
  88.                                          nn.Conv2d(528,128,1,bias=False), nn.BatchNorm2d(128), nn.ReLU(inplace=True)) #[1, 128, 14, 14]
  89.         
  90.         #maxpool的输入：[1, 832, 14, 14]   256+320+128+128=832
  91.         self.pool4 = nn.MaxPool2d(kernel_size=3,stride=2,ceil_mode=True) #[1, 832, 7, 7]
  92.         
  93.         #inception 5a 的输入：[1, 832, 7, 7]
  94.         self.inception5a1 = nn.Sequential(nn.Conv2d(832,256,1,bias=False), nn.BatchNorm2d(256), nn.ReLU(inplace=True)) #[1, 256, 7, 7]
  95.         self.inception5a2 = nn.Sequential(nn.Conv2d(832,160,1,bias=False), nn.BatchNorm2d(160), nn.ReLU(inplace=True),
  96.                                          nn.Conv2d(160,320,3,1,1,bias=False), nn.BatchNorm2d(320), nn.ReLU(inplace=True))#[1, 320, 7, 7]
  97.         self.inception5a3 = nn.Sequential(nn.Conv2d(832,32,1,bias=False), nn.BatchNorm2d(32), nn.ReLU(inplace=True),
  98.                                          nn.Conv2d(32,128,5,1,2,bias=False), nn.BatchNorm2d(128), nn.ReLU(inplace=True)) #[1, 128, 7, 7]
  99.         self.inception5a4 = nn.Sequential(nn.MaxPool2d(kernel_size=3,stride=1,padding=1,ceil_mode=True), 
  100.                                          nn.Conv2d(832,128,1,bias=False), nn.BatchNorm2d(128), nn.ReLU(inplace=True)) #[1, 128, 7, 7]
  101.         #inception5b 的输入：[1, 832, 7, 7]   256+320+128+128=832
  102.         self.inception5b1 = nn.Sequential(nn.Conv2d(832,384,1,bias=False), nn.BatchNorm2d(384), nn.ReLU(inplace=True)) #[1, 384, 7, 7]
  103.         self.inception5b2 = nn.Sequential(nn.Conv2d(832,192,1,bias=False), nn.BatchNorm2d(192), nn.ReLU(inplace=True),
  104.                                          nn.Conv2d(192,384,3,1,1,bias=False), nn.BatchNorm2d(384), nn.ReLU(inplace=True))#[1, 384, 7, 7]
  105.         self.inception5b3 = nn.Sequential(nn.Conv2d(832,48,1,bias=False), nn.BatchNorm2d(48), nn.ReLU(inplace=True),
  106.                                          nn.Conv2d(48,128,5,1,2,bias=False), nn.BatchNorm2d(128), nn.ReLU(inplace=True)) #[1, 128, 7, 7]
  107.         self.inception5b4 = nn.Sequential(nn.MaxPool2d(kernel_size=3,stride=1,padding=1,ceil_mode=True), 
  108.                                          nn.Conv2d(832,128,1,bias=False), nn.BatchNorm2d(128), nn.ReLU(inplace=True)) #[1, 128, 7, 7]
  109.         
  110.         #avgpool的输入：[1, 1024, 7, 7]   384+384+128+128=1024
  111.         self.feature = nn.AvgPool2d(kernel_size=7, stride=7)  #[1, 1024, 1, 1]
  112.         self.cla = nn.Sequential(nn.Dropout(0.4), nn.Linear(1024, num_classes))  #[1, 1000]
  113.  
  114.     def forward(self, x):
  115.         x = self.pool2(self.conv3(self.conv2(self.pool1(self.conv1(x)))))
  116.         in3a = torch.cat([self.inception3a1(x),self.inception3a2(x),self.inception3a3(x),self.inception3a4(x)], dim=1)
  117.         in3b = torch.cat([self.inception3b1(in3a),self.inception3b2(in3a),self.inception3b3(in3a),self.inception3b4(in3a)], dim=1)
  118.         mp1 = self.pool3(in3b)
  119.         in4a = torch.cat([self.inception4a1(mp1),self.inception4a2(mp1),self.inception4a3(mp1),self.inception4a4(mp1)], dim=1)
  120.         in4b = torch.cat([self.inception4b1(in4a),self.inception4b2(in4a),self.inception4b3(in4a),self.inception4b4(in4a)], dim=1)
  121.         in4c = torch.cat([self.inception4c1(in4b),self.inception4c2(in4b),self.inception4c3(in4b),self.inception4c4(in4b)], dim=1)
  122.         in4d = torch.cat([self.inception4d1(in4c),self.inception4d2(in4c),self.inception4d3(in4c),self.inception4d4(in4c)], dim=1)
  123.         in4e = torch.cat([self.inception4e1(in4d),self.inception4e2(in4d),self.inception4e3(in4d),self.inception4e4(in4d)], dim=1)
  124.         mp2 = self.pool4(in4e)
  125.         in5a = torch.cat([self.inception5a1(mp2),self.inception5a2(mp2),self.inception5a3(mp2),self.inception5a4(mp2)], dim=1)
  126.         in5b = torch.cat([self.inception5b1(in5a),self.inception5b2(in5a),self.inception5b3(in5a),self.inception5b4(in5a)], dim=1)
  127.         avgpool = self.feature(in5b).view(-1, 1024*1*1)
  128.         output = self.cla(avgpool)
  129.         aux1 = self.aux1_c(self.aux1_f(in4a).view(-1, 128*4*4))
  130.         aux2 = self.aux2_c(self.aux2_f(in4d).view(-1, 128*4*4))
  131.         return output, aux1, aux2
  132.         
  133. data = torch.ones(1, 3, 224, 224)
  134. net2 = Googlenet(num_classes=1000)
  135. output, aux1, aux2 = net2(data)
  136. output.shape, aux1.shape, aux2.shape
  137. summary(net2, (1, 3, 224, 224), device='cpu', depth=1)   #depth表示显示架构的层级，=1表示显示一层


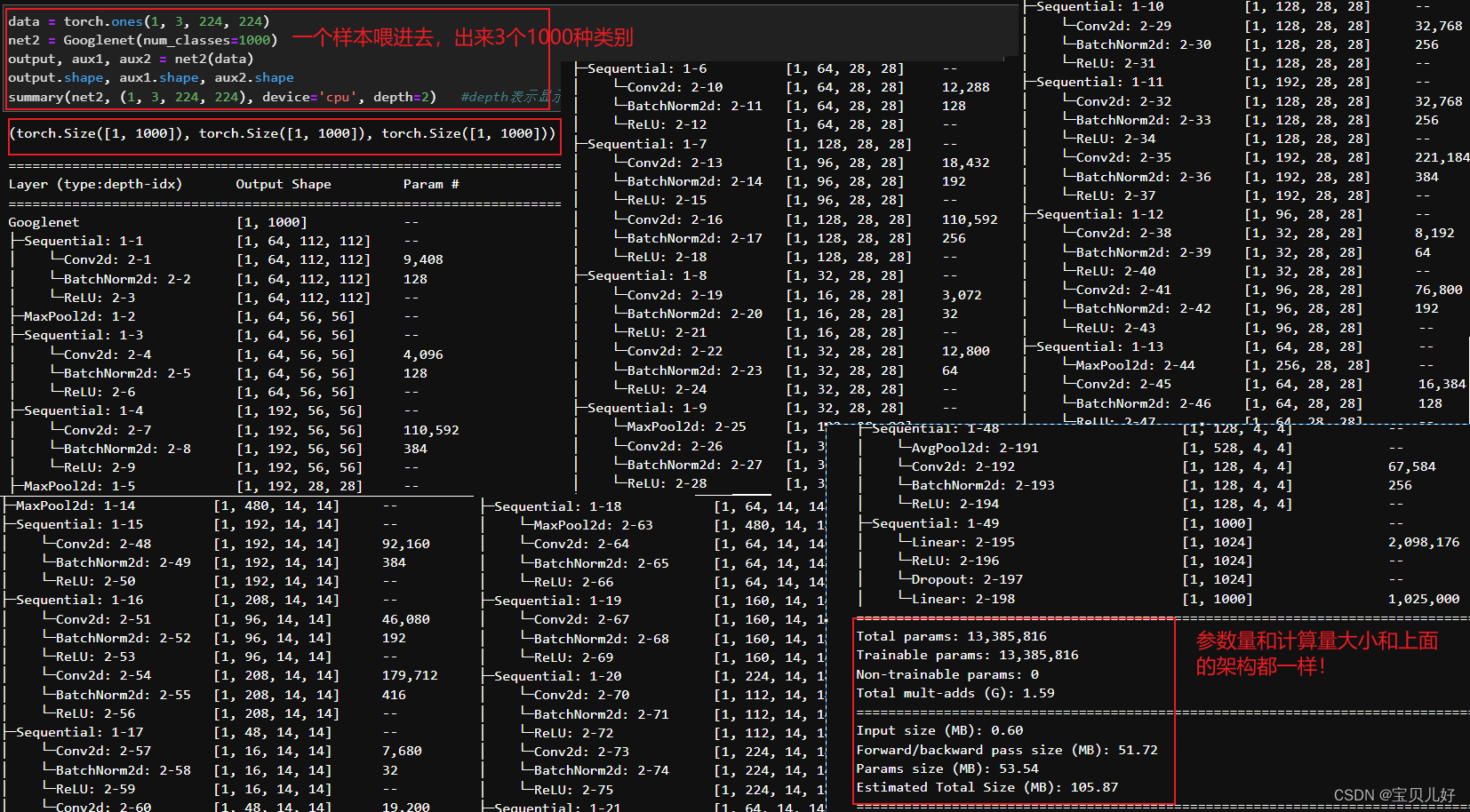
由于summary是把所有的层都显示出来了，所以看着层非常多的样子，其实大家都说googlenet只有22层，因为BN层不算、relu层不算、dropout也不算、池化层也不算。只算卷积层和线性层统计在模型层数之内。虽说这种统计方式很搞笑，anyway,这不重要，重要的是它的参数总共才有13,385,816个，其中有7百多万个参数还是三个分类器线性层上的参数量。每个inception块儿上的参数量就微乎其微了。所以Googlenet的参数量和计算量都是碾压VGG的，所以在2014年的ILSVRC上，googlenet虽然只以微小的优势打败了VGG(好像是比VGG高出0.6个百分点)，但其计算效率和在架构上的革新是一个时代的新标志。此后学者们对inception块儿和Googlenet整体排布都进行了许多改进，其中一个经典就是inceptionV3。V3虽然使用的仍是inception的基本思路，但其inception块儿中的具体分支以及整体架构都发生了巨大变化，在经过适当的训练后，V3可以在imagenet2012年数据集上跑出4.2%的错误率。此后的V4更是可以达到3%的错误率。至此，incepton一族就成了效果仅次于深层残差网络(100层以上) 的浅层架构。

至此，我们就完成了对GoogLeNet架构上的复现，也就是我们输入网络1个样本，就会出来3个1000个数字。注意这里的3个结果都不是softmax输出！后面要开始训练这个模型，你得先对这个3个1000个数字进行softmax处理，然后才是构造损失函数进行训练。

声明：本文内容由网友自发贡献，不代表【wpsshop博客】立场，版权归原作者所有，本站不承担相应法律责任。如您发现有侵权的内容，请联系我们。转载请注明出处：https://www.wpsshop.cn/w/不正经/article/detail/479889
推荐阅读
相关标签

Copyright © 2003-2013 www.wpsshop.cn 版权所有，并保留所有权利。

  

闽ICP备14008679号