数据结构——二叉树练习（深搜广搜）

我们今天来看二叉树的习题：

路径之和

https://leetcode.cn/problems/path-sum-ii/

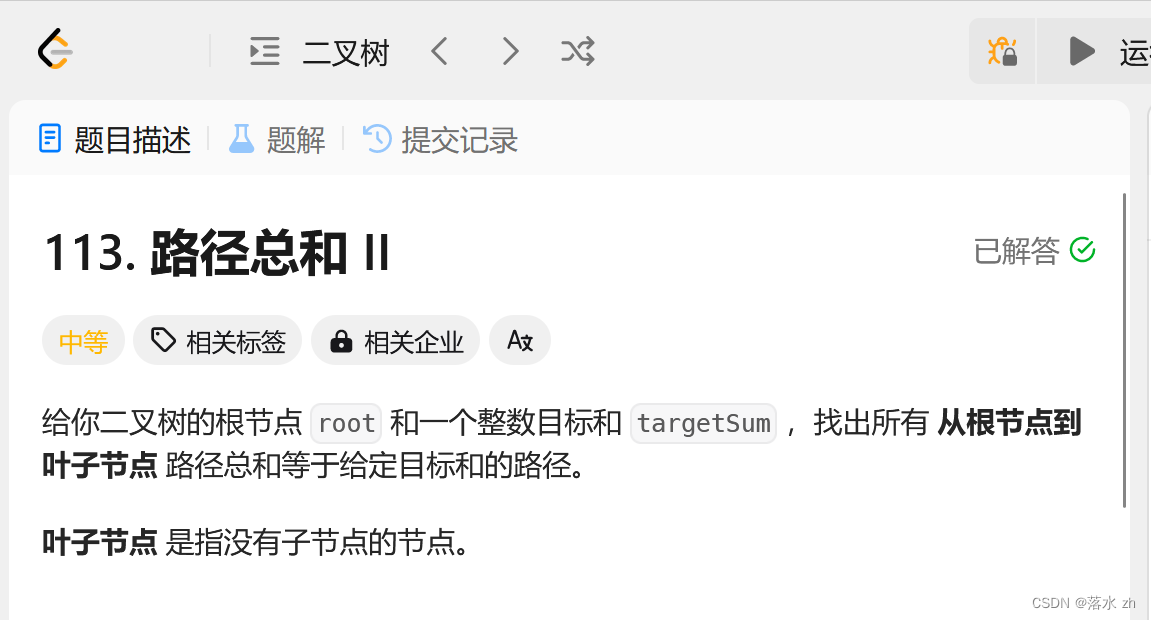
这是一个典型的回溯，深度优先算法的题，这里我们来简单的介绍一下深度优先算法和广度优先算法：

深度优先算法和广度优先算法

深度优先搜索（Depth-First Search, DFS）和广度优先搜索（Breadth-First Search, BFS）是两种常用的图（或树）遍历算法。虽然它们都是用于探索图中所有节点的策略，但在搜索顺序和所需数据结构上有所不同。

深度优先搜索（DFS）

深度优先搜索是一种沿着图的深度方向尽可能深地搜索的算法。它会优先访问离起点最近的未访问节点的子节点，直到到达叶子节点（没有子节点的节点）或无法继续深入为止，然后回溯到上一个节点，尝试访问其未被访问的另一个子节点，重复这一过程，直到图中所有节点都被访问过。

实现方式：

• 递归实现：从某个起始节点开始，递归地访问其未访问过的子节点。
• 栈实现：使用栈来保存待访问节点，每次从栈顶取出一个节点，访问它，并将其未访问过的子节点压入栈中。

广度优先搜索（BFS）

广度优先搜索是一种从起点开始，按层次逐层向外遍历的算法。它会先访问与起点距离最近的所有节点（即邻居节点），然后再访问这些节点的邻居节点，以此类推，直到遍历到目标节点或遍历完整个图。

实现方式：

• 队列实现：使用队列来保存待访问节点，每次从队头取出一个节点，访问它，并将其未访问过的邻居节点加入队尾。

比较

• 搜索顺序：

  • DFS：沿着一条路径深入到底，再回溯并尝试另一条路径，类似“纵深”探索。
  • BFS：从起点开始，逐层向外扩散，类似于“地毯式”搜索。

• 所需数据结构：

  • DFS：递归实现时不需要额外数据结构；栈实现时需用到栈。
  • BFS：需要使用队列。

• 空间复杂度：

  • DFS：递归实现的空间复杂度取决于递归调用的深度，最坏情况下可能达到O(n)；栈实现的空间复杂度为O(n)，n为图中节点数。
  • BFS：空间复杂度为O(n)，需要存储所有待访问节点。

• 适用场景：

  • DFS：适用于寻找图中是否存在某条路径、求解最短路径问题（无权图）等，特别是在高度大于宽度的图中效果较好。
  • BFS：适用于求解最短路径问题（有权图需使用Dijkstra算法或A*算法等）、寻找两个节点间的最短路径、拓扑排序等问题，特别是在宽度大于高度的图中效果较好。

我们今天这道题就是一个深度优先搜索，我们拿这棵树来举例子：

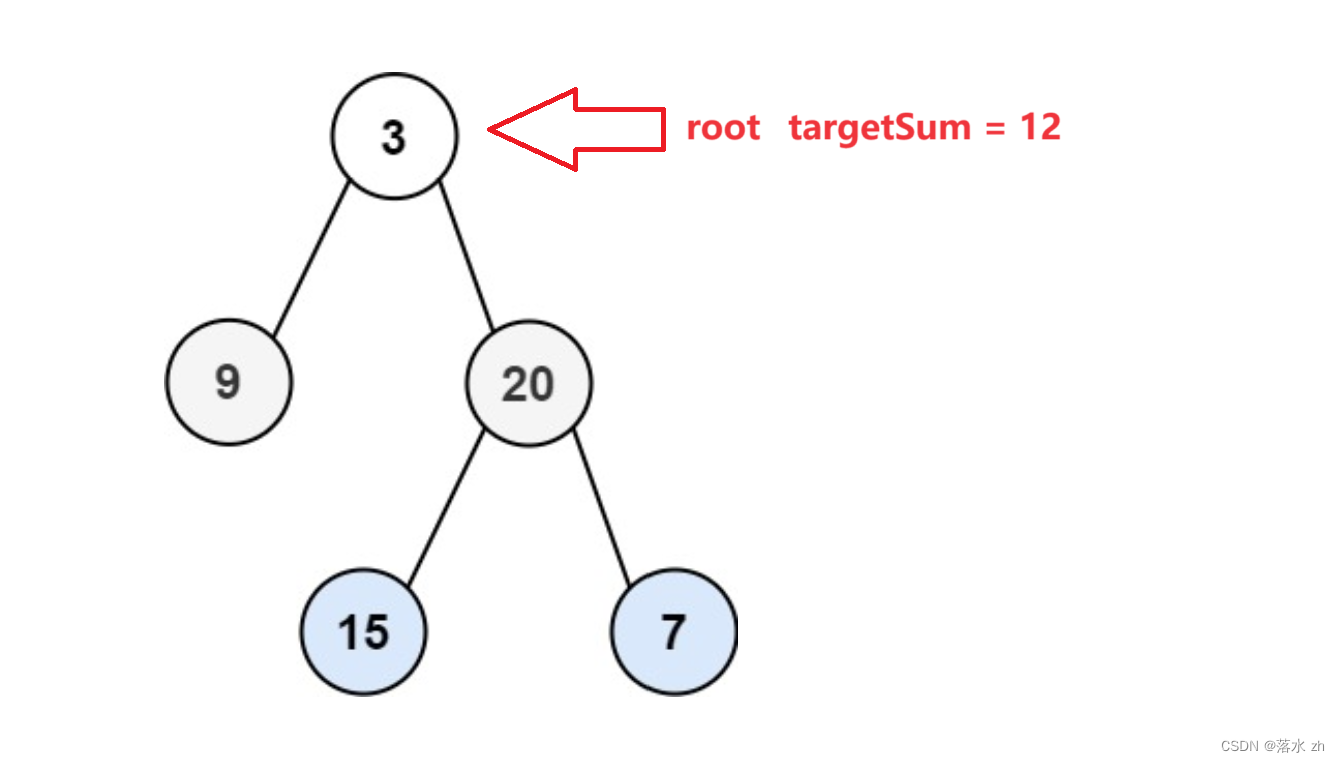
我们用二维vector来存放满足条件的路径：

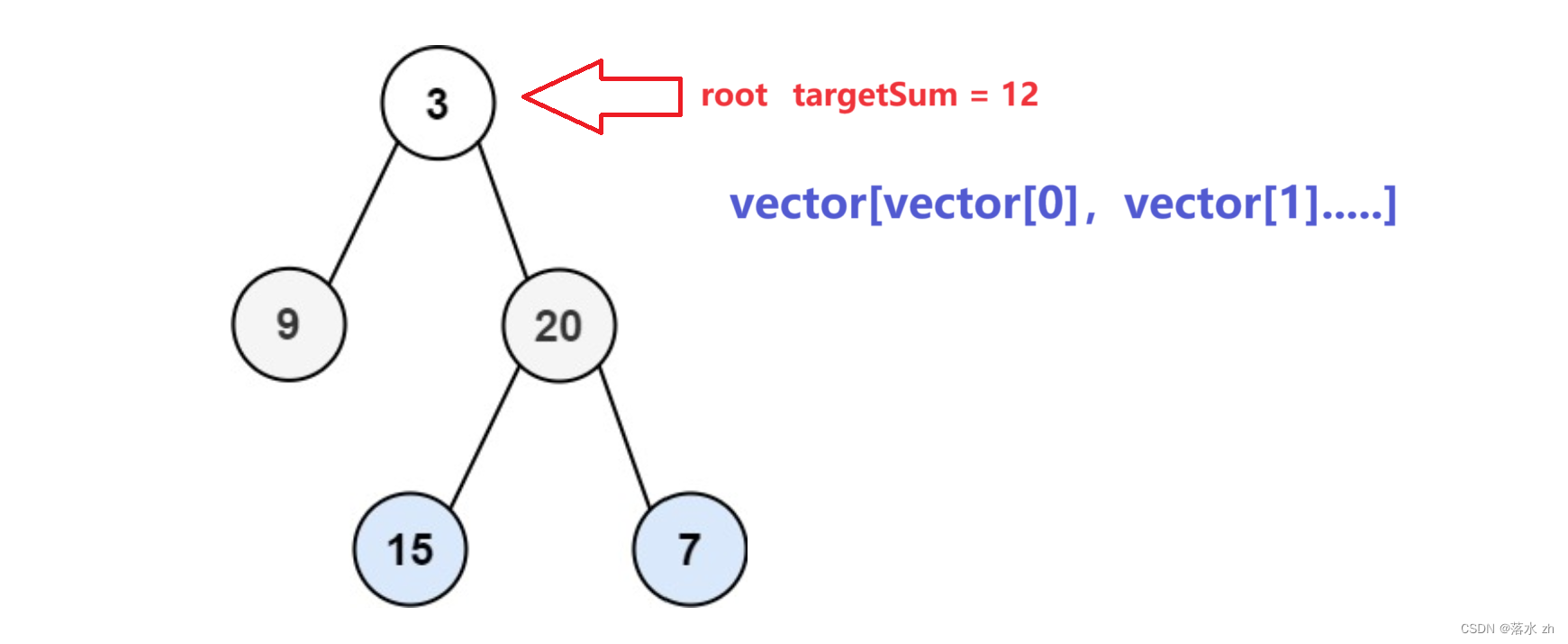
我们从3开始，先往左走，到9：

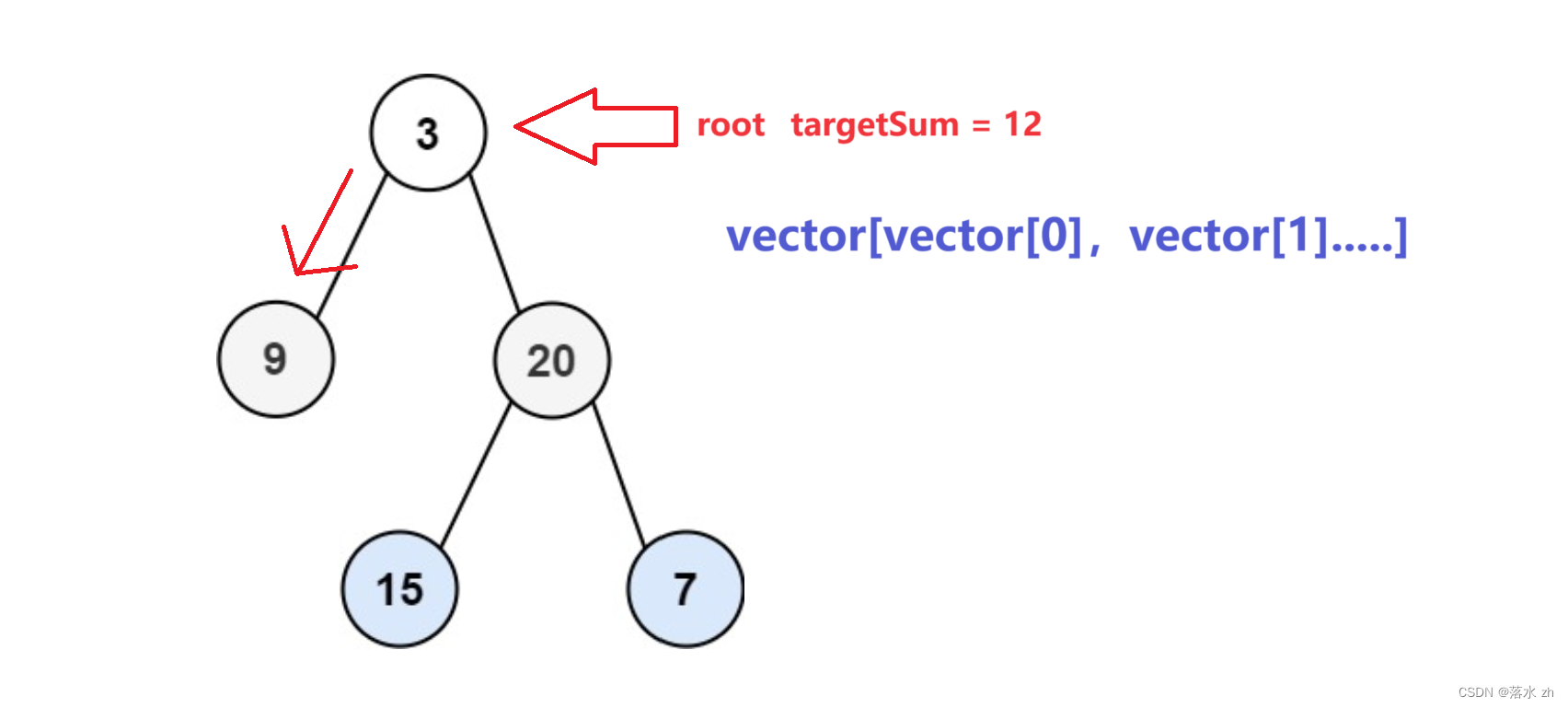
3 + 9 = 12故将3和9放入vector[0]中：

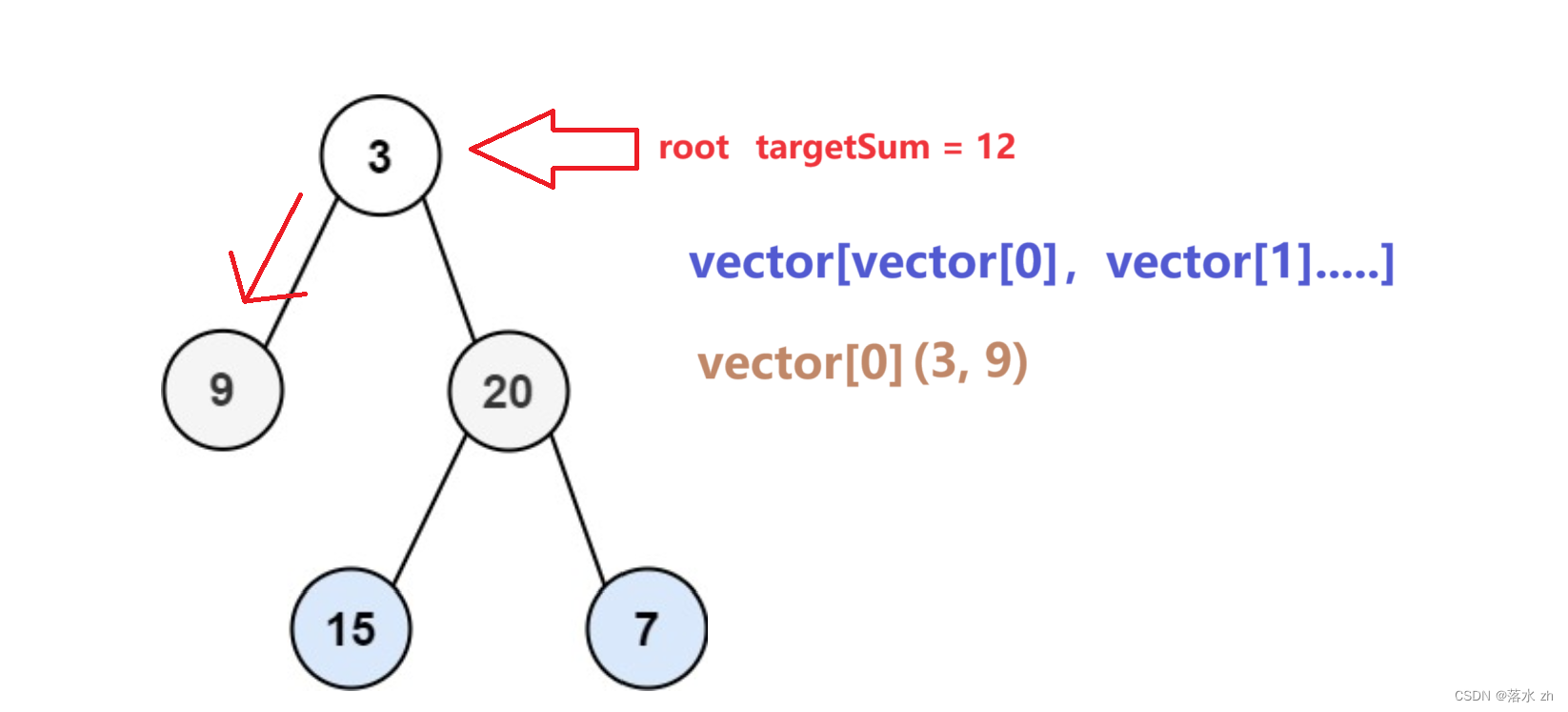
这个时候，往回走，回到3：
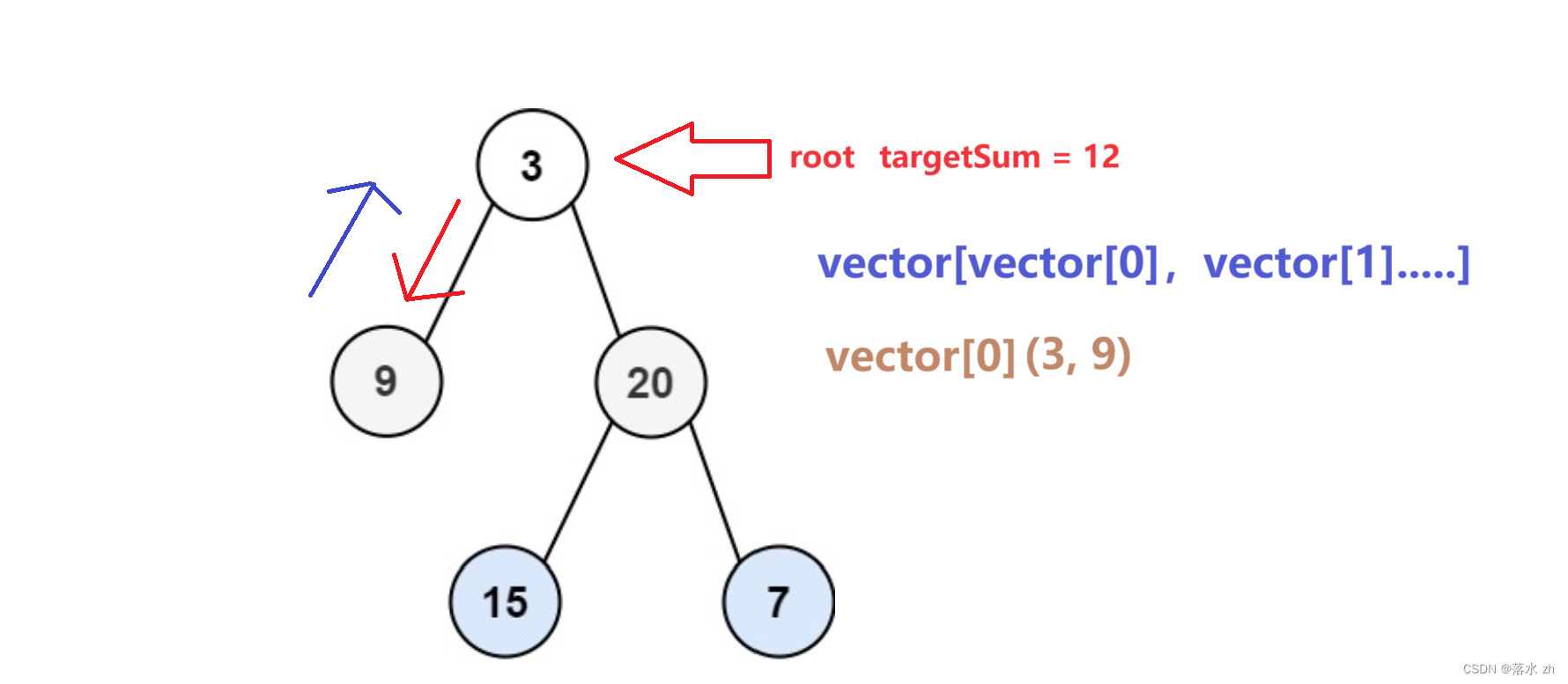回到3，便往右走：

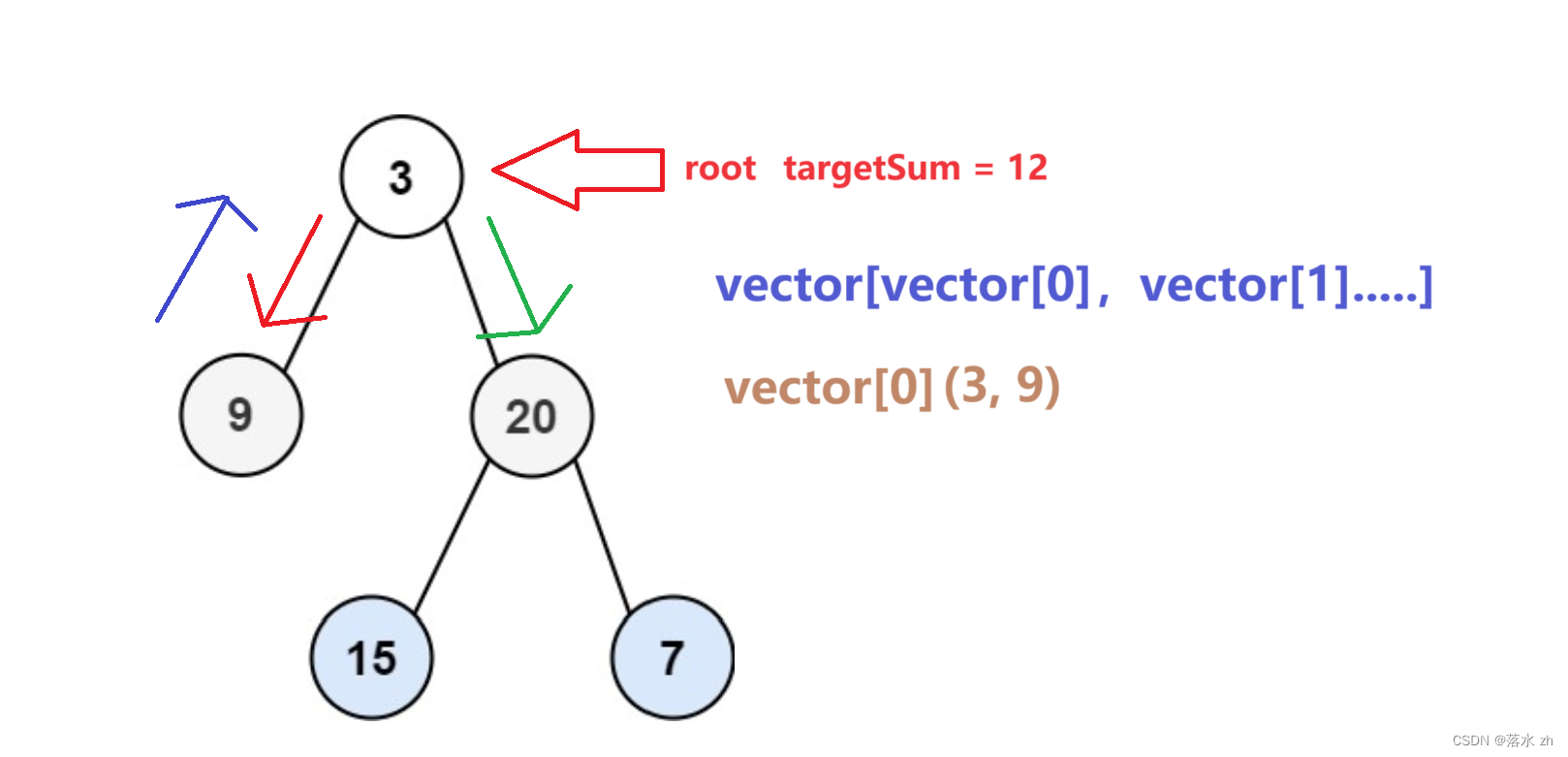
重复上述步骤，整理思路可得代码：

class Solution {
public:
	// 定义一个成员函数 dfs，用于实现深度优先搜索，查找所有和为目标值的路径
	void dfs(TreeNode* root, vector<int>& path, vector<vector<int>>& result,
	         int targetSum)
	{
	    // 如果当前节点为空，直接返回
	    if (root == nullptr)
	    {
	        return;
	    }
	
	    // 将当前节点的值加入路径，并从目标和中减去该值
	    path.push_back(root->val);
	    targetSum -= root->val;
	
	    // 如果当前节点是叶子节点（无左右子节点），且剩余目标和为0，说明找到了一条符合条件的路径
	    if (root->left == nullptr && root->right == nullptr && targetSum == 0)
	    {
	        result.push_back(path); // 将当前路径加入结果集
	    }
	
	    // 递归遍历左子树
	    dfs(root->left, path, result, targetSum);
	
	    // 递归遍历右子树
	    dfs(root->right, path, result, targetSum);
	
	    // 回溯：从路径中移除当前节点的值，以便于后续节点的搜索
	    path.pop_back();
	}
	
	// 定义一个成员函数 pathSum，用于查找二叉树中所有和为目标值的路径
	vector<vector<int>> pathSum(TreeNode* root, int targetSum)
	{
	    // 初始化结果容器，用于存放所有和为目标值的路径
	    vector<vector<int>> result;
	
	    // 初始化当前路径向量
	    vector<int> path; // 当前路径
	
	    // 调用 dfs 函数，从根节点开始搜索
	    dfs(root, path, result, targetSum);
	
	    // 返回找到的所有和为目标值的路径
	    return result;
	}
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48

二叉搜索树

二叉搜索树（Binary Search Tree, BST）是一种特殊类型的二叉树，它具有以下关键属性：

定义与性质：

有序性：对于二叉搜索树中的任意节点，其左子树中所有节点的值都严格小于该节点的值，而右子树中所有节点的值都严格大于该节点的值。这保证了树中的数据按照某种顺序排列。
递归结构：二叉搜索树的每个子节点（如果存在）本身也是一个二叉搜索树，也就是说，整个数据结构具有递归性质。

我们之前自己实现的二叉树就是二叉搜索树，如果还有小伙伴不怎么熟悉的，可以点击这里：

https://blog.csdn.net/qq_67693066/article/details/138163494

有一个重要的性质：二叉树的中序遍历是一个递增的数列，这个用来判断搜索二叉树是一个非常关键的方法。

判断一棵二叉树是否为搜索二叉树和完全二叉树

https://www.nowcoder.com/practice/f31fc6d3caf24e7f8b4deb5cd9b5fa97?tpId=196&tqId=37156&ru=/exam/oj

我们可以利用二叉搜索树中序遍历的特点来判断是否为二叉搜索树，判断是否为完全二叉树，这里我们就可以借助队列，用广度优先搜索：

假设我们有一棵完全二叉树：

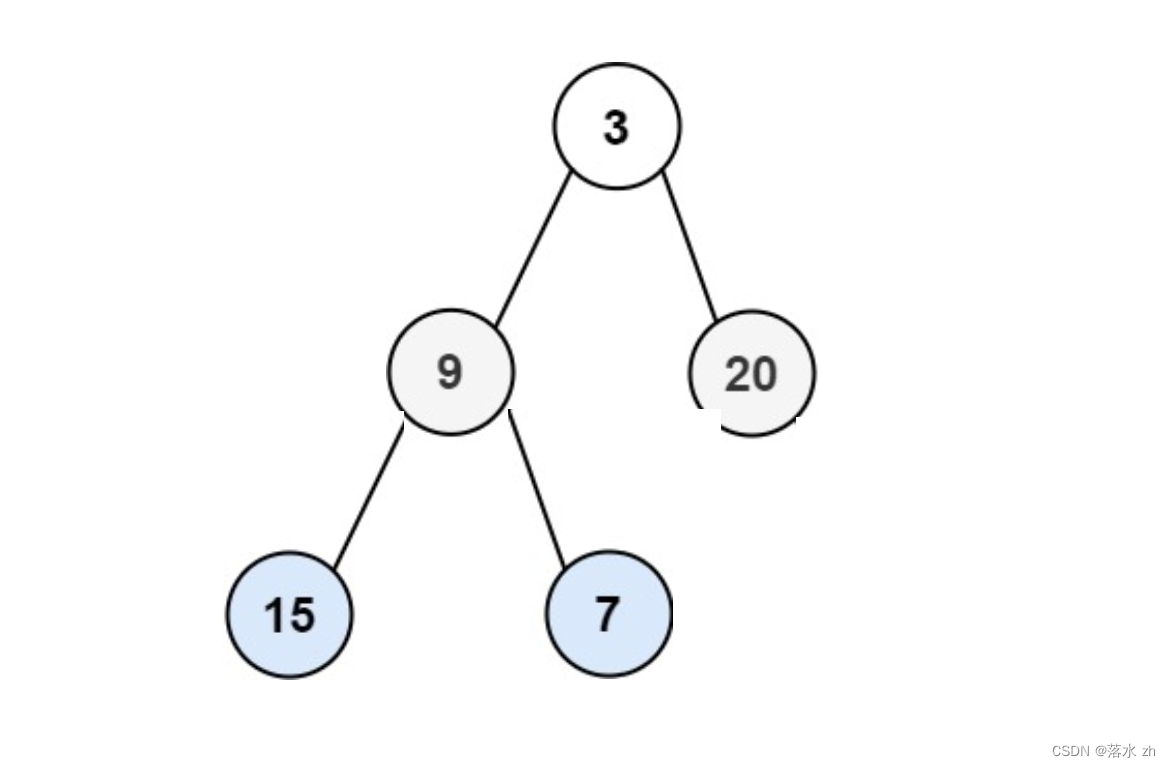
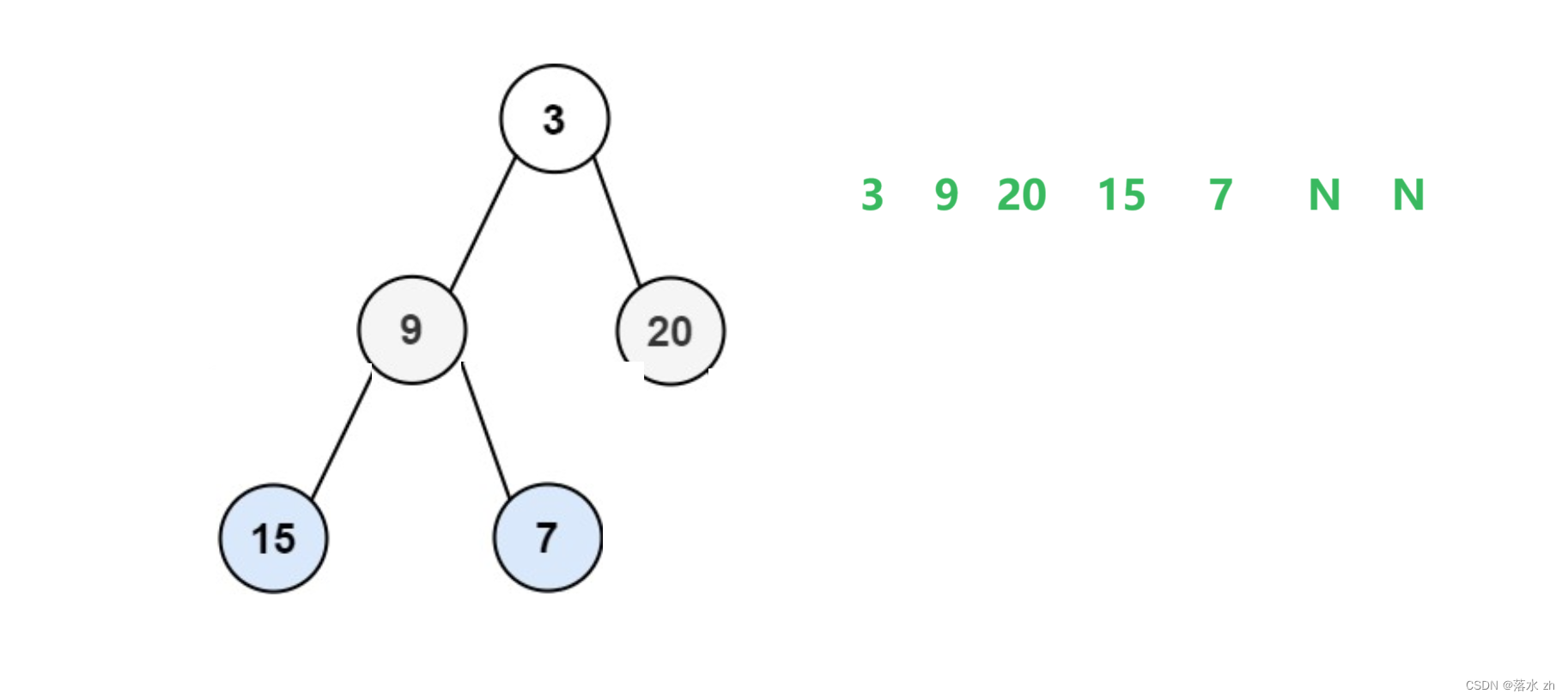
如果利用队列，全部放在队列中，应该是这样的顺序：

如果是非完全二叉树：

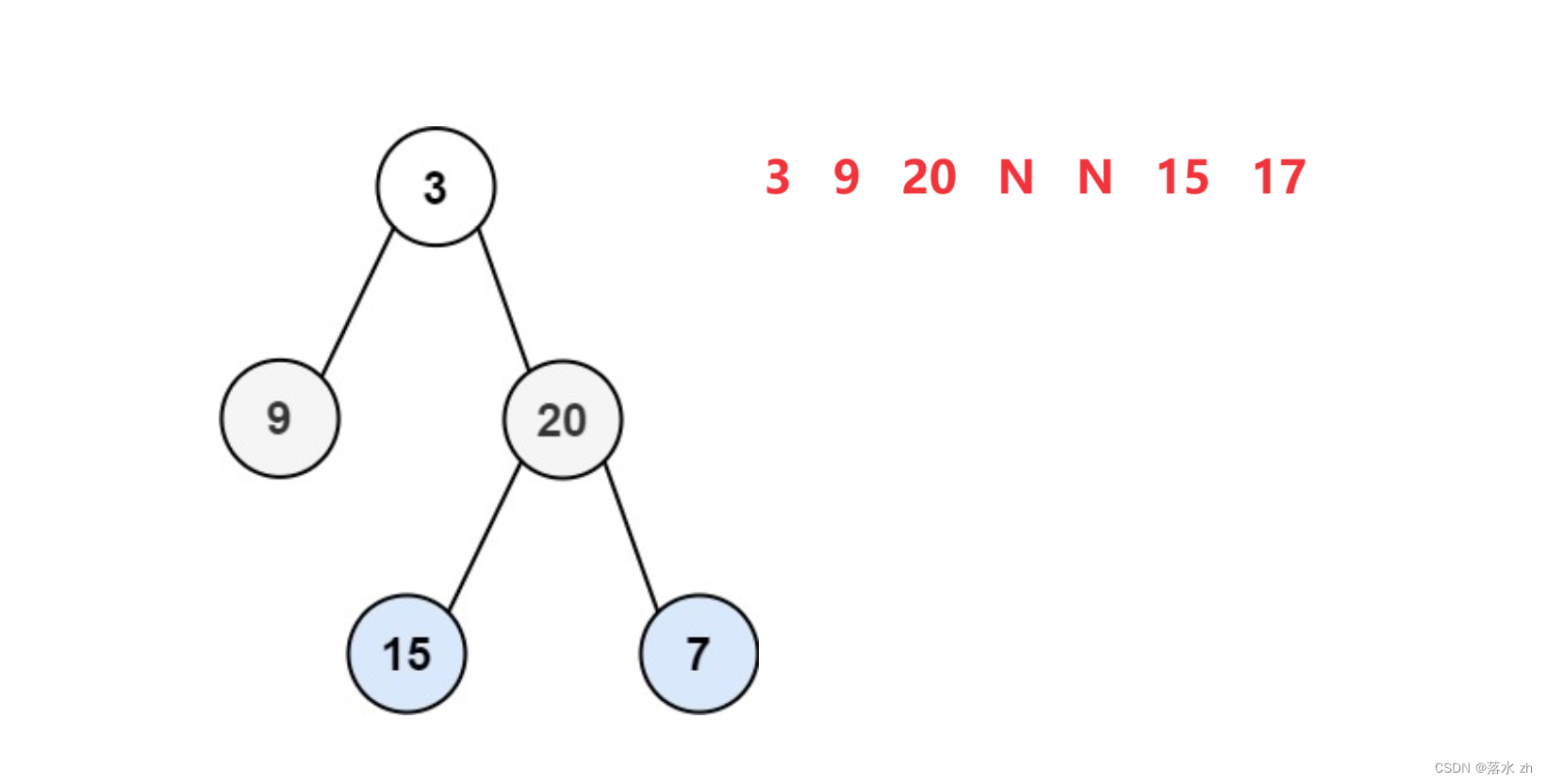
我们发现，如果是完全二叉树，那么空节点应该全都集中在末尾，如果是非完全二叉树，中间就会出现空结点，所以我们只要在遇到空结点时，检查之后是否有结点，如果没有就是完全二叉树，有的话就是非完全二叉树。

// 定义一个成员函数 judgeCompelte，用于判断给定的二叉树是否为完全二叉树
bool judgeCompelte(TreeNode* root)
{
    // 初始化一个队列，用于按层遍历二叉树
    queue<TreeNode*> queue;

    // 如果根节点不为空，将其入队
    if (root)
        queue.push(root);

    // 使用队列进行层序遍历
    while (!queue.empty())
    {
        // 弹出队首节点
        TreeNode* front = queue.front();
        queue.pop();

        // 如果遇到空节点，表示已经到达当前层的最后一个有效节点，跳出循环
        if (front == nullptr)
            break;

        // 将当前节点的左右子节点（无论是否为空）依次入队，准备遍历下一层
        queue.push(front->left);
        queue.push(front->right);
    }

    // 遍历结束后，队列中剩余的节点应全为空，因为它们对应于完全二叉树中不存在的节点
    // 如果队列中还有非空节点，说明这不是完全二叉树，返回false
    while (!queue.empty())
    {
        TreeNode* front = queue.front();
        queue.pop();

        if (front)
        {
            return false;
        }
    }

    // 队列已清空，且所有弹出的节点都符合完全二叉树的条件，返回true，表示给定二叉树是完全二叉树
    return true;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42

判断是否为二叉搜索树：

// 中序遍历二叉树，并将遍历结果存储在给定的向量中
void inorder(TreeNode* root, vector<int>& vc) {
    if (root == nullptr) {
        return;
    }

    inorder(root->left, vc); // 遍历左子树
    vc.push_back(root->val); // 将当前节点的值添加到向量中
    inorder(root->right, vc); // 遍历右子树
}

// 判断给定的二叉树是否为二叉搜索树
bool isBST(TreeNode* root) {
    vector<int> vc;
    inorder(root, vc); // 对二叉树进行中序遍历

    for (int i = 0; i < vc.size() - 1; i++) {
        if (vc[i] >= vc[i + 1]) { // 如果当前元素大于或等于下一个元素，则不是二叉搜索树
            return false;
        }
    }

    return true; // 如果所有元素都小于下一个元素，则是二叉搜索树
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24

那么这道题就可以迎刃而解了：

/**
 * struct TreeNode {
 *	int val;
 *	struct TreeNode *left;
 *	struct TreeNode *right;
 *	TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 * };
 */
class Solution {
public:
    //判断完全是否为完全二叉树
    bool judgeCompelte(TreeNode* root)
    {
        //初始化队列
        queue<TreeNode*> queue;

        //入队
        if(root)
            queue.push(root);

    
        while(!queue.empty())
        {
            TreeNode* front = queue.front();
            queue.pop();

            if(front == nullptr)
                break;
            
            queue.push(front->left);
            queue.push(front->right);
            
        }

        while(!queue.empty())
        {
           TreeNode* front = queue.front();
           queue.pop();

            if (front)
            {
                return false;
            }
        }

        return true;
    }

    //中序遍历
    void inoder(TreeNode* root,vector<int>& vc)
    {
        if(root == nullptr)
        {
            return;
        }

        inoder(root->left,vc);
        vc.push_back(root->val);
        inoder(root->right,vc);
    }

    
    //判断
    vector<bool> judgeIt(TreeNode* root) 
    {
       vector<bool> result(2,false); 
       if(!root)
       {
            result[0] = true;
            result[1] = true;
            return result;
       }

       //判断是否为二叉搜索树
       vector<int> vc;
       inoder(root,vc);
       result[0] = true;

       for(int i = 0; i <vc.size() - 1; i++)
       {
            if(vc[i] >= vc[i+1])
            {
                result[0] = false;
                break;
            }
       }

       //判断是否为完全二叉树
      result[1] = judgeCompelte(root);

       return result; 
    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93