平衡二叉搜索树--AVL详解剖析_avl数

目录

一、什么是AVL树

二、AVL树的作用

三、树节点的定义

四、节点的插入

五、旋转

1.左单旋

2.右单旋

左右双旋代码 ：

4.右左双旋

---

一、什么是AVL树

AVL树就是二叉搜索树的进一步的优化，二叉搜索树虽可以缩短查找的效率，但是当数据有序或接近有序二叉搜索树变成单支树，在查找的过程中其效率会变得更低下。所以有一种可以达到自平衡二叉搜索树（AVL），它在每次插入或删除节点时会通过平衡因子（高度差）来进行旋转操作保持树的平衡。AVL树的名称来自它的发明者G. M. Adelson-Velsky和E. M. Landis。

AVL树的特点：

1. AVL树的平衡受到平衡因子（高度差）的影响，对于任意节点，其左子树和右子树的高度差不超过1。如果一棵二叉搜索树是高度平衡的，它就是AVL树。如果它有n个结点，其高度可保持在O(log n)，搜索时间复杂度O(log n）
2. 当向AVL树中插入或删除节点时，就会存在树的平衡性被破坏的可能。所以，为了恢复平衡，AVL树使用四种旋转操作：左旋、右旋、左右旋和右左旋。通过这些旋转操作，AVL树可以在O(log n)时间内完成插入和删除操作，并保持树的平衡。
3. 因为AVL树保持严格的平衡，因此其在查找、插入和删除操作上的时间复杂度都是O(log n)，使得它成为一种高效的数据结构。

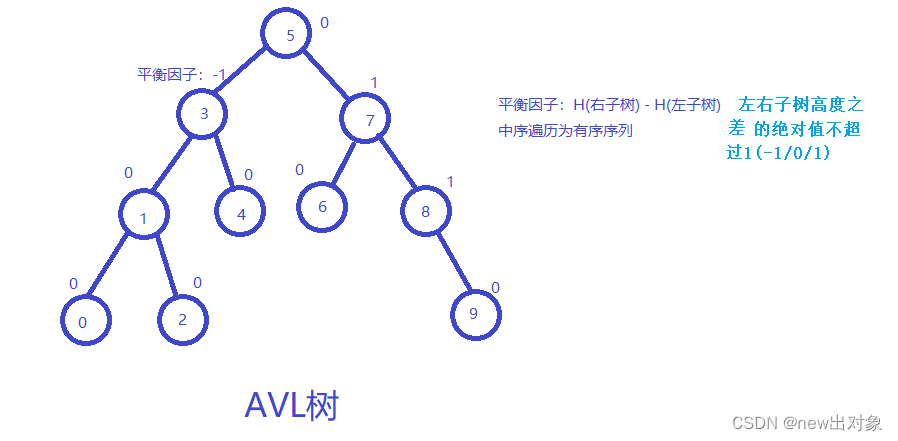
二、AVL树的作用

1.  提供高效的查找操作：AVL树的平衡性保证了在最坏情况下，查找操作的时间复杂度为O(log n)，其中n是树中节点的数量。这使得AVL树在需要频繁查找元素的场景下非常有用，例如数据库索引、字典等。
2. 支持有序遍历：由于AVL树是一种二叉搜索树，其节点按照特定的顺序进行排列。因此，通过对AVL树进行中序遍历，可以按照升序或降序获取树中的所有元素。这使得AVL树在需要按顺序处理数据的场景下很有用，例如范围查询、排序等。
3. 动态数据集的维护：AVL树的自平衡性适用于动态数据集的维护。当插入或删除节点时，AVL树会通过旋转操作来保持平衡，从而保证树的高度始终保持在O(log n)的范围内。这使得AVL树在需要频繁地插入和删除元素的场景下表现出色，例如实时的数据更新、动态排序等。
4. 实现其他数据结构：AVL树也可以作为其他数据结构的基础，例如集合、映射、优先队列等。通过在AVL树上实现相应的操作，可以实现这些数据结构，并且保证其在插入、删除和查找等操作上的高效性和平衡性。

三、树节点的定义

template<class K, class V>
struct AVLTreeNode
{
	AVLTreeNode<K, V>* _left;  //左子节点
	AVLTreeNode<K, V>* _right;  //右子节点
	AVLTreeNode<K, V>* _parent;  //父亲节点
	pair<K, V> _kv;  // 用于存储节点值
	int _bf;  // 平衡因子
 
	AVLTreeNode(const pair<K, V>& kv)//初始化构造
		:_left(nullptr)
		, _right(nullptr)
		, _parent(nullptr)
		, _kv(kv)
		, _bf(0)
	{}
 
}
 
typedef AVLTreeNode<K, V> Node;

四、节点的插入

AVL树的插入主要分为两点：

1.根据二叉搜索树的性质进行插入新的节点

   二叉搜索树性质：

• 若它的左子树不为空，则左子树上所有节点的值都小于根节点的值
• 若它的右子树不为空，则右子树上所有节点的值都大于根节点的值
• 它的左右子树也分为二叉搜索树

2.调整节点的平衡因子

调整规则：（parent表示的是插入后的节点的父亲节点）

1、新增在右，父节点的平衡因子parent->bf++;新增在左，父节点的平衡因子parent->bf--;

2、更新后，如果parent->bf== 1 或-1，说明parent插入前的平衡因子是0，左右子树高度相等，插入后有一边高，parent高度变了，所以需要继续更新上面节点的 bf

3、更新后，如果parent->bf ==0，说明parent插入前的平衡因子是1 或 -1，左右子树一边高一边低，插入后两边一样高，插入填上了矮了那边，parent所在子树高度不变，不需要继续往上更新

4、更新后，如果parent-> bf== 2 或 -2，说明parent插入前的平衡因子是1 或 -1，是平衡临界值，插入后变成2 或 -2，打破了平衡，parent所在子树需要根据实际情况进行旋转处理。

5、更新后，如果parent->bf > 2 或 <-2的值，则说明插入前就不是AVL树，需要去检查之前操作的问题。

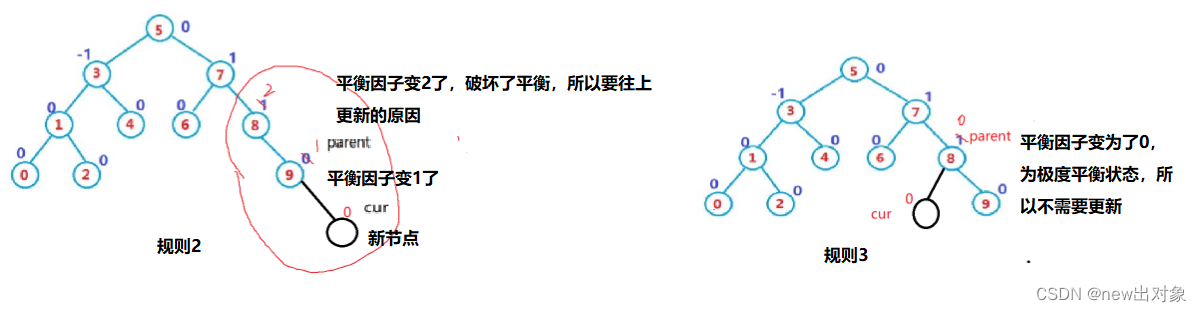
插入代码讲解：

bool Insert(const pair<K, V>& kv)
	{
		if (_root == nullptr)//如果是空树，插入的节点就是根节点
		{
			_root = new Node(kv);
			return true;
		}
 
//parent用于记录cur节点的父亲节点，防止在插入新节点时丢失
		Node* parent = nullptr;
		Node* cur = _root;
// 遍历找到插入新节点的位置，parent记录该位置，cur节点用于探索后面的节点或存储新节点便于插入
		while (cur)  
		{
			if (cur->_kv.first < kv.first)
			{
				parent = cur;
				cur = cur->_right;
			}
			else if (cur->_kv.first > kv.first)
			{
				parent = cur;
				cur = cur->_left;
			}
			else  //一般不可能出现相等的情况，出现了则说明该搜索二叉树构建存在问题
			{
				return false;
			}
		}
//cur作为新节点，通过parent与该树进行连接，完成节点插入
		cur = new Node(kv);
		if (parent->_kv.first < kv.first)
		{
			parent->_right = cur;
		}
		else
		{
			parent->_left = cur;
		}
 
		cur->_parent = parent;
 
		// 控制平衡
		// 更新平衡因子
        //根据上面的调整规则更新平衡因子
		while (parent)
		{
            //规则1
			if (cur == parent->_right)
			{
				parent->_bf++;
			}
			else
			{
				parent->_bf--;
			}
            //规则3
			if (parent->_bf == 0)
			{
				break;
			}
            //规则2
			else if (abs(parent->_bf) == 1)
			{
				parent = parent->_parent;
				cur = cur->_parent;
			}
            //规则4
			else if (abs(parent->_bf) == 2)
			{
				// 说明parent所在子树已经不平衡了，需要旋转处理
				if (parent->_bf == 2 && cur->_bf == 1)
				{
					RotateL(parent);  //左单旋
				}
				else if ((parent->_bf == -2 && cur->_bf == -1))
				{
					RotateR(parent);  //右单旋
				}
				else if (parent->_bf == -2 && cur->_bf == 1)
				{
					RotateLR(parent);  // 左右双旋
				}
				else if (parent->_bf == 2 && cur->_bf == -1)
				{
					RotateRL(parent);  // 右左双旋 
				}
				else
				{
					assert(false);
				}
 
				break;
			}
            //规则5不存在的可能
			else
			{
				assert(false);
			}
		}
 
		return true;
	}

五、旋转

1.左单旋

旋转原因：

在插入新节点后，父节点parent->bf==2，子节点cur->bf==1。也就是在插入前，该节点bf=1，插入后bf=2，是在该节点的右子树进行插入。如下图：

subR：parent的右子节点

subRL：parent的右子节点的左节点

旋转后subRL的父亲节点，要由原来的subR变为parent节点。subR节点，就变为新的parent节点

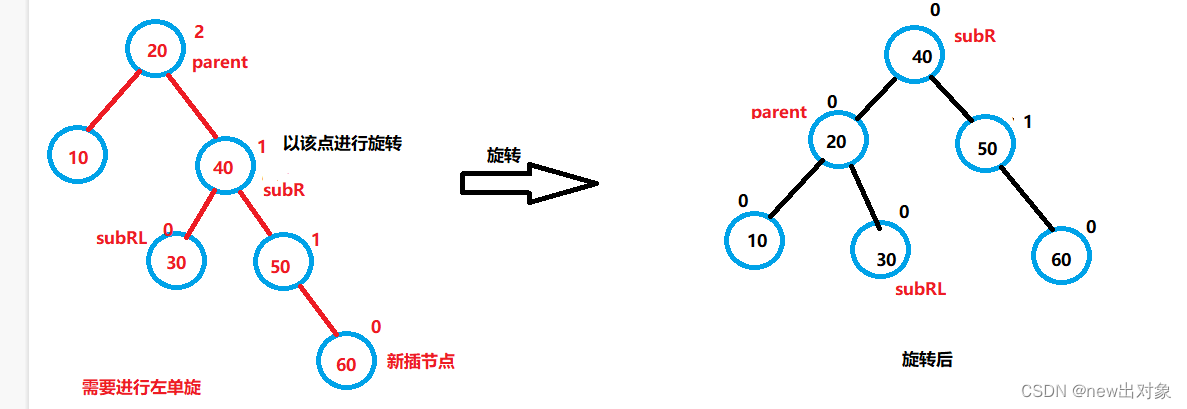
 左单旋代码：

	void RotateL(Node* parent)
	{
		Node* subR = parent->_right;
		Node* subRL = subR->_left;
 
        //将原来的subRL节点的父亲节点指向为parent
		parent->_right = subRL;
		if (subRL)
			subRL->_parent = parent;
 
        //记录当前parent节点的父节点，保证旋转后，能与主树连接上
		Node* ppNode = parent->_parent;
 
        //将subR变为新的parent节点
		subR->_left = parent;
		parent->_parent = subR;
 
        //将旋转后的子树与原来的主树进行连接
		if (_root == parent)
		{
			_root = subR;
			subR->_parent = nullptr;
		}
		else
		{
            //判断该子树是原来主树的左子树还是右子树，在进行连接
			if (ppNode->_left == parent)
			{
				ppNode->_left = subR;
			}
			else
			{
				ppNode->_right = subR;
			}
 
			subR->_parent = ppNode;
		}
}

2.右单旋

旋转原因:

parent->bf==-2,cur->bf==-1

在parent的左子树左节点上进行插入

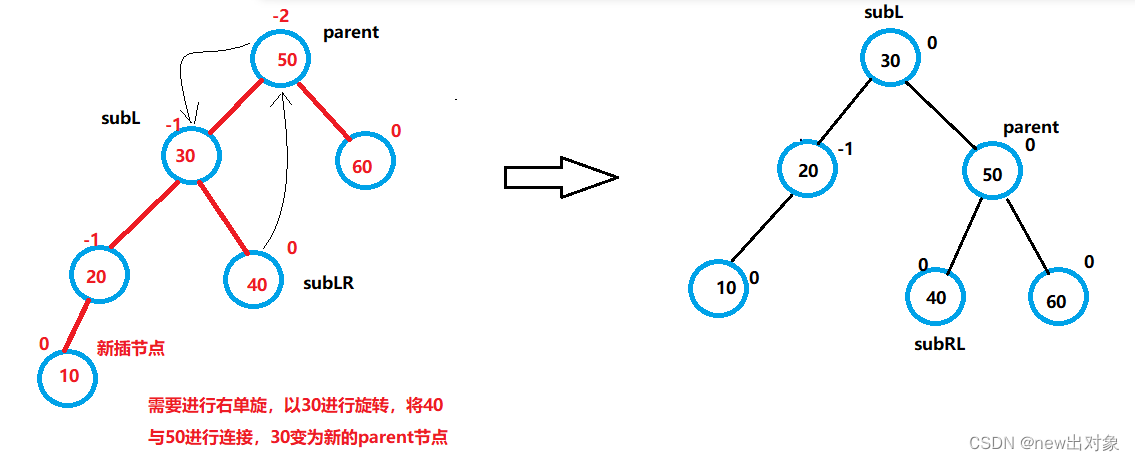 右旋代码： 

	void RotateR(Node* parent)
	{
		Node* subL = parent->_left;
		Node* subLR = subL->_right;
        
        //将subLR与parent相连接
		parent->_left = subLR;
		if (subLR)
		{
			subLR->_parent = parent;
		}
 
		Node* ppNode = parent->_parent;
        
        //subL变为新的parent节点
		subL->_right = parent;
		parent->_parent = subL;
 
        //将旋转后的子树与主树进行连接
		if (_root == parent)
		{
			_root = subL;
			subL->_parent = nullptr;
		}
		else
		{
			if (ppNode->_left == parent)
			{
				ppNode->_left = subL;
			}
			else
			{
				ppNode->_right = subL;
			}
 
			subL->_parent = ppNode;
		}
 
		subL->_bf = parent->_bf = 0;
	}

 3.左右双旋

旋转原因：

parent->bf == -2 && cur->bf == 1，在parent的左子树的右子树上进行插入，破坏了平衡因子。

需要先进行左旋，再进行右旋，再进行调整平衡因子。

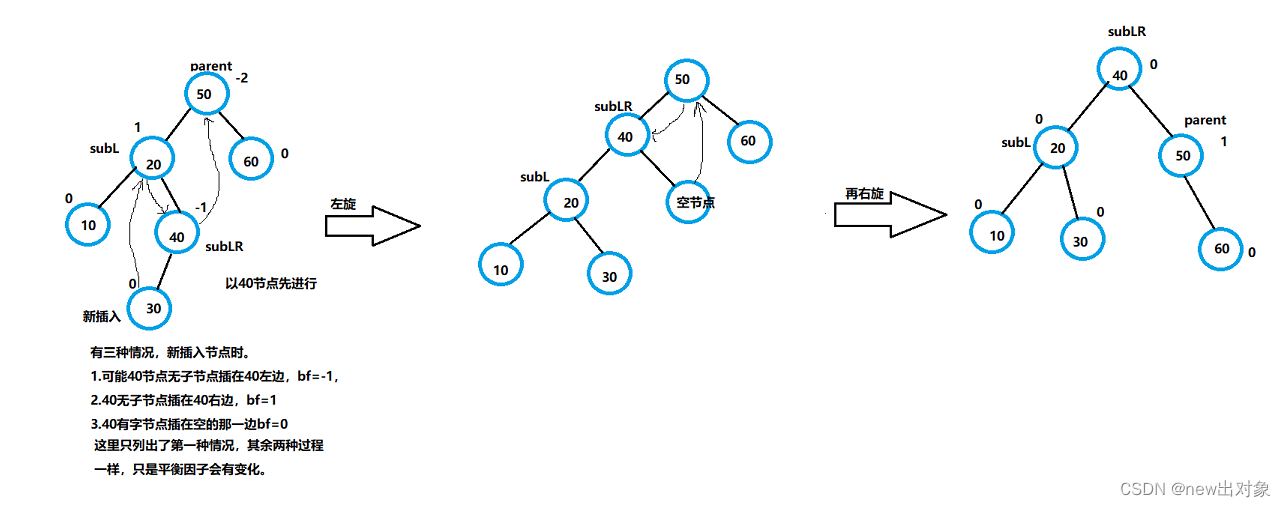
左右双旋代码 ：

	void RotateLR(Node* parent)
	{
		Node* subL = parent->_left;
		Node* subLR = subL->_right;
		int bf = subLR->_bf;
        
        //先左旋、再右旋，可以套用上面已实现的方法
		RotateL(parent->_left);
		RotateR(parent);
        subLR->_bf = 0;
        
        //调整平衡因子
        //有三种情况
		if (bf == 1)
		{
			parent->_bf = 0;
			subL->_bf = -1;
		}
		else if (bf == -1)
		{
			parent->_bf = 1;
			subL->_bf = 0;
		}
		else if (bf == 0)
		{
			parent->_bf = 0;
			subL->_bf = 0;
		}
		else
		{
			assert(false);
		}
	}

4.右左双旋

旋转原因：

parent->bf == 2 && cur->bf == -1。插入节点在右子树的左子树上

需要先进行右旋，再进行左旋，再调整平衡因子

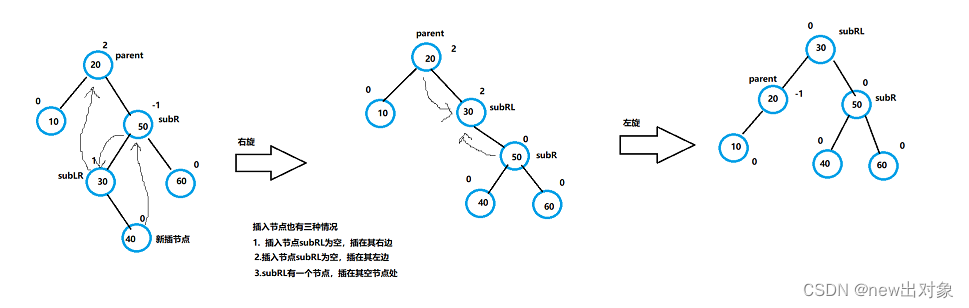 右左旋代码：

	void RotateRL(Node* parent)
	{
		Node* subR = parent->_right;
		Node* subRL = subR->_left;
 
		int bf = subRL->_bf;
 
        //先右旋，再左旋
		RotateR(parent->_right);
		RotateL(parent);
 
        //再调整平衡因子
		subRL->_bf = 0;
		if (bf == 1)
		{
			subR->_bf = 0;
			parent->_bf = -1;
		}
		else if (bf == -1)
		{
			subR->_bf = 1;
			parent->_bf = 0;
		}
		else if (bf == 0)
		{
			parent->_bf = 0;
			subR->_bf = 0;
		}
		else
		{
			assert(false);
		}
	}

 基于以上就是AVL树的概念和旋转的原理和代码的实现。