不正经

这个屌丝很懒，什么也没留下！

热门标签

复杂网络建模(一)_复杂网络模型

作者：不正经 | 2024-05-07 00:33:49

踩

复杂网络模型

1、复杂网络简介

网络在自然和人类社会中无处不在。在每个系统的背后都有一个网络，它定义了组件之间的交互。

从社交网络到万维网，网络以一种无处不在的方式来组织各种现实世界的信息。

1.1、图论基础

将人物抽象成节点，人物之间的关系抽象成连边。

网络科学源于图论，但不等同于图论。

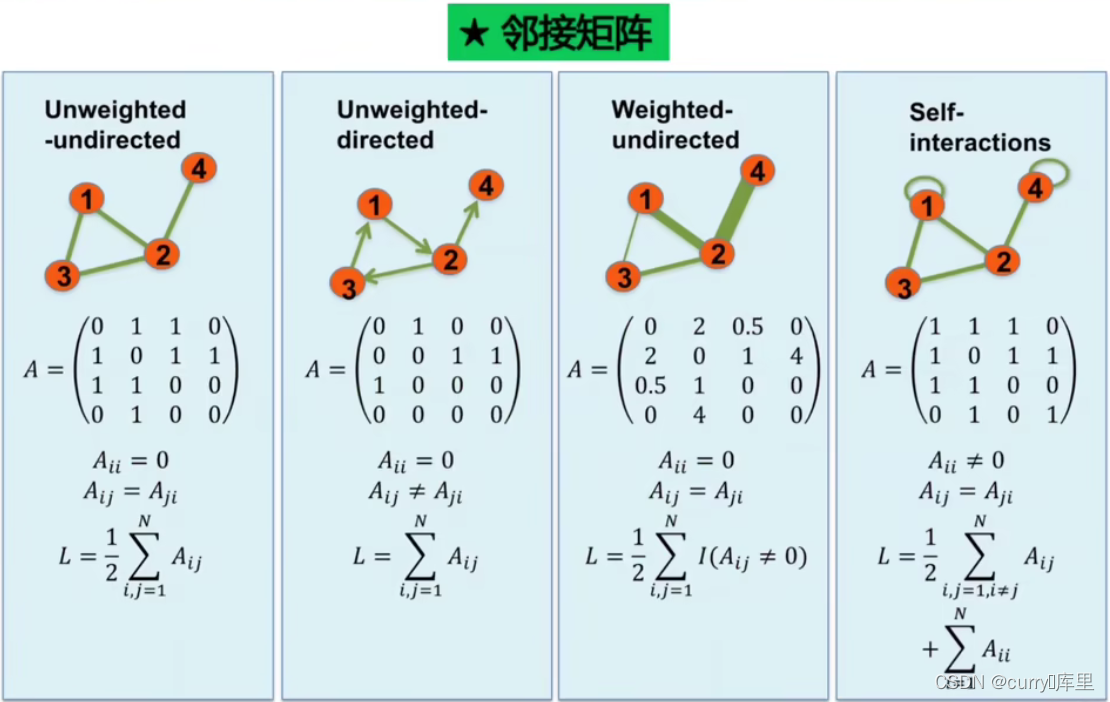
注意：L表示连边总个数

节点的度就是该节点的邻边数量。平均度就是所有节点的度的平均值。度分布描述了节点度的分布情况，通常可以用一个直方图来表示。

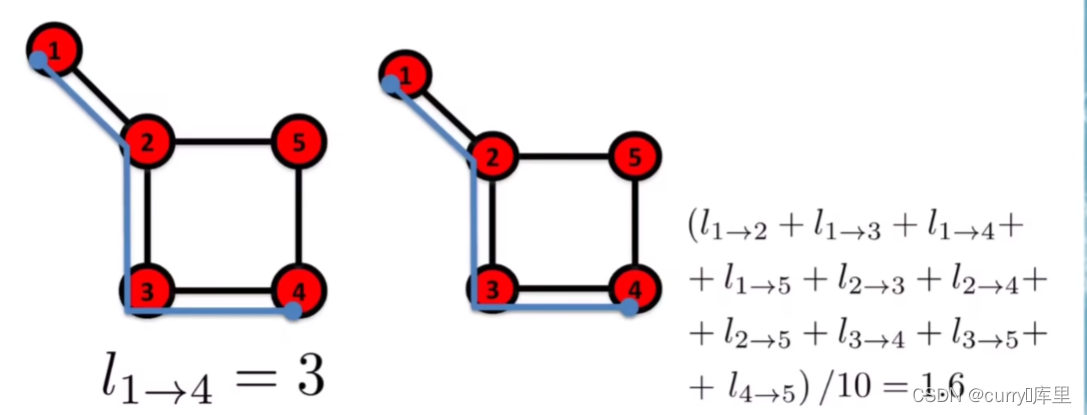
路径是沿着网络的连接运行的路由，路径的长度表示路径包含的连接数。在网络科学中，更多的是关注两个节点i和j之间的最短路径长度，最短路径长度通常被称为它们之间的距离。

在无向网络中，如果任意一对节点i和节点j之间至少存在一条路径，则网络是连通的；如果不存在路径，则网络是不连通的。

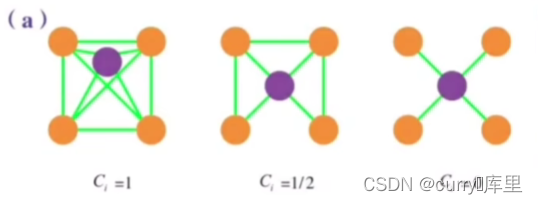
集聚系数用以捕获给定节点的邻居节点之间的连接程度。对于一个度为ki的节点i，局部集聚系数被定义为

注意：L是实际连边数，分母是最大的连边数。

整个网络的集聚程度可以由平均集聚系数所表征，它代表了所有节点的局部集聚系数的平均值。

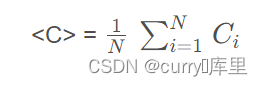
全局集聚系数

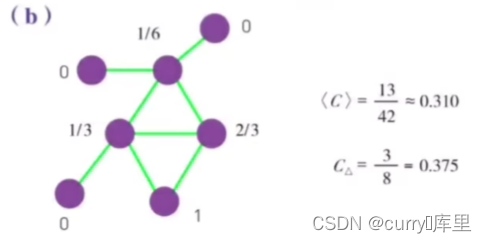
注意：全局集聚系数分母此题为6+6+3+1=16，分子为3*2.

2、网络的统计特征

2.1、网络的基本静态几何特征

2.1.1、度分布

大多数实际网络中的节点的度是满足一定的概率分布的。定义P(k)为网络中度为k的节点在整个网络中所占的比例。

规则网络：由于每个节点具有相同的度，所以其度分布集中在一个单一尖峰上，是一种Delta分布。

完全随机网络：度分布具有Poisson分布的形式，每一条边的出现概率是相等的，大多数节点的度是基本相同的，并接近于网络平均度<k>，远离峰值<k>，度分布则按指数形式急剧下降。把这类网络称为均匀网络。

无标度网络：具有幂指数形式的度分布： $P(k)\propto k^{-\gamma }$ 。所谓无标度是指一个概率分布函数 $F(x)$ 对于任意给定常数a存在常数b使得 $F(x)$ 满足 $F(ax)=bF(x)$ 。

幂律分布是唯一满足无标度条件的概率分布函数。许多实际大规模无标度网络，其幂指数通常为 $2\leqslant \gamma \leqslant 3$ ，绝大多数节点的度相对很低，也存在少量度值相对很高的节点（称为hub），把这类网络称为非均匀网络（异质网络）。

指数度分布网络： $P(k)\propto e^{-k/\kappa }$ ，式中 $\kappa >0$ 为一常数。

2.1.2、累计度分布

可以用累积度分布函数来描述度的分布情况，它与度分布的关系为

$P_{k}= \sum_{x=k}^{\infty}P(x)$

它表示度不小于k的节点的概率分布。

若度分布为幂律分布，即 $P(k)\propto k^{-\gamma }$ ，则相应的累计度分布函数符合幂指数为 $\gamma-1$ 的幂律分布

$P_{k}\propto \sum_{x=k}^{\infty }x^{-\gamma }\propto k^{-(\gamma -1)}$

若度分布为指数分布，即 $P(k)\propto e^{-k/\kappa }$ ，则相应的累积度分布函数符合同指数的指数分布

$P_{k}\propto \sum_{x=k}^{\infty }e^{-x/k}\propto e^{-k/\kappa }$

2.1.3、网络的直径和平均距离

网络中的两节点 $v_{i}$ 和 $v_{j}$ 之间经历边数最少的一条简单路径（经历的边各不相同），称为测地线。测地线的边数 $d_{ij}$ 称为两节点 $v_{i}$ 和 $v_{j}$ 之间的距离（或叫测地线距离）。

$1/d_{ij}$ 称为节点 $v_{i}$ 和 $v_{j}$ 之间的效率，记为 $\varepsilon _{ij}$ 。通常效率用来度量节点间的信息传递速度。当 $v_{i}$ 和 $v_{j}$ 之间没有路径连通时， $d_{ij} =\infty$ ，而 $\varepsilon _{ij} =0$ ，所以效率更适合度量非全连通网络。

网络的直径D定位为所有距离 $d_{ij}$ 中的最大值

$D = max_{1\leq i,j\leq N}d_{ij}$

平均距离（特征路径长度） $L$ 定义为所有节点对之间距离的平均值，它描述了网络中节点间的平均分离程度，即网络有多小，计算公式为

$L =\frac{1}{N^{2}}\sum_{j=1}^{N}\sum_{i=1}^{N}d_{ij}$

对于无向简单图来说， $d_{ij}$ = $d_{ij}$ 且 $d_{ii}$ =0，则上式可简化为

$L=\frac{2}{N(N-1)}\sum_{i=1}^{N}\sum_{j=i+1}^{N}d_{ij}$

很多实际网络虽然节点数巨大，但平均距离却小得惊人，这就是所谓的小世界效应。

2.1.4、集聚系数

集聚系数用以捕获给定节点的邻居节点之间的连接程度。节点的集聚系数定义为：设节点 $v_{i}$ 和 $k_{i}$ 个节点直接连接，那么对于无向网络来说，这 $k_{i}$ 个节点间可能存在的最大边数为 $k_{i}(k_{i}-1)/2$ ，而实际存在的边数为 $M_{i}$ ，由此我们定义 $C_{i}=2M_{i}/[k_{i}(k_{i}-1)]$ 为节点 $v_{i}$ 的集聚系数。

对于有向网络来说，这 $k_{i}$ 个节点间可能存在的最大弧数为 $k_{i}(k_{i}-1)$ ，此时 $v_{i}$ 的集聚系数 $C_{i}=M_{i}/[k_{i}(k_{i}-1)]$ 。

将该集聚系数对整个网络作平均，可得网络的平均集聚系数为 $<C>=\frac{1}{N}\sum_{i=1}^{N}C_{i}$

显然， $0\leq C\leq 1$ 。当 $C=0$ ，所以节点都是孤立节点，没有边连接。当 $C=1$ 时，网络为所有节点两两之间都有边连接的完全图。

2.1.5、度-度相关性

1.基于最近邻平均度值的度-度相关性

度-度相关性描述了网络中度大的节点和度小的节点之间的关系。若度大的节点倾向于和度大的节点连接，则网络是度-度正相关的；反之，若度大的节点倾向于和度小的节点连接，则网络是度-度负相关的。

节点 $v_{i}$ 的最近邻平均度值定义为

$k_{nn,i}=[\sum_{j}^{}a_{ij}k_{j}]/k_{i}$

式中， $k_{i}$ 表示节点 $v_{i}$ 的度值， $a_{ij}$ 为邻接矩阵元素。

所有度值为 $k$ 的节点的最近邻平均度值 $k_{nn}(k)$ 定义为

$k_{nn}(k)=\left ( \sum_{i,k_{i}=k}^{}k_{nn,i} \right )/\left [ N\cdot P(k) \right ]$

式中， $N$ 为节点总数， $P(k)$ 为度分布函数。

如果 $K_{nn}(k)$ 是随着 $k$ 上升的增函数，则说明度值大的节点倾向于和度值大的节点连接，网络具有正相关特性，称之为同配网络；反之网络具有负相关特性，称之为异配网络。

2.基于Pearson相关系数的度-度相关性

Newman利用两端节点的度Pearson相关系数 $r$ 来描述网络的度-度相关性，具体定义为 $r=\frac{{E^{-1}\sum_{e_{ij}}^{}k_{i}k_{j}-[E^{-1}\sum_{e_{ij}}^{}\frac{1}{2}(k_{i}+k_{j})]}^{2}}{{E^{-1}\sum_{e_{ij}}^{}\frac{1}{2}(k_{i}^{2}+k_{j}^{2})-[E^{-1}\sum_{e_{ij}}^{}\frac{1}{2}(k_{i}+k_{j})]}^{2}}$

式中， $k_{i},k_{j}$ 分别表示边 $e_{ij}$ 的两个节点 $v_{i},v_{j}$ 的度， $M$ 表示网络的总边数。

容易证明度-度相关系数 $r$ 的范围为： $0 \leq \left | r \right |\leq 1$ 。当 $r< 0$ 时，网络是负相关的；当 $r>0$ 时，网络是正相关的；当 $r=0$ 时，网络是不相关的。

2.1.5、介数和核度

1.介数

要衡量一个节点的重要性，其度值当然可以作为一个衡量指标，但又不尽然，例如在社会网络中，有的节点的度虽然很小，但它可能是两个社团的中间联络人，如果去掉该节点，那么就会导致两个社团的联系中断，因此该节点在网络中起到极其重要的的作用。对于这样的节点，需要定义另一种衡量指标，这就引出网络的另一重要的全局几何量——介数。

介数分为节点介数和边介数两种，反映了节点或边在整个网络中的作用和影响力。

节点的介数 $B_{i}$ 定义为

$B_{i}=\sum_{j\neq l\neq i}^{}[N_{jl}(i)/N_{jl}]$

式中， $N_{jl}$ 表示节点 $v_{j}$ 和 $v_{l}$ 之间的最短路径条数， $N_{jl}(i)$ 表示节点 $v_{j}$ 和 $v_{l}$ 之间的最短路径经过节点 $v_{i}$ 的条数。

边的介数 $B_{ij}$ 定义为

$B_{ij}=\sum_{(l,m)\neq (i,j)}^{}[N_{lm}(e_{ij})]/N_{lm}]$

式中， $N_{lm}$ 表示节点 $v_{l}$ 和 $v_{m}$ 之间的最短路径条数， $N_{lm}(e_{ij})$ 表示节点 $v_{l}$ 和 $v_{m}$ 之间的最短路径经过边 $e_{ij}$ 的条数。

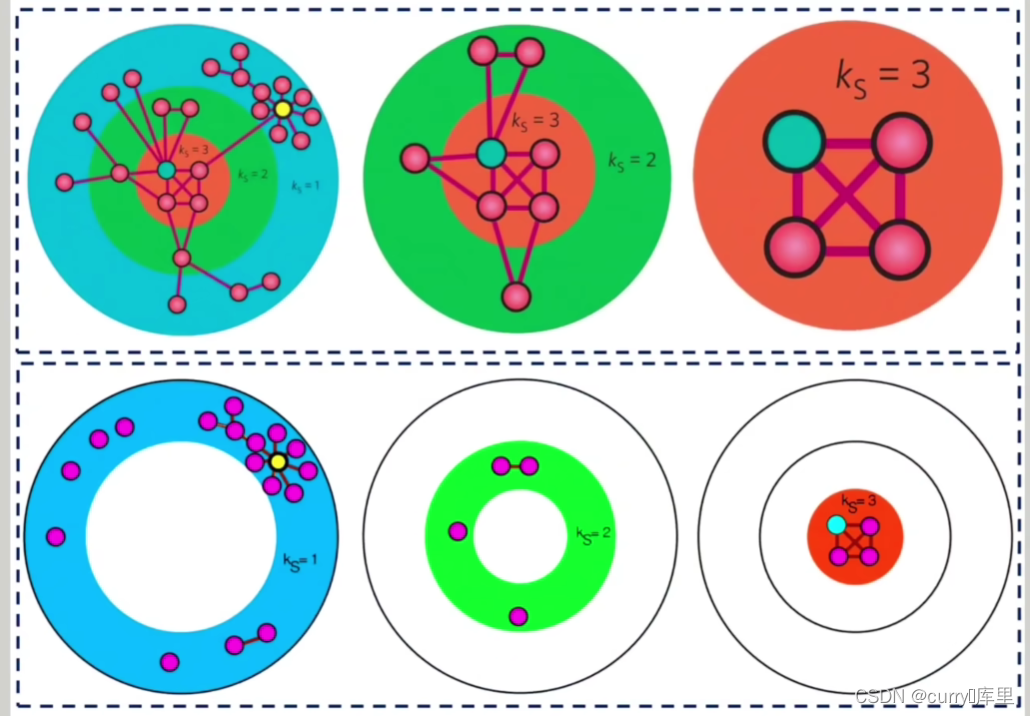
2.核度

一个图的k-核是指反复去掉度值小于k的节点及其连线后，所剩余的子图，该子图的节点数就是该核的大小。

若一个节点属于k-核，而不属于(k+1)-核，则此节点的核度为k。

节点核度的最大值叫做网络的核度。

节点的核度可以说明节点在核中的深度，核度的最大值自然就对应着网络结构中最中心的位置。k-核解析可用来描述度分布所不能描述的网络特征，揭示源于系统特殊结构的结构和层次性质。

2.1.7、网络密度

网络密度指的是一个网络中各节点之间联络的紧密程度。网络G的网络密度 $d(G)$ 定义为

$d(G)=2M/[N(N-1)]$

式中， $M$ 为网络中实际拥有的连接数， $N$ 为网络节点数。

网络密度的取值范围为 $[0,1]$ ，当网络内部完全连通时，网络密度为1，而实际网络的密度通常远小于1，实际网络中能够发现的最大密度值是0.5。

2.2、几种常用的中心性指标

1.度中心性

度中心性分为节点度中心性和网络度中心性。前者指的是节点在其与之直接相连的邻居节点当中的中心程度，而后者则侧重节点在整个网络的中心程度，表征的是整个网络的集中或集权程度，即整个网络围绕一个节点或一组节点来组织运行的程度。

节点 $v_{i}$ 的度中心性 $C_{D}(v_{i})$ 定义为

$C_{D}(v_{i})=k_{i}/(N-1)$

2.介数中心性

介数中心性分为节点介数中心性和网络介数中心性。

节点 $v_{i}$ 的介数中心性 $C_{B}(v_{i})$ 定义为

$C_{B}(v_{i})=2B_{i}/[(N-2)(N-1)]$

与度中心性类似，可得到 $H=N-1$ （也是星型网络，中心节点的介数中心性为1，其它节点的介数中心性为0）。

3.接近度中心性

对于连通图来说，节点 $v_{i}$ 的接近度中心性 $C_{C}(v_{i})$ 定义为

$C_{C}(v_{i})=(N-1)/[\sum_{j=1,j\neq i}^{N}d_{ij}]$

4.特征向量中心性

$Ax=\lambda x$

通常，上式的各个特征向量对应不同的特征值 $\lambda$ 。在这里，一个额外的要求是特征向量的每个分量必须是正数。根据Perron-Frobenius定理，只有最大的特征值对应的特征向量才是中心性测度所需要的。求这个特征向量可采用幂迭代算法。在最后得到的特征向量中，第 $i$ 个分量 $x_{i}$ 就是节点 $v_{i}$ 的特征向量中心性 $C_{E}(v_{i})$ 。

2.3、有向网络与加权网络的静态特征

2.3.1、有向网络的静态特征

1.入度和出度

由于与有向网络某个节点相关联的弧有指向节点的，也有背向节点向外的，因此除了可以统计与某个节点相关联的弧数，也就是度之外，有必要分开统计两个方向的弧数，分别称为节点的入度和出度。

节点 $v_{i}$ 的入度、出度和有向图的邻接矩阵以及度的关系为

$k_{i}^{in} =\sum_{j=1}^{N}a_{ji}$ 、 $k_{i}^{out} =\sum_{j=1}^{N}a_{ij}$ 、 $k_{i}=k_{i}^{out}+k_{i}^{in}$

同平均度一样，也可以求平均入度 $<k^{in}>$ 和平均出度 $<k^{out}>$ 为

$<k^{in}>=\sum_{i=1}^{N}k_{i}^{in}/N$ 、 $<k^{out}>=\sum_{i=1}^{N}k_{i}^{out}/N$

2.入度分布和出度分布

入度分布和出度分布分别记为 $P_{in}(k)$ 和 $P_{out}(k)$ ，分别表示网络中任意取出一个节点，其入度值和出度值刚好为 $k$ 的概率。

入（出）度分布与平均入（出）度之间具有如下关系式

$<k^{in}>=\sum_{k=0}^{k_{max}^{i}}kP_{in}(k)$ 、 $<k^{out}>=\sum_{k=0}^{k_{max}^{o}}kP_{out}(k)$

3.累积入度分布和累积出度分布

累积入（出）度分布与入（出）度分布的关系为

$P_{k}^{in}=\sum_{x=k}^{\infty }P_{in}(x)$ 、 $P_{k}^{out}=\sum_{x=k}^{\infty }P_{out}(x)$

容易证明入（出）度幂律分布对应的累积分布也是幂律分布，入（出度指数分布对应的累积分布也是同指数的指数分布。）

4.平均距离和效率

由于有向网络里的弧是带有方向的，所以从节点 $v_{i}$ 到 $v_{j}$ 之间的距离 $d_{ij}$ 和从节点 $v_{j}$ 到 $v_{i}$

之间的距离 $d_{ji}$ 是不同的。距离 $d_{ij}$ 定义为从节点 $v_{i}$ 出发沿着同一方向到达节点 $v_{j}$ 所要经历的弧的最少数目，而它的倒数 $1/d_{ij}$ 称为从节点 $v_{i}$ 到 $v_{j}$ 的效率，记为 $\varepsilon_{ij}$ 。

有向连通简单网络的平均距离 $L$ 定义为所有节点对之间距离的平均值，定义为

$L=\frac{1}{N(N-1)}\sum_{i\neq j}^{}d_{ij}$

因为效率可以用来描述非连通网络，所以可以定义为有向网络的效率 $L_{C}$ 为

$L=\frac{1}{N(N-1)}\sum_{i\neq j}^{}\varepsilon_{ij}$

2.3.2、加权网络的静态特征

1.点权：节点 $v_{i}$ 的点权 $S_{i}$ 定义为 $S_{i}=\sum_{j\in N_{i}}^{}w_{ij}$

式中， $N_{i}$ 表示节点 $v_{i}$ 的邻点集合， $w_{ij}$ 表示连接节点 $v_{i}$ 和节点 $v_{j}$ 的边的权重。

2.单位权：节点 $v_{i}$ 的单位权 $U_{i}$ 定义为 $U_{i}=S_{i}/k_{i}$

3.基于节点的权-度相关性：对于单个节点来说，其点权和其度之间的相关性

$\bar{s}(k)=(\sum_{i:k_{i}=k}^{}s_{i})/[N\cdot P(k)]$ ，它表示所有节点为 $k$ 的节点的点权的平均值。

4.基于边的权-度相关性

5.权重分布的差异性

节点 $v_{i}$ 的权重分布差异性 $Y_{i}$ 表示与节点 $v_{i}$ 相连的边权分布的离散程度，定义为

$Y_{i}=\sum_{j\in N_{i}}^{}(w_{ij}/s_{i})^{2}$

差异性与度有如下关系：如果与节点 $v_{i}$ 相关联的边的权重值差别不大，则 $Y_{i}\propto 1/k_{i}$ ；如果权值相差较大，例如只有一条边的权重起主要作用，则 $Y_{i}\approx 1$ 。所有节点度为 $k$ 的权重分布差异性的平均值被定义为

$\bar{Y}(k)=\frac{(\sum_{i|k_{i}=k}^{}Y_{i})}{[N\cdot P(k)]}$

三、复杂网络的发展

经典复杂网络模型

网络科学理论发展的三个时期：

规则网络：1736，欧拉（Euler）--- 图论之父
随机网络：1959，Erdos和Renyi建立了著名的随即图理论
复杂网络：1988年Watts和Strogatz提出了小世界网络模型；1999年Barabasi等人提出了BA无标度网络模型。

3.1、规则（Regular）网络

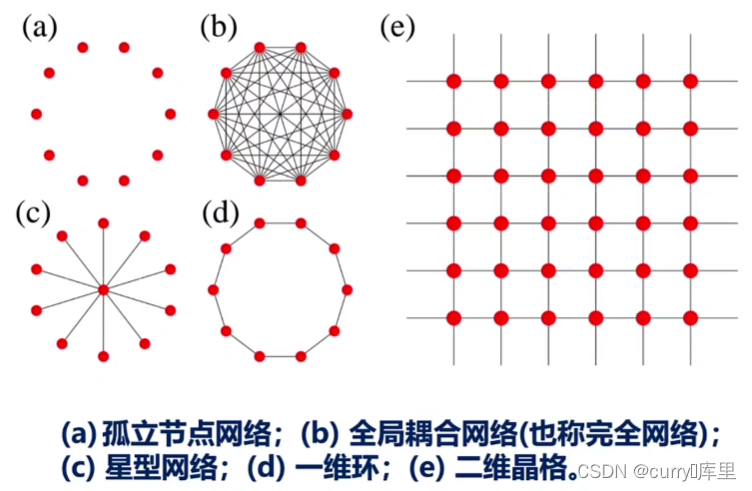
(a)(c)(d)(e)四个网络的集聚系数均为0，(b)的集聚系数为1；以及直径：完全网络的直径为1，一维环状网络的直径为节点数N的一半，二维晶格的直径为L等等。

3.2、ER随机网络的生成算法

随机网络的两种生成方式：

（1）G(N,L)模型

N个节点通过L条随机放置的链接彼此相连。埃尔德什和雷尼在他们关于随机网络的系列论文中采用的是这种定义方式。（平均度： $<k>\approx \frac{2L}{N}$ ）

（2）G(N,p)模型

N个节点中，每对节点之间以概率p彼此相连。

构建随机网络G(N,p)模型的步骤如下：

从N个孤立节点开始。
选择一对节点，产生一个0到1之间的随机数。如果该随机数小于p，在这对节点之间放置一条链接；否则，该节点对保持不连接。
对所有N(N-1)/2个节点对，重复步骤2。

3.3、ER随机网络结构特性

3.3.1、期望连边数

随机网络恰好有 $L$ 条链接的概率，是如下三项的乘积：

（1） $L$ 个点对之间存在链接的概率，即 $pL$ 。

（2）剩余 $N(N-1)/2-L$ 个点对之间没有链接的概率，即 $(1-p)N(N-1)/2-L$ 。

（3）在所有 $N(N-1)/2$ 个点对选择 $L$ 个点对放置链接，所有可能选择方式数为：

排列组合的方式 $\begin{pmatrix} N(N-1)/2\\ L \end{pmatrix}$

因此，随机网络恰好有 $L$ 条链接的概率为： $p_{L}=\begin{pmatrix} N(N-1)/2\\ L \end{pmatrix}p^{L}(1-p)^{\frac{N(N-1)}{2}-L}$

上式是一个二项式分布，因此随机网络的期望链接数为：

$<L>=\sum_{L=0}^{\frac{N(N-1)}{2}}Lp_{L}=p\frac{N(N-1)}{2}$ $k$

在连接概率为 $p$ 的ER随机图中，可知其平均度为 $<k>=\frac{2<L>}{N}=p(N-1)\approx pN$

3.3.2、二项分布

随机网络中，一个节点 $i$ 恰好有 $k$ 个链接的概率是下面三项的乘积：

（1） $k$ 个链接出现的概率，即 $pk$ 。

（2）剩下 $(N-1-k)$ 个链接不出现的概率，即 $(1-p)N-1-k$ 。

（3）节点 $i$ 的 $N-1$ 个可能存在的链接中选出 $k$ 个，选择方式的总数为：

$\begin{pmatrix} N-1\\ k \end{pmatrix}$

因此，随机网络的度分布服从二项分布：

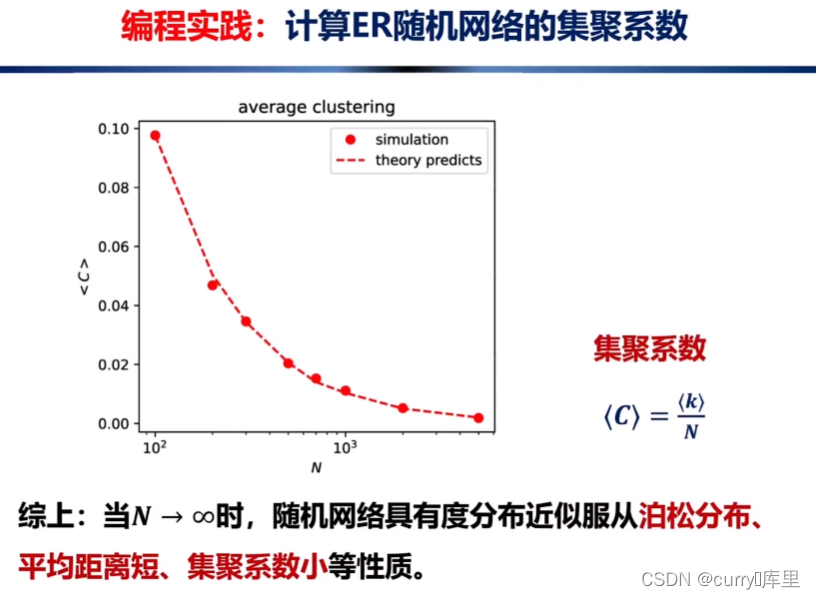
$p_{k}=\begin{pmatrix} N-1\\ k \end{pmatrix}p^{k}(1-p)^{N-1-k}$

随机网络度分布的精确形式是二项分布。当 $N\gg <k>$ 时，二项分布可以很好地近似为泊松分布。

3.3.3、泊松分布

大部分真实网络是稀疏的，意味着这些网络的平均度远小于网络大小。极限情况下，二项分布可以近似为如下泊松分布

$p_{k}=e^{-<k>}\frac{<k>^{k}}{k!}$

上式通常被称为随机网络的度分布。

声明：本文内容由网友自发贡献，转载请注明出处：【wpsshop】